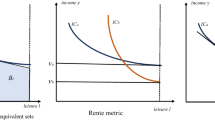
Abstract
This paper explores how to rank social allocations when individuals have other-regarding preferences (ORPs). Unlike the few existing studies on this issue, we focus on two different private goods, only one of which generates ORPs concerns. Specifically, individuals exhibit other-regarding views about the social health state but have standard self-centered preferences over other goods, namely consumption. Our social evaluation also incorporates a fairness view that aims to reduce inequalities that originate from factors for which individuals should not be deemed responsible. By resorting to a non-resourcist approach, we derive social preferences that seek to reduce individual well-being inequalities. Such differences are assessed by means of an interpersonal comparable measure that is related to an ideal situation which involves neither externalities nor unfair inequalities. We obtain that the use of the state of perfect health as the reference value leads society to give a higher priority to those who exhibit more altruistic preferences.


Similar content being viewed by others
Notes
Winkelmann and Winkelmann (1995) and Mendolia (2014) obtain similar subjective well-being losses for the case of partner’s unemployment, and moreover that they clearly exceed the pecuniary losses. These authors also argue that such a gender asymmetry shows the traditional role distribution within the household.
A similar way of introducing relative views in a framework in which consumption is the only good in the economy is presented by Treibich (2019).
Although different, this property bears some resemblance to the principles that impose well-being lower and upper bounds (e.g., Maniquet and Sprumont 2005).
The \(\lambda \)-relative equivalent for such agents would be a positive value that may go to \(+\infty \).
Where \(Z^{n}(h^{*})\) denotes the set of allocations in which \(h_{i}=h^{*}\) for all \(i\in N\). These allocations can always be constructed since any individual’s level of health, that is \(h^{*}\), cannot be larger than the aggregate state in society.
References
Bauer M, Chytilová J, Pertold-Gebicka B (2014) Parental background and other-regarding preferences in children. Exp Econ 17(1):24–46
Bossert W, Fleurbaey M, Van de Gaer D (1999) Responsibility, talent, and compensation: a second-best analysis. Rev Econ Des 4(1):35–55
Braakmann N (2014) The consequences of own and spousal disability on labor market outcomes and subjective well-being: evidence from germany. Rev Econ Househ 12(4):717–736
Bruhin A, Winkelmann R (2009) Happiness functions with preference interdependence and heterogeneity: the case of altruism within the family. J Popul Econ 22(4):1063–1080
Calo-Blanco A (2016) Fair compensation with different social concerns for forgiveness. Rev Econ Des 20(1):39–56
Carrieri V (2012) Social comparison and subjective well-being: Does the health of others matter? Bull Econ Res 64(1):31–55
Clark AE, Frijters P, Shields MA (2008) Relative income, happiness, and utility: an explanation for the easterlin paradox and other puzzles. J Econ Liter 46(1):95–144
D’Aspremont C, Gevers L (1977) Equity and the informational basis of collective choice. Rev Econ Stud 44(2):199–209
De Mello L, Tiongson ER (2009) What is the value of (my and my family’s) good health? Kyklos 62(4):594–610
Decerf B, Van der Linden M (2016) Fair social orderings with other-regarding preferences. Social Choice Welfare 46(3):655–694
Dickie M, Messman VL (2004) Parental altruism and the value of avoiding acute illness: Are kids worth more than parents? J Environ Econ Manag 48(3):1146–1174
Dufwenberg M, Heidhues P, Kirchsteiger G, Riedel F, Sobel J (2011) Other-regarding preferences in general equilibrium. Rev Econ Stud 78(2):613–639
Fehr E, Schmidt K M (2006) The economics of fairness, reciprocity and altruism—experimental evidence and new theories. In: Kolm S-C, Ythier JM (Eds), Foundations, vol 1. Handbook of the economics of giving, altruism and reciprocity, Chap. 8. Elsevier, pp 615–691
Fleurbaey M (2005a) Health, wealth, and fairness. J Public Econ Theory 7(2):253–284
Fleurbaey M (2005b) The Pazner-Schmeidler social ordering: a defense. Rev Econ Des 9(2):145–166
Fleurbaey M (2012) The importance of what people care about. Polit Philos Econ 11(4):415–447
Fleurbaey M, Maniquet F (2005) Fair social orderings when agents have unequal production skills. Social Choice Welfare 24(1):93–127
Fleurbaey M, Maniquet F (2011) A theory of fairness and social welfare. Cambridge University Press, Cambridge
Fleurbaey M, Schokkaert E (2011) Equity in health and health care. In: Pauly MV, Mcguire TG, Barros PP (eds) Handbook of Health Economics, Vol 2, Chap 16. Elsevier, pp 1003–1092
Forssén ASK, Carlstedt G, Mörtberg CM (2005) Compulsive sensitivity-a consequence of caring: a qualitative investigation into women carer’s difficulties in limiting their labours. Health Care Women Int 26(8):652–671
Frank RH (2005) Positional externalities cause large and preventable welfare losses. Am Econ Rev 95(2):137–141
Golics CJ, Basra MKA, Finlay AY, Salek S (2013) The impact of disease on family members: a critical aspect of medical care. J R Soc Med 106(10):399–407
Hammond PJ (1976) Equity, Arrow’s conditions, and Rawls’ difference principle. Econometrica 44(4):793–804
Harsanyi JC (1982) Morality and the theory of rational behaviour. In: Sen A, Williams B (eds) Utilitarianism and beyond. Cambridge University Press, Cambridge, pp 39–62
Hougaard JL, Moreno-Ternero JD, Østerdal LP (2013) A new axiomatic approach to the evaluation of population health. J Health Econ 32(3):515–523
Luttmer EFP (2005) Neighbors as negatives: relative earnings and well-being. Q J Econ 120(3):963–1002
Maniquet F, Sprumont Y (2005) Welfare egalitarianism in non-rival environments. J Econ Theory 120(2):155–174
Mendolia S (2014) The impact of husband’s job loss on partners’ mental health. Rev Econ Househ 12(2):277–294
Østerdal LP (2005) Axioms for health care resource allocation. J Health Econ 24(4):679–702
Pazner EA, Schmeidler D (1978) Egalitarian equivalent allocations: A new concept of economic equity. The Quarterly Journal of Economics 92(4):671–687
Pinquart M, Sörensen S (2006) Gender differences in caregiver stressors, social resources, and health: an updated meta-analysis. J Gerontol Ser B 61(1):33–45
Post SG (2007) Altruism and health: perspectives from empirical research. Oxford University Press, Oxford
Rees J, O’Boyle C, MacDonagh R (2001) Quality of life: impact of chronic illness on the partner. J R Soc Med 94(11):563–566
Sobel J (2005) Interdependent preferences and reciprocity. J Econ Liter 43(2):392–436
Treibich R (2019) Welfare egalitarianism with other-regarding preferences. Social Choice Welfare 52(1):1–28
Ussher JM, Sandoval M (2008) Gender differences in the construction and experience of cancer care: the consequences of the gendered positioning of carers. Psychol Health 23(8):945–963
Viscusi WK, Magat WA, Forrest A (1988) Altruistic and private valuations of risk reduction. J Policy Anal Manag 7(2):227–245
Winkelmann L, Winkelmann R (1995) Happiness and unemployment: a panel data analysis for germany. Appl Econ Q 41(4):293–307
Yee JL, Schulz R (2000) Gender differences in psychiatric morbidity among family caregivers: a review and analysis. The Gerontologist 40(2):147–164
Acknowledgements
I would like to thank Rafael Treibich, Mar Calo and the participants to seminars and conferences in Seville, Odense, Bilbao and Alicante for their comments. Financial support from the Spanish Ministry of Economy and Competitiveness (ECO2017-83069-P and ECO2014-57413-P) is gratefully acknowledged. The usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Proposition 1
For any \(e\in {\mathcal {E}}\), let us assume an allocation \(z_{N}\in Z^{n}\). Because of Consumption Desirability, each individual \(i\in N\) prefers a strictly positive level of consumption than no consumption at all, whatever the others’ situation is. Therefore, \(((h_{i},c),\overline{h}_{z})P_{i}\left( (h^{*},0),h^{*}\right) \) for any \(c>0\). Hence, due to monotonicity in one’s own consumption \(\lambda _{i}(z_{N})\) cannot be negative.
As regards the existence of \(\lambda _{i}(z_{N})\), because of continuity, monotonicity and the previous result there exists \(\widehat{\lambda }\in {\mathbb {R}}_{+}\) such that for all \(\lambda \le \widehat{\lambda }\) we have that \(z_{N}R_{i}\left( (h^{*},\lambda c^{*}_{e}(\widehat{R}_{i})),h^{*} \right) \). Moreover, because of Altruism, monotonicity and the choice of \(h^{*}\) as the reference value it is always possible to find \(\widetilde{\lambda }\in {\mathbb {R}}_{++}\) such that \(\left( (h^{*},\lambda c^{*}_{e}(\widehat{R}_{i})),h^{*} \right) R_{i}z_{N}\) for all \(\lambda \ge \widetilde{\lambda }\). Since both \(\widehat{\lambda }\) and \(\widetilde{\lambda }\) exist for any \(i\in N\), and given that \({\mathbb {R}}_{+}\) is a connected space, by continuity there exits \(\lambda _{i}(z_{N})\in {\mathbb {R}}_{+}\) such that \(z_{N}I_{i}\left( (h^{*},\lambda _{i}(z_{N})c^{*}_{e}(\widehat{R}_{i})),h^{*} \right) \).
Finally, let us assume that for some individual \(i\in N\) there exist \(\lambda _{i}(z_{N}),\lambda '_{i}(z_{N})\in {\mathbb {R}}_{+}\) such that \(\lambda _{i}(z_{N})>\lambda '_{i}(z_{N})\). Because of monotonicity in one’s own consumption \(\left( (h^{*},\lambda _{i}(z_{N})c^{*}_{e}(\widehat{R}_{i})),h^{*} \right) P_{i} \left( (h^{*},\lambda '_{i}(z_{N})c^{*}_{e}(\widehat{R}_{i})),h^{*} \right) \). Therefore, the individual is not indifferent between these two allocations, and hence \(\lambda _{i}(z_{N})\) and \(\lambda '_{i}(z_{N})\) cannot both at the same time represent her preferences over the allocation \(z_{N}\in Z^{n}\).
Consequently, the \(\lambda \)-relative equivalent \(\lambda _{i}(z_{N})\) is well-defined for all agents, that is, this value exists and it is positive and unique.
1.2 Proof of Theorem 1
The proof of Theorem 1 is based on the characterisation of the leximin criterion proposed by Hammond (1976), and it is split in four steps. The version of the proof that we present here relies on the assumption that the population can vary.
Step 1: Indifference of \({\mathbf{R }}^{\lambda }_{\mathrm{lex}}\) For any economy \(e\in {\mathcal {E}}\), let us assume two allocations \(z_{N},z'_{N}\in Z^{n}\) and two individuals \(j,k\in N\) such that, without loss of generality, \(\lambda _{k}(z'_{N})=\lambda _{j}(z_{N})<\lambda _{k}(z_{N})=\lambda _{j}(z'_{N})<1\), and \(\lambda _{i}(z_{N})=\lambda _{i}(z'_{N})\) for all \(i\ne j,k\). When the values of the \(\lambda \)-relative equivalents are different to the ones proposed here the same proof can be induced by means of Perfect Consumption Scale Independence. We will show that under such conditions \(z_{N}\mathbf{I }(e)z'_{N}\). Opposite to the desired result, let us assume that \(z_{N}\mathbf{P }(e)z'_{N}\).
Due to the properties of the ORPs it is possible to define two perfect health allocations \(\widehat{z}_{N},\widehat{z}'_{N}\in Z^{n}(h^{*})\)Footnote 6 such that for all \(i\in N\):
Note that since \(\lambda _{i}(z_{N})\) is a valid measure of the individual well-being, one has that \(\widehat{z}_{i}=\widehat{z}'_{i}\) for all \(i\ne j,k\). Hence, if we apply Strong Pareto (which implies Pareto Indifference) we have that \(\widehat{z}_{N}\mathbf{P }(e)\widehat{z}'_{N}\).
Let us now introduce two additional individuals a and b such that \(R_{a}=R_{j}\in {\mathcal {R}}\) and \(R_{b}=R_{k}\in {\mathcal {R}}\). Let us also assume, with \(\beta >1\), the following levels of consumption (see Fig. 3a):
Proof of Theorem 1
According to the assumption \(z_{N}\mathbf{P }(e)z'_{N}\), by Strong Pareto and Consistency we obtain that \((\widehat{z}_{N},(h^{*},c_{a}),(h^{*},c_{b}))\mathbf{P }(e)(\widehat{z}'_{N},(h^{*},c_{a}),(h^{*},c_{b}))\). By Priority Among Equals twice we obtain the social relation \((\widehat{z}'_{N},(h^{*},c'_{a}),(h^{*},c'_{b}))\mathbf{I }(e)(\widehat{z}_{N},(h^{*},c_{a}),(h^{*},c_{b}))\). By Transitivity and Consistency \(((h^{*},c'_{a}),(h^{*},c'_{b}))\mathbf{P }(e)((h^{*},c_{a}),(h^{*},c_{b}))\). Finally, by Perfect Consumption Scale Independence we conclude that \(((h^{*},c'''_{a}),(h^{*},c'''_{b}))\mathbf{P }(e)((h^{*},c''_{a}),(h^{*},c''_{b}))\). However, using Well-being Bound Transfer we obtain that \(((h^{*},c''_{a}),(h^{*},c''_{b}))\mathbf{I }(e)((h^{*},c'''_{a}),(h^{*},c'''_{b}))\), which yields the desired contradiction.
Step 2: Strict preference of \({\mathbf{R }}^{\lambda }_{\mathrm{lex}}\) For any \(e\in {\mathcal {E}}\), let us assume two allocations \(z_{N},z'_{N}\in Z^{n}\) and two individuals \(j,k\in N\) such that, without loss of generality, \(\lambda _{j}(z'_{N})<\lambda _{k}(z_{N})<\lambda _{j}(z_{N})<\lambda _{k}(z'_{N})\), and \(\lambda _{i}(z_{N})=\lambda _{i}(z'_{N})\) for all \(i\ne j,k\). First, we need to prove that it must be the case that \(z_{N}\mathbf{P }(e)z'_{N}\). Opposite to the desired result, let us assume that \(z'_{N}\mathbf{R }(e)z_{N}\).
Due to the basic axioms of the ORPs it is possible to define two perfect health allocations \(\widehat{z}_{N},\widehat{z}'_{N}\in Z^{n}(h^{*})\) such that for all \(i\in N\):
Once again, \(\widehat{z}_{i}=\widehat{z}'_{i}\) for all \(i\ne j,k\), and hence \(\widehat{z}'_{N}\mathbf{R }(e)\widehat{z}_{N}\) by Strong Pareto.
To obtain our result we distinguish between two possible scenarios according to the value of \(\lambda _{j}(z'_{N})\). We first assume \(\lambda _{j}(z'_{N})<1\). Let us introduce two individuals a and b with ORPs \(R_{a}=R_{j}\) and \(R_{b}=R_{k}\). Let us also assume, with \(\beta ,\varepsilon \in {\mathbb {R}}_{++}\), the following levels of consumption:
Because of continuity and Perfect Consumption Scale Independence, such bundles can always be found (see Fig. 3b). Given the initial assumption \(z_{N}\mathbf{R }(e)z'_{N}\), by Strong Pareto \(\widehat{z}'_{N}\mathbf{R }(e)\widehat{z}_{N}\). By Perfect Consumption Scale Independence \(((h^{*},\beta \widehat{c}'_{i})_{i\ne j,k},(h^{*},c''_{j})\), \((h^{*},c''_{k}))\mathbf{R }(e)((h^{*},\beta \widehat{c}_{i})_{i\in N\setminus \{j,k\}},(h^{*},c'''_{j}),(h^{*},c'''_{k}))\). By Consistency it is straightforward to check that \(((h^{*},c''_{j}),(h^{*},c''_{k}),(h^{*},c_{a}),(h^{*},c_{b}))\) \(\mathbf{R }(e)((h^{*},c'''_{j}),(h^{*},c'''_{k}),(h^{*},c_{a}),(h^{*},c_{b}))\). If we apply Priority Among Equals twice we have \(((h^{*},c''''_{j}),(h^{*},c'''_{k}),(h^{*},c'_{a}),(h^{*},c'_{b}))\) \(\mathbf{R }(e)((h^{*},c''_{j}),(h^{*},c''_{k}),(h^{*},c_{a}),(h^{*},c_{b}))\). By Strong Pareto we obtain that \(((h^{*},c'''_{j}),(h^{*},c'''_{k}),(h^{*},c'_{a}),(h^{*},c'_{b}))\) \(\mathbf{P }(e)((h^{*},c''''_{j}),(h^{*},c'''_{k}),(h^{*},c'_{a}),(h^{*},c'_{b}))\). Finally, by Transitivity \(((h^{*},c'''_{j}),(h^{*},c'''_{k}),(h^{*},c'_{a}),(h^{*},c'_{b}))\) \(\mathbf{P }(e)((h^{*},c'''_{j}),(h^{*},c'''_{k}),(h^{*},c_{a}),(h^{*},c_{b}))\). However, by Well-being Bound Transfer axiom we obtain that \(((h^{*},c'''_{j}),(h^{*},c'''_{k}),(h^{*},c_{a}),(h^{*},c_{b})\) \(\mathbf{R }(e)((h^{*},c'''_{j}),(h^{*},c'''_{k}),(h^{*},c'_{a}),(h^{*},c'_{b}))\), which yields the desired contradiction.
Let us now derive a similar contradiction for \(\lambda _{j}(z'_{N})\ge 1\). To do so we assume, once again, two individuals a and b with ORPs \(R_{a}=R_{j}\) and \(R_{b}=R_{k}\). Let us also assume, with \(\beta ,\varepsilon \in {\mathbb {R}}_{++}\), the following levels of consumption:
One again, by Strong Pareto \(\widehat{z}'_{N}\mathbf{R }(e)\widehat{z}_{N}\). By Consistency \(((h^{*},\widehat{c}'_{j}),(h^{*},\widehat{c}'_{k}),(h^{*},c''_{a}),(h^{*},c''_{b}))\) \(\mathbf{R }(e)((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}_{k}),(h^{*},c''_{a}),(h^{*},c''_{b}))\). By Priority Among Equals we obtain that \(((h^{*},c''_{j}),(h^{*},\widehat{c}'_{k}),(h^{*},c'''_{a}),(h^{*},c''_{b}))\) \(\mathbf{R }(e)((h^{*},\widehat{c}'_{j}),(h^{*},\widehat{c}'_{k}),(h^{*},c''_{a}),(h^{*},c''_{b}))\), and moreover by Strong Pareto we also have \(((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}'_{k}),(h^{*},c'''_{a}),(h^{*},c''_{b}))\) \(\mathbf{P }(e)((h^{*},c''_{j}),(h^{*},\widehat{c}'_{k}),(h^{*},c'''_{a}),(h^{*},c''_{b}))\). Applying Priority Among Equals once more we obtain that \(((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}_{k}),(h^{*},c'''_{a}),(h^{*},c'''_{b}))\) \(\mathbf{R }(e)((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}'_{k}),(h^{*},c'''_{a}),(h^{*},c''_{b}))\). Finally, by Transitivity \(((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}_{k}),(h^{*},c'''_{a}),(h^{*},c'''_{b}))\) \(\mathbf{P }(e)((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}_{k}),(h^{*},c''_{a}),(h^{*},c''_{b}))\). However, by Well-being Bound Transfer axiom we obtain that \(((h^{*},c_{a}),(h^{*},c_{b}))\mathbf{R }(e)((h^{*},c'_{a}),(h^{*},c'_{b}))\), which by Perfect Consumption Scale Independence leads to \(((h^{*},c''_{a}),(h^{*},c''_{b}))\mathbf{R }(e)((h^{*},c'''_{a}),(h^{*},c'''_{b}))\). By Consistency we get the desired contradiction \(((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}_{k}),(h^{*},c''_{a}),(h^{*},c''_{b}))\) \(\mathbf{R }(e)((h^{*},\widehat{c}_{j}),(h^{*},\widehat{c}_{k}),(h^{*},c'''_{a}),(h^{*},c'''_{b}))\).
In the final part of this second step of the proof we show that for any pair of allocations \(z_{N},z'_{N}\in Z^{n}\) such that \(\min _{i\in N}\lambda _{i}(z_{N})>\min _{i\in N}\lambda _{i}(z'_{N})\), social preferences over these two allocations are characterised by \(z_{N}\mathbf{P }(e)z'_{N}\). Let us then assume \(z_{N},z'_{N}\in Z^{n}\) with \(\min _{i\in N}\lambda _{i}(z_{N})>\min _{i\in N}\lambda _{i}(z'_{N})\). Due to the properties of the ORPs it is possible to define two perfect health allocations \(x_{N},x'_{N}\in Z^{n}(h^{*})\) such that for all \(i\in N\) we have \(\lambda _{i}(z_{N})>\lambda _{i}(x_{N})\) and \(\lambda _{i}(x'_{N})>\lambda _{i}(z'_{N})\). Additionally, let \(i_{0}\in N\) be such that \(\lambda _{i_{0}}(z'_{N})=\min _{i\in N}\lambda _{i}(z'_{N})\), where
Let \(Q=N\setminus \{i_{0}\}\), and let us define a sequence of allocations \((x^{q}_{N})_{1\le q\le \mid Q\mid +1}\) such that for all \(i\ne i_{0}\)
and
This sequence implies that \(\lambda _{q}(x^{q}_{N})>\lambda _{q}(x^{q+1}_{N})>\lambda _{i_{0}}(x^{q+1}_{N})>\lambda _{i_{0}}(x^{q}_{N})\), with \(\lambda _{i}(x^{q}_{N})=\lambda _{i}(x^{q+1}_{N})\) for all \(i\ne q,i_{0}\). Consequently, and as we have previously proved, it must be the case that \(x^{q+1}_{N}\mathbf{P }(e)x^{q}_{N}\) for all \(q\in Q\). Moreover, by construction of x and \(x'_{N}\) we have both \(z_{N}\mathbf{P }(e)x^{\mid Q\mid +1}_{N}\) and \(x^{1}_{N}\mathbf{P }(e)z'_{N}\), and hence by Transitivity we finally get that \(z_{N}\mathbf{P }(e)z'_{N}\).
Step 3: Lexicographic order of\({\mathbf{R }}^{\lambda }_{\mathrm{lex}}\)We extend the previous result in order to meet the lexicographic criterion, that is, we show that whenever \((\lambda _{i}(z_{N}))_{i\in N}\ge _{\mathrm{lex}}(\lambda _{i}(z_{N}))_{i\in N}\), with at least one strict inequality, then \(z_{N}\mathbf{P }(e)z'_{N}\). Without loss of generality, let us assume that there exist \(j,k\in N\) such that \(\min _{i\in N}\lambda _{i}(z_{N})=\lambda _{j}(z_{N})=\lambda _{k}(z'_{N})=\min _{i\in N}\lambda _{i}(z'_{N})<1\). If the value of this minimum equivalent is different to the one proposed here, we can construct the allocations by means of Strong Pareto and Perfect Consumption Scale Independence. Additionally, let us assume that \(\min _{i\in N\setminus \{j\}}\lambda _{i}(z_{N})=\lambda _{k}(z_{N})>\lambda _{j}(z'_{N})=\min _{i\in N\setminus \{k\}}\lambda _{i}(z'_{N})\). The fact that these values are given by agents j and k can always be generated by Step 1 and Strong Pareto. To obtain the desired result we need to distinguish between four different cases.
Case 1: \(\lambda _{j}(z'_{N})<\lambda _{k}(z_{N})<1\). By Strong Pareto we have that \(z^{*}_{N}\mathbf{I }(e)z_{N}\), where \(z^{*}_{N}\in Z^{n}(h^{*})\) is the allocation in which for every individual i we have both \(h_{i}=h^{*}\) and \(z_{N}^{*}I_{i}z_{N}\). Likewise, we obtain \(z^{*'}_{N}\mathbf{I }(e)z'_{N}\). Let us now include one additional agent a who shares ORPs with individual j, that is \(R_{a}=R_{j}\in {\mathcal {R}}\), and who enjoys a health-consumption bundle \(z_{a}^{*}=(h^{*},c^{*}_{a})\in Z\) such that \(c^{*}_{a}>c^{*}_{e}(\widehat{R}_{j})\). According to Consistency and Well-being Bound Transfer we establish that \(({z}^{*'}_{N\setminus \{k\}},{z}^{*''}_{k},{z}^{*'}_{a})\mathbf{I }(e)({z}^{*'}_{N},{z}^{*}_{a})\), where \({z}^{*''}_{k},{z}^{*'}_{a}\in Z\) are the (perfect health) bundles that satisfy, respectively, \(c^{*''}_{k}/c^{*}_{e}(\widehat{R}_{k})=c^{*}_{a}/c^{*}_{e}(\widehat{R}_{j})>1\) and \(c^{*'}_{k}/c^{*}_{e}(\widehat{R}_{k})=c^{*'}_{a}/c^{*}_{e}(\widehat{R}_{j})<1\). By Priority Among Equals we get that \(({z}^{*'}_{N\setminus \{j,k\}},{z}^{*}_{j},{z}^{*''}_{k},{z}^{*''}_{a})\mathbf{I }(e)({z}^{*'}_{N\setminus \{k\}},{z}^{*''}_{k},{z}^{*'}_{a})\), where \({z}^{*''}_{a}={z}^{*'}_{j}\in Z\). If we apply Well-being Bound Transfer once again we have that \(({z}^{*'}_{N\setminus \{j,k\}},{z}^{*}_{j},{z}^{*'''}_{k},{z}^{*}_{a})\mathbf{I }(e)({z}^{*'}_{N\setminus \{j,k\}},{z}^{*}_{j},{z}^{*''}_{k},{z}^{*''}_{a})\), where \({z}^{*'''}_{k}\in Z\) is the bundle that satisfies \(c^{*'''}_{k}/c^{*}_{e}(\widehat{R}_{k})=c^{*''}_{a}/c^{*}_{e}(\widehat{R}_{j})<1\). According to the values of the \(\lambda \)-relative equivalents and Strong Pareto, we know from Step 2 that \({z}^{*}_{N\setminus \{j\}}\mathbf{P }(e)({z}^{*'}_{N\setminus \{j,k\}},{z}^{*'''}_{k})\). If we apply Consistency and Transitivity we get that \(({z}^{*}_{N},{z}^{*}_{a})\mathbf{P }(e)({z}^{*'}_{N\setminus \{j,k\}},{z}^{*}_{j},{z}^{*'''}_{k},{z}^{*}_{a})\mathbf{I }(e)({z}^{*'}_{N},{z}^{*}_{a})\). By means of Consistency and Transitivity we reach the desired result \(z_{N}\mathbf{P }(e)z'_{N}\).
Case 2: \(\lambda _{k}(z_{N})=1>\lambda _{j}(z'_{N})\) or \(\lambda _{k}(z_{N})>1>\lambda _{j}(z'_{N})\). The final result can be easily obtained by using the same line of reasoning that we have applied in the previous case.
Case 3: \(\lambda _{k}(z_{N})>\lambda _{j}(z'_{N})>1\). By Strong Pareto we have both \(z^{*}_{N}\mathbf{I }(e)z_{N}\) and \(z^{*'}_{N}\mathbf{I }(e)z'_{N}\), where \(z^{*}_{N}\) and \(z^{*'}_{N}\) are constructed exactly as before. According to the values of the \(\lambda \)-relative equivalents and Strong Pareto we have \({z}^{*}_{N\setminus \{j\}}\mathbf{P }(e)({z}^{*'}_{N\setminus \{j,k\}},{z}^{*'''}_{k})\), where \({z}^{*'''}_{k}\in Z\) is the bundle that satisfies \(c^{*'''}_{k}/c^{*}_{e}(\widehat{R}_{k})=c^{*'}_{j}/c^{*}_{e}(\widehat{R}_{j})>1\), and by Consistency we get that \({z}^{*}_{N}\mathbf{P }(e)({z}^{*'}_{N\setminus \{j,k\}},{z}^{*}_{j},{z}^{*'''}_{k})\). Given that \(\lambda _{j}(z^{*}_{N})=\lambda _{k}(z^{*'}_{N})<1\) and \(\lambda _{j}(z^{*'}_{N})=\lambda _{k}(z^{*'''}_{N})>1\), by Well-being Bound Transfer we obtain that \(({z}^{*'}_{N\setminus \{j,k\}},{z}^{*}_{j},{z}^{*'''}_{k})\mathbf{I }(e){z}^{*'}_{N}\). Again, by means of Strong Pareto and Transitivity we reach the desired result \(z_{N}\mathbf{P }(e)z'_{N}\).
Case 4: \(\lambda _{k}(z_{N})>\lambda _{j}(z'_{N})=1\). Once more, we construct \(z^{*}_{N},z^{*'}_{N}\in Z^{n}\). Next, let us assume alternative allocations \(z^{*''}_{N},z^{*'''}_{N}\in Z^{n}\) such that for all \(i\in N\) we have that \(h_{i}=h^{*}\), and moreover \(c^{*''}_{i}=\beta c^{*}_{i}\) and \(c^{*'''}_{i}=\beta c^{*'}_{i}\), with \(\beta \in (0,1)\). Because of continuity it is possible to find such allocations with \(\lambda _{k}(z^{*''}_{N})>1\) and \(\lambda _{j}(z^{*'''}_{N})<1\). From previous results we know that \(z^{*''}_{N}\mathbf{P }(e)z^{*'''}_{N}\). Using Perfect Consumption Scale Independence we get that \(z^{*}_{N}\mathbf{P }(e)z^{*'}_{N}\), and then by Strong Pareto and Transitivity we reach again the desired result \(z_{N}\mathbf{P }(e)z'_{N}\).
Step 4: Independence of the SO axioms To conclude the proof we additionally show that the five normative requirements are independent, and hence if one of them is dropped it is possible to find a SOF which does not satisfy Theorem 1.
-
(1)
Drop Strong Pareto Take \(\mathbf{R }\) defined as the application of the lexicographic minimax criterion over \((\lambda _{i}(z_{N}))_{i\in N}\). This rule establishes that a group of objects \(a_{N}\in {\mathbb {R}}^{n}\) dominates any other group \(b_{N}\in {\mathbb {R}}^{n}\) if the highest value in \(a_{N}\) is lower than the highest value in \(b_{N}\). If they are identical, then society eliminates these maximal elements and compares the highest values in the reduced allocations, and so on. The fact that \(\mathbf{R }\) satisfies Consistency and Perfect Consumption Scale Independence is straightforward. According to Well-being Bound Transfer, social welfare does not decrease when we move from allocation \(z'_{N}\) to \(z_{N}\) such that \(\lambda _{j}(z'_{N})>\lambda _{j}(z_{N})>1>\lambda _{k}(z_{N})>\lambda _{k}(z'_{N})\). Therefore, this axiom is also satisfied by \(\mathbf{R }\). The case of Priority Among Equals is shown in a similar way.
-
(2)
Drop Consistency Consider \({\mathbf{R }}^{\lambda ^{+}}_{\mathrm{lex}}\) defined exactly as \({\mathbf{R }}^{\lambda }_{\mathrm{lex}}\) but assuming, for all \(i\in N\), that \(c^{*}_{e}(\widehat{R}_{i})\) is constructed using \(m^{+}\) instead of \(m^{-}\). Let \(\mathbf{R }\) now coincide with \({\mathbf{R }}^{\lambda ^{+}}_{\mathrm{lex}}\) if there exists \(i\in N\) such that \(m_{i}=m^{+}\), and with \({\mathbf{R }}^{\lambda }_{\mathrm{lex}}\) otherwise. With the exception of Consistency, all axioms are satisfied by \(\mathbf{R }\) since it is constructed exactly as \({\mathbf{R }}^{\lambda }_{\mathrm{lex}}\).
-
(3)
Drop Perfect Consumption Scale Independence Take \(\mathbf{R }\) defined as the application of the lexicographic minimax criterion over \((\rho _{i}(z_{N}))_{i\in N}\), where \(\rho _{i}(z_{N})=c^{*}_{e}(\widehat{R}_{i})(1-\lambda _{i}(z_{N}))\), for all \(i\in N\). The fact that \(\mathbf{R }\) satisfies Strong Pareto and Consistency is straightforward. According to Well-being Bound Transfer, social welfare does not decrease when we move from allocation \(z'_{N}\) to \(z_{N}\) such that \(c^{*}_{e}(\widehat{R}_{j})(1-\lambda _{j}(z'_{N}))>c^{*}_{e}(\widehat{R}_{j})(1-\lambda _{j}(z_{N}))>0>c^{*}_{e}(\widehat{R}_{k})(1-\lambda _{k}(z_{N}))>c^{*}_{e}(\widehat{R}_{k})(1-\lambda _{k}(z'_{N}))\). Therefore, this axiom is also satisfied by \(\mathbf{R }\). The case of Priority Among Equals is shown in a similar way.
-
(4)
Drop Priority Among Equals Let \(\mathbf{R }\) be defined such that for all \(e\in {\mathcal {E}}\) and \(z_{N},z'_{N}\in Z^{n}\), \(z_{N}\mathbf{R }(e)z'_{N}\) if \(\sum _{i\in N}\mu _{i}(z_{N})\ge \sum _{i\in N}\mu _{i}(z'_{N})\), where \(\mu _{i}(z_{N})=\lambda _{i}(z_{N})c^{*}_{e}(\widehat{R}_{i})\). The fact that \(\mathbf{R }\) satisfies Strong Pareto, Consistency and Perfect Consumption Scale Independence is straightforward. Note that \(\mu _{i}(z_{N})\) is the individual i’s level of consumption when she has perfect health. Therefore, since Well-being Bound Transfer is defined by assuming balanced transfers this axiom is also satisfied by \(\mathbf{R }\). In other words, no transfer reverses the social preferences.
-
(5)
Drop Well-being Bound Transfer Take \(\mathbf{R }\) defined such that for all \(e\in {\mathcal {E}}\) and \(z_{N},z'_{N}\in Z^{n}\), \(z_{N}\mathbf{R }(e)z'_{N}\) if \((\mu _{i}(z_{N}))_{i\in N}\ge _{\mathrm{lex}}(\mu _{i}(z'_{N}))_{i\in N}\), where \(\mu _{i}(z_{N})\) is defined as in the previous case. The fact that \(\mathbf{R }\) satisfies all the four remaining axioms is straightforward. Note that Perfect Consumption Scale Independence changes \(\mu _{i}(z_{N})\), that is, the individual i’s level of consumption when she has perfect health, in the same proportion for all individuals, and hence the lexicographic ranking does not change.
Consequently, any SOF that satisfies Strong Pareto, Consistency, Perfect Consumption Scale Independence, Priority Among Equals and Well-being Bound Transfer is grounded on the application of the leximin criterion over the \(\lambda \)-relative equivalents. Other social rankings may also satisfy all these requirements, although the combination of the five axioms single out \({\mathbf{R }}^{\lambda }_{\mathrm{lex}}\).
Rights and permissions
About this article
Cite this article
Calo-Blanco, A. Health and fairness with other-regarding preferences. Rev Econ Design 24, 123–141 (2020). https://doi.org/10.1007/s10058-020-00235-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10058-020-00235-2