A granular thermometer

Abstract

The behaviour of granular materials is known to be strongly affected by the granular temperature, which is a measure of the intensity of particle vibration. However, no experimental technique exists to measure the granular temperature and its variation inside arbitrary media during deformation. Here, we present a new experimental technique for measurement of this granular temperature field by tracking tracer particles over time, using X-ray radiography with two simultaneous orthogonal source/detector pairs. We show that errors in particle tracking lead to systematic measurement biases. The main sources of these biases are identified and methods for their quantification are developed so that unbiased results can be calculated. The new granular thermometry technique is validated against discrete element simulations. Finally, an experimental example is shown for the case of a vibro-fluidised system, where we find that the granular temperature is highest at the free surface.

Graphical Abstract

1 Introduction

Flowing granular materials are poorly understood despite their ubiquity in nature and industrial processes. There is growing evidence that we may need an additional state variable that would assist in describing the rich phenomena observed in granular flows, such as segregation [1, 2], non-locality [3,4,5], phase transitions [6], and instabilities [7]. This aforementioned state variable is typically described as being dependent on the velocity fluctuations of the grains and has been variously identified as the granular temperature [6], fluidity [3], kinetic pressure [2], or granular diffusivity [4]. The concept of velocity fluctuation is well known in the fields of colloid rheology [8], metallurgy [9], soft matter chemistry [10], and turbulent fluid dynamics [11].

Experimental measurements of granular materials are often coarse and only provide global properties of the whole sample. Local measurements can also be made, but due to the opaque nature of granular materials, are usually limited to quasi-two-dimensional systems or to the boundaries of three-dimensional systems. Internal behaviour is typically inferred via numerical simulations (e.g. using discrete element method simulations), although advances in experimental techniques now allow the evolving internal structure to be probed.

A variety of technologies exist to obtain information about the internal kinematics of a granular medium, such as X-ray or neutron tomography [12, 13], Positron Emission Particle Tracking (PEPT) [14], Refractive Index Matched Scanning (RIMS) [15], Magnetic Resonance Imaging (MRI) [16], Magnetic Particle Tracking (MPT) [17], Three Dimensional Particle Tracking Velocimetry (3D PTV) [18], and X-ray rheography [19], as well as combinations of these techniques [20]. Several of these techniques require motion to be suspended during imaging (e.g. tomography), whilst others require specialised materials (MRI, RIMS). Two promising technologies, PEPT and radiography, overcome these limitations and can be used to calculate the granular temperature in arbitrary media. Here, we use X-ray radiography as our measurement technique, due to its ease of use, well defined measurement errors, and availability.

Dynamic X-ray radiography is an unobtrusive method that can be used to reliably describe the internal kinematics of granular flows over a wide range of temporal and spatial scales. Recently, correlation-based methods have been employed with dynamic X-ray radiography to successfully measure macroscopic velocity fields in three-dimensional systems, both in a 2D beam-averaged sense [21, 22] and fully 3D measurements [19].

Building on these advances in dynamic X-ray technology, this paper introduces and verifies a measurement technique for characterising velocity fluctuations in granular media. The technique relies on locating tracer particles in a series of paired X-ray radiographs, and triangulating the tracer’s three-dimensional location, and consequently velocity. We verify the technique by applying it to sets of artificial radiographs produced by discrete element simulations. Additionally, we present a careful error analysis of the technique, which shows how to quantify and correct for systematic biases in the resulting granular temperature measurements. Finally, we conclude with experimental measurements of the granular temperature in a vibro-fluidised convective granular system.

2 Granular thermometry

The canonical definition of granular temperature, in direct analogy with conventional temperature, is the expected value of the square of the fluctuating instantaneous particle velocities [23, 24]. When defined in this way the granular temperature is a purely kinematic variable that describes the fluctuations of translational kinetic energy only when local and particle densities are homogeneous across the domain, ignoring kinetic energy of other degrees of freedom such as rotational ones. The analogy with conventional temperature holds when grains are of similar size, made of the same material, and when local density gradients are small or non existent. In addition, this definition ignores any energy fluctuation in the grains themselves, which could arise from elastic potential change or heat transfer for example.

There is as yet no universally accepted approach to take into account the contribution of the density to the fluctuating kinetic energy, although several models exist, e.g. [6, 25, 26].

In general, these definitions depend on functions of the range of local density measurements of the bulk particles. While it may be possible to measure the coarse grained local density, this measurement introduces additional uncertainty into the result. For flowing near-spherical glass beads, the range of densities is quite narrow, and the experimental uncertainty on the density would dominate any measurement of the temperature.

To avoid confusion, and for the sake of consistency, we therefore adopt the following definition of $T_{g}$ [23, 24] that is based solely on particle velocity measurements. Assuming the instantaneous velocity of a given grain is denoted $\varvec{v}$, we can define the fluctuating component $\varvec{v}'$ as

$$\begin{aligned} \varvec{v}'&= \varvec{v} - {\mathbb {E}}[\varvec{v}], \end{aligned}$$

(1)

where ${\mathbb {E}}$ denotes the expected value, representing an ensemble average at the current location of the grain in space and time. For steady-state systems, or systems that evolve slowly compared to the measurement duration, this ensemble average can be replaced by temporal averaging over a time window. Similarly, ensemble averaging in spatially homogeneous systems, or with weak spatial gradients, can be approximated by averaging observations at different spatial positions.

Assuming a well-defined averaging window exists, and following [27], we can then define the true granular temperature $T_{g}$ as

$$\begin{aligned} T_{g}&= \tfrac{1}{D}{\mathbb {E}}\left[ ||\varvec{v}'||^2\right] , \end{aligned}$$

(2)

where $D=3$ is the dimensionality of the system and $||\varvec{v}'||$ represents the standard Euclidean norm. In contrast to the conventional microscopic definition of temperature, granular systems cannot be maintained at a non-zero granular temperature, $T_{g}$, whilst also being in equilibrium, as without external excitation the granular temperature always decays to zero [6, 24]. This means that a priori we cannot build a granular thermometer which can measure the granular temperature at equilibrium. One way of overcoming this limitation is to directly measure the instantaneous fluctuation velocities of individual particles from (1), and to calculate $T_{g}$ from these measurements using (2) for steady-state systems (which is the focus of this paper).

Previous measurements of the granular temperature have been performed using a variety of experimental methods. Direct measurement of particle locations over time have been performed optically (e.g. Particle Image Velocimetry, both in 2D [28,29,30,31,32] and in 3D [33, 34], or via PEPT [35,36,37]). The granular temperature has also been indirectly measured via MRI [38], acoustic shot measurement [39], diffusing wave spectroscopy [40], laser Doppler velocimetry [41], speckle visibility spectroscopy [42], or acoustic energy measurement [43]. Most of these techniques measure a single bulk temperature value for all of the particles, or are limited to two-dimensional systems or the boundaries of three dimensional systems. PEPT and X-ray radiography, however, are two of the most promising methods for making full three-dimensional measurements.

Here, the proposed granular thermometer tracks the three-dimensional locations of one or more individual particles from a series of radiographs. From these reconstructed trajectories, it is then possible to calculate the velocities of the particles between frames and consequently the velocity fluctuations of tracked particles in steady-state systems. Finally, the variance of all of the velocity fluctuations measured in the trajectories crossing a given region of space is computed, leading to the first three-dimensional experimental measurement of the field of granular temperature $T_{g}$ in dense granular flows.

This method bears similarities with a traditional thermometer. To measure the temperature of a gas or liquid, we typically immerse our thermometer in that medium, let it reach equilibrium, and then with knowledge of the calibration of our thermometer, one can infer the temperature of the medium of interest. In this case, we shall measure the temperature of tracer particles, which will need to be carefully calibrated to infer the temperature of the bulk particles.

3 Methodology

Fig. 1

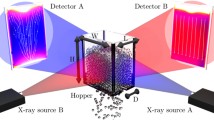
Schematic representation of the experimental setup. Two orthogonal X-ray tube/detector pairs produce orthogonal radiographs of the granular medium. The granular medium (shown in blue) is being vibrated from below by a vibration stage attached to a cylindrical piston. A hollow cylindrical, fixed (non-vibrating) wall surrounds the grains, separated from the piston by a $\sim \,0.5\,\hbox {mm}$ gap and one tracer particle of higher attenuation is shown in black. Stream lines of the flowing material are shown in yellow. Note that dimensions are not to scale. The aluminium frame that holds the cylinder is omitted from the sketch for clarity. Inset: Schematic cross section of the cylindrical container with glass beads (blue), tracer particle (black) and stream lines (red) depicted (color figure online)

3.1 Radiograph acquisition

The X-ray data acquisition apparatus is shown in Fig. 1. It consists of two X-ray sources and two Varex Imaging PaxScan 2520DX detectors. The sources generate polychromatic X-rays with voltage of 130 kVp and current of 3.6 mA in the shorter direction, and 7.4 mA in the longer direction. The detector panels can record at up to 30 Hz at a spatial resolution of $968\times 760$ pixels. The depicted layout allows for simultaneous recording of the experiment from two orthogonal directions. Each direction is used to deduce the two in-plane positions of the tracer particles, and combining them makes it possible to reconstruct three-dimensional trajectories, and consequently granular temperature fields.

The procedure for tracking tracer particles is shown in Fig. 2. This process relies on finding particles that are systematically distinguishable from the other particles, and so in this work we use glass beads as the bulk particles, and steel particles as the tracer particles we aim to track. Because of the higher X-ray attenuation coefficient of steel relative to glass, it is possible to identify steel particles systematically, showing up as lower intensity, or darker, regions of the X-ray radiograph. A visual summary of this methodology is also provided in SI Video 1. We expect the steel tracers to have different velocities and $T_{g}$ fields to the bulk particles [1, 44] caused by significant difference in density from the bulk particles. We will present in “Appendix 1” a method for making the connection between the bulk and tracers granular temperatures.

As shown in Fig. 2a–c, we normalize the raw radiographs by dividing them by the time average of each pixel across the whole experiment. In this way, the value at each pixel represents whether the current location has a higher or lower attenuation than average. This removes intensity gradients across the width of radiographs, mostly visible at its vertical edges, that are caused by the differing X-ray path length through the medium, and from X-ray scattering.

3.2 Tracer tracking algorithm

In each normalized radiograph we search for any tracer particles based on their higher X-ray absorption. We define the tracer’s position as its centroid, since the tracer is a sphere, and attempt to find the location of this centroid in each radiograph. As the tracer particle is projected onto the radiograph by a conical X-ray beam, the projection is in general an ellipse. However, given our geometry (Fig. 1), the projection can be closely approximated by a circle. We therefore define the tracer as a circular disk whose intensity is the lowest of all possible circular disks in the radiograph.

Fig. 2

Tracer tracking procedure. a Time averaged radiograph, b radiograph of experiment with four tracer particles, and c normalised radiograph. The brightness and contrast have been adjusted for clarity. Normalisation enhances the contrast between the tracers and bulk, reduces intensity gradients across the width and eliminates the background. d Patch with visible tracer. A convolution kernel is applied across the whole patch and the e convolution map is populated. The minimum in the convolution map is defined as the center of the tracer particle

To achieve sub-pixel accuracy of measurements, the normalized image is bilinearly interpolated onto a grid 10 times finer, so that the positions are measured to 0.1 pixel precision. To find the darkest circular disk we sum the values of the normalized pixel intensities within a circular patch of known diameter $d_{int}$. The value of $d_{int}$ is calculated from the geometry of the experiment, since the sizes of the tracer and detector are known. We repeat this process for all possible locations of the circular patch within the image. The location where the sum of all pixels is the lowest is the darkest disk in the radiograph and therefore represents our tracer location (Fig. 2e).

3.3 Reconstruction of trajectories

At each recording time t, two radiographs are produced, one from each source/detector pair. By applying the algorithm developed above, we can measure the particle’s in-plane location in each of these two radiographs. In general, the three-dimensional particle location in the laboratory reference frame is the intersection of the two lines which pass between the sources and the particle locations on the corresponding detector panels.

Note that due to the orthogonality of the source/detector pairs in this system, we have two measures of the particle height (the z direction, as shown in Fig. 7), which is useful for a consistency check and calibration purposes. After triangulation, we can recover the measured coordinates of the tracer in the laboratory frame of reference, denoted as $\widetilde{\varvec{x}}(t)=(\widetilde{x}(t), \widetilde{y}(t), \widetilde{z}(t))$.

3.4 Particle velocities

Using these measured trajectories, we can apply a forward difference scheme to approximate a particle’s velocity along this trajectory as

$$\begin{aligned} \widetilde{\varvec{v}}\left( \widetilde{\varvec{x}}\left( t_k\right) ,t_{k}\right) = \frac{\Delta \widetilde{\varvec{x}}}{\Delta { t}} = \frac{\widetilde{\varvec{x}} \left( t_{k+1}\right) -\widetilde{\varvec{x}} \left( t_{k}\right) }{t_{k+1} - t_k}, \end{aligned}$$

(3)

where $\Delta \widetilde{\varvec{x}}$ is the measured movement of the grain between recorded locations, $\Delta { t}$ is the time step and $\widetilde{\varvec{x}}(t_k)$ is the measured position of the particle at time $t_k$ (the time of the $k^{\mathrm {th}}$ recorded frame , where k is an ordinal number representing the order of the recorded radiographs). A central difference or other finite difference scheme could also be used for this calculation, but similar results are obtained..

We refer to the velocity calculated in this way (denoted $\widetilde{\varvec{v}}$) as the ‘measured velocity’ to distinguish it from the true instantaneous velocity $\varvec{v}$. The accuracy of $\widetilde{\varvec{v}}$ as an approximation to $\varvec{v}$ depends on the accuracy of the finite difference approximation (a function of the finite $\Delta { t}$) as well as the accuracy of the measured positions $\widetilde{\varvec{x}}(t_k)$ compared to the true particle positions $\varvec{x}(t_k)$.

3.5 Measuring granular temperature

The discrete set of measured particle velocities, say $\widetilde{\varvec{v}}_k$, is used to estimate the granular temperature of the system, which requires approximations of both the mean and instantaneous velocity fields of the bulk. For spatially homogeneous systems at steady-state, the most straightforward way to achieve this is to approximate the mean by the average of N particle velocity measurements. This can be written ${\mathbb {E}}[\varvec{v}] \approx \widetilde{\varvec{\mu }}$, where

$$\begin{aligned} \widetilde{\varvec{\mu }} = \frac{1}{N}\sum _{k=1}^N \widetilde{\varvec{v}}_k. \end{aligned}$$

(4)

The granular temperature can then be approximated by $T_{g} \approx \widetilde{T}_{g}$, where

$$\begin{aligned} \widetilde{T}_{g} = \frac{1}{3N}\sum _{k=1}^N ||\widetilde{\varvec{v}}_k-\widetilde{\varvec{\mu }}||^2. \end{aligned}$$

(5)

However, in most situations we anticipate that the mean velocity, as well as the granular temperature field itself, will depend on spatial position. To produce fields which are compatible with the equations of continuum mechanics, we therefore coarse-grain (e.g. [27, 45]) our particle measurements to produce approximations to the mean velocity field, $\widetilde{\varvec{\mu }}\approx {\mathbb {E}}[\varvec{v}]$, as well as $\widetilde{\varvec{\mu }^2}\approx {\mathbb {E}}[\varvec{v}^2]$. Using the equivalent definition of variance, the granular temperature approximation is then given by

$$\begin{aligned} \widetilde{T}_{g} = \frac{1}{3}||\widetilde{\varvec{\mu }^2} - (\widetilde{\varvec{\mu }})^2||. \end{aligned}$$

(6)

Further details of the coarse-graining procedure are given in “Appendix 1”.

Both ensemble averaging and coarse-graining produce granular temperature measurements that are an approximation to the true underlying value. Furthermore, because they use particle velocities measured over finite sampling windows, $\widetilde{\varvec{v}}$, rather than instantaneous velocities $\varvec{v}$, we expect the measured temperature $\widetilde{T}_{g}$ to differ from the true $T_{g}$. Nevertheless, it is anticipated that $\widetilde{T}_{g}\rightarrow {T_{g}}$ as $\Delta { t} \rightarrow {0}$, and this is investigated more closely in subsequent Sections.

4 Measurement verification

4.1 DEM simulations

To verify and validate the procedure described above, and the subsequent error analysis detailed in Sect. 5, we perform discrete element method (DEM) simulations (see Fig. 3) using MercuryDPM [46]. These simulations give us access to a large volume of data, including in particular, the instantaneous position and velocity of each particle at arbitrarily small time increments. We can use this information to make artificial radiographs and apply our tracking algorithm to these images, allowing systematic exploration of the accuracy of the method by comparing the obtained measurements with the true values from DEM simulations.

Simple shear simulations were performed with Lees-Edwards boundary conditions on boundaries with normals in the x and y directions, and periodic boundaries in the z direction. The length and height of the simulations (in the x and y directions) were set to 2 cm and the depth (in the z direction) to 10 cm. Particles were sheared in the x direction with a shear rate $|\dot{\gamma }|$ of ${0.5}{1/\hbox {s}}$. The packing density was set to 0.6, which yields 1690 particles, and the particle density taken to be 2478 kg/m$^{3}$, representative of glass. The particle diameter was set to ${3}\,\hbox {mm}$ ± ${20}{\%}$ to prevent crystallization. Collisions were modelled by a linear spring and viscous damper both in the normal and tangential direction, with a collision time of $t_{c}={10^{-3}}{\hbox {s}}$ and restitution coefficient of 0.95 calculated for typical collision velocities. The sliding friction coefficient was set to 0.5, and simulation time step to $t_d=t_c/10$. The total duration of the simulation is 15 s starting from the point of steady-state conditions (where the pressure and kinetic energy were relatively constant over time) and to ensure saturation of the granular temperature value.

Fig. 3

Sketch of 3D DEM simple shear setup with boundary conditions and parameters used in the simulation. The system is sheared in the x direction and is periodic in all directions. The length of the system into the page (the z direction) is 10 cm

4.2 Artificial radiographs

We generate artificial radiographs from this DEM data using the Beer-Lambert law as described in the Supplementary Material of [19]. The algorithm does not take into account the random noise of the X-ray beams, their polychromaticity, nor their scattering. Additionally, a parallel X-ray beam is modelled. We reconstruct artificial radiographs with the following resolutions: 333.5, 266.5, 200, 133.5, 66.5 and 33.5 px/cm. In these radiographs, the intensity of the incident beam is normalised to 1.0 and the ratio of the mass attenuation coefficients of steel and glass is taken to be 7.0 [47].

4.3 Verification of tracking algorithm

To ensure that the tracking algorithm successfully finds tracer particles, we compare their true in-plane locations obtained from DEM simulation with their measured positions from applying our tracking algorithm to the artificial radiographs (Fig. 4). These artificial radiographs are produced with a fictional parallel beam that points along the z axis. The measured particle positions give the x and y coordinates of the tracers, and we choose here to restrict our verification to the x direction.

Fig. 4

Comparison between tracer particle locations from exact DEM data (red) and radiograph tracking (black), at different spatial resolutions a 333.5 px/cm, b 266.5 px/cm, c 200 px/cm, d 133.5 px/cm, e 66.5 px/cm, and f 33.5 px/cm. $x^{sim}$ denotes the intruder x coordinate in meters, whereas $x^\text {rad}=x^\text {sim}/p$ is the equivalent value in pixels, with p the pixel size in meters. In all cases the radiograph tracking method accurately predicts the true position to within 0.1 pixels. The sampling rate is 0.001 s (color figure online)

When comparing the measured x coordinate of the tracer particle from the tracking algorithm with the true value from DEM data, we find the root mean square error between the true and measured coordinates to be less than 0.5 pixels, and also less than $1\%$ of a particle diameter.

4.4 Granular temperature measurements

To verify the final step of the granular thermometry procedure we use the particle-level information to calculate the granular temperature of the system, both from DEM instantaneous velocity data directly and from the reconstructed particle trajectories. For the subsequent calculations it is assumed that the granular temperature is homogeneous across the whole domain. The steady-state velocity field is spatially dependent and given by a simple linear profile controlled by the shear rate. The granular temperature is therefore calculated by using this linear profile in the ensemble average (5).

Despite the ability of our method to accurately measure the position of tracer particles over time, additional errors are introduced when using the position measurements to calculate the granular temperature of flowing granular material. These typical errors, and the associated bias on the resulting temperature measurements, are discussed in more detail in Sect. 5 below.

5 Measurement uncertainty and bias

We have identified six sources of error that potentially affect the granular temperature measurement. All of these are either minimised or explicitly quantified and corrected for. The sources of error are:

• 1. Missed collisions caused by the finite sampling rate of the detectors, which limits the temporal resolution of measurements, measuring a lower $T_{g}$ than the true value (by effectively assuming a constant velocity between successive frames), see Sects. 5.1 and “Appendix1”.

• 2. The finite pixel size on the detector panels, which limits the spatial resolution of the position measurements, artificially increasing the measured temperature, see Sects. 5.2 and “Appendix 1”.

• 3. Particle tracking errors due to the heterogeneity of granular materials. These errors are significant when the granular medium is deformed significantly between measurements, and this effect is quantified in detail in “Appendix 1”.

• 4. Sampling error due to the finite number of samples used to calculate the granular temperature. This can be neglected when using a sufficiently large number of samples, as outlined in “Appendix 1”.

• 5. Noise in the radiographs caused by source and detector imperfections and X-ray scattering. Calibration experiments have shown that the tracking algorithm is not measurably affected by this noise, and therefore this error can be neglected.

• 6. Misalignment of the experimental equipment can introduce a systematic bias in our position measurements. In the geometry proposed in Fig. 1, these effects are minimised by precise measurement and the relatively long distances between sources and detectors, as well as ensuring orthogonal X-ray paths.

In the configuration described in Sect. 6.1, the first two sources of experimental error are dominant, and we account for them explicitly in the results produced below. The other four sources of error have been quantified where possible, and we show here and in the Supporting Information how such quantification can be done and under which circumstances they could be significant.

5.1 Missed collisions

By only sampling tracer locations at finite time intervals, we inevitably miss collisions between particles. Since each of these missed collisions involves a change of direction, the net result is a reduction in the measured $\widetilde{T}_{g}$ compared to the true $T_{g}$. This should be accounted for when sampling times are slow relative to the collision time, which is extremely common in X-ray radiography and optical imaging. The reduction in temperature is modelled by assuming

$$\begin{aligned} \widetilde{T}_{g} = \frac{1}{\alpha }T_{g}, \end{aligned}$$

(7)

where the non-dimensional factor $\alpha >1$ is given by

$$\begin{aligned} \alpha&= \sqrt{\frac{9a_{1}}{4}\frac{\Delta { t}}{t_{i}} + 1}, \end{aligned}$$

(8)

where $t_{i}=d\sqrt{\rho /P}$ is the inertial time, d the grain size, $\rho$ the particle density, P the typical pressure and $a_{1}$ is a non-dimensional fitting parameter. See “Appendix 1” for the full derivation. To validate this model, we fit (8) to the measurements of granular temperature from the DEM simulations, where each measurement of $\widetilde{T}_{g}$ is calculated from the exact particle positions and finite difference velocity approximations at different $\Delta { t}$, and the exact $T_{g}$ uses instantaneous particle velocities. Figure 5 shows the model fit to different measurements of $\widetilde{T}_{g}$ where the best fit of the constant $a_{1}$ is found to be 0.31.

Fig. 5

Missed collisions model (8) fit to DEM data as a function of non-dimensional time step. Inertial number $I=$ ${1.3\times {10^{-3}}}$, shear rate $|\dot{\gamma }|=$ ${0.5}{1/\hbox {s}}$, and inertial time $t_{i}=$ ${2.6\times {10^{-3}}\hbox {s}}$. a Main figure on log-log scale, b $\alpha ^2-1$ against non-dimensional time

As can be seen in Fig. 5, when the frame rate $\Delta { t}<0.1t_{i}$, the measured value is approximately equal to the true value ($\alpha =1$). This range of sampling times is referred to as the ballistic regime [4]. If particles are sampled fast enough to be in this regime, as in [35], this source of uncertainty can be neglected. At slower frame rates, higher velocities are less likely to be captured, thus the measured values of granular temperature become smaller and the value of $\alpha$ increases.

5.2 Finite pixel size

The finite pixel size of the detectors introduces an uncertainty in the measurement of the particle positions. It has been shown previously [48] how this uncertainty propagates to become a systematic bias in the measured granular temperature. From this effect, the measured $\widetilde{T}_{g}$ is actually larger than the the true value $T_{g}$, specifically

$$\begin{aligned} \widetilde{T}_{g}&= T_{g} + \Delta { T}_{g}^{\mathrm {res}}, \quad {\mathrm {where}} \quad \Delta T_{g}^{\mathrm {res}} = \frac{1}{6}\left( \frac{p}{\Delta { t}} \right) ^{2}, \end{aligned}$$

(9)

where p is the length in meters of the pixels and $1/\Delta { t}$ is the frame rate. In the experiments reported here, $p={1.1\times {10^{-2}}\,{\hbox {mm}/\hbox {px}}}$. A full derivation is shown in “Appendix 1”.

Fig. 6

Histograms of measured granular temperatures before (blue) and after (orange) corrections in accordance with (10). Each measured $\widetilde{T}_{g}$ is calculated for different resolution (p)/time step ($\Delta { t}$) pairs. True value of granular temperature calculated from instantaneous velocities is in green. Corrections are made for missed collisions and finite pixel size, omitting the negligible errors from other sources

5.3 Error correction

Having modelled the effect of finite pixel size and missed collisions on the granular temperature measurements, we can combine Eqs. (7) and (9), and potentially any additive bias $\Delta { T}^\mathrm {i}_{g}$, to express the corrected granular temperature, $T_{g}^\mathrm {cor}$, as

$$\begin{aligned} T_{g}^{\mathrm {cor}}&= \alpha \left( \widetilde{T}_{g} - \sum \Delta T^{\mathrm {i}}_{g}\right) = \alpha \left( \widetilde{T}_{g} - \Delta { T}_{g}^{\mathrm {res}}\right)\nonumber \\&= \sqrt{\frac{9a_{1}}{4}\frac{\Delta { t}}{t_{i}} + 1}\left( \widetilde{T}_{g} - \frac{1}{6}\left( \frac{p}{\Delta { t}}\right) ^{2}\right) . \end{aligned}$$

(10)

Figure 6 shows a histogram of these corrected measurements (in orange) at different time steps and resolutions, as well as the raw uncorrected measurements (blue) and the true granular temperature (green). We see that the corrected values represent a good approximation to the true temperature, and a major improvement on the uncorrected values. In particular, the mean of the corrected values is ${7.93\times 10^{-6}}$ ${\hbox {m}^{2}/\hbox {s}^{2}}$, compared to the true value of ${8.29\times 10^{-6}}$ ${\hbox {m}^{2}/\hbox {s}^{2}}$. The standard deviation of the corrected values around the true temperature is ${1.39\times 10^{-6}}$ ${\hbox {m}^{2}/\hbox {s}^{2}}$, or approximately 17% of the true temperature. The residual errors after error correction are therefore minimal.

Inspecting the results more closely, we find that the temperature correction (10) works well for values of $\tfrac{p}{\Delta { t}}=0.006$ m/s and smaller, but underestimates $T_{g}$ at larger values. This drop is caused by high values of $\Delta T_{g}^{\mathrm {res}}$, suggesting that the model for errors caused by finite resolution overestimates the bias for extremely high frame rates and extremely low resolutions. In the case of our experimental apparatus, given we have sub-pixel resolution to the level of 1/10th of an original pixel, the approximate value of $\tfrac{p}{\Delta { t}}$ is ${7.62\times 10^{-4}}$ m/s and hence the correction should work well.

Finally, note that our granular thermometry procedure, and subsequent error corrections, give the granular temperature of the intruder particle. This may not, in general, be the same as the temperature of the bulk particles, due to differences in at least size, shape, stiffness and density. If desired, an additional correction factor can be applied to infer the granular temperature of the bulk particles from the corrected measurement of the tracer particles. This is detailed in “Appendix 1”, where we use DEM simulation to determine that the corrected values should be scaled down by an additional factor of 1.5 for our particular system.

6 Vibro-fluidised bed

6.1 Experimental setup

Here we show the application of the granular thermometer to a vibro-fluidised granular bed experiment, which is shown schematically in Fig. 1. The experiment consists of a base piston attached to a vibrating stage, with an immobile hollow cylinder mounted on a static frame. The hollow cylinder has an internal diameter of 100 mm and is filled with 710 g of ${3}\,\hbox {mm}\pm {10}{\%}$ silicate glass beads to a height of approximately 60 mm and four steel tracer beads of the same size. In this experimental geometry, and with the dimensions indicated in Fig. 1, the artificially enhanced spatial resolution is approximately ${1.1\times {10^{-2}}{\hbox {mm}/\hbox {px}}}$ which is 273 pixels per intruder’s diameter. The vibrating stage is driven by a Syntron V-50 electromagnetic vibrator at the bottom of the top plate. The vibrator is an impact vibrator with a 50 Hz stroke frequency and power usage up to 530 W, which is large enough that the vibrating stage is not measurably affected by the weight of grains sitting on top of it. The vibrating stage piston is in direct contact with the grains, but not in contact with the hollow cylinder, so that vibrations of the walls are minimised.

6.2 Results

Fig. 7

Trajectory reconstruction for experimental data over 167 s. a Trajectory of intruder particle in 3D with orientation of Cartesian and cylindrical axes. b Representation of intruder’s trajectory in the rz half-plane with coarse-graining grid. Domain of the experiment is depicted in blue

The observed trajectory for a single tracer particle over 167 seconds is shown in Fig. 7. In total, four tracers are tracked for a cumulative 11,163 seconds. This 3D location information is then coarse-grained [45, 49] onto the 2D rz half-plane, as the system is axially symmetric, as seen in Fig. 7b. Details of this transformation and the related coarse-graining functions are shown in “Appendix 1”. This allows extraction of the temperature $\widetilde{T}_{g}$ as outlined in Sect. 3, which is then corrected following (10) using the values in Table  1. In Fig. 8 we show the occupancy (the probability of finding the intruder at a given location), steady-state velocity, shear rate, and predicted true granular temperature fields.

Table 1 Experimental values used for error correction

The system is excited only at the base, yet the $T_{g}$ field is not largest at this location. In fact the granular temperature starts high at the bottom, lowers in the middle and then rises to its maximum value at the free surface. Similar results were reported for vibrated granular gases by [36]. In the radial direction, the granular temperature is low at the central axis and grows until it reaches its maximum at the vertical boundaries. This trend bears similarity with the shear rate, which is also maximal at the vertical boundaries and free surface.

Fig. 8

Coarse-grained fields in the rz half plane, obtained from experimental measurement of intruder positions. a Occupancy profile, b steady-state velocity, c shear rate and d corrected granular temperature

7 Conclusion

Here we have presented a technique for the reconstruction of tracer trajectories in dense granular flows. The technique relies on dynamic X-ray radiography, which is able to penetrate beyond the boundaries of the material and can be used to observe the behaviour of the interior. Trajectories obtained in this way were used to calculate steady-state kinematic properties of the flow—steady-state velocity fields, their fluctuations and the granular temperature field.

We have presented a rigorous assessment of the effects of tracking errors on the measurement of the granular temperature field, and have quantified the systematic biases that affect this measurement. Additionally, using DEM simulations, we have proposed a method to identify and correct for these biases. After error correction, the residual errors were typically small in magnitude compared to the magnitude of the true temperature, especially at the timescales and resolutions of radiographic acquisition equipment. This substantiates the new technique as being suitable for observing and quantifying flow kinematics in laboratory experiments. Finally, we demonstrate this tracking algorithm and bias correction on a vibro-fluidised bed experiment.

Yet, there are questions remaining to be answered. First, from the experimental point of view, is whether we can reliably use this thermometer to infer the temperature of bulk particles from the temperature of denser tracer. Starting point would be development of novel segregation models that can be calibrated using combination of our experimental technique and DEM simulations, accompanied with cross calibration of our method with experimental methods that can measure kinematics of tracers with the same properties as the bulk, such as PEPT. Another approach would be to limit the calibration to two dimensional systems for which high speed cameras can be effectively used. Second question is related to the nature and definition of granular temperature and significance of velocity fluctuations and other fluctuations in dense granular flows. Granular temperature, as a measure of the energy at the granular scale, includes the contribution from fluctuations from both the kinetic energy and elastic potential. In dense flow regime, those two contributions are presumably of the same order of magnitude, and such system exhibits two modes of velocity fluctuations—one where particles are in free flight mode and velocity fluctuations are quadratic, and the second one where particles resemble network of harmonic oscillators caused by enduring contacts between themselves where the quadratic dependence on the velocity fluctuations will turn into a linear one. Thus, further research is needed in direction of defining the concept of granular temperature in sense of physically measurable quantities alongside with classification and measurements of fluctuation contributions in granular packings coming either from fluctuating density, velocity, elastic potential, or something yet not discovered.

This granular thermometer is an excellent tool for studying the dynamics of granular materials experimentally. As analytical and numerical evidence of the importance of the granular temperature mounts, there is a growing need for experimental validation of these concepts, and this technique provides a robust method for the quantification of the flow kinematics for systems with arbitrary geometry and grains.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary material 1 (DOCX 24045 kb)

Supporting information appendix (SI)

1.1 Appendix 1: Coarse-graining in cylindrical coordinates

Coarse-graining is an established technique for converting discrete particle measurements to continuum fields (see e.g.[45, 49, 50]). However, it is usually employed in Cartesian coordinate systems, whereas the experimental configuration of this paper is better suited to cylindrical coordinates $\varvec{r}=(r,\theta ,z)$, as shown in Fig. 7. We therefore outline below the coarse-graining process and the resulting granular temperature measurements in cylindrical coordinates.

The calculation is based on the mathematical formulation in [45, 49, 50]. We first introduce the coarse-graining function ${\mathcal {W}}$,

$$\begin{aligned} {\mathcal {W}}({\mathbf {r}}) = \frac{1}{2\pi \sigma _{r} \sigma _{z}}\exp {\left( -\frac{r^{2}}{2\sigma _{r}^{2}}-\frac{z^{2}}{2\sigma _{z}^{2}}\right) }, \end{aligned}$$

(11)

where $\sigma _{r}$ and $\sigma _z$ are the coarse-graining widths in the radial and vertical directions, respectively. Note the lack of $\theta$ dependence in (11), because we are interested in temperature fields only in the (r, z) half plane (and also independent of time). The normalisation is chosen to ensure that the coarse-graining function integrates to 1, i.e.

$$\begin{aligned} \iiint _{V} {\mathcal {W}}({\mathbf {r}})r\ dr\ dz\ d\theta = 1. \end{aligned}$$

(12)

It is then possible to define the coarse-grained solid volume $V(\varvec{r})$ as

$$\begin{aligned} V({\mathbf {r}})&= \sum _{k=1}^n\sum _{i \in S} \frac{\pi }{6} d_{i}^3 {\mathcal {W}}({\mathbf {r}}-{\mathbf {r}}_{i}(t_k)), \end{aligned}$$

(13)

where $\varvec{r}_{i}(t_k)$ represents the position of particle i at time $t_{k}$, and $d_{i}$ is the diameter of particle i. The sum $i\in S$ represents summing over all particles, and $k=1$ to n summing over n time steps.

We can then use this coarse-grained volume to obtain the steady-state average velocity field in the rz half-plane. For the radial component, the velocity $v_{r}(\varvec{r})$ is given by

$$\begin{aligned} v_{r} ({\mathbf {r}}) = \frac{1}{V(\varvec{r})}\displaystyle \sum _{k=1}^{n}\sum _{i \in S} \frac{\pi }{6} d_{i}^{3} {\mathcal {W}}({\mathbf {r}}-{\mathbf {r}}_{i}(t_k))v_{r,i}\left( t_{k}\right) , \end{aligned}$$

(14)

where $v_{r,i}(t_k)$ is particle i radial velocity at time $t_k$. This is calculated by converting the Cartesian positions from the tracking algorithm to cylindrical coordinates and then calculating the corresponding velocities. In a similar fashion, we can calculate an approximation of the square of the radial velocity as

$$\begin{aligned} v_{r}^{sq} ({\mathbf {r}}) = \frac{1}{V(\varvec{r})}\sum _{k=1}^{n}\sum _{i \in S} \frac{\pi }{6} d_{i}^{3} {\mathcal {W}}({\mathbf {r}}-{\mathbf {r}}_{i}(t_k))v_{r,i}^2(t_k). \end{aligned}$$

(15)

By definition, the granular temperature $T_{g}$ is the trace of the velocity variance tensor, in which the diagonal components are the variances of the average velocity of each component. $T_{g} = \frac{1}{3}(T_{g,r} + T_{g,\theta } + T_{g,z}) = \frac{1}{3}({\mathrm {Var}}(v_{r}) + {\mathrm {Var}}(v_\theta ) + {\mathrm {Var}}(v_z))$. Because the granular temperature of each component is the variance of the velocity field, we can define the coarse-grained granular temperature in the radial direction as

$$\begin{aligned} T_{g,r}({\mathbf {r}})= v_{r}^{sq} ({\mathbf {r}}) - (v_{r} ({\mathbf {r}}))^2. \end{aligned}$$

(16)

Analogously, components $T_{g,\theta }$ and $T_{g,z}$ are calculated by substituting the relevant velocity terms.

1.2 Appendix 2: Missed collisions

Sampling particle locations at discrete times necessarily means that not all collisions are observed. To account for this, we begin by considering the definition of the diffusivity, D, where if there is no net movement of the material, we have

$$\begin{aligned} D = \frac{{\mathbb {E}}[\Delta { x}^{2}]}{2\Delta { t}}, \end{aligned}$$

(17)

where ${\mathbb {E}}[\Delta x^2]$ is the mean square displacement of a large number of grains after a time $\Delta { t}$. For the case of uniform shear in the x direction, it has been shown [51] that the effect of the shear is to change this relationship to

$$\begin{aligned} D \propto \frac{{\mathbb {E}}[\Delta { x}^{2}]}{2\Delta { t}^{3/2}}. \end{aligned}$$

(18)

The constant of proportionality must therefore have the units of square root of time. For convenience, we assume that this time scales with the shear time, $|\dot{\gamma }|^{-1}$, so that we can write

$$\begin{aligned} D = \sqrt{a_{1}}\frac{{\mathbb {E}}[\Delta { x}^{2}]}{2\Delta { t}^{3/2}\sqrt{|\dot{\gamma }|}}, \end{aligned}$$

(19)

where $a_{1}$ is a non-dimensional fitting parameter. Recalling (6), we can define the measured granular temperature as

$$\begin{aligned} \widetilde{T}_{g} = \frac{1}{3}{\mathbb {E}}[||\varvec{v}'||^2] = \frac{1}{3}\frac{{\mathbb {E}}[\Delta x^2]}{\Delta { t}^2}. \end{aligned}$$

(20)

Substituting (19) in (20) gives

$$\begin{aligned} \widetilde{T}_{g} = \frac{2D}{3\sqrt{a_{1}\Delta { t}/|\dot{\gamma }|}}. \end{aligned}$$

(21)

Additionally, we can include some recent micromechanical measurements of $T_{g}$ [52] and D [4, 53], which give at steady state

$$\begin{aligned}&T_{g} \propto d|\dot{\gamma }|\sqrt{P/\rho }, \end{aligned}$$

(22)

$$\begin{aligned}&D \propto d^2|\dot{\gamma }|/\sqrt{I}, \end{aligned}$$

(23)

where d is the particle diameter, P the pressure, $\rho$ the particle density and $I=\dot{\gamma }d\sqrt{\rho /P}$ is the inertial number. From these, we can deduce that

$$\begin{aligned} \frac{T_{g}}{D} \propto \frac{|\dot{\gamma }|}{\sqrt{I}}. \end{aligned}$$

(24)

Substituting this relationship in (21) gives

$$\begin{aligned} \frac{T_{g}}{\widetilde{T}_{g}} \propto \frac{3}{2} \sqrt{a_{1}\frac{\Delta { t}}{t_{i}}}, \end{aligned}$$

(25)

where $t_{i}=d\sqrt{\rho /P}$ is the inertial time. We choose to replace the proportionality with an equality by assuming a translation of the curve in $\Delta { t}$ for the amount of $t_{0}$, rather than a strict proportionality, such that

$$\begin{aligned} \frac{T_{g}}{\widetilde{T}_{g}} = \frac{3}{2}\sqrt{\frac{a_{1}(\Delta { t} + t_{0})}{t_{i}}}. \end{aligned}$$

(26)

When $\Delta { t}=0$ we must have that $\widetilde{T}_{g} = T_{g}$, which yields $t_{0}$, and so by substituting $t_{0}$ this scaling becomes

$$\begin{aligned} \frac{T_{g}}{\widetilde{T}_{g}} = \alpha = \sqrt{a_{1}\frac{9}{4}\frac{\Delta { t}}{t_{i}} + 1}, \end{aligned}$$

(27)

In Fig. 5 we show a best fit of the parameter $a_{1}$ for the DEM data described in Sect. 4.

1.3 Appendix 3: Finite pixel size

Due to the finite size of the pixels on the detector panels, tracer positions cannot, even in principle, be measured perfectly, and thus every measured tracer position bears some randomness. The mathematical treatment of this randomness was developed in [48], and is reproduced here for clarity. The measured location of the particle centroid along the x axis, $\widetilde{x}$, differs from the true particle centroid x by a factor

$$\begin{aligned} \widetilde{x} = x + \tfrac{1}{2}p\xi , \end{aligned}$$

(28)

where p is the pixel size in meters, with $p=0$ representing perfect resolution, and $\xi$ is a random variable uniformly distributed in the domain $[-1, 1]$. The measured component of the tracer’s velocity in the x direction between two frames labelled 0 and 1 is then

$$\begin{aligned} \widetilde{v}_{x} = \frac{\widetilde{x}_{1} - \widetilde{x}_{0}}{\Delta { t}} = \frac{x_{1} - x_{0}}{\Delta { t}} + \frac{p(\xi _{1} - \xi _{0})}{2\Delta {t}} , \end{aligned}$$

(29)

where $v_{x}$ is the finite difference to the actual velocity and distribution of $\xi _{1} - \xi _{0}$ can be calculated by using the equation for compound probability density functions, as shown in [48]. Using this distribution the bias in the measured average velocity ${\mathbb {E}}[\widetilde{v}_{x}]$ is

$$\begin{aligned} {\mathbb {E}}[\widetilde{v}_{x}] = {\mathbb {E}}[v_{x}] + \frac{p}{2\Delta { t}}{\mathbb {E}}[\xi _{1} - \xi _{0}] = {\mathbb {E}}[v_{x}], \end{aligned}$$

(30)

since the expectation value of $\xi _{1} - \xi _{0}$ is 0, and hence no bias is introduced to the measurement of the average velocity. Nevertheless, $\xi _{1} - \xi _{0}$ introduces an uncertainty on the average velocity which is equal to one standard deviation of its distribution function, $\sigma _{\xi _{1} - \xi _{0}}$. Therefore the measured average velocity can be expressed as

$$\begin{aligned} {\mathbb {E}}[\widetilde{v}_x] = {\mathbb {E}}[v_x] \pm \frac{p}{2\Delta { t}}\sqrt{\tfrac{2}{3} - {\mathrm {Cov}}\left( \xi _{1}, \xi _{0} \right) }. \end{aligned}$$

(31)

The resulting error in the measured granular temperature component $\widetilde{T}_{g}$ in the x direction is

$$\begin{aligned} \widetilde{T}_{g_{xx}} = T_{g_{xx}} + \left( \frac{p}{2\Delta { t}}\right) ^{2}\left( {\mathrm {Var}}(\xi _{1}) + {\mathrm {Var}}(\xi _{0}) - {\mathrm {Cov}}\left( \xi _{1}, \xi _{0} \right) \right) , \end{aligned}$$

(32)

which, in the case that $\xi _{1}$ and $\xi _{0}$ are independent, simplifies to

$$\begin{aligned} \widetilde{T}_{g_{xx}} = T_{g_{xx}} + \frac{1}{6}\left( \frac{p}{\Delta { t}}\right) ^2. \end{aligned}$$

(33)

Because this bias is isotropic, we can additionally state that the overall granular temperature term can be expressed as

$$\begin{aligned}&\widetilde{T}_{g} = T_{g} + \Delta T_{g}^{\mathrm {res}}, \end{aligned}$$

(34)

$$\begin{aligned}&\Delta T_{g}^{\mathrm {res}} = \frac{1}{6}\left( \frac{p}{\Delta { t}}\right) ^{2}. \end{aligned}$$

(35)

1.4 Appendix 4: Absorption heterogeneity

The nature of granular materials is that they are generally heterogeneous at the particle scale. Because of this, radiographs of granular materials at this scale typically show heterogeneous absorption patterns, allowing us to observe the internal packing structure. This heterogeneity, however, introduces uncertainties in our measure of the particle centroids, as our definition of the tracer particle being the darkest disk in the image is only true for a homogeneous background.

Fig. 9

Example of a tracer in an artificial radiograph. The tracer is located at the centre of the image, and due to its high attenuation coefficient is the darkest region in the image. The heterogeneous background within intruder’s boundary causes skewing of intruder’s center towards the darker regions; right of intruder’s true centre in this case. The bulk particles are 15 cm (50 diameters) deep

In a dense granular packing, the effect of the heterogeneity on the accuracy of the tracer tracking algorithm depends on; (a) the particle size, (b) the number of bulk particles along the ray path, (c) the granular packing, and (d) the relative attenuation coefficient of the two materials. Here, we limit ourselves to tracers of the same size as the bulk particles, and to a single relative attenuation coefficient typical of a steel tracer in a glass medium. In this case, to approximate the error associated with the heterogeneity we have generated a series of high resolution (400 px/mm, chosen to eliminate detector resolution dependence from this analysis) artificial radiographs from DEM simulation data. Each radiograph represents a different thickness of glass beads along the path of the X-ray beam, and a single identical steel tracer is placed in front of each configuration. An example of these radiographs is shown in Fig. 9, with the tracer particle at the centre of the image.

For 25 different thicknesses, ranging from $n=H/d=1$ to 80 particle diameters deep, a tracer particle was placed at a known location and then the tracking algorithm was used to search for the particle location. This was repeated for 10,000 tracer locations uniformly distributed on a $100\times 100$ grid in each radiograph, and the error between the true location and the measured location was fitted with a zero mean Laplace distribution with non-dimensional width b (non-dimensionalised by the particle diameter). The Laplace probability density function (PDF) as a function of the fraction of the intruder diameter is given by

$$\begin{aligned} f(\chi ) = \frac{1}{2b}{\mathrm {e}}^{-\frac{|\chi |}{b}}, \end{aligned}$$

(36)

where $\chi$ is the normalized distance in the horizontal direction measured from the tracer’s center, and b is the non-dimensional width of the Laplace distribution calculated as a fitting parameter for each depth of bulk material. The dependence of this width on the packing depth is shown in Fig. 10 and can be well fitted by

$$\begin{aligned}&b\left( n\right) =a_2(1-{\mathrm {e}}^{-a_3\frac{H}{d}}), \end{aligned}$$

(37)

with coefficients $a_2=0.0048$ and $a_3=6.8\times 10^{-5}$. The width of the distribution and consequently the bias in the granular temperature asymptotically progresses towards a stable value with increasing bulk particle depth. This suggests that, in an ideal scenario, intruders are always visible even for a very large number of particles in front of them. In reality, however, with increasing depth of bulk particles it becomes more difficult to find the intruder due to the finite dynamic range of the detector panels, which prevent the detection of slight differences in the intensity of pixels.

Fig. 10

Estimating the effect of heterogeneity. Width of Laplace distribution b, in terms of intruder diameter fraction, plotted against number of particle layers in front of the tracer particle. Insets—histogram of error in measurement of position and line of fitted Laplace distribution for different bulk particle depths a $H/d=10/3$ and b $H/d=250/3$

To calculate the error caused by this heterogeneity we follow a similar logic to that in SI 1. The measured coordinate of the tracer can be expressed as the sum of the true value and a discrete random variable $\chi$ multiplied by the diameter of intruder d, as

$$\begin{aligned} \widetilde{x} = x + d\chi , \end{aligned}$$

(38)

where $\chi$ is distributed as in (36). It follows that the tracer’s x velocity component is given by

$$\begin{aligned} \widetilde{v}_x = \frac{\widetilde{x}_{1} - \widetilde{x}_{0}}{\Delta { t}} = \frac{x_{1} - x_{0}}{\Delta { t}} + d\frac{(\chi _{1} - \chi _{0})}{\Delta { t}} = v_{x} + \frac{d}{\Delta { t}}(\chi _{1} - \chi _{0}), \end{aligned}$$

(39)

The compound distribution function of the difference of $\chi _{1}$ and $\chi _{0}$ is symmetric around its zero mean, and does not introduce bias to the measured average velocity field, but introduces the uncertainty

$$\begin{aligned} {\mathbb {E}}[\widetilde{v}_{x}] = {\mathbb {E}}[v_{x}] \pm \frac{d}{\Delta { t}}\sqrt{(\mathrm {Var}(\chi _{1} - \chi _{0}) - 2\mathrm {Cov}(\chi _{1}, \chi _{0}))}. \end{aligned}$$

(40)

The expression for the x component of the measured granular temperature is

$$\begin{aligned}&\widetilde{T}_{xx} = T_{xx} + \Delta T_{xx}^{\mathrm {het}}\end{aligned}$$

(41)

$$\begin{aligned}&\Delta T_{xx}^{\mathrm {het}} = \left( \frac{d}{\Delta { t}}\right) ^2( {\mathrm {Var}}(\chi _{1} - \chi _{0}) - 2\mathrm {Cov}(\chi _{1}, \chi _{0})) \end{aligned}$$

(42)

The effect of this term on the measured temperature field is therefore strongly dependent on the independence of $\chi _{0}$ and $\chi _{1}$. In the case where they are independent (i.e. long sampling times relative to the particle displacement), the covariance approaches zero resulting in the maximum value of bias.

For short sampling times relative to the particle displacement, where the covariance of the two terms can be assumed to be close to the value of the variance, the bias caused by heterogeneity tends towards zero. In the cases reported here, we have assumed that the covariance and variance terms are equal in magnitude due to the short sampling times and similar background conditions in subsequent radiographs and have therefore ignored this error term.

1.5 Appendix 5: Finite sample size

Here we investigate the effect of using the finite sums (4) and (5) to approximate the true mean and variance (equivalently granular temperature) of the velocity field. For completeness, we redefine these estimators below

$$\begin{aligned} \widetilde{\mu }&= \frac{1}{N}\sum _{k=1}^{N} {v}_{k}, \end{aligned}$$

(43)

$$\begin{aligned} \widetilde{T}_{g}&= \frac{1}{N}\sum _{k=1}^{N} ({v}_{k}-\widetilde{\mu })^{2}, \end{aligned}$$

(44)

where it is now assumed that the true velocity measurements $v_{k}$ are used, so that we can study the finite sample size errors in isolation. Assuming these measurements are independent, it is straightforward to show that

$$\begin{aligned} {\mathbb {E}}[\widetilde{\mu }]&= {\mathbb {E}}[v], \end{aligned}$$

(45)

and

$$\begin{aligned} {\mathbb {E}}[\widetilde{T}_{g}]&= \frac{N-1}{N}\left( {\mathbb {E}}[v^{2}]-({\mathbb {E}}[v])^{2}\right) = T_{g} - \frac{1}{N}T_{g}. \end{aligned}$$

(46)

Hence the estimator for $T_{g}$ will, on average, underestimate the true granular temperature by $(1/N)T_{g}$.

Since the number of observations is typically large for the DEM simulation ($N>1000$), this bias can safely be neglected, although may start to become significant when fewer measurements are available.

1.6 Appendix 6: Measuring bulk temperature

Equipartition of energy is known to break down in agitated granular materials [54]. This means that we do not expect our tracer particle to have the same kinetic energy as the materials surrounding it. The kinetic energy in these systems is primarily dissipated through the contacts between grains. Any tracer particle which changes the local contact network may therefore affect the local temperature and bias any measurement. As a result, we do not expect the granular temperature of any tracer particles to be a true measure of the granular medium that would exist in the absence of the tracer particle. Whilst the relationship between the intruder and bulk temperatures are not known, and are the subject of intense research activity [1, 44, 55, 56], we here use DEM simulations to calculate the correction required for a system under simple shear, and use this value to correct our experimental data. In general, we expect this relationship to depend on at least the size, stiffness, density and friction ratios between the bulk and intruder particles.

The DEM simulation performed here is composed of a 3D Lees-Edwards boundary, of dimension $15\times 15\times 15$ mean bulk particle diameters, and sheared at constant volume within a 20% margin of the same bulk nominal values as in Table 1. For this case, we require that the contacts between grains are accounted for with realistic accuracy, and so choose to use a Hertz-Mindlin contact law [57, 58], with reduced glass bead and steel elastic modulii of 10 MPa and 30 MPa, particle densities of each material 2500 and 8000 kg/m$^3$, restitution coefficient of 0.95 and friction coefficient 0.5. The domain is filled with bulk particles of diameter $3\pm 0.3~\hbox {mm}$, with a single tracer particle, such that the total solid fraction is 0.596, which is chosen to achieve the target pressure. For this case, we find that the steel tracer particle has a lower temperature than the bulk particles by a factor of 1.5, and so the values reported in this paper could be divided by this value to recover the granular temperature of the glass beads.

1.7 Video 1

Caption: An overview of how X-ray radiography is used to measure the granular temperature for a vibro-fluidised bed.