Symmetry reduction in CSP model checking

Abstract

We present an extension of FDR, the model checker for the process algebra CSP, that exploits symmetry to reduce the size of the state space searched. We define what it means for a process to be symmetric with respect to a group of permutations on the transition labels. We factor the state space of the search by symmetry equivalence, mapping each state to a representative of its equivalence class, thereby considering all symmetric states together. We prove a powerful syntactic result, identifying conditions under which a process will be symmetric in a particular type. We show how to implement such a search using the powerful technique of supercombinators used in the implementation of FDR: we identify conditions on a supercombinator for it to be symmetric and explain how to apply a permutation to a state. Finally, we present a novel efficient technique for calculating representatives of equivalence classes, which normally finds unique representatives; our experiments suggest that this technique typically works faster than other techniques and in particular scales better.

1 Introduction

FDR [14] is a powerful model checker for the process algebra CSP [35]. FDR takes a list of CSP processes, written in machine-readable CSP (henceforth $\hbox {CSP}_M$); it can check whether one process refines another according to the CSP denotational models (e.g. the traces, failures and failures–divergences models), or it can check other properties, including deadlock freedom, livelock freedom and determinism. FDR has been widely used both within industry and in academia for verifying systems [13, 24, 33]. It is also used as a verification back end for several other tools including: Casper [27] which verifies security protocols; SVA [36] which can verify simple shared-variable programs; and several industrial tools (e.g. ModelWorks and ASD). The last few years have seen significant advances in FDR, leading to FDR3 [14] and FDR4, exploiting multi-core algorithms and using more efficient internal representations of processes, and also supporting large compute clusters; these advances have made a step change in the class of systems that can be analysed.

Many systems that one might want to model check contain symmetries. In this paper, we present an extension of FDR4 that exploits these symmetries: this gives considerable speed-ups in model checking (see Table 1); more importantly, we can now check much larger systems, including systems that, without symmetry reduction, would have well over $10^{26}$ states and so would be too large to check (on the same architecture) by a factor of more than $10^{16}$. Symmetry reduction has been applied previously in other model checkers: we give a review in Sect. 1.3.

Our main interest in symmetry reduction arises from our analysis of concurrent datatypes, particularly those based on linked lists [28]. Here, each node in the linked list is modelled by a CSP process, say of the form Node(me, datum, next), where me is the node’s identity, datum is some piece of data, and next is the identity of the next node in the list or a special value Null. Threads that operate on these nodes are also modelled as CSP processes. One can then analyse a system with some number n of nodes and some number t of threads. Clearly, a list of a particular length l can be formed in $n!/(n-l)!$ different ways by using different nodes, but all such states that correspond to the same sequence of datum values are symmetric. Further, different states can be symmetric in the type of the datums: for example, a list holding the sequence $\langle A,B,A\rangle$ is symmetric to one holding $\langle B,C,B\rangle$, say. Finally, the system is symmetric in the type of the thread identities.

Our approach is also applicable to network communication protocols in a dynamic network, where links may be broken or re-made, or where hosts may choose to use a particular sub-network for communication. Here the system is symmetric in the identities of hosts: different states of the network may be symmetric under permutations of these identities.

In general, our technique applies to systems that are fully symmetric in a particular type; however, we sketch (in Sect. 8) an example based on a ring of processes to show that, nevertheless, it can be applied to systems with a restricted form of symmetry.

We describe relevant background and formalise our notion of symmetry in Sect. 2: we define what it means for a labelled transition system (LTS) to be symmetric with respect to a group G of permutations on the labels of transitions and for a pair of states to be related under a permutation $\pi \in G$ ($\pi$-bisimilar).

By verifying the behaviour of the system from one state, we can deduce its correctness in all symmetric states. In Sect. 3 we present the idea behind the symmetry reduction. We map each state to a representative member of its (G-bisimilarity) equivalence class. FDR performs model checking by searching in the product automaton formed from the LTSs for the specification and implementation processes. We show how to perform a symmetry reduction on this product automaton and how to exploit this in a model checking algorithm. Our approach assumes only that the initial states of the specification and implementation processes are symmetric with respect to some group G of permutations (Definition 11); this contrasts with several other approaches which assume that every state of the specification is G-symmetric.

In Sect. 4 we consider how to identify syntactically that a system is symmetric in particular types $T_1,\ldots ,T_N$. We make certain assumptions about the CSP script principally that the script uses no constants of the relevant types. We show that the set of values associated with each channel or datatype constructor is invariant under permutations on each of $T_1,\ldots ,T_N$. Further, we show that—for any $\hbox {CSP}_M$ expression e, any environment $\rho$ giving values to free variables, and any permutation $\pi$—evaluating e in $\rho$ and then applying $\pi$ gives the same result as first applying $\pi$ to the values in $\rho$ and then evaluating e: we denote this $\pi (\mathsf{eval}\rho ~e) = \mathsf{eval}(\pi \mathbin {\scriptstyle \circ }\rho )~e$. In particular, this means that in the initial environment $\rho _1$,  $\pi (\mathsf{eval}\rho _1~e) = \mathsf{eval}\rho _1~e$ (since $\pi \mathbin {\scriptstyle \circ }\rho _1 = \rho _1$), and hence that the semantics of each process is symmetric under $\pi$. $\hbox {CSP}_M$ includes, as a sub-language, a lazy functional language, roughly equivalent to Haskell without type classes, but with the addition of sets, mappings and associative concatenation (“dot”). This sub-language is very convenient for modelling complex data, but considerably complicates reasoning about the full language.

Internally, FDR represents an LTS by a supercombinator, consisting of LTSs for component processes, with rules describing how component transitions are combined. Supercombinators are a powerful and efficient technique for modelling LTSs. They are generally applicable for modelling systems built from a number of components. In Sect. 5 we describe supercombinators and identify conditions on a supercombinator under which the corresponding LTS is symmetric.

In Sect. 6 we build on the syntactic result of Sect. 4. We show how to identify symmetries within a supercombinator. We then show how to apply a particular permutation to a state of the supercombinator.

In Sect. 7 we describe a way to calculate representative members of equivalence classes. This is believed to be a difficult problem, in general [6]. Our technique does not always give unique representatives (although nearly always does), but allows representatives to be calculated efficiently. Our approach works well in practice.

In Sect. 8 we report the results of experiments using our extension. The experiments show that the symmetry reduction provides considerable speed-ups in model checking; further, it allows us to analyse much larger systems than would otherwise have been possible. We also compare experimentally our technique for finding representative members of equivalence classes with two existing techniques; our results suggest that our approach is typically faster and in particular scales better.

We conclude in Sect. 9.

In the interests of exposition, we slightly simplify some aspects in the body of the paper and concentrate on the main ideas. In particular, in the body we restrict to the traces model of CSP; the stable failures and failures–divergences models (which require a different automaton for the specification) are dealt with in “Appendix B”; these require a generalisation of LTSs, which we present in “Appendix A”. Further, in the body we give a simplified version of supercombinators; full supercombinators are described in “Appendix C”, and symmetry techniques over them are described in “Appendix D”. In the interest of space, we omit some straightforward proofs; these can be found in [15].

Our main contributions, then, are:

• The identification of general syntactic conditions under which a system will be symmetric, based on a powerful language supporting complex datatypes;

• A general technique for finding representative members of equivalence classes for systems built from components, which seems to perform better than previous techniques;

• The adaptation of symmetry reduction to model checking based upon the powerful technique of supercombinators, in a way that makes fewer assumptions about the specification than some previous approaches; and

• The implementation of these techniques in an easy-to-use way, within an industrial-strength model checker, giving informative counterexamples when refinements do not hold.

1.1 A brief overview of CSP

In this section we give a brief overview of the fragment of $\hbox {CSP}_M$ that we will use in this paper. (Our technique applies to the whole of $\hbox {CSP}_M$, but we omit here operators that we will not use in the paper.) For more details on CSP, see [35, 39].

CSP is a process algebra for describing programs or processes that interact with their environment by communication. A CSP script contains definitions of datatypes, values, functions, channels and processes and also contains assertions to be checked by FDR; we explain these in more detail below. Figure 1 contains a full script; we explain this in detail in the next section, but use it to illustrate particular points here. (Scripts are written in ASCII; the script in Fig. 1 has been pretty printed.)

User-defined types may be introduced using the keyword datatype. For example, line 2 of the script introduces a type NodeIDType that contains seven atomic values. Such types may contain nonatomic values. For example, the declaration

creates a type that contains all values of the form Just.x where x is an Int, and the distinguished value Nothing; note how values are constructed using the dot operator “.”. Such datatype declarations may be recursive. For example, the declaration

defines a type that is isomorphic to finite lists containing Ints.

$\hbox {CSP}_M$ contains, as a sub-language, a strongly typed functional language, similar to Haskell but without type classes, and with the addition of sets and mappings. Thus, a script may contain definitions of values and of functions. Line 3 of the script defines a value NodeId which is a set containing six values. (diff is the set difference function.) The following function returns the length of an element of the above IntList type.

Built-in functions of the functional sub-language are described in [39].

Processes communicate via atomic events. Events often involve passing values over channels; for example, the event c.3 represents the value 3 being passed on channel c. Channels may be declared using the keyword channel. For example, line 11 contains a declaration of a channel freeNode whose events are of the form freeNode.t.n for each $t \in \textsf {ThreadID}$ and $n \in \textsf {NodeID}$ (so 18 events in total). Each channel has a fixed type, but channels can be declared to pass arbitrary values (excluding processes).

The simplest process is STOP, which represents a deadlocked process that cannot communicate with its environment. The process $a \rightarrow P$ offers its environment the event a; if the event is performed, the process then acts like P. The process $c?x \rightarrow P$ is initially willing to input an arbitrary value v on channel c, i.e. it is willing to perform any event of the form c.v; it binds the variable x to the value v received and then acts like P (which may use x). For example, line 26 defines a simple process Lock that repeatedly will perform any event of the form lock.t for $t \in {\textsf {ThreadID}}$ and then performs the corresponding unlock.t event. The process $c!v \rightarrow P$ outputs value v on channel c. Inputs and outputs may be mixed within the same communication, for example, the construct getDatum?t!me!datum (line 16) indicates that the process is willing to perform any event of the form getDatum.t.me.datum for $t \in {\textsf {ThreadID}}$, but using the current values of me and datum (from the process’s parameters).

The process $P \Box Q$ can act like either P or Q, the choice being made by the environment: the environment is offered the choice between the initial events of P and Q. For example, the Top process (line 22 of Fig. 1) is willing to communicate on either the getTop or setTop channel. By contrast, may act like either P or Q, with the choice being made internally (i.e. nondeterministically), not under the control of the environment. The process ${\mathbf {\mathsf{{if}}}}\, b\, {\mathbf {\mathsf{{then}}}}\, P {\mathbf {\mathsf{{else}}}}\, Q$ represents a conditional. $b \& P$ is a guarded process that makes P available only if b is true; it is equivalent to ${\mathbf {\mathsf{{if}}}}\, b\, {\mathbf {\mathsf{{then}}}}\, P {\mathbf {\mathsf{{else}}}}\, STOP$.

The process SKIP terminates immediately, represented by the special event $\surd$. P; Q represents the sequential composition of P and Q: P is run, but when it terminates, Q is run.

The process P  [|A|] Q runs P and Q in parallel, synchronising on events from A. The process $P |||Q$ interleaves P and Q, i.e. runs them in parallel with no synchronisation. The process $P \ A$ acts like P, except the events from A are hidden, i.e. turned into internal $\tau$ events.

Each of the binary operators has a corresponding indexed operator. For example, (sometimes written as ) is an indexed nondeterministic choice, with the choice being made over the processes P(x) for x in X, and (sometimes written as ) is a parallel composition of the processes P(t) for $t \in T$, where each P(t) is given alphabet A(t), and processes synchronise on events in the intersection of their alphabets.

CSP can be given an operational semantics in terms of labelled transition systems. From this, a denotational semantics can be defined. (Alternatively, the denotational semantics can be defined directly over the syntax, compositionally [35].) We describe these formally in Sect. 2 and Appendix A.

The simplest denotational model is the traces model. A trace of a process is a sequence of (visible) events that a process can perform. We say that P is refined by Q in the traces model, written $P \sqsubseteq _T Q$, if every trace of Q is also a trace of P. FDR can test such refinements automatically, for finite-state processes. Typically, P is a specification process, describing what traces are acceptable; this test checks whether Q has only such acceptable traces. Refinement assertions are written in $\hbox {CSP}_M$ scripts using the assert keyword (e.g. line 49).

FDR supports various compression functions that can be applied to processes. Most of these transform the labelled transition system in a way that preserves the denotational semantics, but normally gives a transition system with fewer states, so as to make model checking faster. (Some compression functions do not preserve the denotational semantics and are designed for special-purpose checks.)

1.2 A running example

We introduce here a running example, which we use to illustrate some of our techniques. (Our main interest is in more sophisticated concurrent datatypes than this that aim to be lock-free and linearisable [17]; however, we choose a simpler example here.) The example is of a concurrent lock-based stack that uses a linked list of nodes. The CSP model is presented in Fig. 1. This particular model includes six nodes, four possible data values that can be stored, and three threads (lines 2–5), but these parameters can easily be changed.

Fig. 1

The running example

Each node is represented by a process that is initially free (FreeNode(me)), but may be initialised by a thread to hold a datum and a reference to another node (Node(me, datum, next)); subsequently, the datum or next reference may be read, or the node freed.

A variable holding the top of the stack is also represented by a process (Top(top)), where the top may be read or set. Likewise, the lock is represented by a process (Lock) which may be alternately locked and unlocked.

Finally, each thread is represented by a process (Thread(me)). A thread may perform a push by obtaining the lock, reading the top, initialising a node appropriately to reference the previous top, setting the top to reference the new node, signalling completion and releasing the lock. It may perform a pop by obtaining the lock and reading the top; if the top is Null, then it signals that the pop failed because the stack is empty, and releases the lock; otherwise, it obtains the node referenced by the top node, updates the top to reference it, reads the datum from the previous top, signals completion, frees the node and releases the lock.

The processes are combined in parallel (lines 41–45), with all events hidden except those signalling completion of operations (process System). Figure 2 gives an illustration of a state of the system.

Fig. 2

An illustration of a state of the system. Thread T1 is pushing node N2 onto the stack and is about to set the top variable to point to N2 (in the syntactic state $\rightarrow \ldots$). Each box in the figure represents a process. Each edge illustrates where a variable of one process holds the identity of another

The specification is that of a stack. This is captured by the process Spec(s) (lines 47–48); the sequence s represents the contents of the stack. In the state illustrated in Fig. 2, we would expect the specification process to be in state Spec(${\mathsf {<}}$C,B${\mathsf {>}}$).¹ If the stack is nonempty, the top element can be popped, and otherwise a pop may fail; if the stack is not full, an element can be pushed on. The refinement check (line 49) tests whether the system refines the specification, i.e. whether every trace of the system is allowed by the specification, meaning that each sequence of push and pop operations on the system satisfies the normal properties of a stack.

FDR can verify the refinement check. However, it is slow, taking about thirty minutes on a 16-core machine and exploring 7.8 billion states and 21.4 billion transitions. However, there is a lot of symmetry in the system: it is symmetric in the types Data of data and ThreadID of thread identities and the subtype NodeID of real node identities. (Note that it is not symmetric in the type NodeIDType, which includes NodeID, because Null is treated as a distinguished value.) In Fig. 2, applying any permutation to each of these types gives a state that is equivalent, in a sense that we will make formal later. Applying the symmetry reduction technique of this paper to this system, for these three types, reduces the number of states to 99 thousand and reduces the checking time to less than a second.

Note, in particular, that while the initial state of the specification is symmetric, it can evolve into a state where it is holding data, where it is not symmetric with respect to the type Data. This is in contrast to several other approaches to symmetry reduction which require every state of the specification to be symmetric.

1.3 Related work

There have been several previous works applying symmetry reduction to model checking. Excellent surveys appear in [31, 41].

Clarke et al. [6, 7] consider symmetry in the context of symbolic temporal logic model checking. They consider symmetries that permute components within system states; however, the permutations do not affect the values in shared variables, and so they do not capture all symmetries present when one process can hold the identity of another, as in our motivating example. They use the representative technique: they adapt the transition relation so as to produce representative members of each equivalence class of states, thereby factoring the transition system with respect to equivalence. They then show that, subject to certain restrictions, the specification $\phi$ (in $\hbox {CTL}^*$) is satisfied in the reduced transition system iff it is satisfied in the original system. More precisely, they require that equivalent states have the same set of propositional labels from $\phi$: this means that the specification cannot talk directly about symmetric values, which makes it more restrictive than our approach. They show that finding unique representatives, in general, is at least as hard as the graph isomorphism problem, which is widely accepted as being difficult (although not known to be NP-complete). They therefore adapt their technique to use representatives that might not be unique. Their approach requires the user to define how to choose representatives.

Emerson and Sistla [11] also consider symmetry in the context of temporal logic model checking. Their focus is on systems containing many identical or isomorphic components. They show how symmetry of the model can be deduced from symmetry of the system’s structure. As with [7], they factor the transition system with respect to equivalence and prove that the specification (in $\hbox {CTL}^*$ or Mu-Calculus) is satisfied in the reduced transition system iff it is satisfied in the original system. They allow the group actions to also operate on the labels of the state; however, they require that the group actions preserve certain significant sub-formulas of the specification, which makes their approach more restrictive than ours. In [12], the same authors extend their approach, so as to model check against a specification written in propositional linear temporal logic, relaxing the above condition, using an approach similar to ours.

Sistla et al. [38] describe a model checker, SMC, that builds on the ideas of [12]. In addition to factoring the transition system with respect to symmetric equivalence, they employ a second reduction strategy known as state symmetry: if there are several symmetric transitions from a particular state (so the successor states are symmetric), then only one such transition is expanded. (We leave the investigation of this reduction strategy within FDR as future work: it seems somewhat harder in our setting, because multiple processes synchronise on each transition.) They store previously seen states in a hash table using a hash function that respects symmetries. (So symmetric states are placed in the same bucket.) When a new state s is encountered, for every state $s'$ that hashes to the same value, the algorithm tries to test whether s and $s'$ are indeed symmetric (using an approximating algorithm that sometimes fails to identify symmetries).

Ip and Dill [19] investigate symmetry using the Mur$\phi$ model checker. They introduce the notion of a scalarset: effectively a type where all elements are treated equivalently: this is analogous to our symmetric types. They show that any Mur$\phi$ program using such scalarsets is symmetric in each scalarset. They then factor the transition system with respect to the symmetry relation, as with the previous papers. They restrict to certain simple correctness properties: error freedom and deadlock freedom.

Bošnački et al. [3] describe an extension to the Spin model checker to support symmetry, building on the techniques of [19]. They present several strategies for defining representative functions; we compare these with our own approach in Sects. 7 and 8.

The work closest to ours is that by Moffat et al. [32], who investigate the use of symmetry in CSP model checking. They introduce the notion of permutation bisimulations—informally, renaming transitions of an LTS according to some permutation on the events—which we adapt. They then factor the LTS according to the induced equivalence. They present structured machines—a restricted form of supercombinators—to represent CSP systems and present some algebraic rules that can be used to deduce symmetries between components. They then present a model checking algorithm based on these ideas, restricting the specification process to one such that every state is symmetric (in contrast to our approach). Our advances over this work are: a much more general technique for identifying symmetry; a more general form of representing processes (i.e. supercombinators), which scales far better; fewer restrictions on the type of specification process that can be used; an efficient, general representative choosing algorithm; and the incorporation of these techniques within an industrial-strength model checker.

Jensen [21] applies symmetry reduction to the state space of coloured Petri nets; correctness conditions are rather limited, in particular considering only properties that are fully symmetric. Chiola et al. [5] perform a similar reduction, but also factor the firings of the net according to symmetry. Schmidt [37] also studies symmetry reduction in the context of Petri nets. Junttila [22] studies the complexity of this problem.

Leuschel et al. [25] give an extension for ProB, a model checker for B, that uses symmetry reduction. This uses a different technique called permutation flooding where every symmetric permutation of a state is added to the set of visited states.

TopSPIN [9, 10] is an extension to SPIN that enables symmetry reduction on a wider variety of scripts than other approaches. Specifically, it allows processes to hold references to other processes (like we allow in this paper, but unlike [6], as discussed above). The authors show how to extend any algorithm used to find representatives when no process holds such references to an algorithm for when processes do hold references. The result is an exact algorithm that always finds a unique representative, but may take exponential time to do so.

2 Background

In this section we describe relevant background material concerning model checking. We describe how FDR represents CSP processes in terms of labelled transition systems (LTSs) and present some operations over those LTSs. We give here a slightly simplified description, in the interests of exposition. In particular, in the body of the paper we restrict to the traces model, which will mean that we can represent processes by labelled transition systems (Definition 1). In the appendices, we will generalise, so as to be able to consider the other semantic models; this will require a generalisation of labelled transition systems.

We also briefly review permutations and permutation groups and then formalise the notion of symmetry over LTSs.

2.1 Labelled transition systems

We assume a set of events $\varSigma$ with $\tau ,\surd \notin \varSigma$. Let ${\varSigma ^{\surd }}= \varSigma \cup \{\surd \}$ and ${\varSigma ^{\tau \surd }}= \varSigma \cup \{\surd ,\tau \}$. Let ${\varSigma ^{\surd }}^*$ denote all sequences of events from ${\varSigma ^{\surd }}$ such that $\surd$ occurs only as the last event (if at all); we call such a sequence a trace.

Definition 1

A labelled transition system (LTS) is a tuple $L = (S, \varDelta , init)$ where:

• S is a set of states;

• $\varDelta \subseteq S \times {\varSigma ^{\tau \surd }}\times S$ is a transition relation;

• $init\in S$ is the initial state.

In the remainder of this paper we restrict to connected LTSs, i.e. where every state is reachable from the initial state by zero or more transitions.

If $(s,a,s') \in \varDelta$, we write $s \xrightarrow {a} s'$ (we decorate the arrow with “L” if this is not implicit from the context); this indicates that the process from state s can perform the event a and move into state $s'$. We write $s \xrightarrow {a}$ iff $\exists s' \cdot s \xrightarrow {a} s'$. For $tr = a_1 \ldots a_n \in ({\varSigma ^{\tau \surd }})^*$, we write iff there exists $s_0, \ldots , s_n$ such that $s = s_0 \xrightarrow {a_1} s_1 \cdots s_{n-1} \xrightarrow {a_n} s_n = s'$. We write iff s can perform zero or more $\tau$-events to become $s'$. We sometimes write $s \in L$ to mean $s \in S$.

We can then define the traces of a state s of an LTS:²

If L is an LTS, we will write traces(L) for the traces of the initial state of L.

Let S and I be LTSs, representing a specification and implementation, respectively. We define refinement between S and I in the traces model of CSP as follows.

$$\begin{aligned} S \sqsubseteq _T I&iff&traces(S) \supseteq traces(I). \end{aligned}$$

FDR translates CSP processes into LTSs and then tests for the above refinement.

When FDR performs a refinement check of the form $Spec \sqsubseteq Impl$, it starts by normalising the specification Spec [35, Section 16.1]. We remind the reader of the definition of bisimilarity.

Definition 2

(Bisimilarity) Let $L_1 = (S_1, \varDelta _1, init_1)$, and $L_2 = (S_2, \varDelta _2, init_2)$ be LTSs. We say that $\mathord {\sim } \subseteq S_1 \times S_2$ is a bisimulation between$L_1$and$L_2$ iff whenever $(s_1, s_2) \in \mathord {\sim }$ and $a \in {\varSigma ^{\tau \surd }}$:

• If $s_1\xrightarrow {a} s_1'$ then $\exists s_2' \in S_2 \cdot s_2 \xrightarrow {a} s_2' \wedge s_1' \sim s_2'$;

• If $s_2 \xrightarrow {a} s_2'$ then $\exists s_1' \in S_1 \cdot s_1 \xrightarrow {a} s_1' \wedge s_1' \sim s_2'$.

We say that $s_1, s_2 \in S$ are bisimilar iff there exists a bisimulation relation $\sim$ such that $s_1 \sim s_2$.

In many cases (e.g. the Spec process from Fig. 1), normalisation leaves the specification unchanged. However, normalisation has an effect, in particular, when the specification contains nondeterminism: the critical property of the normalised process (Lemma 4) is that it reaches a unique state after each trace.

Definition 3

Given an LTS $L = (S, \varDelta , init)$, its prenormal form is an LTS³$N = ({\mathbf{P }S - \{\{\}\}}, \varDelta _N, init_N)$ defined as follows. Each state is a nonempty element of $\mathbf{P }S$. The initial state is , i.e. all states reachable (in L) from $init$ by zero or more $\tau$-transitions. For each state $\hat{s} \in \mathbf{P }S - \{\{\}\}$, and for each non-$\tau$ event a that can be performed by a member of ${\hat{s}}$, we include in $\varDelta _N$ an a-transition from ${\hat{s}}$ to , i.e. all states reached (in L) from s by an a-transition followed by zero or more $\tau$-transitions.

The normal form for L, denoted norm(L), is calculated by taking the prenormal form for L, restricting to reachable states and then factoring by strong bisimulation (i.e. compressing the LTS, combining bisimilar states). We say that an LTS is normalised if it is the normal form of some LTS.

Figure 3 gives an example.

Fig. 3

The LTS for the process (left) and its normal form (right)

Note that the normal form for a process has no $\tau$ transitions, no pair of transitions from the same state with the same label and no strongly bisimilar states. The following lemma shows that in a normalised LTS, the state reached after a particular trace is unique.

Lemma 4

If LTS $P = (S, \varDelta , init)$ is normalised, and and then $p = p'$.

Lemma 5

Let $N = norm(P)$. Then the traces of P and N are equal.

In order to check whether $P \sqsubseteq _T Q$, FDR explores the product automaton of P and Q.

Definition 6

Let $P = (S_P, \varDelta _P, init_P)$ be a normalised LTS, and $Q = (S_Q, \varDelta _Q, init_Q)$ be an LTS. The product automaton of P and Q is a tuple $(S, \varDelta , init)$ such that

• $S = S_P \times S_Q$;

• $((p, q), a, (p', q')) \in \varDelta$ iff $q \xrightarrow {a}_Q q'$, and if $a \ne \tau$ then $p \xrightarrow {a} p'$ else $p = p'$;

• $init= (init_P, init_Q)$.

Note that P contains no $\tau$ transitions, hence the asymmetry in the definition.

Example 7

Let channels l, m and r pass data from type $T = \{A,B\}$, and consider the processes

This represents two one-place buffers chained together. Its specification is a two-place buffer:

$$\begin{aligned} \begin{array}{rcl} P &{} = &{} l?x \rightarrow P'(x) \\ P'(x) &{} = &{} l?y \rightarrow P''(x,y) \Box r!x \rightarrow P \\ P''(x,y) &{} = &{} r!x \rightarrow P'(y). \end{array} \end{aligned}$$

The LTSs for Q, P (which is already normalised) and the product automaton are shown in Fig. 4.

Fig. 4

The LTSs for the processes from Example 7 and their product automaton. We write, for example, $L \parallel R$ as shorthand for

The following lemma relates sequences of transitions of the product automaton to sequences of transitions of the components.

Lemma 8

Suppose M is the product automaton of P and Q. Then

Further, $p_1$ is unique (for a given choice of tr).

2.2 Permutations

Let X be a set. A permutation on X is a bijection $\pi : X \rightarrow X$. We denote the inverse of a permutation $\pi$ by $\pi ^{-1}$. We write $\pi ;\pi '$ for the forward composition of $\pi$ and $\pi '$, and $\pi \mathbin {\scriptstyle \circ }\pi '$ for the backwards composition:

$$\begin{aligned} (\pi ;\pi ')(x) = (\pi ' \mathbin {\scriptstyle \circ }\pi )(x) = \pi '(\pi (x)). \end{aligned}$$

We let $id_X$ denote the identity permutation on X; we write this simply as id when the underlying set is clear from the context.

The set of all permutations of a set X forms a group under backwards composition, which we denote $Sym (X)$. In the Introduction, we mentioned permutations of the (sub-)types NodeID, Data and ThreadID from Fig. 1. If G is a group, then $G' \le G$ denotes that $G'$ is a subgroup of G.

Our main focus is on event permutations. However, we do not want to change the semantic events, $\surd$ and $\tau$. Thus, we let $EvSym \le Sym ({\varSigma ^{\tau \surd }})$ denote the largest symmetry subgroup such that for all permutations $\pi \in EvSym$,  $\pi (\tau ) = \tau$ and $\pi (\surd ) = \surd$. $\pi$ is an event permutation iff $\pi \in EvSym$.

We will often consider systems that are symmetric in one or more disjoint datatypes, say $T_1,\ldots ,T_n$; the system in the running example is symmetric in NodeID, Data and ThreadID. In this case, let $\pi _i \in Sym(T_i)$, for $i = 1,\ldots ,n$; then consider $\pi = \bigcup _{i=1}^n \pi _i$. We say that $\pi$ is type-preserving, since it maps elements of each $T_i$ onto $T_i$. Note that $\pi \in Sym(\bigcup _{i=1}^n T_i)$; further, the group of all such type-preserving permutations is isomorphic to the direct product of $Sym(t_1)$, ..., $Sym(t_n)$.

Given a type-preserving permutation $\pi$ on atomic values, $\pi$ can be lifted to events in ${\varSigma ^{\tau \surd }}$ by point-wise application; for example, $\pi (getDatum.t.n.d) = getDatum.\pi (t).\pi (n).\pi (d)$.

2.3 Symmetric LTSs

We now define what it means for an LTS to be symmetric. For this Sects. 3 and 5, we consider symmetries from an arbitrary event permutation group $G \le EvSym$. In later sections, we specialise the group to be formed from permutations on datatypes.

The following definition is adapted from [32].

Definition 9

(Permutation bisimilarity) Let $L_1 = (S_1, \varDelta _1, init_1)$, and $L_2 = (S_2, \varDelta _2, init_2)$ be LTSs, and let $\pi \in G$ be an event permutation. We say that $\mathord {\sim } \subseteq S_1 \times S_2$ is a $\pi$-bisimulation between$L_1$and$L_2$ iff whenever $(s_1, s_2) \in \mathord {\sim }$ and $a \in {\varSigma ^{\tau \surd }}$:

• If $s_1\xrightarrow {a} s_1'$ then $\exists s_2' \in S_2 \cdot s_2 \xrightarrow {\pi (a)} s_2' \wedge s_1' \sim s_2'$;

• If $s_2 \xrightarrow {a} s_2'$ then $\exists s_1' \in S_1 \cdot s_1 \xrightarrow {\pi ^{-1}(a)} s_1' \wedge s_1' \sim s_2'$.

We say that $s_1, s_2 \in S$ are $\pi$-bisimilar, denoted $s_1 \sim _\pi s_2$ iff there exists a $\pi$-bisimulation relation $\sim$ such that $s_1 \sim s_2$. We say that $L_1$ and $L_2$ are $\pi$-bisimilar, denoted $L_1 \sim _\pi L_2$, iff $init_1 \sim _\pi init_2$.

Note that the case $\pi = id$ corresponds to strong bisimulation.

For example, in Fig. 4, the states $P'(A)$ and $P'(B)$ (second column of the second LTS) are $\pi$-bisimilar, where $\pi (A) = B$ and $\pi (B) = A$. Further, the initial state of each LTS is $\pi$-bisimilar to itself, for every $\pi \in Sym(\{A,B\})$.

The following lemma follows immediately from the above definition.

Lemma 10

Let $\pi$ and $\pi '$ be event permutations.

• 1. If $s_1 \sim _\pi s_2$ then $s_2 \sim _{\pi ^{-1}} s_1$;

• 2. If $s_1 \sim _\pi s_2$ and $s_2 \sim _{\pi '} s_3$ then $s_1 \sim _{\pi ;\pi '} s_3$.

The techniques we present in the following sections will require the specification and implementation LTSs to be symmetric in the following sense.

Definition 11

Let L be an LTS and $\pi \in EvSym$ be an event permutation. We say that L is $\pi$-symmetric iff $L \sim _\pi L$. Let $G \le EvSym$. We say that L is G-symmetric iff for all $\pi \in G$, L is $\pi$-symmetric.

For example, each LTS in Fig. 4 is $Sym(\{A,B\})$-symmetric. Note that every LTS is $\{id\}$-symmetric.

Lemma 12

If L is $\pi$-symmetric then for every state s of L, there exists a state $s'$ in L such that $s \sim _\pi s'$.

3 Refinement checking on symmetric LTSs

In this section we present—at a fairly high level of abstraction—our refinement checking algorithms for the traces model. In Sect. 3.1 we consider relevant properties of the specification, in particular that normalising a symmetric specification LTS preserves symmetry. As noted in introduction, our basic approach is to map each state encountered in the search to a representative member of its G-equivalence class; we define such representatives in Sect. 3.2. In Sect. 3.3 we present the reduced product automaton, which is explored by the model checking algorithm, created by replacing each state by its representative; we then present relevant results about the reduced automaton. In Sect. 3.4, we translate the refinement relationship into a property of the product automaton and so present the model checking algorithm itself.

Fix an event permutation group $G \le EvSym$.

3.1 Symmetric normalised specifications

Recall that FDR normalises the specification before exploring the product automaton. We prove that symmetry is preserved by normalisation.

Lemma 13

If $P = (S_P,\varDelta _P,init_P)$ is a G-symmetric LTS, then norm(P) is a G-symmetric normalised LTS.

Proof

(sketch). Let $N = (S_N,\varDelta _N,init_N)$ be the prenormal form for P. Let $\pi \in G$, and suppose $\sim$ is a $\pi$-bisimulation over $S_P$. Define a corresponding relation $\approx$ over $S_N$ as follows:

$$\begin{aligned} \begin{aligned} N_1 \approx&N_2 \iff (\forall s_1 \in N_1 \cdot \exists s_2 \in N_2 \cdot s_1 \sim s_2) \\&\wedge (\forall s_2 \in N_2 \cdot \exists s_1 \in N_1 \cdot s_1 \sim s_2). \end{aligned} \end{aligned}$$

It is then straightforward to show that $\approx$ is a $\pi$-bisimulation [15]. Hence N is G-symmetric.

Clearly neither factoring by strong bisimulation nor removing unreachable states breaks G-symmetry. Hence norm(P) is G-symmetric. $\square$

We will need to apply permutations to states of the specification. The following lemma justifies the soundness of this.

Lemma 14

Let P be a G-symmetric normalised LTS. Then, for each $s\in P$ and $\pi \in G$, there exists a unique$s'\in P$ such that $s\sim _\pi s'$.

Proof

The existence of $s'$ follows directly from Lemma 12. In order to show $s'$ is unique, suppose $s \sim _\pi s''$. Then $s' \sim _{\pi ^{-1};\pi } s''$, i.e. $s' \sim _{id} s''$, that is, s and $s''$ are strongly bisimilar, so $s' = s''$ by definition of normalisation. $\square$

Definition 15

Let P be a G-symmetric normalised LTS, and let $s\in P$ and $\pi \in G$. Then, we write $\pi (s)$ for the unique $s'$, implied by the above lemma, such that $s\sim _\pi s'$.

3.2 Representative members

The following definition formalises the notion of a representative member of an equivalence class.

Definition 16

Let $L = (S, \varDelta , init)$ be a G-symmetric LTS. Write $s_1 \sim _G s_2$ iff there exists $\pi \in G$ such that $s_1 \sim _\pi s_2$. Note that $\sim _G$ is an equivalence relation.

We say that $rep : S \rightarrow S$ is a G-representative function forL if ${s \sim _G rep(s)}$ for every $s \in S$. We define $rep(S) = \{rep(s) \mid s \in S\}$, the set of representative states; we abuse notation and write rep(L) for the same set.

We say that rep gives unique representatives if $\forall s, s' \in S \cdot s \sim _G s' \implies rep(s) = rep(s')$, i.e. rep selects a unique representative of each equivalence class.

For the rest of this section, we assume the existence of a G-representative function rep for Q.

Ideally, we would like our representative functions to produce unique representatives, because this will give the greatest reduction in the state space. However, finding unique representatives is hard, in general [6]. Therefore, our approach will not assume this. Section 7 considers how to define a suitable efficient representative function that produces unique representatives in most cases.

3.3 The reduced product automata

We now show how to factor the product automaton using a G-representative function. Our subsequent model checking algorithm will search in this reduced product automaton.

Throughout this section, let $P = (S_P, \varDelta _P, init_P)$ be a normalised G-symmetric LTS, $Q = (S_Q, \varDelta _Q, init_Q)$ be a G-symmetric LTS, and rep be a G-representative function on Q.

Definition 17

We lift rep to pairs of states from $S_P \times S_Q$ by defining

$$\begin{aligned} \begin{aligned}&rep(p, q) = (\pi (p), rep(q)) \\&\quad \hbox { where } \pi \hbox { is such that } q \sim _\pi rep(q). \end{aligned} \end{aligned}$$

That is: we map q to its representative rep(q), and we map p according to a corresponding permutation $\pi$. (There may be several such $\pi$, in which case we choose an arbitrary one.) Below we use names like $(\hat{p}, \hat{q})$ for such representative pairs of states.

The rep-reduced product automaton of P and Q is a product automaton $(S_P \times rep(Q), \varDelta , init)$, such that

• $(\hat{p}, \hat{q}) \xrightarrow {a} rep(p',q')$ in $\varDelta$ if $\hat{q}\in rep(Q)$, and $(\hat{p}, \hat{q}) \xrightarrow {a} (p', q')$ in the standard product automaton of P and Q (i.e. $\hat{q}\xrightarrow {a}_Q q'$, and if $a \ne \tau$ then $\hat{p}\xrightarrow {a}_P p'$ else $\hat{p}= p'$).

• $init= rep(init_P, init_Q)$.

Example 18

Recall the processes from Example 7. The product automaton there has five equivalence classes for states. Figure 5 gives the reduced product automaton, based on a function rep that gives unique representatives.

Fig. 5

Reduced product automaton for the processes from Example 7

Throughout the rest of this section, let S be the standard product automaton of P and Q, and R the reduced product automaton of P and Q.

The following lemma, illustrated below, shows how steps of the standard product automaton are matched by steps of the reduced product automaton, and vice versa.

Lemma 19

• 1. If $(p_1, q_1) \xrightarrow {a}_S (p_2, q_2)$ and $q_1 \sim _\pi {\hat{q}}_1$ with ${\hat{q}}_1 \in rep(Q)$, then

  $$\begin{aligned} \begin{aligned}&\exists {\hat{q}}_2 \in rep(Q), \pi ' \in G \cdot \\&\qquad (\pi (p_1), \hat{q}_1) \xrightarrow {\pi (a)}_R (\pi '(p_2), \hat{q}_2) \wedge q_2 \sim _{\pi '} \hat{q}_2. \end{aligned} \end{aligned}$$

• 2. If $({\hat{p}}_1, \hat{q}_1) \xrightarrow {a}_R (\hat{p}_2, \hat{q}_2)$,  $q_1 \sim _\pi \hat{q}_1$ and $\hat{p}_1 = \pi (p_1)$, then

  $$\begin{aligned} \begin{aligned}&\exists p_2, q_2, \pi ' \cdot (p_1, q_1) \xrightarrow {\pi ^{-1}(a)}_S (p_2, q_2) \\&\qquad \wedge q_2 \sim _{\pi '} \hat{q}_2 \wedge \hat{p}_2 = \pi '(p_2). \end{aligned} \end{aligned}$$

Proof

• 1. Since $(p_1, q_1) \xrightarrow {a}_S (p_2, q_2)$ we have that $q_1 \xrightarrow {a}_Q q_2$. Then since ${q_1 \sim _\pi {\hat{q}}_1}$, there exists $q' \in S_Q$ such that $\hat{q}_1 \xrightarrow {\pi (a)}_Q q' \wedge {q_2 \sim _\pi q'}$. Let $\hat{q}_2 = rep(q')$ and $\pi ''$ be such that $q' \sim _{\pi ''} \hat{q}_2$. Then, $q_2 \sim _{\pi '} \hat{q}_2$ where $\pi ' = \pi ;\pi ''$.

  If $a \ne \tau$, then $p_1 \xrightarrow {a}_P p_2$ by the definition of S. Hence, $\pi (p_1) \xrightarrow {\pi (a)}_P \pi (p_2)$. So by the definition of R,  $(\pi (p_1), \hat{q}_1) \xrightarrow {\pi (a)}_R (\pi ''(\pi (p_2)), \hat{q}_2)$. But $\pi ''(\pi (p_2)) = \pi '(p_2)$, as required.

  The case $a = \tau$ is similar, except $p_1 = p_2$ and $\pi (p_1) = \pi (p_2)$.

• 2. From the definition of R, there exists $q_2'$ such that $\hat{q}_1 \xrightarrow {a}_Q q_2'$ and $\hat{q}_2 = rep(q_2')$. Then by the definition of $\sim _\pi$, there exists $q_2$ such that $q_1 \xrightarrow {\pi ^{-1}(a)}_Q q_2$ and $q_2 \sim _\pi q_2'$. Let $\pi ''$ be such that $q_2' \sim _{\pi ''} \hat{q}_2$. Then $q_2 \sim _{\pi '} \hat{q}_2$ where $\pi ' = \pi ;\pi ''$.

  If $a \ne \tau$, then by the definition of R, there exists $p_2'$ such that $\hat{p}_1 \xrightarrow {a}_P p_2'$ and $\hat{p}_2 = \pi ''(p_2')$. Then, since $\hat{p}_1 = \pi (p_1)$,  there exists $p_2$ such that $p_1 \xrightarrow {\pi ^{-1}(a)}_P p_2$ and $p_2' = \pi (p_2)$. Hence $\hat{p}_2 = \pi '(p_2)$. Then from the definition of S,  $(p_1, q_1) \xrightarrow {\pi ^{-1}(a)}_S (p_2, q_2)$.

  The case $a = \tau$ is similar, except $\hat{p}_1 = p_2'$ and $p_1 = p_2$.

$\square$

The following lemma shows that for every trace of the standard product automaton, there is a corresponding trace of the reduced product automaton, and vice versa.

Lemma 20

Let tr be a trace in ${\varSigma ^{\tau \surd }}^*$.

• 1. Suppose in the standard product automaton:

  

  Then in the reduced product automaton:

  

• 2. Suppose in the reduced product automaton:

  

  Then in the standard product automaton:

  

Proof

Both parts follow by a straightforward induction, making use of Lemma 19. More precisely, we can show the following.

• 1. If the standard product automaton has transitions as follows:

  $$\begin{aligned} \begin{aligned}&(p_0, q_0) \xrightarrow {a_0}_S (p_1, q_1) \xrightarrow {a_1}_S \ldots \xrightarrow {a_{n-1}}_S (p_n, q_n) \\&\quad \wedge q_0 \sim _{\pi _0} {\hat{q}}_0 \in rep(Q) . \end{aligned} \end{aligned}$$

  Then the reduced product automaton has transitions as follows:

  $$\begin{aligned} \begin{aligned}&(\pi _0(p_0), \hat{q}_0) \xrightarrow {\pi _0(a_0)}_R (\pi _1(p_1), \hat{q}_1) \xrightarrow {\pi _1(a_1)}_R \ldots \\&\qquad \qquad \xrightarrow {\pi _{n-1}(a_{n-1})}_R (\pi _n(p_n), \hat{q}_n)\wedge \\&\qquad \qquad \forall i \in \{0,\ldots ,n\} \cdot q_i \sim _{\pi _i} \hat{q}_i , \end{aligned} \end{aligned}$$

  for some ${\hat{q}}_1, \ldots , {\hat{q}}_n \in rep(Q)$,  $\pi _1, \ldots , \pi _n \in G$.

• 2. If the reduced product automaton has transitions as follows:

  $$\begin{aligned} \begin{aligned}&({\hat{p}}_0, \hat{q}_0) \xrightarrow {a_0}_R (\hat{p}_1, \hat{q}_1) \xrightarrow {a_1}_R \ldots \xrightarrow {a_{n-1}}_R (\hat{p}_n, \hat{q}_n) \\&\qquad \wedge q_0 \sim _{\pi _0} \hat{q}_0 \wedge \hat{p}_0 = \pi _0(p_0) . \end{aligned} \end{aligned}$$

  Then the standard product automaton has transitions as follows:

  $$\begin{aligned} \begin{aligned}&(p_0, q_0) \xrightarrow {\pi _0^{-1}(a_0)}_S (p_1, q_1) \xrightarrow {\pi _1^{-1}(a_1)}_S \ldots \\&\qquad \xrightarrow {\pi _{n-1}^{-1}(a_{n-1})}_S (p_n, q_n)\wedge \\&\qquad \qquad \forall i \in \{0,\ldots ,n\} \cdot q_i \sim _{\pi _i} \hat{q}_i \wedge \hat{p}_i = \pi _i(p_i). \end{aligned} \end{aligned}$$

  for some $p_1, \ldots , p_n \in S_P$,  $q_1, \ldots , q_n \in S_Q$,  $\pi _1, \ldots , \pi _n \in G$.$\square$

3.4 Refinement checking algorithm for the traces model

We now present the model checking algorithm for the traces model. Throughout this section, let $P = (S_P, \varDelta _P, init_P)$ be a normalised G-symmetric LTS, $Q = (S_Q, \varDelta _Q, init_Q)$ be a G-symmetric LTS, rep be a G-representative function on Q, S be the standard product automaton of P and Q, and R be the reduced product automaton of P and Q.

The following proposition shows how trace refinements are exhibited in the reduced product automaton.

Proposition 21

$P \sqsubseteq _T Q$ iff

Fig. 6

Traces-refinement model checking algorithm on the reduced product automaton

Proof

($\Rightarrow$) We prove the contrapositive. Suppose

Then by Lemma 20, there exist a trace $tr'$, states p and q, and $\pi \in G$ such that

Also, since $\hat{q}\xrightarrow {a}_Q$ and , we have Hence⁴$(tr' \ \tau ) \frown \langle \pi ^{-1}(a)\rangle \in traces(init_Q)$, but (by the uniqueness of the state p reached after $tr'$, Lemma 4) $(tr' \ \tau ) \frown \langle \pi ^{-1}(a)\rangle \notin traces(init_P)$. Hence $P \not \sqsubseteq _T Q$.

($\Leftarrow$) We prove the contrapositive. Suppose $P \not \sqsubseteq _T Q$. Then there exist states p and q,  $tr' \in {\varSigma ^{\tau \surd }}^*$,  $b \in {\varSigma ^{\surd }}$ such that

Then by Lemma 20, there exist a trace $tr \in {\varSigma ^{\tau \surd }}^*$, states $\hat{p}$ and $\hat{q}$, and $\pi \in G$ such that

Further,

Taking $a = \pi (b)$ we have the result. $\square$

For example, in the reduced product automaton of Example 18, the refinement holds, and each visible transition of a state of Q is matched by a transition of the corresponding state of P.

Fig. 7

An explanation of counterexample unwinding: the path in the reduced product automaton is in the top row, and the path found in the standard product automaton is in the bottom row. Transitions are represented by solid arrows, and permutation bisimulations are represented by dashed arrows

The above proposition justifies the model checking algorithm in Fig. 6. The algorithm searches the reduced product automaton for a state $(\hat{p}, \hat{q})$ such that . We do not explicitly build the product automaton: instead we explore it on the fly, based on the specification and implementation of LTSs. The algorithm maintains a set seen of all states seen so far and a set pending of states that still need to be expanded; FDR implements pending as a queue, so as to perform a breadth-first search. Note that the algorithm is identical to the standard algorithm [14, 34], except for the application of rep to obtain the representative member. Hence, the highly optimised refinement algorithms of [14] can be used.

3.5 Counterexample generation

When FDR detects that a refinement assertion does not hold, it presents the user with an informative counterexample that explains why it does not hold. For example, if $P \sqsubseteq _T Q$ fails, then the counterexample is of the form $tr\frown \langle a\rangle$ where $tr \in traces(P) \cap traces(Q)$, but $tr\frown \langle a\rangle \in traces(Q)\setminus traces(P)$. FDR also allows the user to discover the contribution that each component makes to the counterexample.

Whenever FDR finds a new state, it records its predecessor state in the exploration. This allows FDR to construct the path followed through the reduced product automaton, i.e. a sequence of states $({\hat{p}}_0, \hat{q}_0), (\hat{p}_1, \hat{q}_1), \ldots (\hat{p}_n, \hat{q}_n)$. However, it does not record the labels of the transitions, nor the permutations used to produce representatives, in order to reduce memory usage. In order to produce the counterexample, it needs to find the corresponding path through the standard product automaton, together with the labels of transitions. The construction is illustrated in Fig. 7. Below we write $(p,q) \sim _\pi (p',q')$ for $\pi (p) = p' \wedge q \sim _\pi q'$.

The path in the standard product construction starts at the initial state $(p_0,q_0) = (init_P, init_Q)$. FDR can calculate the permutation $\pi _0$ such that $(p_0,q_0) \sim _{\pi _0} (\hat{p}_0, \hat{q}_0) = rep(p_0,q_0)$.

Suppose, inductively, we have a state $(p_i,q_i)$ of the standard product automaton and a permutation $\pi _i$ such that $(p_i,q_i) \sim _{\pi _i} (\hat{p}_i, \hat{q}_i)$. FDR needs to find b, $(p_{i+1}, q_{i+1})$ and $\pi _{i+1}$ such that $(p_{i}, q_{i}) \xrightarrow {b}_S (p_{i+1}, q_{i+1})$ and $(p_{i+1}, q_{i+1}) \sim _{\pi _{i+1}} (\hat{p}_{i+1}, \hat{q}_{i+1})$.

Consider the transition $(\hat{p}_i, \hat{q}_i) \xrightarrow { }_R (\hat{p}_{i+1}, \hat{q}_{i+1})$ in the reduced product automaton. FDR searches over the transitions of $(\hat{p}_i,\hat{q}_i)$ in the standard product automaton to find a transition $(\hat{p}_i,\hat{q}_i) \xrightarrow {a_i}_S (p_{i+1}',q_{i+1}')$ such that $rep(p_{i+1}',q_{i+1}') = (\hat{p}_{i+1}, \hat{q}_{i+1})$. Then $(\hat{p}_i,\hat{q}_i) \xrightarrow {a_i}_R (\hat{p}_{i+1},\hat{q}_{i+1})$ by construction of the reduced automaton. Also, since $(p_i,q_i) \sim _{\pi _i} (\hat{p}_i, \hat{q}_i)$, we have $(p_i,q_i) \xrightarrow {\pi _i^{-1}(a_i)}_S (p_{i+1}, q_{i+1})$ for some $(p_{i+1}, q_{i+1})$ such that $(p_{i+1}, q_{i+1})\sim _{\pi _i} (p_{i+1}', q_{i+1}')$. Let $\pi _i'$ be such that $(p_{i+1}',q_{i+1}') \sim _{\pi _i'} (\hat{p}_{i+1},\hat{q}_{i+1})$. (The permutation $\pi _i'$ is the one used by the representative function rep, so is easily found.) Then letting $\pi _{i+1} = \pi _i ; \pi _i'$, we have $(p_{i+1},q_{i+1}) \sim _{\pi _{i+1}} (\hat{p}_{i+1}, \hat{q}_{i+1})$, as required.

Continuing in this way, we can construct the path corresponding to the counterexample through the standard product automaton. This algorithm works efficiently in practice.

4 Symmetric datatypes

$\hbox {CSP}_M$ scripts are often defined using symbolic datatypes and are symmetric in subtypes of one or more such datatypes. The linked list-based example of the Introduction makes use of a datatype definition of the form

The resulting system is symmetric in the subtype excluding the special value Null.

We consider disjoint sets $T_1$,...,$T_N$, where each $T_i$ is a subset of a datatype ${{\hat{T}}}_i$ and contains only atomic values. We call the $T_i$distinguished subtypes and the ${{\hat{T}}}_i$distinguished supertypes. In the running example, the system is symmetric in the subtype NodeID of “real” node identities, but not in the containing supertype NodeIDType, which includes the special value Null. Likewise it is symmetric in the type Data and the type ThreadID. Let ${\mathcal {T}}= \bigcup _{i=1}^N T_i$. For the rest of this section, let $\pi \in Sym({\mathcal {T}})$ be a type-preserving permutation on ${\mathcal {T}}$, i.e. for each i,  $\pi$ maps values of type $T_i$ to $T_i$.

We assume a well-typed script. Below we will show that, subject to certain assumptions—mainly that the CSP script contains no constants from ${\mathcal {T}}$—the value of every expression is symmetric in those types.

We sketch the semantics of $\hbox {CSP}_M$. As described in Sect. 1.1, $\hbox {CSP}_M$ is a large language, with a powerful functional sub-language. We omit the full details here and refer the interested reader to [15]. We use an environment mapping identifiers (variables) to values:⁵. We write $\rho$, $\rho '$, etc., for environments. The type Expr represents expressions, including those that correspond to both processes and nonprocess values. The semantics of expressions is defined using a function such that $\mathsf{eval}\rho ~e$ gives the value of expression e in environment $\rho$. In particular, when $\mathsf{eval}$ is applied to an expression that represents a process, it will return the corresponding LTS, augmented as follows. For later convenience, we label each state with the corresponding syntactic expression—or control state—and environment. We define a label to be a pair $(P,\rho )$ where P is a syntactic expression⁶ and $\rho$ is an environment.

Definition 22

An augmented LTS is an LTS where each state is given a label, as above.

Thus $\mathsf{eval}\rho ~P$ will give an LTS whose root node has label $(P,\rho )$; equivalently, a node with label $(P,\rho )$ has semantics equal to $\mathsf{eval}\rho ~P$. For brevity, we will sometimes identify a state with its label.

Let $\pi$ be a type-preserving permutation on ${\mathcal {T}}$. We extend $\pi$ to other values in the obvious way; for example:

• For values x not depending on ${\mathcal {T}}$ we have $\pi (x) = x$.

• We lift $\pi$ to dotted values, including events, by $\pi (v_1.\ldots .v_n) = \pi (v_1).\ldots .\pi (v_n)$.

• We lift $\pi$ to tuples, sets, sequences, maps and values from datatypes by point-wise application.

• We lift $\pi$ to functions, considered as sets of maplets, by $\pi (f) = \{ \pi (x) \mapsto \pi (y) \mid x \mapsto y \in f \}$; equivalently, in terms of a lambda abstraction, $\pi (f) = \lambda z \cdot \pi (f(\pi ^{-1}(z)))$.

• We lift $\pi$ to labels by $\pi (P,\rho ) = (P,\pi \mathbin {\scriptstyle \circ }\rho )$.

• We lift $\pi$ to augmented LTSs by application of $\pi$ to the events of the transitions and to the labels of states.

  Note that if L is an augmented LTS, then $L \sim _\pi \pi (L)$.

Note that this lifting of $\pi$ forms a bijection on Value.

The following definition captures our main assumption about the CSP script.

Definition 23

A CSP script is constant-free for ${\mathcal {T}}$ if

• 1. The only constants from ${\mathcal {T}}$ that appear are within the definition of the distinguished types constituting ${\mathcal {T}}$ itself.

• 2. The script makes no use of the built-in functions seq, mapToList, mtransclose or show, or the compression functions deter, chase or chase_nocache [39].

Clearly, processes that use constants from ${\mathcal {T}}$ might not be symmetric: for example, $c!A \rightarrow STOP$, where $A \in {\mathcal {T}}$, is not symmetric in ${\mathcal {T}}$.

The built-in functions listed in item 2 can be used to introduce constants from ${\mathcal {T}}$ and so can break symmetry. For example, seq(s) converts the set s into a sequence (in an implementation-dependent way), so x = head(seq(T)) (where T is a distinguished subtype) effectively sets x to be a constant from T.

The compression functions in item 2 prune an LTS by removing transitions according to certain rules (but in an implementation-dependent way). Thus they can also break symmetry. For example, each of them could convert the LTS corresponding to into the LTS corresponding to $c!A \rightarrow STOP$, for an arbitrary $A \in T$.

The following is the main result of this section.

Proposition 24

Suppose a script is constant-free for ${\mathcal {T}}$, and let $\pi$ be a type-preserving permutation on ${\mathcal {T}}$.

• 1. The set of events is closed under $\pi$: $\pi ({\varSigma ^{\tau \surd }}) = {\varSigma ^{\tau \surd }}$. And likewise the set of values in each datatype is closed under $\pi$.

• 2. For every expression e in the script (which could correspond to a process or a nonprocess value), and every environment $\rho$,

  $$\begin{aligned} \pi (\mathsf{eval}\rho ~ e)= & {} \mathsf{eval}(\pi \mathbin {\scriptstyle \circ }\rho ) e . \end{aligned}$$

Proof

(sketch). The proof proceeds by a large structural induction over the syntax of $\hbox {CSP}_M$; it includes subsidiary results concerning other aspects of $\hbox {CSP}_M$, namely pattern matching, binding of variables, declarations and generators and qualifiers of set or sequence comprehensions. The proof is in [15]. $\square$

Corollary 25

Suppose a script is constant-free for ${\mathcal {T}}$, and let $\pi$ be a type-preserving permutation on ${\mathcal {T}}$. Let $\rho _1$ be the environment formed from the top-level declarations in the script. Then for every expression e in the script,

$$\begin{aligned} \pi (\mathsf{eval}\rho _1 ~ e)= & {} \mathsf{eval}\rho _1 e . \end{aligned}$$

Proof

This follows immediately from Proposition 24, since $\pi \mathbin {\scriptstyle \circ }\rho _1 = \rho _1$. $\square$

For example, this corollary shows that the LTSs representing the specification and implementation processes of each refinement check are $\pi$-symmetric.

The above results show that structural symmetry induces operational symmetry: when a system is constructed in a way that treats a family of processes symmetrically—as is required by the constant-free condition—then the induced LTS is symmetric in the identities of those processes. Further, when a system uses data with no distinguished values, then the induced LTS is symmetric in the type of that data.

We have extended FDR4 based on the above proposition. FDR can identify the largest subtype of a type for which the script is constant-free. Alternatively it can check that the script is indeed constant-free for a particular type, giving an informative error if not.

Related work. Previous approaches to symmetry reduction have been based on a much smaller language, with less support for complex datatypes, often performing symmetry reduction only on atomic values held in shared variables. Leuschel et al. [25] consider symmetry within the context of B, which includes deferred sets (similar to our distinguished types) together with tuples and sets; they prove a result similar to ours, in particular that the values of all invariants (predicates) are preserved by permutations of deferred types. Ip and Dill [19] and Bošnački et al. [3] also provide support for shared variables that store records and arrays; Ip and Dill give restrictions that ensure that elements of their symmetric types (called scalarsets) are treated symmetrically. Junttila provides support for lists, records, sets, multisets, associative arrays and union types. Each of these approaches is equivalent to a sub-language of the functional sub-language of $\hbox {CSP}_M$.

Donaldson and Miller [10] consider a language that allows processes to hold the identities of other processes, but not more complex datatypes.

To our knowledge, no other approach to symmetry reduction supports such a powerful and convenient language, supporting both a wide range of datatypes and the ability for processes to hold values based on symmetric types.

5 Symmetry reduction on supercombinators

The algorithm in Sect. 3 was at a fairly high level of abstraction. We now consider how to implement it within the context of FDR.

Internally, FDR uses a powerful and efficient implicit representation of an LTS, called a supercombinator [14]. It consists of some component LTSs, along with rules that describe how transitions of the components should be combined to give transitions of the whole system: FDR automatically determines which processes should be modelled as component LTSs, and automatically builds corresponding rules. This allows the process to be model checked on the fly, without explicitly constructing the whole state space. Supercombinators are generally applicable for modelling systems built from a number of components.

In the running example, FDR would create an LTS for each of the threads, each of the nodes, the lock and the top variable. FDR would then automatically build rules for the supercombinator that would combine the transitions of these LTSs, corresponding to the way the processes are combined using parallel composition and hiding. Strictly speaking, this is just one possible choice, since FDR uses various heuristics to optimise supercombinators, but it is the most natural choice. Each rule combines transitions of a subset of the components and determines the event the supercombinator performs.

In this section, in the interest of exposition, we give a slightly simplified version of supercombinators, which is adequate to deal with the vast majority of examples, in particular systems built from a number of sequential components, combined using a combination of parallel composition, hiding and renaming. In appendix, we generalise and give the full definition of supercombinators, which can represent arbitrary CSP combinations of processes.

Below, we formally define supercombinators and the induced LTS. We then prove a result that identifies circumstances under which two supercombinators induce $\pi$-bisimilar LTSs, where $\pi$ is an event permutation.

Let − be a value, not in ${\varSigma ^{\tau \surd }}$; we use it to denote a process performing no event. Let $\varSigma ^- = {\varSigma ^{\tau \surd }}\cup \{-\}$.

Definition 26

A simplified supercombinator is a pair $({\mathcal {L}}, {\mathcal {R}})$ where

• ${\mathcal {L}} = \langle L_1, \ldots , L_n\rangle$ is a sequence of component LTSs;

• ${\mathcal {R}}$ is a set of supercombinator rules (e, a) where

  $e \in (\varSigma ^-)^n$ specifies the action each component must perform, where − indicates that it performs none;

  and $a \in {\varSigma ^{\tau \surd }}$ is the event the supercombinator performs.

Given a supercombinator, a corresponding LTS can be constructed.

Definition 27

Let ${\mathcal {S}} = (\langle L_1, \ldots , L_n\rangle , {\mathcal {R}})$ be a supercombinator where $L_i = (S_i, \varDelta _i, init_i)$. The LTS induced by${\mathcal {S}}$ is the LTS $(S, \varDelta , init)$ such that:

• States are tuples consisting of the state of each component: $S \subseteq S_1 \times \cdots \times S_n$.

• The initial state is the tuple containing the initial states of each of the components:

  $$\begin{aligned} init= & {} (init_1, \ldots , init_n). \end{aligned}$$

• The transitions correspond to the supercombinator rules firing. Let

  $$\begin{aligned} \sigma = (s_1, \ldots , s_n), \qquad \sigma ' = (s'_1, \ldots , s'_n). \end{aligned}$$

  Then $(\sigma , a, \sigma ') \in \varDelta$ iff there exists $((b_1, \ldots , b_n),a) \in \mathcal {R}$ such that for each component i:

  if $b_i \ne -$ then $s_i \xrightarrow {b_i}_i s_i'$; and if $b_i = -$ then $s_i' = s_i$; i.e. component i performs $b_i$, or does nothing if $b_i = \mathord -$.

It is straightforward to define supercombinators corresponding to most CSP operators, including parallel composition, hiding and renaming, and to compose supercombinators hierarchically so as to define a single supercombinator for a system. The following example illustrates the ideas.

Example 28

Consider the system . Let $T = \{t_1,\ldots ,t_n\}$ and let the LTS for $P(t_i)$ be $L_i$, for each i. Then a possible supercombinator for this system would be

$$\begin{aligned} \begin{aligned}&(\;\langle L_1, \ldots , L_n\rangle ,\\&\quad \{(e_a, \hbox {if }a \in X \hbox {then }\tau \hbox {else }a) \mid a \in \textstyle \bigcup _{j=1}^n A(j) \} \cup \\&\qquad \{ (\delta _j, \tau ) \mid j \in \{1,\ldots ,n\}\} \;), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} e_a(i)= & {} \hbox {if }a \in A(t_i) \hbox {then }a \hbox {else }- \,, \\ \delta _j(i)= & {} \hbox {if }i=j \hbox {then }\tau \hbox {else }- \, . \end{aligned}$$

Each rule in the first set corresponds to a synchronisation on event a between all processes $P(t_i)$ such that $a \in A(t_i)$; that event a is then replaced by $\tau$ if $a \in X$. Each rule in the second set corresponds to the system performing $\tau$ as a result of $P(t_j)$ performing $\tau$.

5.1 Symmetries between supercombinators

We now consider symmetries between supercombinators, and how these correspond to symmetries between the corresponding LTSs. We are mainly interested in showing that the supercombinator corresponding to the implementation process in a refinement check is symmetric, i.e. $\pi$-bisimilar to itself for every event permutation $\pi$ in some group G. However, we want to do this without creating that complete LTS: instead we just perform checks on the components and rules. The following definition captures the relevant properties.

For the remainder of this section, fix an event permutation group $G \le EvSym$. Given a permutation $\pi \in G$, we extend it to $\varSigma ^-$ by defining $\pi (-) = \mathord {-}$.

Definition 29

Consider a supercombinator ${\mathcal {S}} = ({\mathcal {L}}, {\mathcal {R}})$ with $\mathcal {L} = \langle L_1, \ldots , L_n\rangle$. Let $\pi$ be an event permutation, and let $\alpha$ be a bijection from $\{1,\ldots ,n\}$ to itself; we call $\alpha$ a component bijection. We say that ${\mathcal {S}}$ is $\pi$-mappable to itself using $\alpha$ if:

• for every i,  $L_i \sim _\pi L_{\alpha (i)}$;

• if $(e,a) \in {\mathcal {R}}$ then there is a rule $(e',\pi (a)) \in {\mathcal {R}}$ such that $\forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i))$;

• if $(e',a) \in {\mathcal {R}}$ then there is a rule $(e,\pi ^{-1}(a)) \in {\mathcal {R}}$ such that $\forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i))$.

The first item shows how to map $L_i$ onto a $\pi$-bisimilar LTS $L_{\alpha (i)}$. The latter two items say that ${\mathcal {R}}$ acts on each LTS $L_i$ in the same way as it acts on $L_{\alpha (i)}$, but with the latter’s events renamed under $\pi$.

We sometimes write $\alpha$ as $\alpha _\pi$, to emphasise the event permutation $\pi$.

Example 30

Consider, again, the process

and its supercombinator from Example 28. Suppose, also, that the processes P(t) use data from some polymorphic type V, and that the script is constant-free for the types T and V.

Let $\pi$ be an event permutation formed by lifting permutations on T and V. For each $i \in \{1,\ldots ,n\}$, define $\alpha _{\pi }(i) = j$ such that $\pi (t_i) = t_j$; note that such a j exists, and that $\alpha _\pi$ is a bijection. Proposition 24 then tells us that

• the LTSs for $P(t_i)$ and $P(\pi (t_i))$ are $\pi$-bisimilar: $L_i \sim _\pi L_{\alpha (i)}$;

• $\pi (A(t_i)) = A(t_{\alpha (i)})$;

• $\pi (X) = X$.

The second and third items can be used to show that the rule set satisfies the conditions of Definition 29. For example, given the rule $(e_a, \hbox {if }a \in X \hbox {then }\tau \hbox {else }a)$, we can consider the rule $(e_{\pi (a)}, \hbox {if }\pi (a) \in X \hbox {then }\tau \hbox {else }\pi (a))$, and show that, for each i

$$\begin{aligned}&e_{\pi (a)}(\alpha (i)) = ( \hbox {if }~ \pi (a) \in A(t_{\alpha (i)}) \hbox {then }\pi (a) \hbox {else }-) \\&\quad = \pi (\hbox {if }~ a \in A(t_i) \hbox {then }e \hbox {else }-) \\&\quad = \pi (e_a(i)),\\&\pi (\hbox {if }~ a \in X \hbox {then }\tau \hbox {else }a)\\&\quad = (\hbox {if }~ \pi (a) \in X \hbox {then }\tau \hbox {else }\pi (a)), \end{aligned}$$

as required. Hence the supercombinator is $\pi$-mappable to itself using $\alpha$.

We now show that $\pi$-mappable supercombinators induce $\pi$-bisimilar LTSs.

Lemma 31

Let $\pi$ be an event permutation, and let $\mathcal {S} = (\langle L_1, \ldots , L_n\rangle , {\mathcal {R}})$ be $\pi$-mappable to itself using component bijection $\alpha$. Consider the relation $\approx _\pi$ defined over states of the induced LTSs by

$$\begin{aligned} \begin{aligned}&(s_1,\ldots ,s_n) \approx _\pi (s_1',\ldots ,s_n') \;\text{ iff }\\&\qquad \forall i \in \{1,\ldots ,n\} \cdot s_i \sim _{\pi } s'_{\alpha (i)}. \end{aligned} \end{aligned}$$

Then $\approx _\pi$ is a $\pi$-bisimulation. Further, the initial states of the two LTSs are related by $\approx _\pi$.

The proposition below follows easily from the above lemma.

Proposition 32

Suppose ${\mathcal {S}}$ is a supercombinator that is $\pi$-mappable to itself for every $\pi \in G$. Then the induced LTS is G-symmetric.

We now show that the property of supercombinators being mappable is compositional in the obvious way.

Lemma 33

Consider a supercombinator ${\mathcal {S}} = ({\mathcal {L}}, {\mathcal {R}})$. Suppose ${\mathcal {S}}$ is $\pi$-mappable to itself using $\alpha _\pi$ and is $\pi '$-mappable to itself using $\alpha _{\pi '}$. Then ${\mathcal {S}}$ is $(\pi ;\pi ')$-mappable to itself using $\alpha _{\pi } ; \alpha _{\pi '}$.

Proof

Suppose ${\mathcal {L}}= \langle L_1,\ldots ,L_n\rangle$. Consider $L_i$,  $L_{\alpha _\pi (i)}$ and $L_{\alpha _{\pi '}(\alpha _\pi (i))}$. Then $L_i \sim _\pi L_{\alpha _\pi (i)}$, and $L_{\alpha _\pi (i)} \sim _{\pi '} L_{\alpha _{\pi '}(\alpha _\pi (i))}$. Hence $L_i \sim _{\pi ; \pi '} L_{\alpha _{\pi '}(\alpha _\pi (i))}$.

Now consider the rules. Suppose $(e,a) \in {\mathcal {R}}$. Then there is a rule $(e',\pi (a)) \in {\mathcal {R}}$ such that $e'(\alpha _\pi (i)) = \pi (e(i))$ for each $i \in \{1,\ldots ,n\}$. But then there is a rule $(e'', (\pi ;\pi ')(a)) \in {\mathcal {R}}$ such that $e''(\alpha _{\pi '}(i)) = \pi '(e'(i))$ for each i. Hence, for each i,  $e''((\alpha _\pi ;\alpha _{\pi '})(i)) = e''(\alpha _{\pi '}(\alpha _{\pi }(i))) = \pi '(e'(\alpha _\pi (i))) = (\pi ;\pi ')(e(i))$. The reverse condition is very similar. $\square$

6 Identifying symmetries and applying permutations in supercombinators

In the last section we described sufficient conditions ($\pi$-mappability) for the LTS induced by a supercombinator to be $\pi$-symmetric. We now build on this for systems with symmetric datatypes. Let ${\mathcal {T}}$ be a collection of datatypes. Throughout this section we assume a constant-free script for ${\mathcal {T}}$. Let $\pi$ be an event permutation formed from lifting a type-preserving permutation on ${\mathcal {T}}$ to events; we write $EvSym({\mathcal {T}})$ for the set of all such event permutations. Let ${\mathcal {S}}_{impl}$ be the supercombinator for the implementation. In Sect. 6.1, we explain how we verify algorithmically that ${\mathcal {S}}_{impl}$ is $\pi$-mappable to itself, for every $\pi \in EvSym({\mathcal {T}})$, and describe pre-calculations that help in subsequent calculations of component bijections. We explain how to actually apply an event permutation to a state of a supercombinator in Sect. 6.2.

6.1 Checking mappability

In this section we explain how we verify that the supercombinator for the implementation process is $\pi$-mappable to itself for every $\pi \in EvSym({\mathcal {T}})$; by Proposition 32, this will mean that it is $EvSym({\mathcal {T}})$-symmetric. Assuming a constant-free script, FDR will nearly always produce such a supercombinator. (Recall that Corollary 25 talks about the LTS corresponding to the implementation process, rather than the supercombinator that represents that LTS.) However, it is not feasible to verify that FDR will always produce such a supercombinator: FDR uses various heuristics to decide how to construct supercombinators, which makes it too complex to reason about directly. We are also aware of a corner-case where this is not (currently) the case. We therefore verify mappability for each supercombinator generated. If this turns out not to be the case, our approach fails, and we give up (but we have never known this to happen on a noncontrived example).

We also describe some pre-calculations we make concerning component bijections, for use when exploring the product automaton. Note that we want to avoid pre-calculating and storing all such component bijections, since there are simply too many; instead, we calculate enough information for them to be calculated efficiently subsequently.

We attempt to prove that ${\mathcal {S}}_{impl}$ is $\pi$-mappable to itself, for every permutation $\pi$ of the distinguished types. However, by Lemma 33, it suffices to consider just permutations $\pi$ from a set of generators of the full symmetry group. So consider a supercombinator ${\mathcal {S}} = ({\mathcal {L}}, {\mathcal {R}})$, with ${\mathcal {L}}= \langle L_1,\ldots ,L_n\rangle$, and consider the problem of showing that ${\mathcal {S}}$ is $\pi$-mappable to itself. We split this into two parts, corresponding to the components and the rules.

Recall that each state of each component LTS has a label $(P, \rho )$, where P is a control state (a syntactic expression) and $\rho$ is an environment. Suppose each component $L_i$ has initial label $(P_i,\rho _i)$, so $L_i = \mathsf{eval}\rho _i~P_i$. Let

$$\begin{aligned} {\mathcal {P}}= \{(P_1,\rho _1),\ldots ,(P_n,\rho _n)\}. \end{aligned}$$

Our goal is to build a bijection $\alpha _\pi$ from $\{1,\ldots ,n\}$ to itself such that $P_{\alpha _\pi (i)} = P_i$ and $\rho _{\alpha _\pi (i)} = \pi \mathbin {\scriptstyle \circ }\rho _i$ for each i. We say that ${\mathcal {P}}$ is $\pi$-mappable to itself if this holds. Proposition 24 will then tell us that $L_{\alpha _\pi (i)} = \pi (L_i)$, so $L_i \sim _\pi L_{\alpha _\pi (i)}$, for each i.

Note, however, that the labels in ${\mathcal {P}}$ might not be distinct: we might be dealing with multisets rather than sets. In order to deal with such cases, we add a fresh dummy variable inst to each environment. Suppose there are k copies of a particular label $(P,\rho )$ in ${\mathcal {P}}$. We extend each of these environments by mapping inst to distinct integers in the range $\{1,\ldots ,k\}$, thereby distinguishing these labels. It is clear that if ${\mathcal {P}}$ is indeed $\pi$-mappable to itself then ${\mathcal {P}}$ will contain the same number k of copies of $(P,\rho )$ as of $(P,\pi \mathbin {\scriptstyle \circ }\rho )$; hence the extensions of $\rho$ and $\pi \mathbin {\scriptstyle \circ }\rho$ will use the same values $\{1,\ldots ,k\}$ for inst. We will define $\alpha _\pi$ to relate indices of environments that have the same value for inst.

We calculate a mapping $m_{{\mathcal {P}}}$ from labels in ${\mathcal {P}}$ to the corresponding index:

$$\begin{aligned} m_{{\mathcal {P}}}= & {} \{ (P_i, \rho _i) \mapsto i \mid i \in \{1,\ldots ,n\} \} . \end{aligned}$$

Note that $m_{{\mathcal {P}}}$ is indeed a mapping, because of the use of the inst variables. We then test whether ${\mathcal {P}}$ is indeed $\pi$-mappable to itself: for each $i \in \{1,\ldots ,n\}$, we calculate $(P_i,\pi \mathbin {\scriptstyle \circ }\rho _i)$ and check that it is in the domain of $m_{{\mathcal {P}}}$; if so, we define $\alpha _\pi (i)$ to be the index it maps to, so $P_{\alpha _\pi (i)} = P_i$ and $\rho _{\alpha _\pi (i)} = \pi \mathbin {\scriptstyle \circ }\rho _i$. If this check fails, then the supercombinator produced by FDR is not symmetric and our approach fails. If the check succeeds for every i, Proposition 24 tells us that $L_i \sim _{\pi } L_{\alpha _\pi (i)}$ for each i, as required.

Now consider the rules. We check that

• if $(e,a) \in {\mathcal {R}}$ then there is a rule $(e',\pi (a)) \in {\mathcal {R}}$ such that $\forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i))$;

• if $(e',a) \in {\mathcal {R}}$ then there is a rule $(e,\pi ^{-1}(a)) \in {\mathcal {R}}$ such that $\forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i))$.

If this succeeds, then ${\mathcal {S}}$ is $\pi$-mappable to itself.

Recall that we apply the above procedure to show that the supercombinator for the implementation, ${\mathcal {S}}_{impl}$, is $\pi _j$-mappable to itself, for every $\pi _j$ in a set of generators of the full symmetry group; we store each corresponding component bijection. Suppose event permutation $\pi$ can be written in terms of generators as $\pi = \pi _1;\ldots ;\pi _n$; then for each j,  ${\mathcal {S}}$ is $\pi _j$-mappable to itself using some component bijection $\alpha _{\pi _j}$, so ${\mathcal {S}}$ is $\pi$-mappable to itself using component bijection $\alpha _\pi = \alpha _{\pi _1} ; \ldots ; \alpha _{\pi _n}$, by Lemma 33.

6.2 Applying permutations to states

Suppose ${\mathcal {S}}$ is $\pi$-mappable to itself. We now explain how to apply permutation $\pi$ to a state of ${\mathcal {S}}$. The lemma below shows how, given components L and $L'$ such that $L' = \pi (L)$, to apply $\pi$ to a state of L to obtain a state of $L'$.

Lemma 34

Suppose L and $L'$ are components with $L' = \pi (L)$. Then for each state s of L, there is a state $s'$ of $L'$ such that $s \sim _\pi s'$. We write $\pi (s)$ for this state $s'$.

Proof

If s has label $(Q,\rho )$, then taking $s'$ to be the state with label $(Q,\pi \mathbin {\scriptstyle \circ }\rho )$ satisfies the conditions of the lemma. $\square$

We can apply the above lemma as follows. Internally to FDR, each component state is represented by an integer index, with the label of each state stored separately. For each component, we pre-calculate a mapping from labels to the corresponding state index. To find the state $s' = \pi (s)$ from Lemma 34, we obtain the label $(Q,\rho )$ of s, calculate the corresponding label $(Q,\pi \mathbin {\scriptstyle \circ }\rho )$ and find the index of the corresponding state using the above mapping.

The following proposition shows how, given a state $\sigma$ of a supercombinator and a permutation $\pi$, to calculate a state, which we denote $\pi (\sigma )$, such that $\sigma \sim _\pi \pi (\sigma )$.

Proposition 35

Let ${\mathcal {S}}$ be a supercombinator with components $\langle L_1,\ldots ,L_n\rangle$, and let $\pi$ be an event permutation. Suppose ${\mathcal {S}}$ is $\pi$-mappable to itself using component bijection $\alpha$. Consider the state $\sigma = ( s_1, \ldots , s_n).$ Define $\pi (\sigma )$ to be the state $(s_1', \ldots , s_n')$, where $s'_i = \pi (s_{\alpha ^{-1}(i)})$, constructed as described in Lemma 34. Then $\sigma \sim _\pi \pi (\sigma )$.

Proof

By construction, $s_i \sim _\pi s'_{\alpha (i)}$, for each i. Hence $\sigma \sim _\pi \pi (\sigma )$ by Lemma 31. $\square$

7 Calculating representatives

In this section, we describe an algorithm for calculating representatives (cf. Definition 16). Recall that we do not require unique representatives; however, we will aim for this to be the case in most examples, so as to give a better reduction in the state space.

Finding unique representatives is believed to be difficult in general. Clarke et al. [6] show that it is at least as hard as the graph isomorphism problem, which is widely accepted as being difficult (although not widely believed to be NP-complete).

Recall that a state of a supercombinator is a tuple $(s_1,\ldots ,s_n)$ where each $s_i$ is a state of a component LTS. However, we describe our algorithm in a slightly more general setting, to justify its more general applicability. We assume each state corresponds to a multiset $\{s_1,\ldots ,s_n\}$ of component states, and each component state contains a mapping from variables to values of distinguished types, together with (without loss of generality) a control state; for example, Promela fits into this setting. However, we use supercombinator states for examples.

We choose an ordering $\langle s_{i_1},\ldots ,s_{i_n}\rangle$ of the component states, so that, as far as possible, two $\pi$-bisimilar states map onto $\pi$-related orderings⁷; we describe the algorithm for ordering the components in Sect. 7.1. From this, we will, in Sect. 7.2, extract a particular ordering for each distinguished type and hence a representative. Again, this will be done so that, as far as possible, two $\pi$-bisimilar states map onto the same representative state.

Some steps of the algorithms below are left under-specified: the implementer may choose to implement them in one of several ways; however, in most such cases we require the step to be implemented in a symmetry-respecting way: if the step corresponds to application of a function f, then $f(\pi (x)) = \pi (f(x))$ for every element x of the domain of f, and each permutation $\pi$ lifted appropriately. In each case we suggest a particular symmetry-respecting implementation. However, there will be a couple of places where a symmetry-respecting implementation is not possible, and the algorithm will have to make an arbitrary decision (e.g. a random choice).

In Sect. 7.3 we study circumstances under which our algorithms do indeed give unique representatives, and show that this is often the case. In Sect. 7.4 we briefly discuss how our approach interacts with compression, and in Sect. 7.5 we discuss some implementation considerations and some variations on our approach. In Sect. 7.6 we compare our approach to others.

7.1 Component ordering algorithm

The component ordering algorithm takes a multiset $S = \{s_1, \ldots , s_n\}$ of component states, for example the component states of a supercombinator, and returns an ordering over S.

We will partition S by control states. We will likewise partition the states by the values of variables that do not depend on distinguished types.

For simplicity, we ignore, for the moment, nonsimple variables that hold tuples, sequences, sets, etc., that depend upon some distinguished supertype; we sketch how to deal with such variables below. Thus we consider just simple variables whose type is precisely that of some distinguished supertype; we call these distinguished variables. (Our impression is that using just the simple variables is normally adequate.) We assume some way of ordering the distinguished variables of a component state. We write $s(v_i)$ for the value of the ith distinguished variable in state s.

We build a multigraph model of each state: each node of the graph is a component state; there is an edge labelled (i, k) from $s_1$ to $s_2$ if $s_1(v_i) = s_2(v_k)$, where i and k range over indices of distinguished variables of $s_1$ and $s_2$ with the same type. In the running example, consider just Node processes, and order the variables in the order me, datum, next; then if $n_1$’s next field points to $n_2$ (i.e. equals $n_2$’s me field), there would be a (3, 1) edge from $n_1$ to $n_2$; this corresponds to how linked lists are typically depicted. Step 2 of the algorithm below is an adaptation of the naive refinement algorithm of [1, Section 6.4] to this multigraph model.

Definition 36

The component ordering algorithm takes a multiset of states S (e.g. the states of component LTSs of a supercombinator) and returns an ordering of S.

Fig. 8

Summary of the component ordering algorithm. The function split splits each element of a sequence of multisets, partitioning it according to an equivalence relation, and ordering the partition in a symmetry-respecting way. The equivalence relation $\approx$ tests whether two states have the same control states and values of variables of nondistinguished types. The equivalence relation $\equiv _n$ holds of $s_1$ and $s_2$ if $n(s_1) = n(s_2)$

The algorithm maintains a sequence of multisets of component states $\mathbf S = \langle S_1,\ldots , S_m\rangle$, such that $S_1,\ldots ,S_m$ partition S; we call this an ordered partition. For each j, all states in $S_j$ will have the same control state and hence the same number of variables of distinguished types. We refine the ordered partition in steps, until we obtain a sequence of singleton multisets. The algorithm is summarised in Fig. 8.

• 1. Start by partitioning states by their control states and the values of variables of nondistinguished types. Order these multisets in a symmetry-respecting way, e.g. lexicographically on control states and the values of nondistinguished variables, where a variable may take either a value of a distinguished subtype or a different value from the containing supertype, order the corresponding multisets in some symmetry-respecting way, e.g. those with distinguished values first.

• 2. Given an ordered partition $\mathbf S = \langle S_1, \ldots , S_m\rangle$, we split each $S_j$ based on matches between distinguished variables of each state s and distinguished variables of states in each element of the partition. Define $n_{i,j,k}(s)$ to be the number of (i, k) edges from s to elements of $S_j$:

  $$\begin{aligned} n_{i,j,k}(s)= & {} \# \{ s' \in S_j \mid s'(v_k) = s(v_i) \} , \end{aligned}$$

  where i ranges over indices of distinguished variables of s,  j ranges over $\{1,\ldots ,m\}$, and k ranges over indices of distinguished variables of $S_j$ with the same type as $v_i$.

  Then let n(s) be the tuple formed from the $n_{i,j,k}(s)$ (in lexicographic order of indices). If $n(s_1) = n(s_2)$ then the two states have the same relationship to states in other partitions.

  For each j, partition and order $S_j$ according to the states’ n-values. This produces a refined ordered partition.

  Repeat this step until no more progress is made.

• 3. If a multiset in the partition is not a singleton, then pick a nonsingleton multiset $S_j$, in some symmetry-respecting way; for example, pick the first nonsingleton multiset. Then split $S_j$ into two or more multisets, ordered in some way; for example, pick an arbitrary element $s \in S_j$, and split $S_j$ into ${\langle \{s\}, S_j \setminus \{s\} \rangle }$. Then return to step 2.

  Otherwise all multisets are singletons, so return the corresponding sequence of states.

Example 37

We apply the above algorithm to the node processes of the running example, using the suggested approaches.

We introduce suggestive notation: we write $N(m, d, n)$ for the state $(node, \{\textsf {me} \mapsto m, \textsf {datum} \mapsto d, {\textsf {next} \mapsto n}\})$, where node is the control state corresponding to the right-hand side of the definition of Node; we write $FN(m)$ for a FreeNode process, similarly.

Consider the multiset of processes

$$\begin{aligned}&\{N({\textsf {N}_{\textsf {0}}}, \textsf {B}, {\textsf {N}_{\textsf {4}}}), \, N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}}), \, FN({\textsf {N}_{\textsf {2}}}), \\&\quad N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {1}}}), \, N({\textsf {N}_{\textsf {4}}}, \textsf {B}, \textsf {Null}), \, FN({\textsf {N}_{\textsf {5}}})\}. \end{aligned}$$

This represents a linked list of four nodes (${\textsf {N}_{\textsf {3}}}$, ${\textsf {N}_{\textsf {1}}}$, ${\textsf {N}_{\textsf {0}}}$, ${\textsf {N}_{\textsf {4}}}$), all containing B, together with two free nodes (${\textsf {N}_{\textsf {2}}}$, ${\textsf {N}_{\textsf {5}}}$).

Step 1 then partitions the processes as follows, assuming the control state for $FN$ is less than that for $N$:

$$\begin{aligned}&\langle \{FN({\textsf {N}_{\textsf {2}}}), FN({\textsf {N}_{\textsf {5}}})\} , \\&\quad \{N({\textsf {N}_{\textsf {0}}}, \textsf {B}, {\textsf {N}_{\textsf {4}}}), N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}}), N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {1}}})\} ,\\&\quad \{N({\textsf {N}_{\textsf {4}}}, \textsf {B}, \textsf {Null})\}\rangle . \end{aligned}$$

For step 2, the n-value for $N({\textsf {N}_{\textsf {0}}}, \textsf {B}, {\textsf {N}_{\textsf {4}}})$ is $\langle 0 , 1, 1, 0; 3, 1; 0, 0, 1, 1 \rangle$ (semicolons used to improve readability). The first four entries correspond to the value ${\textsf {N}_{\textsf {0}}}$, counting the number of matches against variables in the first multiset, the me and next variables in the second multiset and the me variables in the third multiset, respectively; the next two entries correspond to the value B; the last four entries correspond to ${\textsf {N}_{\textsf {4}}}$. The n-values for $N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}})$ and $N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {1}}})$ are $\langle 0, 1, 1, 0; 3, 1; 0, 1, 1, 0 \rangle$ and $\langle 0, 1, 0, 0; 3, 1; 0, 1, 1, 0 \rangle$, respectively. However, the n-values for the two $FN$ processes are each $\langle 1,0,0,0\rangle$. Partitioning according to these n-values gives the following ordered partition:

$$\begin{aligned}&\langle \{FN({\textsf {N}_{\textsf {2}}}), FN({\textsf {N}_{\textsf {5}}})\} , \{N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {1}}})\}, \{N({\textsf {N}_{\textsf {0}}}, \textsf {B}, {\textsf {N}_{\textsf {4}}})\}, \\&\quad \{N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}})\}, \{N({\textsf {N}_{\textsf {4}}}, \textsf {B}, \textsf {Null})\}\rangle . \end{aligned}$$

Repeating step 2 makes no further progress. (Note that if we had started with a longer linked list, we would have needed more iterations of step 2: step 1 splits off the final node; the first iteration of step 2 splits off the first and penultimate nodes; the second iteration splits off the second and antepenultimate nodes; and so on.)

Finally, step 3 splits the nonsingleton multiset arbitrarily, say producing

$$\begin{aligned} \begin{aligned}&\langle \{FN({\textsf {N}_{\textsf {2}}})\}, \{FN({\textsf {N}_{\textsf {5}}})\} , \{N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {1}}})\}, \{N({\textsf {N}_{\textsf {0}}}, \textsf {B}, {\textsf {N}_{\textsf {4}}})\}, \\&\quad \{N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}})\}, \{N({\textsf {N}_{\textsf {4}}}, \textsf {B}, \textsf {Null})\} \rangle . \end{aligned} \end{aligned}$$

All multisets are now singleton, so the process is complete.

Note that if we had started with any other system representing a linked list of four nodes, all containing the same value, we would have ended up with an equivalent ordering, starting with the free nodes, ordered arbitrarily, followed by the first, third, second and fourth nodes of the list, in that order.

Recall that we assumed that all variables hold simple values of distinguished types. We sketch how the technique could be extended to more complex types. A tuple of n values could be considered instead as n distinct variables. For a variable holding a sequence, the length l could be considered as part of the control state, and then the elements could be considered as l distinct variables. It is less straightforward to fully deal with variables that hold sets, but it is possible to adapt the definition of n-values, for example by testing whether the value of one variable is an element of another (set-valued) variable. We have not implemented these techniques, but instead simply ignore variables holding complex values (in the representative choosing algorithm: the algorithms of earlier sections do fully support them): our experience is that our implementation is adequate, and we have not come across an example where using complex variables would help.

7.2 Permutation generation

We now describe how to go from an ordering on component states to an ordering of each distinguished type.

Definition 38

Let T be a distinguished subtype. The type ordering algorithm for T takes an ordering of component states and returns an ordering of T, as follows: it lists the values of type T in the order they appear in the ordering of component states, removes duplicates, and (if necessary) appends remaining values of T in an arbitrary order.

Example 39

Recall that in Example 37 we obtained the ordering of states

$$\begin{aligned} \begin{aligned}&\langle FN({\textsf {N}_{\textsf {2}}}), FN({\textsf {N}_{\textsf {5}}}) , N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {1}}}), N({\textsf {N}_{\textsf {0}}}, \textsf {B}, {\textsf {N}_{\textsf {4}}}), \\&\quad N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}}), N({\textsf {N}_{\textsf {4}}}, \textsf {B}, \textsf {Null}) \rangle . \end{aligned} \end{aligned}$$

Applying the type ordering algorithm can give

$$\begin{aligned} \langle {\textsf {N}_{\textsf {2}}}, {\textsf {N}_{\textsf {5}}}, {\textsf {N}_{\textsf {3}}}, {\textsf {N}_{\textsf {1}}}, {\textsf {N}_{\textsf {0}}}, {\textsf {N}_{\textsf {4}}}\rangle \quad \text{ and }\quad \langle \textsf {B}, \textsf {A}, \textsf {C}, \textsf {D} \rangle , \end{aligned}$$

where in the latter case the ordering of all except $\textsf {B}$ is arbitrary. (This particular example contains a large amount of arbitrariness because the initial state contains so few values from Data.)

The following algorithms produce a corresponding permutation $\pi$ on the distinguished subtypes and hence a representative.

Definition 40

The permutation generating algorithm proceeds as follows, given an ordering $\mathbf s$ of the component states. For each distinguished subtype $T = \{A_1, \ldots , A_N\}$, run the type ordering algorithm for T to obtain an ordering $\langle A_{i_1}, \ldots , A_{i_N}\rangle$ of T; then define the permutation function $\pi _T = \{{A_{i_1} \mapsto A_1,} \ldots , A_{i_N} \mapsto A_N\}$. Let $\pi$ be the union of the individual $\pi _T$.

The representative generating algorithm, given a set S of component states, runs the component ordering algorithm on S to obtain a component ordering $\mathbf s$, then runs the permutation generating algorithm on $\mathbf s$ to obtain a permutation $\pi$ and then returns $\pi (S)$. (In the case of S being the states of a supercombinator, $\pi (S)$ is calculated as in Proposition 35.)

Figure 9 summarises these algorithms.

Fig. 9

The permutation and representative generating algorithms

Example 41

Based on the orderings from Example 39, we obtain the permutation functions

$$\begin{aligned} \pi _{NodeID}= & {} \{{\textsf {N}_{\textsf {2}}} \mapsto {\textsf {N}_{\textsf {0}}}, {\textsf {N}_{\textsf {5}}} \mapsto {\textsf {N}_{\textsf {1}}}, {\textsf {N}_{\textsf {3}}} \mapsto {\textsf {N}_{\textsf {2}}}, \\&{\textsf {N}_{\textsf {0}}} \mapsto {\textsf {N}_{\textsf {3}}}, {\textsf {N}_{\textsf {1}}} \mapsto {\textsf {N}_{\textsf {4}}}, {\textsf {N}_{\textsf {4}}} \mapsto {\textsf {N}_{\textsf {5}}}\},\\ \pi _{Data}= & {} \{ \textsf {B}\mapsto \textsf {A}, \textsf {A} \mapsto \textsf {B}, \textsf {C} \mapsto \textsf {C}, \textsf {D} \mapsto \textsf {D} \}. \end{aligned}$$

Let $\pi = \pi _{NodeID} \cup \pi _{Data}$. Applying $\pi$ to the original vector of processes from Example 37, as in Proposition 35, we obtain the vector of processes

$$\begin{aligned} \begin{aligned}&\langle FN({\textsf {N}_{\textsf {0}}}), FN({\textsf {N}_{\textsf {1}}}), N({\textsf {N}_{\textsf {2}}}, \textsf {A}, {\textsf {N}_{\textsf {4}}}), N({\textsf {N}_{\textsf {3}}}, \textsf {A}, {\textsf {N}_{\textsf {5}}}), \\&\quad N({\textsf {N}_{\textsf {4}}}, \textsf {A}, {\textsf {N}_{\textsf {3}}}), N({\textsf {N}_{\textsf {5}}}, \textsf {A}, \textsf {Null}) \rangle . \end{aligned} \end{aligned}$$

In the generation of $\pi$, we made two arbitrary decisions. First, in step 3 of Example 37, we chose an arbitrary order for the two $FN$s. Second, in Example 39, we chose an arbitrary order for all elements of Data except $\textsf {B}$. However, note that if we had made these decisions in any other way, we would have obtained the same final vector of processes, essentially because the initial vector is symmetric in $\{{\textsf {N}_{\textsf {2}}}, {\textsf {N}_{\textsf {5}}}\}$ and in $\{\textsf {A},\textsf {C},\textsf {D}\}$.

Note, further, that if we had started with any vector of processes that was symmetric to the chosen initial vector—that is, representing a linked list of four nodes, all containing the same datum—then we would have ended up with the same final vector of processes. That is, the above vector is a unique representative for its equivalence class.

The following lemma relates permutations obtained from related vectors of processes.

Lemma 42

If the permutation generating algorithm applied to $\mathbf s$ gives $\pi _1$, then the permutation generation algorithm applied to $\pi (\mathbf s )$ gives a function that agrees with $\pi _1 \mathbin {\scriptstyle \circ }\pi ^{-1}$ on all distinguished values that appear in $\pi (\mathbf s )$.

Proof

Suppose the T-ordering algorithm applied to $\mathbf s$ produces $\langle A_{i_1}, \ldots , A_{i_N}\rangle$, where $A_{i_1},\ldots ,A_{i_k}$ appear in $\mathbf s$, and the other values are ordered arbitrarily. Then $\pi (A_{i_1}),\ldots ,\pi (A_{i_k})$ appear in the corresponding order in $\pi (\mathbf s )$, so the T-ordering algorithm applied to $\pi (\mathbf s )$ produces $\langle \pi (A_{i_1}),\ldots ,\pi (A_{i_k})\rangle$ followed by an arbitrary ordering of $\pi (A_{i_{k+1}}),\ldots ,\pi (A_{i_N})$.

Then the permutation generating algorithm applied to $\mathbf s$ gives

$$\begin{aligned} \pi _1= & {} \{{A_{i_1} \mapsto A_1}, \ldots , A_{i_N} \mapsto A_N\}. \end{aligned}$$

And the permutation generating algorithm applied to $\pi (\mathbf s )$ gives a function that includes $\{\pi \}(A_{i_1}) \mapsto A_1, \ldots , \pi (A_{i_k}) \mapsto A_k$, and maps $\pi (A_{i_{k+1}}), \ldots , \pi (A_{i_N})$ to an arbitrary permutation of $A_{k+1}, \ldots ,A_N$. But the above partial function equals

$$\begin{aligned} \{\pi (A_{i_1}) \mapsto \pi _1(A_{i_1}), \ldots , \pi (A_{i_k}) \mapsto \pi _1(A_{i_k})\}, \end{aligned}$$

which agrees with $\pi _1 \mathbin {\scriptstyle \circ }\pi ^{-1}$ on the distinguished values $\pi (A_{i_1}),\ldots ,\pi (A_{i_k})$ that appear in $\pi (\mathbf s )$. $\square$

7.3 Uniqueness of representations

We now consider circumstances under which the above algorithms, with the suggested implementations, give unique representatives. The following example shows that this is not always the case.

Example 43

Consider the set of processes

$$\begin{aligned} \begin{aligned}&\{\;N({\textsf {N}_{\textsf {0}}}, \textsf {A}, {\textsf {N}_{\textsf {1}}}),\; N({\textsf {N}_{\textsf {1}}}, \textsf {A}, {\textsf {N}_{\textsf {2}}}),\\&\quad N({\textsf {N}_{\textsf {2}}}, \textsf {B}, {\textsf {N}_{\textsf {3}}}),\; N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}}) \; \}. \end{aligned} \end{aligned}$$

For simplicity, suppose $\textsf {NodeID} = \{{\textsf {N}_{\textsf {0}}},{\textsf {N}_{\textsf {1}}},{\textsf {N}_{\textsf {2}}}, {\textsf {N}_{\textsf {3}}}\}$ and $\textsf {Data} = \{\textsf {A},\textsf {B}\}$. The above vector represents a circular linked list; such a state could not arise in our running example, but could in different linked list algorithms.

Applying steps 1 and 2 of the component ordering algorithm fails to split the processes. It is straightforward to check that, depending upon whether step 3 chooses to split off a node with the same or a different datum from the following node, the algorithm could produce either of the following vectors of processes:

$$\begin{aligned} \begin{aligned}&\langle N({\textsf {N}_{\textsf {0}}}, \textsf {A}, {\textsf {N}_{\textsf {3}}}), N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {2}}}), N({\textsf {N}_{\textsf {2}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}}), N({\textsf {N}_{\textsf {3}}}, \textsf {A}, {\textsf {N}_{\textsf {1}}}) \rangle , \\&\langle N({\textsf {N}_{\textsf {0}}}, \textsf {A}, {\textsf {N}_{\textsf {3}}}), N({\textsf {N}_{\textsf {1}}}, \textsf {B}, {\textsf {N}_{\textsf {2}}}), N({\textsf {N}_{\textsf {2}}}, \textsf {A}, {\textsf {N}_{\textsf {0}}}), N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {1}}}) \rangle . \end{aligned} \end{aligned}$$

Similarly, any other cycle of four nodes holding two different values arranged in adjacent pairs will produce one of these two final vectors. However, the choice of how to split at step 3 might be made differently on different such cycles. Thus our approach might not give unique representatives in this case. However, it does give a good reduction, from 24 cases to 2. Note, also, that the approach does give unique representatives for rings that contain different numbers of $\textsf {A}$s and $\textsf {B}$s, or where the data are in an alternating sequence such at $\langle \textsf {A},\textsf {B},\textsf {A},\textsf {B}\rangle$ round the ring.

Note that the above example is somewhat unrealistic. In a more realistic setting, there would be an external pointer into the ring (comparable to Top in the running example), which would be enough to break the symmetry, and so avoid having to make arbitrary decisions.

The permutation generating algorithm is potentially nondeterministic, because of the arbitrary choices in step 3 of the component ordering algorithm and in the type ordering algorithm. The latter nondeterminism is clearly irrelevant, since it only affects the result of the final permutation on values that do not appear, and so does not affect the final state obtained. (Note that, while we would expect any implementation to be deterministic, we are interested here in nondeterminism of the specification.) In fact, the nondeterminism may lead to a representative not being its own representative.

We show that in the case that the arbitrary choices in the component ordering algorithm do not cause nondeterminism of the outcome—i.e. for each input state, the final state is independent of how those choices are made—the algorithm produces unique representatives.

Lemma 44

Suppose that the representative generating algorithm when run on input states S always produces final states $S'$. Then if the algorithm is run on input state $\pi (S)$, it again always produces final state $S'$.

Proof

Consider first the component ordering algorithm. It is easy to see that this algorithm treats $\pi (S)$ and S equivalently. More precisely, if the algorithm is run in parallel on these two states, for each intermediate ordered partition $\langle \pi (S_1),\ldots ,\pi (S_m)\rangle$ obtained from $\pi (S)$, it is also possible for $\langle S_1,\ldots ,S_m\rangle$ to be obtained from S. Hence if the component ordering algorithm applied to $\pi (S)$ can produce the ordering $\pi (\mathbf s )$, then when applied to S it can produce $\mathbf s$.

Now suppose the permutation generating function applied to $\mathbf s$ produces $\pi _1$. Then by Lemma 42, the permutation generating function applied to $\pi (\mathbf s )$ gives a function that agrees with $\pi _1 \mathbin {\scriptstyle \circ }\pi ^{-1}$ on all distinguished values that appear in $\pi (S)$. Applying these permutations to the initial states, we obtain $\pi _1(S)$ in each case. By assumption, this value must equal $S'$, as required. $\square$

Corollary 45

Suppose the representative generating algorithm is deterministic on all inputs. Then it returns unique representatives.

We now investigate conditions under which the representative generating algorithm is deterministic. Our discussion from this point on is more specific to our supercombinator setting than the prior parts of this section, because we need to talk about mappings between components of the supercombinator. However, we believe that our results will carry over to other settings. We need a couple of additional definitions and technical lemmas.

Recall that in Sect. 6 we defined, for each $\pi \in EvSym({\mathcal {T}})$, a mapping $\alpha _\pi$ between the components of the supercombinator. We define a nonempty set of components to be a symmetric set if it is closed under all such $\alpha _\pi$ and minimal; i.e. each component maps, under some $\alpha _\pi$, to each other in the same symmetric set. In the running example, there would be four symmetric sets corresponding to the Node processes, the Thread processes, Top and Lock. We assume, without loss of generality, that processes in different symmetric sets have different control states, so the first step of the component ordering algorithm has the effect of partitioning based on symmetric sets.

Certain variables act as identities for processes. For example, the me variables act as identity variables for the node processes. These variables take the same value throughout the process’s execution. We will show (Proposition 50) that if the supercombinator uses unique identities (Definition 46), and at step 3 of the component ordering algorithm, we split only sets that are fully symmetric (Definition 49), then we obtain unique representatives.

Definition 46

We say that a supercombinator has unique identities if, for each nonsingleton symmetric set, all processes have an identity variable, and no two processes in the same symmetric set have the same value for that identity variable.

Our running example satisfies this condition: the two nonsingleton symmetric sets correspond to the Node and Thread processes; these have identities of types NodeID and ThreadID, with distinct identities for different processes.

Lemma 47

Suppose a supercombinator has unique identities. Consider a state $(s_1,\ldots ,s_n)$ of the supercombinator, and suppose $s_i$ and $s_j$ are in the same symmetric set, and $s_j = \pi (s_i)$. Then $j = \alpha _\pi (i)$.

Proof

If the symmetric set is a singleton, the result is trivial. Otherwise, let $id_i$ and $id_j$ be the values of the identity variable in $s_i$ and $s_j$, respectively, so $id_j = \pi (id_i)$. Then the identities in the initial states of these components are the same and so are similarly related. Note that component $\alpha _\pi (i)$ has identity $\pi (id_i)$, by definition of $\alpha _\pi$. No other component has that identity, by assumption. Hence $j = \alpha _\pi (i)$. $\square$

Lemma 48

Suppose a supercombinator has unique identities. Consider states $\sigma = (s_1,\ldots ,s_n)$, and $\sigma ' = (s_1',\ldots , s_n',)$, and suppose that for each symmetric set $\{i_1,\ldots ,i_k\}$ we have $\{\pi (s_{i_1}),\ldots , \pi (s_{i_k})\} = \{s_{i_1}',\ldots ,s_{i_k}'\}$ (i.e. the symmetric set maps onto itself under $\pi$). Then $\sigma ' = \pi (\sigma )$.

Proof

Suppose $\pi (s_{i_i}) = s'_{i_j}$ with $i_i$ and $i_j$ in the same symmetric set. Then by Lemma 47, $i_j = \alpha _\pi (i_i)$. So $s'_{\alpha _\pi (i)} = \pi (s_i)$, for each i. The result then follows from Proposition 35. $\square$

The following definition and proposition identify a condition under which splitting a set at step 3 of the component ordering algorithm does not introduce nondeterminism.

Definition 49

Given an ordered partition $\langle S_1,\ldots , S_m\rangle$, we say that the component $S_j$ is fully symmetric if for all $s, s' \in S_j$, there exists a permutation $\pi _1$ such that $\pi _1(s) = s'$, and $\pi _1(S_i) = S_i$ for each i.

In Example 37, the set $\{FN({\textsf {N}_{\textsf {2}}}), FN({\textsf {N}_{\textsf {5}}})\}$ split by step 3 is fully symmetric. However, in Example 43, the set $\{ N({\textsf {N}_{\textsf {0}}}, \textsf {A}, {\textsf {N}_{\textsf {1}}}), N({\textsf {N}_{\textsf {1}}}, \textsf {A}, {\textsf {N}_{\textsf {2}}}), N({\textsf {N}_{\textsf {2}}}, \textsf {B}, {\textsf {N}_{\textsf {3}}}), N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}})\}$ split by step 3 is not symmetric: for example, if $\pi _1$ is such that $\pi _1(N({\textsf {N}_{\textsf {0}}}, \textsf {A}, {\textsf {N}_{\textsf {1}}})) = N({\textsf {N}_{\textsf {1}}}, \textsf {A}, {\textsf {N}_{\textsf {2}}})$, then $\pi _1(N({\textsf {N}_{\textsf {3}}}, \textsf {B}, {\textsf {N}_{\textsf {0}}}))$ is of the form $N(n, \textsf {B}, {\textsf {N}_{\textsf {1}}})$, for some n, which is not a member of the set.

Proposition 50

Suppose that a supercombinator has unique identities. Suppose further that whenever we apply step 3 of the component ordering algorithm to split a set $S_j$, that set is fully symmetric. Then if we apply the above representative generating algorithm to a set S of states of the supercombinator, the result is independent of the precise value split off by step 3; i.e. the algorithm is deterministic. Hence the algorithm returns unique representatives.

Proof

Consider the effect of running the component ordering algorithm, starting from $S = \{s_1,\ldots ,s_n\}$. Consider two ordered partitions $\langle S_1,\ldots ,S_m\rangle$ and $\langle S_1',\ldots , S_m'\rangle$ that could be reached after the same number of steps, maybe corresponding to splitting off different elements at step 3. (It is clear that these partitions have the same number of elements.) We show by induction that there is some permutation $\pi$ such that $S_i' = \pi (S_i)$ for each i. It is clear that this is established by step 1 of the algorithm (with $\pi$ the identity permutation) and maintained by each iteration of step 2 (since the n-values will agree). Consider instances of step 3, splitting off s from $S_j$ and $\pi (s')$ from $\pi (S_j)$ where $s' \in S_j$; these produce

$$\begin{aligned} \langle S_1, \ldots , S_{j-1}, \{s\}, S_j-\{s\}, S_{j+1}, \ldots , S_m\rangle \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\langle \pi (S_1), \ldots , \pi (S_{j-1}), \{\pi (s')\}, \pi (S_j)-\{\pi (s')\}, \\&\qquad \pi (S_{j+1}), \ldots , \pi (S_m)\rangle . \end{aligned} \end{aligned}$$

Let $\pi _1$ be as in Definition 49, so $\pi _1(s) = s'$ and $\pi _1(S_i) = S_i$ for each i. Let $\pi ' = \pi \mathbin {\scriptstyle \circ }\pi _1$. It is then straightforward to check that the resulting ordered partitions are related by $\pi '$.

Hence any two final sequences of states produced by the component ordering algorithm will be of the form

$$\begin{aligned} \mathbf s = \langle s_1',\ldots ,s_n'\rangle \quad \text{ and }\quad \pi (\mathbf s ) = \langle \pi (s_1'),\ldots ,\pi (s_n')\rangle \end{aligned}$$

for some permutation $\pi$. But each pair of corresponding states $s_i'$ and $\pi (s_i')$ is from the same symmetric set (since step 1 of the component ordering algorithm partitions by symmetric sets). Thus, for each symmetric set $\{i_1,\ldots ,i_k\}$, we have $\{\pi (s_{i_1}),\ldots , \pi (s_{i_k})\} = \{s_{i_1},\ldots ,s_{i_k}\}$. Hence, by Lemma 48 (with $\sigma ' = \sigma$), $\pi (\sigma ) = \sigma$.

Now, if the permutation generating function applied to the component ordering $\mathbf s$ gives $\pi _1$, then the permutation generating function applied to $\pi (\mathbf s )$ gives $\pi _1\mathbin {\scriptstyle \circ }\pi ^{-1}$, by Lemma 42. Hence applying the two resulting permutations to the initial states S we obtain $\pi _1(S)$ and $(\pi _1\mathbin {\scriptstyle \circ }\pi ^{-1})(S) = (\pi _1\mathbin {\scriptstyle \circ }\pi ^{-1})(\pi (S)) = \pi _1(S)$, i.e. the same value in each case, as required.

Hence the algorithm produces unique representatives, by Corollary 45. $\square$

We show that the above proposition can be applied in fairly common circumstances.

Corollary 51

Consider a system representing a reference-linked data structure, using Node processes parametrised as in the running example (and no other processes), i.e. every node is of the form Node(me,datum,next) or FreeNode(me) where me is an identity variable. Suppose further than in every state, the nodes are arranged in a single linked list, possibly with some free nodes: in other words, each node has at most one predecessor, so the next references form a single list, rather than a tree or forest. Then the algorithm produces unique representatives.

Proof

As in Example 37, each iteration of step 2 of the component ordering algorithm strips off two more nodes from the list. This continues until the only nonsingleton set (if any) contains the free nodes. The system is then fully symmetric. (Since the identities of the free nodes appear nowhere else, and the free nodes contain no data, in fact, the result still holds if the free nodes hold a single piece of data.) The result then follows from Proposition 50. $\square$

The premise of Corollary 51—that there are no processes other than the node processes—is unrealistic. However, in most circumstances the result is still applicable. Suppose, in addition, we have some processes that represent threads operating on the linked list. For simplicity, suppose that step 3 of the component ordering algorithm is used to split sets of nodes before it is used to split sets of thread processes. In most cases, each thread process will have a reference to at least one node, which will then allow such sets to be split by an application of step 2. A common exception will be when several threads are in their initial state, but in this case the set of such threads will be fully symmetric, and so Proposition 50 can be applied to deduce that unique representatives are obtained. A somewhat contrived example where unique representatives are not obtained is with the set of processes

$$\begin{aligned} \begin{aligned} \{&Thread'({\textsf {T}_{\textsf {1}}}, \textsf {A}, \textsf {A}), Thread'({\textsf {T}_{\textsf {2}}}, \textsf {A}, \textsf {B}), \\&\quad Thread'({\textsf {T}_{\textsf {3}}}, \textsf {B}, \textsf {A}), Thread'({\textsf {T}_{\textsf {4}}}, \textsf {B}, \textsf {B})\}, \end{aligned} \end{aligned}$$

for some state $Thread'$, and where $\textsf {A}$ and $\textsf {B}$ are data values that are not stored in any node: in this case, different representatives are obtained depending on whether step 3 splits off a process holding two copies of the same data value or two distinct values.

The following example justifies the requirement that the nodes form a single list.

Example 52

Consider a reference-linked collection of seven nodes, arranged as on the left, below.

Steps 1 and 2 of the component ordering algorithm will split the nodes into three sets, corresponding to the three columns in the picture. If the set corresponding to the first column is split, then different representatives will be obtained, depending on whether the node split off has the same datum as its successor, or not.

Now consider the arrangement of six nodes on the right. This similarly does not give unique representatives.

The final lemma applies in most realistic examples and includes examples using trees.

Lemma 53

Consider a system representing a reference-linked data structure, where we now allow a node to have several references (held in distinct variables). Suppose that in addition there are some other distinguished (nonindexed) processes that may hold a reference to a node (like the Top process in the running example). Suppose that every nonfree node can be reached from one of these distinguished variables by following references. Then the algorithm produces unique representatives.

Proof

Consider running the component ordering algorithm. The nodes referenced by the distinguished variables will be stripped off by the first iteration of step 2 (and placed into singleton sets). The remaining nonfree nodes can inductively be stripped off by subsequent iterations, since all are reachable. The free nodes can be dealt with as in Corollary 51. $\square$

7.4 On compression

As mentioned earlier, FDR uses various compressions. For example, it will automatically compress each leaf LTS, factoring it by strong bisimulation. Compression and symmetry reduction work well together: their combination produces smaller state spaces than either technique on its own. However, they do not combine perfectly, as we now explain.

Suppose an uncompressed LTS L contains two strongly bisimilar states $s_1 = (Q_1,\rho _1)$ and $s_2 = (Q_2,\rho _2)$. Then FDR will pick one of them, say $s_1$, as the representative of its bisimilarity equivalence class, to include in the compressed LTS. Now consider the uncompressed LTS $L' = \pi (L)$. This has strongly bisimilar states $s_1' = (Q_1,\pi \mathbin {\scriptstyle \circ }\rho _1)$ and $s_2' = (Q_2,\pi \mathbin {\scriptstyle \circ }\rho _2)$. If FDR picks $s_1'$ as the representative of its bisimilarity equivalence class, the compression and symmetry reduction combine well: given two $\pi$-bisimilar states $\sigma$ and $\sigma '$ that contain $s_1$ and $s_1'$, respectively, the above results show that in many settings, the same representative is chosen. However, suppose, instead, FDR picks $s_2'$ as the representative of its bisimilarity equivalence class. Now, when we calculate the representative of the state $\sigma ''$ that contains $s_2'$ instead of $s_1'$, we might well obtain a different representative: the algorithm may be working with a completely different control state and variable binding.

The effect of this is that slightly more states are explored than if the compression and symmetry combined perfectly; however, the effect is rather small, normally less than 1%. Further, the number of states can vary slightly from one run to another: FDR may choose different representatives for a particular bisimilarity equivalence class on different runs.

7.5 Implementation considerations and alternatives

Calculating the n-values is a potentially expensive part of the implementation. We outline our approach. We start by calculating, for each value v of a distinguished type, the set

$$\begin{aligned} B(v)= & {} \{ (s,i) \mid s \in S,\, i \hbox { is an index of a variable of } s \\&\qquad \hbox { with }s(v_i) = v \} . \end{aligned}$$

We call B(v) a bucket. All the buckets can be efficiently calculated by calculating a vector of $(s,i,s(v_i))$ tuples and then sorting and partitioning by the third component. This can be done in time $O(N \log N)$ where N is the total number of variables in the states.

Then to calculate the n-values, we iterate over each bucket B(v), and for each $(s,i), (s',k) \in B(v)$, increment $n_{i,j,k}(s)$, where j is the index in the partition of $s'$. This takes time $O(\sum _v (\# B(v))^2)$. In practice, the buckets tend to be fairly small.

We intend to investigate alternatives to our definition of the n-values, which might not give such a large reduction in the state space, but that can be calculated more quickly, and hence give an overall reduction in checking time. Consider

$$\begin{aligned} n'_{i,j,k}(s)= & {} \hbox {if }~ \exists s' \in S_j \cdot s'(v_k) = s(v_i) \hbox {then }1 \hbox {else }0 . \end{aligned}$$

For each s and $s'$, the vector of values of $s'(v_k) = s(v_i)$ (as i and k vary) can be pre-calculated and stored as a bit map. Calculating $n'(s)$ can then be performed as a sequence of bit-wise operations. In the typical case that each bit map fits into a single word (i.e. the number of pairs of variables of the same type is at most 32) this can be done in O(n) operations.

Now consider

$$\begin{aligned} n''_j(s)= & {} \# \{ s' \in S_j \mid \exists i, k \cdot s'(v_k) = s(v_i) \} . \end{aligned}$$

For each s and $s'$, the value of $\exists i, k \cdot s'(v_k) = s(v_i)$ can be pre-calculated and stored. The value of $n''(s)$ can then be calculated in O(n) operations. Curiously, for a linked list with no external references, the algorithm will not necessarily give unique representatives, since it will fail to distinguish a linked list from its reversal; however, a more realistic example would have an external reference to the first node, breaking this symmetry.

7.6 Comparisons

In [3], Bošnački et al. define several strategies for producing representative functions. We discuss the two main ones here. Each strategy assumes that, for each symmetric type T, there is a family of symmetric components that are indexed by T; thus, for our running example, they could be used with the types NodeID and ThreadID, using the families of Node and Thread components, respectively, but they could not be used with the type Data.

• The sorted strategy sorts the family of component states by their nondistinguished parts (i.e. effectively step 1 of Definition 36); this then generates a permutation on the type, which is applied to all the components to generate the representative. If two components have the same nondistinguished parts, they will be ordered arbitrarily in the initial sorting; this gives nonunique representatives. This can work poorly in our setting, because we often have components with the same nondistinguished parts.

• The segmented strategy considers all permutations of the distinguished variables that would sort the component states by nondistinguished parts; it then picks the one that produces the lexicographically smallest state. Thus, this gives unique representatives. This works poorly in our setting, particularly with large values of the distinguished types, because there are too many such permutations to consider.

We perform an experimental comparison between these algorithms and our own in the next section.

Sistla et al. [38] employ an algorithm rather similar to ours, although their aim is to test whether two given states s and $s'$ are symmetric rather than to find a representative. They use the naive refinement algorithm of [1] (cf. the first two steps of Definition 36) on each of s and $s'$ until a fixed point is reached. They then try to generate a permutation $\pi$ to match the states, pairing components in corresponding multisets; for nonsingleton multisets produced by the first phase, the relevant parts of the permutation are generated randomly. They then test whether $\pi$ does indeed relate the two states.

This may falsely report that two states are not symmetric. In particular, this can happen in cases where our approach finds unique representatives. For example, suppose s and $s'$ each correspond to two linked lists, each of length two. The first phase will, for each state, partition the nodes into those that are the first and second nodes of their lists. Then the second phase will report the states to be symmetric only if the randomly generated permutation happens to pair off the correct states. By contrast, step 3 of our component ordering algorithm will split one of the multisets in an implementation-dependent way, but subsequently step 2 will split the other multiset in a compatible way.

Junttila [23] describes three algorithms for testing whether two states are symmetric. One algorithm converts the problem into that of testing whether two graphs are isomorphic; this is believed to be a difficult problem, and so the running times of the algorithm are quite high. The second algorithm considers an ordered partition of each type (compared with our ordered partition of component states). The ordered partition is refined according to various invariants: refinements that respect symmetries of the system. Various invariants are presented; we believe that steps 1 and 2 of our component ordering algorithm could also be presented as invariants. However, when no further invariant can be applied, all permutations that respect the partition are considered; thus, there is no counterpart of step 3 of our algorithm, which is crucial to our obtaining unique representatives in many cases. For example, in our linked list example, if there are k free nodes, the algorithm of [23] would consider k! permutations. The third algorithm does have a counterpart of our step 3, but considers all ways of splitting a single element from a particular set. In some cases, this reduces the number of permutations that subsequently have to be considered, but not in the above case of k free nodes.

Other approaches, e.g. [10, 25], also consider all permutations (either explicitly or implicitly), so as to find unique representatives, at the cost of an exponential blow-up.

Iosif [18] considers symmetry reduction in the context of heap-based programs, within the dSPIN checker. This approach finds unique representatives under the assumption that every location is reachable by following references from state variables, a result comparable to our Lemma 53.

Leuschel and Massart [26] consider symmetry reduction in the context of B models. They compute symmetry markers for states, with the property that symmetric states receive the same marker, but not necessarily the other way round; they then treat states with the same marker as being symmetric. Thus their approach provides a falsification algorithm, rather than a verification algorithm. Their approach has some similarities with ours in that it captures information about how values are related to one another in a state.

Babai and Kučera [2] show that just three steps of the naive refinement algorithm applied to a random graph with n nodes fail to produce a canonical form with probability $(o(1))^n$. This result is not directly applicable to our setting, since we do not deal with random graphs; however, it does suggest that the approach works well.

8 Experiments

We have implemented the techniques described earlier within FDR4. Refinement assertions can be annotated to require symmetry reduction. For each datatype, FDR identifies the largest subtype for which the script is constant-free, and performs symmetry reduction over the union of these subtypes. Alternatively, the user may explicitly give the subtypes over which symmetry reduction should be performed; in this case, FDR checks that the script is indeed constant-free for these subtypes. (If an assertion is not tagged in this way, the normal algorithm is run, so the symmetry reduction gives no overhead in this case.)

Table 1 Experimental results, without and with symmetry reduction, giving the number of states explored and time taken (excluding compilation time)

Table 1 gives results of experiments run to assess the benefits of symmetry reduction.⁸ The experiments were performed on a 32-core server (two 2.1GHz Intel(R) Xeon(R) E5-2683 CPUs with hyperthreading enabled, with 256GB of RAM). The example are as follows.

• ListStack represents the linked list-based implementation of a stack using locking, from the Introduction. The parameters represent the number of nodes in the linked list, the number of threads and the number of data values.

• TreeBroadcast is a model of a network routing algorithm. A collection of nodes, with one distinguished sender, grows a spanning tree of the network and then uses it to broadcast messages. The parameters are the number of nodes excluding the sender and the number of data values.

• DiningPhilosophers is a variant of the dining philosophers problem which uses a “butler” process, who does not allow all the philosophers to sit down simultaneously, so as to avoid deadlock. The parameter is the number n of philosophers. Each philosopher and fork have an identity (of the same type). In the first n steps, the philosophers nondeterministically choose their position at the table. The effect of symmetry reduction is to identify states that are equivalent up to rotations: thus the approach identifies the rotational symmetry of the system.

• LockFreeQueue is the model from [28] of the lock-free queue from [30]. The parameters are as for ListStack.

• CoarseGrainedListSet is the model of a linked list-based implementation of a set from [4]; the implementation, based on [16, Section 9.4], orders nodes by a hash of their datums and uses coarse-grained synchronisation. The parameters are the numbers of nodes and threads. (This system is not symmetric in the type of data, because of the use of the hash function; however, we use the same number of data values as nodes in each case.)

• FineGrainedListSet is the model of a fine-grained linked list-based implementation of a set from [4]; the implementation, based on [16, Section 9.5], associates a lock with each node. The parameters are as for CoarseGrainedListSet.

• ArrayQueue is the model of an array-based queue from [20], based on [8]. The parameters are the numbers of threads, data values, sequence numbers on “head” and “tail” references into the array and sequence numbers on data in the array.

• Peterson is Peterson’s mutual exclusion algorithm [29]. The parameter is the number of processes seeking entry to the critical section.⁹

• Database is an example of database managers from [40]. The parameter is the number of database managers.

In the latter four cases, the refinement checks tested whether the datatypes were linearisable [17]: whether the operations seem to take place one at a time, each between the time at which it is called and when it returns.

Table 2 Experimental results, comparing with the sorted and segmented strategies

Some models needed to be adapted slightly to make them symmetric. For example, LockFreeQueue used a particular node as an initial dummy header node and a particular data value for it. In order to avoid using constants (to satisfy Definition 23) we adapted the script to model a constructor process (analogous to the constructor of an object) that initialises the dummy header node, picking the node and its initial data value nondeterministically. (Figures in Table 1 without symmetry reduction are for the initial script, which was optimised for that case.) Similarly, as discussed above, in the dining philosophers example, the model started by constructing the ring of philosophers and forks. We believe that similar techniques can be used in other settings where the initial state is not fully symmetric.

Speed-ups are considerable, often two or three orders of magnitude. More importantly, we can now check much larger systems than previously. For the LinkedList example without symmetry reduction, it is easy to see that the number of states with parameters (n, t, 2) grows at least proportional to $n!\times 2^n$; hence, the case for (19,4,2) would have at least $3.8 \times 10^{26}$ states (extrapolating from the (7,4,2) case), which would be too large to check by a factor of more than $10^{16}$.

In the dining philosophers example, the reduction in state space is almost exactly equal to the number n of philosophers. Performing symmetry reduction means that FDR takes longer per state, so in fact the check with $n = 12$ takes longer with symmetry reduction than without it. However, the symmetry reduction does make it possible to analyse larger systems.

The use of symmetry reduction makes very little difference to memory consumption in FDR. Most importantly the number of bytes used to store each state during the main model checking phase is identical. There is a small overhead of storing datatypes concerning symmetry reduction for the components of the supercombinator, but this is normally negligible. Of course, the reduction in the number of states explored can give a huge reduction in memory consumption. By contrast, more memory is used during the compilation phase (which creates the supercombinator, normalises the specification, and does other precomputations) with symmetry reduction than without: FDR has to record for each state the values of all variables, which can increase memory consumption on this phase by up to a factor of 5. However, the memory usage on this phase is still normally much less than on the main checking phase.

8.1 Comparison with the sorted and segmented techniques

Table 2 gives results of an experimental comparison between our technique for finding representatives (Sect. 7), and the sorted and segmented techniques from [3] (Sect. 7.6), which we have also implemented within FDR.

Recall that the sorted and segmented techniques can perform symmetry reduction only for types that index a family of processes. They cannot, therefore, be used to perform symmetry reduction over the type of data values. In order to allow for comparison, we have therefore not performed reduction over this type (contrast with Table 1).

These experiments suggest that the segmented approach is considerably slower than our own approach, often by two orders of magnitude: recall that this approach considers all permutations of the datatype: the cost of doing so is just too great. It is noticeable that the state counts are often very similar to our own. The segmented approach finds unique representatives,¹⁰ so this suggests that we normally find unique representatives.

We would expect that other approaches that find unique representatives by considering all permutations, e.g. [10, 25], would behave similarly to the segmented approach.

The sorted approach works better than the segmented approach. On small examples, it tends to explore more states than our approach, but take less time: it is a simpler algorithm than ours, so takes less time on each state. However, with larger examples—where speed-ups are more important—our approach tends to be faster: our approach seems to scale better, giving proportionately larger reductions in states in these cases. Further, our technique completes on several examples where the segmented approach runs out of memory. Finally, on examples that make significant use of a symmetric type of data (ListStack, LockFreeQueue and ArrayQueue), our approach where we perform reduction on that type (Table 1) is faster that the segmented case, except on some very small examples.

9 Conclusions

In this paper we have presented an extension to FDR4 that exploits symmetry in the system. The basic idea is to factor the transition system with respect to permutation bisimilarity, picking a representative member of each equivalence class. We have presented refinement checking algorithms based on this technique and shown how to extract informative counterexamples when the refinement does not hold. Whereas several previous approaches to symmetry reduction have assumed that every state of the specification automaton (or every sub-formula of the specification formula) is symmetric, we need make no such assumption.

We have shown how to apply this within the powerful and general supercombinator framework used by FDR: we have shown how to verify that a supercombinator induces a symmetric LTS, and how to apply a permutation to a state of that LTS; the same techniques could be applied in other process algebraic settings.

We have presented a general syntactic result showing that a process is symmetric with respect to a datatype, subject to fairly general assumptions, principally that the script contains no constants of that type. $\hbox {CSP}_M$ is a large language, which makes it convenient for modelling purposes, but considerably complicates reasoning about the language.

We have presented a novel technique for calculating representatives of equivalence classes, and given evidence that it often finds unique representatives. The technique should be applicable in other similar system models, where each system state comprises component states with variables holding values of the symmetric types.

Finally we have carried out experiments that demonstrate the efficacy of our approach. In particular, the results show that our technique for finding representatives works better in practice than previous techniques, particularly for larger examples; further, our technique allows for symmetry reduction over a type that does not index a family of processes, such as the type of data.

It would be possible to further improve the performance of the symmetry implementation in FDR by making the $\hbox {CSP}_M$ evaluator aware of the symmetries. For example, suppose P(x) denotes a symmetric process over the type T: the current FDR evaluator will evaluate P(x) for each member x of T, even though it would be sufficient to evaluate P(x) for a single x. Extending the evaluator to exploit such symmetries is left as future research.

We believe that our implementation of symmetry reduction can be used to analyse a wide range of systems. Whenever a system is structurally symmetric, the corresponding LTS is also symmetric. Thus it can be applied to a wide class of concurrent algorithms and distributed systems. Further, when a system uses data with no distinguished values, then the induced LTS is symmetric in the type of that data.

Appendices

Appendix A: Generalised labelled transition systems

In the body of the paper, we used labelled transition systems (LTSs). These are sufficient for model checking in the traces model.

Recall that when model checking we normalise the transition system for the specification, so each resulting state may correspond to a set of states of the original LTS. However, when using the stable failures or failures–divergences models, in order for the semantics to be preserved, the states of the normalised LTS need to be labelled with additional information.

Likewise, FDR can perform various compressions upon LTSs. These compressions often remove $\tau$-transitions and merge states. Each state that is formed by applying a compression might again correspond to a set of states of the original LTS and so again needs to be labelled with additional information.

Below, we present generalised labelled transition systems (GLTSs), which contain this additional information. In “Symmetric GLTSs” appendix section, we adapt the definition of permutation bisimilarity to GLTSs. Then in “Appendix B” we describe how to adapt model checking to use GLTSs and, in particular, describe how to adapt the algorithm from Fig. 6 to the stable failures and failures–divergences models.

We say that a state is stable if no internal $\tau$ transition is possible. We say that a state stably accepts some set E of events if the state is stable, and all the events of E can be accepted (and no more).

Definition 54

A generalised labelled transition system (GLTS) is a tuple $L = (S, \varDelta , init, {\textsf {minaccs}}, \mathsf{div})$, where $(S, \varDelta , init)$ is an LTS, and

• ${\textsf {minaccs}}: S \mathbin {\rightarrow }\mathbf{P }(\mathbf{P }{\varSigma ^{\surd }})$ gives the minimal acceptances of a state: those sets E that can be stably accepted, and such that no proper subset of E can be stably accepted.

• $\mathsf{div}: S \mathbin {\rightarrow }Bool$ indicates whether the process can immediately diverge from this state, i.e. perform an infinite number of internal (hidden) events without any intervening visible events.

Note that ${\textsf {minaccs}}$ returns a set of acceptances, one for each constituent state. For example, if we normalise the process as in Fig. 3, the initial state would have minimal acceptances $\{\{a\}, \{b\}\}$. In practice, when working in the traces model we can omit the ${\textsf {minaccs}}$ and $\mathsf{div}$ components from a GLTS, and when working in the stable failures model we can omit the $\mathsf{div}$ component.

Most of the results in these appendices will deal with GLTSs; the following lemma will allow these results to be applied also to LTSs.

Lemma 55

An LTS $(S, \varDelta , init)$ can be interpreted as a GLTS $(S, \varDelta , init, {\textsf {minaccs}}, \mathsf{div})$ where

• ${\textsf {minaccs}}(s) = \{\}$ if $s \xrightarrow {\tau }$; and otherwise ${\textsf {minaccs}}(s) = \{\{ a \mid s \xrightarrow {a}\}\}$.

• $\mathsf{div}(s)$ holds iff there is an infinite path of $\tau$-transitions starting at s.

Let s be a state of a GLTS. We say that X is stably refused in s, denoted $s \,\mathsf{ref}\,X$, if s has some minimal acceptance that includes no event of X; i.e. no event from X is available, in some stable state:

$$\begin{aligned} s \,\mathsf{ref}\,X\iff & {} \exists A \in {\textsf {minaccs}}(s) \cdot A \cap X = \{\}. \end{aligned}$$

A stable failure of a process P is a pair (tr, X), which represents that P can perform the trace tr and then stably refuse X. We can then define the traces, stable failures, divergences and full failures of a state s of a GLTS.

If L is a GLTS, we will write traces(L) for the traces of the initial state of L, and similarly for failures and divergences.

Let S and I be GLTSs, representing a specification and implementation, respectively. We define refinement between S and I in the three main models of CSP as follows.

$$\begin{aligned}&S \sqsubseteq _T I iff traces(S) \supseteq traces(I), \\&S \sqsubseteq _F I iff traces(S) \supseteq traces(I) \\&\qquad \wedge failures(S) \supseteq failures(I), \\&S \sqsubseteq _{FD} I iff failures_{\mathord {\perp }}(S) \supseteq failures_{\mathord {\perp }}(I) \\&\qquad \wedge divs(S) \supseteq divs(I). \end{aligned}$$

FDR translates CSP processes into GLTSs and then tests for the above refinements.

1.1 A.1 Symmetric GLTSs

We adapt the definition of permutation bisimilarity (Definition 9) to GLTSs, to take account of minimal acceptances and divergences.

Definition 56

(Permutation bisimilarity) Let

$$\begin{aligned} L_1= & {} (S_1, \varDelta _1, init_1, {\textsf {minaccs}}_1, \mathsf{div}_1), \\ L_2= & {} (S_2, \varDelta _2, init_2, {\textsf {minaccs}}_2, \mathsf{div}_2) \end{aligned}$$

be GLTSs, and let $\pi \in G$ be an event permutation. We say that $\mathord {\sim } \subseteq S_1 \times S_2$ is a $\pi$-bisimulation between$L_1$and$L_2$ iff whenever $(s_1, s_2) \in \mathord {\sim }$ and ${a \in {\varSigma ^{\tau \surd }}}$:

• If $s_1\xrightarrow {a} s_1'$ then $\exists s_2' \in S_2 \cdot s_2 \xrightarrow {\pi (a)} s_2' \wedge s_1' \sim s_2'$;

• If $s_2 \xrightarrow {a} s_2'$ then $\exists s_1' \in S_1 \cdot s_1 \xrightarrow {\pi ^{-1}(a)} s_1' \wedge s_1' \sim s_2'$;

• $$\begin{aligned}&{\textsf {minaccs}}_2(s_2) \\&\qquad = \{\{\pi (a) \mid a \in A\} \mid A \in {\textsf {minaccs}}_1(s_1)\}; \end{aligned}$$

• $\mathsf{div}_1(s_1) \iff \mathsf{div}_2(s_2)$.

We say that $s_1, s_2 \in S$ are $\pi$-bisimilar, denoted $s_1 \sim _\pi s_2$ iff there exists a $\pi$-bisimulation relation $\sim$ such that $s_1 \sim s_2$. We say that $L_1$ and $L_2$ are $\pi$-bisimilar, denoted $L_1 \sim _\pi L_2$, iff $init_1 \sim _\pi init_2$.

The remainder of the definitions and lemmas of Sect. 2.3 carries across to GLTSs. In addition, the following lemma is easily proved from the definition.

Lemma 57

Suppose $s \sim _\pi s'$. Then

$$\begin{aligned} s \,\mathsf{ref}\,X\iff & {} s' \,\mathsf{ref}\,\pi (X). \end{aligned}$$

Appendix B: Refinement checking algorithms using GLTSs

In this section, we explain how to adapt the model checking algorithm for the traces model (Sect. 3.4) to GLTSs. We then present model checking algorithms for the stable failures and failures–divergences models.

We adapt the definitions of normalisation and the product automaton from Sect. 2.1 to GLTSs.

Definition 58

Given a GLTS $L = (S, \varDelta , init, {\textsf {minaccs}}, \mathsf{div})$, its prenormal form is a GLTS $N = ({\mathbf{P }S - \{\{\}\}}, \varDelta _N, init_N, {\textsf {minaccs}}_N, \mathsf{div}_N)$ defined as follows. Each state is a nonempty element of $\mathbf{P }S$. The initial state and the transition relation are defined as in Definition 3. For each state ${\hat{s}} \in \mathbf{P }S - \{\{\}\}$:

• ${\textsf {minaccs}}_N({\hat{s}}) = mins(\bigcup \{{\textsf {minaccs}}(s) \mid s \in {{\hat{s}}}\})$, where mins returns the $\subseteq$-minimal elements of its argument.

• $\mathsf{div}_N({\hat{s}}) \iff \exists s \in {\hat{s}} \cdot \mathsf{div}(s)$.

The normal form for L, denoted norm(L), is calculated by taking the prenormal form for L, restricting to reachable states, and then factoring by strong bisimulation, taking into account the divergences and minimal acceptances information. Given an LTS L, the normal form for L is calculated by first considering L as a GLTS, as in Lemma 55, and then applying the above construction.

Definition 59

Let $P = (S_P, \varDelta _P, init_P, {\textsf {minaccs}}_P, \mathsf{div}_P)$ be a normalised GLTS, and $Q = (S_Q, \varDelta _Q, init_Q, {\textsf {minaccs}}_Q, \mathsf{div}_Q)$ be a GLTS. The product automaton of P and Q is a tuple $(S, \varDelta , init, {\textsf {minaccs}}_P, \mathsf{div}_P, {\textsf {minaccs}}_Q, \mathsf{div}_Q )$ where S, $\varDelta$ and $init$ are as in Definition 6.

The lemmas from Sect. 2.3 concerning normalisation and the product automaton carry across to GLTSs in the obvious way. Likewise, the definitions and lemmas from Sect. 3 are adapted to GLTSs in the expected way. In particular, below we will make use of the adapted version of Lemma 20. The traces model checking algorithm from Fig. 6 can then be used directly, but taking GLTSs rather than LTSs.

For the remainder of this section, let $P = (S_P, \varDelta _P, init_P, {\textsf {minaccs}}_P, \mathsf{div}_P)$ be a normalised G-symmetric GLTS, $Q = (S_Q, \varDelta _Q, init_Q, {\textsf {minaccs}}_Q, \mathsf{div}_Q)$ be a G-symmetric GLTS, rep be a G-representative function on Q, S be the standard product automaton of P and Q, and R the reduced product automaton of P and Q.

We now consider refinement in the stable failures model. The following proposition shows how stable failures refinements are exhibited in the reduced product automaton.

Proposition 60

$P \sqsubseteq _F Q$ iff

Proof

($\Rightarrow$) We prove the contrapositive. Suppose

If , then the proof is as for Proposition 21. So suppose

$$\begin{aligned} \hat{q}\,\mathsf{ref}\,_Q X \wedge \lnot \hat{p}\,\mathsf{ref}\,_P X . \end{aligned}$$

Then by Lemma 20 (adapted to GLTSs), there exist a trace $tr'$, states p and q, and $\pi \in G$ such that

Now $\hat{q}\,\mathsf{ref}\,_Q X$, so $q \,\mathsf{ref}\,_Q \pi ^{-1}(X)$ by Lemma 57. And similarly $\lnot \hat{p}\,\mathsf{ref}\,_P X$ so $\lnot p \,\mathsf{ref}\,_P \pi ^{-1}(X)$. Hence

$$\begin{aligned} (tr' \ \tau , \pi ^{-1}(X))\in & {} failures(init_Q) \setminus failures(init_P), \end{aligned}$$

(by the uniqueness of the state of P reached after $tr'$). Hence $P \not \sqsubseteq _F Q$.

($\Leftarrow$) We prove the contrapositive. Suppose $P \not \sqsubseteq _F Q$. If this corresponds to there being a trace of $init_Q$ that is not a trace of $init_P$, then the proof is as in Proposition 21. So suppose

Then by Lemma 20, there exist a trace tr, states $\hat{p}$ and $\hat{q}$, and $\pi \in G$ such that

But then $\hat{q}\,\mathsf{ref}\,_Q \pi (Y) \wedge \lnot \hat{p}\,\mathsf{ref}\,_P \pi (Y)$ by Lemma 57. Letting $X = \pi (Y)$ we have the result. $\square$

It is straightforward to adapt the model checking algorithm from Fig. 6, and the counterexample reconstruction algorithm from Fig. 7, to the stable failures model. The only change necessary to the model checking algorithm is to replace the condition leading to a nonrefinement by

Note that the latter disjunct is equivalent to

$$\begin{aligned} \exists A \in {\textsf {minaccs}}_Q({\hat{q}}) \cdot \forall A' \in {\textsf {minaccs}}_P({\hat{p}}) \cdot A' \not \subseteq A. \end{aligned}$$

We now consider refinement in the failures–divergences model.

Proposition 61

$P \sqsubseteq _{FD} Q$ iff

Proof

($\Rightarrow$) We prove the contrapositive. Let tr be the shortest trace that makes the right-hand side false. So

So necessarily $init_P$ does not diverge after tr or any prefix of it; and necessarily $init_Q$ does not diverge on any proper prefix of tr, by the presumed minimality of tr.

• If $\exists X \in \mathbf{P }{\varSigma ^{\surd }}\cdot \hat{q}\,\mathsf{ref}\,_Q X \wedge \lnot \hat{p}\,\mathsf{ref}\,_P X$, the proof is as for Proposition 60.

• If $\mathsf{div}_Q \hat{q}$, then by Lemma 20, there exist a trace $tr'$, states p and q, and $\pi \in G$ such that

  

  But then $\mathsf{div}_Q q \wedge \lnot \mathsf{div}_P p$. Hence

  $$\begin{aligned} tr' \ \tau\in & {} divs(init_Q) \setminus divs(init_P), \end{aligned}$$

  (by the uniqueness of the state of P reached after $tr'$). Hence $P \not \sqsubseteq _{FD} Q$.

($\Leftarrow$) We again prove the contrapositive. Suppose $P \not \sqsubseteq _{FD} Q$.

• Suppose $divs(init_Q) \not \subseteq divs(init_P)$. Then there exists a trace $tr' \in {\varSigma ^{\tau \surd }}^*$ and states p and q such that

  

  By Lemma 20, there exist a trace tr, states $\hat{p}$ and $\hat{q}$, and $\pi \in G$ such that

  

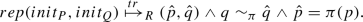
  But then $\mathsf{div}_Q \hat{q}\wedge \lnot \mathsf{div}_P \hat{p}$, as required.

• Suppose $divs(init_Q) \subseteq divs(init_P)$ but

  $$\begin{aligned} failures_{\mathord {\perp }}(init_Q)&\not \subseteq&failures_{\mathord {\perp }}(init_P). \end{aligned}$$

  Then there exist $tr' \in {\varSigma ^{\tau \surd }}^*$, refusal $Y \in \mathbf{P }{\varSigma ^{\surd }}$, and states p and q such that

  

  Then by Lemma 20, there exist a trace tr, states $\hat{p}$ and $\hat{q}$, and $\pi \in G$ such that

  

  But then $\hat{q}\,\mathsf{ref}\,\pi (Y) \wedge \lnot \mathsf{div}_P \hat{p}\wedge \lnot \hat{p}\,\mathsf{ref}\,\pi (Y)$. Letting $X = \pi (Y)$, we have the result.

$\square$

It is again straightforward to adapt the model checking and counterexample reconstruction algorithms to the failures–divergences model. The condition leading to a nonrefinement is changed to

$$\begin{aligned} \begin{aligned}&\lnot \mathsf{div}_P \hat{p}\wedge \\&( (\exists X \in \mathbf{P }{\varSigma ^{\surd }}\cdot \hat{q}\,\mathsf{ref}\,_Q X \wedge \lnot \hat{p}\,\mathsf{ref}\,_P X) \vee \mathsf{div}_Q \hat{q}) . \end{aligned} \end{aligned}$$

Appendix C: Symmetry reduction on generalised supercombinators

In the body of the paper, we gave a slightly simplified presentation of supercombinators, in the interests of explaining the main ideas without getting bogged down in the details. In this appendix and the next, we extend the results to more general supercombinators.

The simplified supercombinators had a single format, which is appropriate when the construction of the system is static, i.e. the same processes are running (“on”) in each state. However, consider a process such as

Suppose this is implemented using a supercombinator with three components, corresponding to P, Q and R. This naturally has three formats:

• In the initial format, no component is on; the system has two $\tau$-transitions, resolving the nondeterministic choice, and leading to the two subsequent formats.

• If the nondeterministic choice is resolved to the left, the system subsequently behaves like $P |||Q$: the components for P and Q are on, but the component for R is off.

• If the nondeterministic choice is resolved to the right, the system subsequently behaves like $R \ X$: the component for R is on, but the components for P and Q are off.

Different supercombinator rules apply in the different formats. Hence there is no way to model this system using a simplified supercombinator with P, Q and R as its components: the only option would be to compile the whole system into a single component, which would be very expensive.

In addition, there are circumstances under which it is necessary to reset a process to its initial state, in order to model recursion. And we allow a component to be a GLTS, rather than necessarily an LTS, in order to deal with compression functions. We explain each of these points below.

Definition 62

A generalised supercombinator is a 5-tuple $({\mathcal {L}}, F, {\mathcal {R}}, on, f_0)$ where

• ${\mathcal {L}} = \langle L_1, \ldots , L_n\rangle$ is a sequence of component GLTSs.

• F is a finite set of formats.

• $on : F \mathbin {\rightarrow }\mathbf{P }\{1,\ldots ,n\}$ indicates, for each format, which of the component GLTSs are on.

• ${\mathcal {R}}$ is a function from formats to sets of supercombinator rules. For each $f \in F$,  ${\mathcal {R}}(f)$ is a finite set of supercombinator rules $(e, a, r, f')$ where

  • $e \in (\varSigma ^-)^n$ specifies the action each on component must perform, where − indicates that it performs none; if $e(i) \ne \mathord {-}$ then $i \in on(f)$.

  • $a \in \varSigma$ is the event the supercombinator performs.

  • $r \subseteq \{1,\ldots , n\}$ are the indices of the components from ${\mathcal {L}}$ that are reset.

  • $f' \in F$ is the subsequent format.

• $f_0 \in F$ is the initial format.

In these appendices, we often say “supercombinator” to mean a generalised supercombinator.

In FDR, a component GLTS can be implemented in one of three ways:

• As a low-level LTS, explicitly listing the transitions for each state, and interpreted as a GLTS, as in Lemma 55. This is the default, and will be the case when no compression operators are involved.

• As a low-level GLTS, explicitly listing the transitions, minimal acceptances and divergence information for each state. This results from application of certain compression functions. FDR automatically compresses leaf components, merging states that are strongly bisimilar: this is known as leaf compression. Alternatively, this GLTS might have been obtained by compressing another supercombinator: in this case, each state of the low-level GLTS will correspond to a state of the nested supercombinator.

• As a lazy enumerated GLTS, calculating transitions as needed. This results from compression functions such as lazyenumerate, chase and prioritise. The lazy enumerated GLTS might be formed by wrapping a nested supercombinator; in this case, each state of the GLTS will again correspond to a state of the nested supercombinator.

Given a supercombinator, a corresponding GLTS can be constructed.

Definition 63

Let ${\mathcal {S}} = (\langle L_1, \ldots , L_n\rangle , F, {\mathcal {R}}, on, f_0)$ be a supercombinator where $L_i = (S_i, \varDelta _i, init_i, {\textsf {minaccs}}_i, \mathsf{div}_i)$. The GLTS induced by${\mathcal {S}}$ is the GLTS $(S, \varDelta , init, {\textsf {minaccs}}, \mathsf{div})$ such that:

• States are tuples consisting of the state of each component, plus the identifier of the format: $S \subseteq S_1 \times \cdots \times S_n \times F$.

• The initial state is the tuple containing the initial states of each of the components, along with the initial format: $init= (init_1, \ldots , init_n, f_0)$.

• The transitions correspond to the supercombinator rules firing. Let $\sigma = (s_1, \ldots , s_n, f)$, and $\sigma ' = (s'_1, \ldots , s'_n,f')$. Then $(\sigma , a, \sigma ') \in \varDelta$ iff there exists $((b_1, \ldots , b_n),a,r,f') \in \mathcal {R}(f)$ such that for each component i, there exists a state $s_i''$ such that

  • 1. If $b_i \ne -$ then $s_i \xrightarrow {b_i}_i s_i''$; and if $b_i = -$ then $s_i'' = s_i$; i.e. component i performs $b_i$, or does nothing if $b_i = \mathord -$;

  • 2. If $i \notin r$ then $s_i' = s_i''$; and if $i \in r$ then $s_i' = init_i$; i.e. the components in r are reset to their initial states.

• For each state $\sigma = (s_1,\ldots ,s_n,f)$ with $on(f) = \{i_1,\ldots ,i_k\}$:

  $$\begin{aligned} \begin{aligned}&{\textsf {minaccs}}(\sigma ) \\&\quad = mins \{join_f(X_{i_1},\ldots ,X_{i_k}) \mid \\&\qquad \qquad X_{i} \in {\textsf {minaccs}}_{i}(s_{i}) \hbox { for }i = i_1,\ldots ,i_k \}, \end{aligned} \end{aligned}$$

  where

  $$\begin{aligned}&join_f(X_{i_1},\ldots ,X_{i_k}) \\&\quad =\{ a \mid \exists ((e_1,\ldots ,e_n), a, r, f') \in {\mathcal {R}}(f) \cdot \\&\qquad \qquad \forall i \in \{i_1,\ldots ,i_k\} \cdot e_i \ne \_ \implies e_i \in X_i \}, \end{aligned}$$

  and mins returns the $\subseteq$-minimal elements of its argument.

• For each state $\sigma$,  $\mathsf{div}(\sigma )$ is true iff either:

  • from $\sigma$,  ${\mathcal {S}}$ can perform a finite sequence of $\tau$-transitions to some state $\sigma ' = (s_1,\ldots ,s_n,f)$ such that some on component can diverge, i.e. $\exists i \in on(f) \cdot \mathsf{div}_i(s_i)$; or

  • from $\sigma$,  ${\mathcal {S}}$ can perform an infinite sequence of $\tau$-transitions.

The generalisation of supercombinators makes it possible to define a supercombinator corresponding to each CSP operator and recursion. The following examples illustrate the ideas of multiple formats and resetting.

Example 64

Let $T = \{t_1,\ldots ,t_n\}$, and consider

The natural supercombinator would be $(\langle L_1, \ldots , L_n\rangle , \{f_0,\ldots ,f_n\}, {\mathcal {R}}, on, f_0)$, where

• $L_i$ is the LTS for $P(t_i)$.

• $f_0$ is the initial format, and for $i>0$,  $f_i$ is the format corresponding to the nondeterministic choice choosing $t_i$, so $on(f_0) = \{\}$ and $on(f_i) = \{i\}$ for $i>0$.

• The rules ${\mathcal {R}}$ are as follows. We write “$\mathord {-}^n$” for the tuple $(\mathord {-},\ldots ,\mathord {-})$ of size n, and “$e_i^a$” for the tuple with a in position i and $\mathord {-}$ elsewhere; then we have

  $$\begin{aligned} {\mathcal {R}} (f_0)= & {} \{ (\mathord {-}^n, \tau , \{\}, f_i) \mid i \in \{1,\ldots ,n\} \}, \\ {\mathcal {R}} (f_i)= & {} \{ (e_i^a, \hbox {if }a \in X(t_i) \hbox {then }\tau \hbox {else }a, \{\}, f_i) \mid \\&\qquad a \in {\varSigma ^{\tau \surd }}\}, \qquad i = 1,\ldots ,n. \end{aligned}$$

  The rule ${\mathcal {R}} (f_0)$ captures that the system can perform a $\tau$ (with no component changing state) and evolve into the state captured by format $f_i$. The rule ${\mathcal {R}} (f_i)$ captures that if the ith component can perform a transition labelled with a, then the system can perform a transition labelled with either $\tau$ or a (depending on whether $a \in X(t_i)$), and remain in the same format. In each case, no component is reset.

Example 65

Let P be a process that can perform $\surd$, indicating termination (and maybe other events), and let $Q = P ; Q$. Then the natural supercombinator for Q would have a single component LTS $L_1$, corresponding to P, and a single format $f_0$ such that $on(f_0) = \{1\}$, and

$$\begin{aligned} {\mathcal {R}} (f_0)= & {} \begin{aligned} \{ ((a), a, \{\}, f_0) \mid a \in {\varSigma ^\tau }\} \cup \{ ((\surd ), \tau , \{1\}, f_0) \} . \end{aligned} \end{aligned}$$

The last rule captures that if $L_1$ performs $\surd$, the $\surd$ is made internal (i.e. $\tau$), and $L_1$ is reset to its initial state.

The following example illustrates the way supercombinators can be nested.

Example 66

Let $T = \{t_1,\ldots ,t_n\}$, and consider the process

$$\begin{aligned} \begin{aligned} P =&|||_{t:T} compress ( Q(t) ), \\&\text{ where } \quad Q(t) = |||_{t':T} R(t,t'), \end{aligned} \end{aligned}$$

where compress is some compression function. FDR will normally implement each compress(Q(t)) as a component of the top-level supercombinator for P. Each such component is produced by compressing the GLTS of the supercombinator corresponding to Q(t) (and storing the transitions explicitly), so each state of that component contains a state for each sub-component $R(t,t')$. Thus each state of the supercombinator for P is of the form

$$\begin{aligned} \begin{aligned}&((s_{1,1},s_{1,2},\ldots ,s_{1,n},f_1),\; (s_{2,1},s_{2,2},\ldots ,s_{2,n},f_2),\; \ldots ,\; \\&\qquad (s_{n,1},\ldots ,s_{n,n},f_n),\; f) \end{aligned} \end{aligned}$$

where each $s_{i,j}$ is a state of $R(t_i,t_j)$.

1.1 C.1 Symmetries between generalised supercombinators

We now consider symmetries between supercombinators, and how these correspond to symmetries between the corresponding GLTSs. We are mainly interested in showing that the supercombinator corresponding to the implementation process in a refinement check is symmetric, i.e. $\pi$-bisimilar to itself for every event permutation $\pi$ in some group G. However, when several components of a supercombinator are implemented as nested supercombinators, we will sometimes want to show that one nested supercombinator is $\pi$-bisimilar to another, so we consider this generalisation.

We start by relating the component GLTSs of two supercombinators.

Definition 67

Consider two collections of GLTSs, $\mathcal {L} = \langle L_1, \ldots , L_n\rangle$ and $\mathcal {L'} = \langle L'_1, \ldots , L'_n\rangle$. Let $\pi$ be an event permutation, and let $\alpha$ be a bijection from $\{1,\ldots ,n\}$ to itself. We say that $\mathcal {L}$ is $\pi$-mappable to $\mathcal {L}'$using component bijection $\alpha$ if for every i,  $L_i \sim _\pi L'_{\alpha (i)}$.

We now consider how to relate the rules of two supercombinators. This is made harder by the presence of multiple formats. The following definition captures when two formats (maybe in different supercombinators) act in a similar way, but on different component GLTSs, and with events renamed under $\pi$. We will use this to identify when the supercombinators induce $\pi$-bisimilar GLTSs (Proposition 72).

Definition 68

Let $\pi$ be an event permutation. Let

${\mathcal {S}} = (\langle L_1, \ldots , L_n\rangle , F, {\mathcal {R}}, on, f_0)$ and ${\mathcal {S}}' = (\langle L'_1, \ldots , L'_n\rangle , F', {\mathcal {R}}', on', f'_0)$ be supercombinators whose component GLTSs are $\pi$-mappable with component bijection $\alpha$. Then a relation $\sim ^F$ over $F \times F'$ is a format$\pi$-bisimulation using $\alpha$ if whenever $f \sim ^F f'$:

• If $(e,a,r,f_1) \in {\mathcal {R}}(f)$ then there is a rule $(e',\pi (a), \alpha (r),f_1') \in {\mathcal {R}}'(f')$ such that

  $$\begin{aligned} \forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i)) \text{ and } f_1 \sim ^F f_1'. \end{aligned}$$

• If $(e',a,r,f_1') \in {\mathcal {R}}'(f')$ then there is a rule $(e, \pi ^{-1}(a), \alpha ^{-1}(r),f_1) \in {\mathcal {R}}(f)$ such that

  $$\begin{aligned} \forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i)) \text{ and } f_1 \sim ^F f_1'. \end{aligned}$$

• $\alpha (on(f)) = on'(f')$.

This says that f acts on each GLTS $L_i$ in the same way as $f'$ acts on $L'_{\alpha (i)}$, but with the latter’s events renamed under $\pi$.

Definition 69

Consider two supercombinators ${\mathcal {S}} = ({\mathcal {L}}, F, {\mathcal {R}}, on, f_0)$ and ${\mathcal {S}}' = ({\mathcal {L}}', F', {\mathcal {R}}', on', f'_0)$. Then ${\mathcal {S}}$ is $\pi$-mappable to${\mathcal {S}}'$using component bijection $\alpha$ if

• 1. ${\mathcal {L}}$ and ${\mathcal {L}}'$ are $\pi$-mappable using $\alpha$; and

• 2. There is a format $\pi$-bisimulation $\sim _\pi ^F$ over $F \times F'$ using $\alpha$ such that $f_0 \sim _\pi ^F f_0'$.

Example 70

Let $T = \{t_1,\ldots ,t_n\}$, and consider

Assume that the script is constant-free for T. The natural supercombinator ${\mathcal {S}}$ for this system was described in Example 64. Let $\pi$ be a permutation on T. Let component bijection $\alpha$ be such that $\alpha (i) = j$ when $\pi (t_i) = t_j$. We show that ${\mathcal {S}}$ is $\pi$-mappable to itself using $\alpha$.

By Proposition 24, $P(t_{\alpha (i)}) = \pi (P(t_i))$, so the GLTSs are $\pi$-mappable to themselves under $\alpha$. By the same proposition, $\pi (X(t_i)) = X(\pi (t_i))$. Define

$$\begin{aligned} \mathord {\sim _{\pi }^F}= & {} \{(f_0,f_0)\} \cup \{(f_i,f_{\alpha (i)}) \mid i \in \{1,\ldots ,n\}\}. \end{aligned}$$

We show that $\sim _\pi ^F$ is a format $\pi$-bisimulation. The relevant conditions on the rules are clearly satisfied by the pair $(f_0,f_0)$. For $i>0$, note that

$$\begin{aligned} \begin{aligned}&(e_i^a, b, \{\}, f_i) \in {\mathcal {R}}(f_i) \\&\qquad \iff (e_{\alpha (i)}^{\pi (a)}, \pi (b), \{\}, f_{\alpha (i)}) \in {\mathcal {R}}(\alpha (f_i)), \end{aligned} \end{aligned}$$

for each a, b, since

• If $a \in X(t_i)$ then $\pi (a) \in \pi (X(t_i)) = X(\pi (t_i)) = X(t_{\alpha (i)})$, and the two rules have $b = \pi (b) = \tau$;

• If $a \notin X(t_i)$, then similarly $\pi (a) \notin X(t_{\alpha (i)})$, and the two rules have $b = a$, and $\pi (b) = \pi (a)$, respectively.

Further, these rules correspond, as required by Definition 68; in particular $e_{\alpha (i)}^{\pi (a)}(\alpha (j)) = \pi (e_i^a(j))$ (since both sides equal $\pi (a)$ if $i = j$; and both equal − otherwise). Finally, $\alpha (on(f_i)) = \{\alpha (i)\} = on(f_{\alpha (i)})$. Clearly $f_0 \sim _\pi ^F f_0$. Hence ${\mathcal {S}}$ is $\pi$-mappable to itself, for each $\pi \in EvSym (T)$.

We now show that $\pi$-mappable supercombinators induce $\pi$-bisimilar GLTSs.

Lemma 71

Let $\pi$ be an event permutation, and let

$$\begin{aligned} \mathcal {S}= & {} (\langle L_1, \ldots , L_n\rangle , F, {\mathcal {R}}, on, f_0) \\ \mathcal {S'}= & {} (\langle L'_1, \ldots , L'_n\rangle , F', {\mathcal {R}}', on', f_0') \end{aligned}$$

be $\pi$-mappable supercombinators with component bijection $\alpha$ and format $\pi$-bisimulation $\sim _\pi ^F$. Consider the relation $\approx _\pi$ defined over states of the induced GLTSs by

$$\begin{aligned} \begin{aligned}&(s_1,\ldots ,s_n,f) \approx _\pi (s_1',\ldots ,s_n',f') \;\text{ iff }\; \\&\qquad (\forall i \in \{1,\ldots ,n\} \cdot s_i \sim _{\pi } s'_{\alpha (i)}) \wedge f \sim _\pi ^F f'. \end{aligned} \end{aligned}$$

Then $\approx _\pi$ is a $\pi$-bisimulation. Further, the initial states of the two GLTSs are related by $\approx _\pi$.

The proposition below follows easily from the above lemma.

Proposition 72

• 1. Suppose supercombinator ${\mathcal {S}}$ is $\pi$-mappable to supercombinator ${\mathcal {S}}'$. Then the induced GLTSs are $\pi$-bisimilar.

• 2. Suppose ${\mathcal {S}}$ is a supercombinator that is $\pi$-mappable to itself for every $\pi \in G$. Then the induced GLTS is G-symmetric.

Recall that a supercombinator might contain components that are implemented using nested supercombinators. Together, these supercombinators form a tree (but only to a finite depth). When a component is not implemented as a nested supercombinator, we call it a leaf.

In order to statically prove that two supercombinators, possibly with nested supercombinators, induce $\pi$-bisimilar GLTSs, we require a stronger condition, that descends through nested supercombinators, showing corresponding components are suitably related.

Definition 73

Consider two supercombinators

$$\begin{aligned} {\mathcal {S}}= & {} (\langle L_1, \ldots , L_n\rangle , F, \mathcal R, on, f_0), \\ {\mathcal {S}}'= & {} (\langle L'_1, \ldots , L'_n\rangle , F', {\mathcal {R}}', on', f'_0). \end{aligned}$$

Let $\pi$ be an event permutation, and let $\alpha$ be a bijection on $\{1,\ldots ,n\}$. Then ${\mathcal {S}}$is recursively$\pi$-mappable to${\mathcal {S}}'$using component bijection $\alpha$ if

• 1. For every $i \in \{1,\ldots ,n\}$, either

  • (a) $L_i$ and $L_{\alpha (i)}'$ are leaf GLTSs, and $L_i \sim _\pi L'_{\alpha (i)}$; or

  • (b) $L_i$ and $L_{\alpha (i)}'$ are nested supercombinators, and $L_i$ is recursively $\pi$-mappable to $L_{\alpha (i)}'$ using some component bijection $\alpha _i$.

• 2. There is a format $\pi$-bisimulation $\sim _\pi ^F$ over $F \times F'$ using $\alpha$ such that $f_0 \sim _\pi ^F f_0'$.

In “Appendix D” we will explain how to statically identify that two supercombinators are recursively $\pi$-mappable. The proposition below then shows that these supercombinators are $\pi$-bisimilar.

Proposition 74

• 1. Suppose supercombinator ${\mathcal {S}}$ is recursively $\pi$-mappable to supercombinator ${\mathcal {S}}'$. Then the induced GLTSs are $\pi$-bisimilar.

• 2. Suppose ${\mathcal {S}}$ is a supercombinator that is recursively $\pi$-mappable to itself for every $\pi \in G$. Then the induced GLTS is G-symmetric.

Proof

The proof of part 1 is by induction on the depth of the tree of nested supercombinators. Given ${\mathcal {S}}$ and ${\mathcal {S}}'$, the inductive hypothesis says that any corresponding components that are implemented as nested supercombinators have induced GLTSs that are $\pi$-bisimilar. Hence ${\mathcal {S}}$ and ${\mathcal {S}}'$ are $\pi$-mappable, and so, by Proposition 72, the induced GLTSs are $\pi$-bisimilar.

Part 2 then follows immediately. $\square$

Example 75

Let $T = \{t_1,\ldots ,t_n\}$. Consider, again, the process from Example 66:

$$\begin{aligned} \begin{aligned} P =&|||_{t:T} compress ( Q(t) ), \\&\text{ where } \quad Q(t) = |||_{t':T} R(t,t'). \end{aligned} \end{aligned}$$

Suppose the script is constant-free for T, and let $\pi \in EvSym(T)$. Let ${\mathcal {S}}$ be P’s supercombinator, and let ${\mathcal {S}}_i$ be the component of ${\mathcal {S}}$ corresponding to $compress(Q(t_i))$; recall that this is a nested supercombinator. Let the components of ${\mathcal {S}}_i$ be $\langle L_{i,1},\ldots ,L_{i,n}\rangle$. (Note that we make no assumption about the order of these components.) Let $\alpha$ be such that $t_{\alpha (i)} = \pi (t_i)$, for each i. Let $\alpha _i$ be such that if $L_{i,j}$ corresponds to $R(t_i, t')$ then $L_{\alpha (i), \alpha _i(j)}$ corresponds to $R(\pi (t_i), \pi (t'))$, for each j. Then, by Proposition 24, $L_{i,j} \sim _\pi L_{\alpha (i), \alpha _i(j)}$. It is then easy to show that ${\mathcal {S}}_i$ is recursively $\pi$-mappable to ${\mathcal {S}}_{\alpha (i)}$ using $\alpha _i$. (The natural supercombinator for each has a single format, and the rules satisfy the conditions for a format bisimulation.) Likewise, it is then easy to show that ${\mathcal {S}}$ is recursively $\pi$-mappable to itself using $\alpha$.

We now show that the property of supercombinators being recursively mappable is compositional in the obvious way. We start by showing how format bisimulations compose. Below we sometimes decorate the component bijections $\alpha$ with the corresponding event permutation and/or their source and target supercombinators.

Lemma 76

Consider three supercombinators

$$\begin{aligned} {\mathcal {S}}= & {} ({\mathcal {L}}, F, {\mathcal {R}}, on, f_0), \\ {\mathcal {S}}'= & {} ({\mathcal {L}}', F', {\mathcal {R}}', on', f_0'), \\ {\mathcal {S}}''= & {} ({\mathcal {L}}'', F'', {\mathcal {R}}'', on'', f_0''). \end{aligned}$$

Suppose $\sim _\pi ^F$ is a format $\pi$-bisimulation between ${\mathcal {S}}$ and ${\mathcal {S}}'$ using component bijection $\alpha _{\pi }^{{\mathcal {S}},{\mathcal {S}}'}$, and $\sim _{\pi '}^F$ is a format $\pi '$-bisimulation between ${\mathcal {S}}'$ and ${\mathcal {S}}''$ using component bijection $\alpha _{\pi '}^{{\mathcal {S}}',{\mathcal {S}}''}$. Then $\sim _\pi ^F ;\sim _{\pi '}^F$ is a format $(\pi ;\pi ')$-bisimulation between ${\mathcal {S}}$ and ${\mathcal {S}}''$ using component bijection $\alpha _\pi ^{{\mathcal {S}},{\mathcal {S}}'} ; \alpha _{\pi '}^{{\mathcal {S}}',{\mathcal {S}}''}$.

Proof

Suppose $f ~(\sim _\pi ^F ;\sim _{\pi '}^F)~ f''$. Then there is a format $f'$ such that $f \sim _\pi ^F f'$ and $f' \sim _{\pi '}^F f''$. We check the conditions for being a format $(\pi ;\pi ')$-bisimulation.

Suppose $(e,a,r,f_1) \in {\mathcal {R}}(f)$. Then, since $f \sim _\pi ^F f'$, there is a rule $(e',\pi (a), \alpha _\pi (r), f_1') \in {\mathcal {R}}'(f')$ such that $e'(\alpha _\pi (i)) = \pi (e(i))$ for each $i \in \{1,\ldots ,n\}$, and ${f_1 \sim _\pi ^F f_1'}$. But then, since $f' \sim _{\pi '}^F f''$, there is a rule $(e'',(\pi ;\pi ')(a), {(\alpha _{\pi } ;\alpha _{\pi '})}(r),f_1'') \in {\mathcal {R}}''(f'')$ such that $e''(\alpha _{\pi '}(i)) = \pi '(e'(i))$ for each i, and $f_1' \sim _{\pi '}^F f_1''$. Hence, for each i,  $e''((\alpha _\pi ;\alpha _{\pi '})(i)) = e''(\alpha _{\pi '}(\alpha _{\pi }(i))) = \pi '(e'(\alpha _\pi (i))) = (\pi ;\pi ')(e(i))$. And ${f_1 ~ (\sim _\pi ^F ;\sim _{\pi '}^F) ~f_1''}$, as required.

The reverse condition is very similar.

Finally, $\alpha _\pi (on(f)) = on'(f')$ and $\alpha _{\pi '}(on'(f')) = on''(f'')$, so $(\alpha _{\pi } ; \alpha _{\pi '})(on(f)) = on''(f'')$. $\square$

Lemma 77

Consider three supercombinators

$$\begin{aligned} {\mathcal {S}}= & {} ({\mathcal {L}}, F, {\mathcal {R}}, on, f_0), \\ {\mathcal {S}}'= & {} ({\mathcal {L}}', F', {\mathcal {R}}', on', f_0'), \\ {\mathcal {S}}''= & {} ({\mathcal {L}}'', F'', {\mathcal {R}}'', on'', f_0''). \end{aligned}$$

Suppose ${\mathcal {S}}$ is recursively $\pi$-mappable to ${\mathcal {S}}'$ using component bijection $\alpha _\pi ^{{\mathcal {S}},{\mathcal {S}}'}$, and ${\mathcal {S}}'$ is recursively $\pi '$-mappable to ${\mathcal {S}}''$ using component bijection $\alpha _{\pi '}^{{\mathcal {S}}',{\mathcal {S}}''}$. Then ${\mathcal {S}}$ is recursively $(\pi ;\pi ')$-mappable to ${\mathcal {S}}''$ using component bijection $\alpha _{\pi }^{{\mathcal {S}},{\mathcal {S}}'} ; \alpha _{\pi '}^{{\mathcal {S}}',{\mathcal {S}}''}$.

Proof

The proof is by induction on the depth of supercombinator nesting. We prove the result, following the structure of Definition 73.

• 1. Suppose ${\mathcal {L}}= \langle L_1,\ldots ,L_n\rangle$,  ${\mathcal {L}}' = \langle L_1',\ldots ,L_n'\rangle$ and ${\mathcal {L}}'' = \langle L_1'',\ldots ,L_n''\rangle$. Consider $L_i$,  $L_{\alpha _\pi (i)}'$ and $L''_{\alpha _{\pi '}(\alpha _\pi (i))}$. There are two possibilities:

  • (a) All three are leaf GLTSs, $L_i \sim _\pi L_{\alpha _\pi (i)}'$, and $L_{\alpha _\pi (i)}' \sim _{\pi '} L''_{\alpha _{\pi '}(\alpha _\pi (i))}$; hence $L_i \sim _{\pi ; \pi '} L''_{\alpha _{\pi '}(\alpha _\pi (i))}$.

  • (b) All three are nested supercombinators, $L_i$ is recursively $\pi$-mappable to $L_{\alpha _\pi (i)}'$, and $L_{\alpha _\pi (i)}'$ is recursively $\pi '$-mappable to $L''_{\alpha _{\pi '}(\alpha _\pi (i))}$. Then by the inductive hypothesis, $L_i$ is recursively $(\pi ;\pi ')$-mappable to $L''_{\alpha _{\pi '}(\alpha _\pi (i))}$.

• 2. By assumption, there is a format $\pi$-bisimulation $\sim _\pi ^F$ between ${\mathcal {S}}$ and ${\mathcal {S}}'$ using $\alpha _{\pi }$ such that $f_0 \sim _\pi ^F f_0'$; and there is a format $\pi '$-bisimulation $\sim _{\pi '}^F$ between ${\mathcal {S}}'$ and ${\mathcal {S}}''$ using $\alpha _{\pi '}$ such that $f_0' \sim _{\pi '}^F f_0''$. By Lemma 76, $\sim _\pi ^F ;\sim _{\pi '}^F$ is a format $(\pi ;\pi ')$-bisimulation between ${\mathcal {S}}$ and ${\mathcal {S}}''$ using $\alpha _\pi ; \alpha _{\pi '}$. And $f_0 ~(\sim _\pi ^F ;\sim _{\pi '}^F)~ f_0''$.$\square$

Appendix D: Identifying symmetries and applying permutations in generalised supercombinators

In this appendix, we extend the results and techniques of Sect. 6 to generalised supercombinators. Let ${\mathcal {T}}$ be a collection of datatypes. In “Checking recursive mappability” appendix section, we explain how we check that the supercombinator ${\mathcal {S}}_{impl}$ for the implementation is recursively $\pi$-mappable to itself for every $\pi \in EvSym({\mathcal {T}})$. We explain how to apply such an event permutation to a state of the supercombinator in “Applying permutations to states” appendix section.

1.1 D.1 Checking recursive mappability

We now explain how to check that ${\mathcal {S}}_{impl}$ is recursively $\pi$-mappable to itself, for every permutation $\pi$ of the distinguished types. Some parts are as in Sect. 6.1 so we just give an outline. By Lemma 77, it suffices to consider just permutations $\pi$ from a set of generators of the full symmetry group. Note, though, that if ${\mathcal {S}}_{impl}$ contains nested supercombinators, we might need to show that one component supercombinator ${\mathcal {S}}$ is recursively $\pi$-mappable to another ${\mathcal {S}}'$, so we consider this more general problem.

So consider two supercombinators

$$\begin{aligned} \begin{array}{rcll} {\mathcal {S}} &{} = &{} ({\mathcal {L}}, F, {\mathcal {R}}, on, f_0), &{} \quad \text{ with } {\mathcal {L}}= \langle L_1,\ldots ,L_n\rangle , \\ {\mathcal {S}}' &{} = &{} ({\mathcal {L}}', F', {\mathcal {R}}', on', f_0'), &{} \quad \text{ with } {\mathcal {L}}' = \langle L_1',\ldots ,L_n'\rangle , \end{array} \end{aligned}$$

and consider the problem of showing that ${\mathcal {S}}$ is recursively $\pi$-mappable to ${\mathcal {S}}'$.

We construct the component bijection $\alpha _\pi$ as in Sect. 6.1. Then, following Definition 73, we check that either (a) $L_i$ and $L'_{\alpha _\pi (i)}$ are both leaf GLTSs, or (b) both are nested supercombinators; in the latter case, we then check (recursively) that $L_i$ is recursively $\pi$-mappable to $L'_{\alpha _\pi (i)}$.

We now consider format $\pi$-bisimulations. We can calculate the maximal format $\pi$-bisimulation between ${\mathcal {S}}$ and ${\mathcal {S}}'$ using a straightforward adaptation of the algorithm for calculating a strong bisimulation. Given a relation $\mathord {\sim ^F} \subseteq F \times F'$ over formats, define ${\mathcal {F}}(\sim ^F)$ to contain all pairs $(f, f')$ satisfying the defining conditions for a format $\pi$-bisimulation, i.e.

• if $(e,a,r,f_1) \in {\mathcal {R}}(f)$ then there is a rule $(e',\pi (a), \alpha (r),f_1') \in {\mathcal {R}}'(f')$ such that $\forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i))$ and $f_1 \sim ^F f_1'$;

• if $(e',a,r,f_1') \in {\mathcal {R}}'(f')$ then there is a rule $(e,\pi ^{-1}(a), \alpha ^{-1}(r),f_1) \in {\mathcal {R}}(f)$ such that $\forall i \in \{1,\ldots ,n\} \cdot e'(\alpha (i)) = \pi (e(i))$ and $f_1 \sim ^F f_1'$;

• $\alpha (on(f)) = on'(f')$.

Then we calculate the greatest fixed point of ${\mathcal {F}}$: let $\mathord {\sim _{\pi ,0}^F} = F \times F'$ be the universal relation over formats; calculate ${\mathcal {F}}(\sim _{\pi ,0}^F), {\mathcal {F}}^2(\sim _{\pi ,0}^F), \ldots$, until a fixed point $\sim ^F_\pi$ is reached. We then check that the initial formats are related, i.e. $f_0 \sim ^F_\pi f_0'$. If this succeeds, then ${\mathcal {S}}$ and ${\mathcal {S}}'$ are recursively $\pi$-mappable. (We store the format bisimulation found, for later use.)

Recall, that we apply the above procedure to show that the supercombinator for the implementation, ${\mathcal {S}}_{impl}$, is recursively $\pi$-mappable to itself, for every $\pi$ in a set of generators of the full symmetry group. By Lemma 77, this tells us that ${\mathcal {S}}_{impl}$ is recursively $\pi$-mappable to itself for every event permutation $\pi$. This means that for each event permutation $\pi$ there is a bijection $\alpha _\pi$ on the components of ${\mathcal {S}}_{impl}$ giving corresponding components. Inductively, for every event permutation $\pi$, and for every nested supercombinator ${\mathcal {S}}$ (nested at an arbitrary depth), there is a nested supercombinator ${\mathcal {S}}'$ such that ${\mathcal {S}}$ is recursively $\pi$-mappable to ${\mathcal {S}}'$. If $\pi$ can be written in terms of generators as $\pi = \pi _1;\ldots ;\pi _n$ then there are supercombinators ${\mathcal {S}}_0 = {\mathcal {S}}, {\mathcal {S}}_1, \ldots , {{\mathcal {S}}_n = {\mathcal {S}}'}$ such that for each i,  ${\mathcal {S}}_{i-1}$ is recursively $\pi _i$-mappable to ${\mathcal {S}}_i$ using some component bijection $\alpha _{\pi _i}^{{\mathcal {S}}_{i-1},{\mathcal {S}}_i}$ and format bisimulation $\sim _\pi ^{F,{\mathcal {S}}_{i-1},{\mathcal {S}}_i}$. Then, by Lemma 76, the component bijection and format bisimulation between the components of ${\mathcal {S}}$ and ${\mathcal {S}}'$ are

$$\begin{aligned} \begin{aligned} \alpha _\pi ^{{\mathcal {S}},{\mathcal {S}}'}&= \alpha _{\pi _1}^{{\mathcal {S}}_0,{\mathcal {S}}_1} ; \ldots ; \alpha _{\pi _n}^{{\mathcal {S}}_{n-1},{\mathcal {S}}_n}, \\ \sim _\pi ^{F,{\mathcal {S}},{\mathcal {S}}'}&= \sim _{\pi _1}^{F,{\mathcal {S}}_0,{\mathcal {S}}_1} ; \ldots ; \sim _{\pi _n}^{F,{\mathcal {S}}_{n-1},{\mathcal {S}}_n} . \end{aligned} \end{aligned}$$

1.2 D.2 Applying permutations to states

Suppose ${\mathcal {S}}$ is recursively $\pi$-mappable to ${\mathcal {S}}'$. We explain how to apply permutation $\pi$ to a state of ${\mathcal {S}}$ to produce a state of ${\mathcal {S}}'$. The lemma below shows how, given leaf components L and $L'$ such that $L' = \pi (L)$, to apply $\pi$ to a state of L to obtain a state of $L'$.

Lemma 78

Suppose L and $L'$ are leaf components with $L' = \pi (L)$. Then for each state s of L, there is a state $s'$ of $L'$ such that $s \sim _\pi s'$. We write $\pi (s)$ for this state $s'$.

Proof

If L and $L'$ are uncompressed leaf components, then, as for Lemma 34, if s has label $(Q,\rho )$, then we take $s'$ to be the state with label $(Q,\pi \mathbin {\scriptstyle \circ }\rho )$. If L and $L'$ are compressed leaf components, then the state $s''$ with label $(Q,\pi \mathbin {\scriptstyle \circ }\rho )$ might not exist in $L'$, because the compression has merged it with another state $s'$. However, $s'$ will be strongly bisimilar to $s''$, and so satisfy the conditions of the lemma. $\square$

The following proposition shows how, given a state $\sigma$ of a supercombinator and a permutation $\pi$, to calculate a state, which we denote $\pi (\sigma )$, such that $\sigma \sim _\pi \pi (\sigma )$.

Proposition 79

Let ${\mathcal {S}}$ and ${\mathcal {S}}'$ be supercombinators with components $\langle L_1,\ldots ,L_n\rangle$ and $\langle L_1',\ldots ,L_n'\rangle$, and let $\pi$ be an event permutation. Suppose ${\mathcal {S}}$ is recursively $\pi$-mappable to ${\mathcal {S}}'$ using component bijection $\alpha$ and format $\pi$-bisimulation $\sim ^F_\pi$. Consider the state

$$\begin{aligned} \sigma = ( s_1, \ldots , s_n, f). \end{aligned}$$

Define $\pi (\sigma )$ to be the state $( s_1', \ldots , s_n', f' )$, where

• if $L_i'$ is a leaf component, then $s'_i = \pi (s_{\alpha ^{-1}(i)})$, constructed as described in Lemma 78;

• if $L_i'$ is a nested supercombinator, then $s_i' = \pi (s_{\alpha ^{-1}(i)})$, defined recursively;

• $f \sim _\pi ^F f'$.

Then $\sigma \sim _\pi \pi (\sigma )$.

Proof

The proof is by induction on the depth of the tree of nested supercombinators. If $L_i'$ is a leaf GLTS, then so is $L_{\alpha ^{-1}(i)}$, and $L_{\alpha ^{-1}(i)} \sim _\pi L_i'$, by the definition of recursive $\pi$-mappable; then the existence of $s'_i$ follows from Lemma 78 and $s_{\alpha ^{-1}(i)} \sim _\pi s_i'$. If $L_i'$ is a nested supercombinator, then so is $L_{\alpha ^{-1}(i)}$, and $L_{\alpha ^{-1}(i)}$ is recursively $\pi$-mappable to $L_i'$; then by the inductive hypothesis, $L_i'$ has a state $s_i' = \pi (s_{\alpha ^{-1}(i)})$ such that $s_{\alpha ^{-1}(i)} \sim _\pi s_i'$. In each case, $s_j \sim _\pi s'_{\alpha (j)}$, for each j. Hence $\sigma \sim _\pi \pi (\sigma )$ by Lemma 71. $\square$