Abstract
Graphs are ubiquitous in computer science. Moreover, in various application fields, graphs are equipped with attributes to express additional information such as names of entities or weights of relationships. Due to the pervasiveness of attributed graphs, it is highly important to have the means to express properties on attributed graphs to strengthen modeling capabilities and to enable analysis. Firstly, we introduce a new logic of attributed graph properties, where the graph part and attribution part are neatly separated. The graph part is equivalent to first-order logic on graphs as introduced by Courcelle. It employs graph morphisms to allow the specification of complex graph patterns. The attribution part is added to this graph part by reverting to the symbolic approach to graph attribution, where attributes are represented symbolically by variables whose possible values are specified by a set of constraints making use of algebraic specifications. Secondly, we extend our refutationally complete tableau-based reasoning method as well as our symbolic model generation approach for graph properties to attributed graph properties. Due to the new logic mentioned above, neatly separating the graph and attribution parts, and the categorical constructions employed only on a more abstract level, we can leave the graph part of the algorithms seemingly unchanged. For the integration of the attribution part into the algorithms, we use an oracle, allowing for flexible adoption of different available SMT solvers in the actual implementation. Finally, our automated reasoning approach for attributed graph properties is implemented in the tool AutoGraph integrating in particular the SMT solver Z3 for the attribute part of the properties. We motivate and illustrate our work with a particular application scenario on graph database query validation.
















Similar content being viewed by others
Notes
Firstly, the algebraic specification used is given by \((\Sigma _{A_2}, EQ )\) where \(\Sigma _{A_2}\) is the signature with variables obtained for the attribution \(A_2\) of \(G_2^{ sa }\) and the signature \(\Sigma \) from \( SP \) as in Definition 10. Secondly, \(f_{AX}: AX _1\rightarrow AX _2\) is a member of \(\mathcal {V}_{\Sigma _{A_1},\Sigma _{A_2}} \) according to Definition 4.
The empty conjunction \(\wedge \emptyset \) is the base case of the inductive definition.
Formally, the family is a map that assigns one triple to each \(i\in I'\).
Intuitively, a triple \(\langle T_i,j,c_i\rangle \) is either generated by the initialization rule or is generated by the nesting rule and \(T_i\) is a tableau for a condition \(c_i\) that is the inner condition of some literal \(\ell =\exists (m,c_i)\) that is in a leaf node of the parent tableau \(T_j\) that is assigned to index j in \( NT \).
References
Abiteboul, S., Hull, R., Vianu, V. (eds.): Foundations of Databases: The Logical Level, 1st edn. Addison-Wesley Longman Publishing Co., Inc., Boston, MA (1995)
Angles, R., Arenas, M., Barceló, P., Hogan, A., Reutter, J.L., Vrgoc, D.: Foundations of modern graph query languages. CoRR, abs/1610.06264 (2016)
Angles, R., Gutierrez, C.: Survey of graph database models. ACM Comput. Surv. 40(1), 1:1–1:39 (2008)
Bak, K., Diskin, Z., Antkiewicz, M., Czarnecki, K., Wasowski, A.: Clafer: unifying class and feature modeling. Softw. Syst. Model. 15(3), 811–845 (2016)
Baudry, B.: Testing model transformations: a case for test generation from input domain models. In: Model-Driven Engineering for Distributed Real-Time Systems, Chap. 3, pp. 43–72. Wiley (2013). https://doi.org/10.1002/9781118558096.ch3
Beyhl, T., Blouin, D., Giese, H., Lambers, L.: On the operationalization of graph queries with generalized discrimination networks. In: Echahed and Minas [12], pp. 170–186
Blanco, R., Tuya, J.: A test model for graph database applications: an MDA-based approach. In: Vos Tanja E.J. Eldh, S., Prasetya, W. (eds.) Proceedings of the 6th International Workshop on Automating Test Case Design, Selection and Evaluation, A-TEST 2015, Bergamo, Italy, August 30–31, 2015, pp. 8–15. ACM (2015)
Codd, E.F.: A relational model of data for large shared data banks. Commun. ACM 13(6), 377–387 (1970)
Courcelle, B.: The expression of graph properties and graph transformations in monadic second-order logic. In: Rozenberg [44], pp. 313–400
Daniel, G., Sunyé, G., Cabot, J.: Umltographdb: mapping conceptual schemas to graph databases. In: Comyn-Wattiau, I., Tanaka, K., Song, I.-Y., Yamamoto, S., Saeki, M. (eds.) Conceptual Modeling—35th International Conference, volume 9974 of Lecture Notes in Computer Science, pp. 430–444 (2016)
Deckwerth, F.: Static verification techniques for attributed graph transformations. Ph.D. thesis, Darmstadt University of Technology, Germany (2017)
Echahed, R., Minas, M. (eds.): Graph Transformation—9th International Conference, ICGT 2016, in Memory of Hartmut Ehrig, Held as Part of STAF 2016, Vienna, Austria, July 5–6, 2016, Proceedings, volume 9761 of Lecture Notes in Computer Science. Springer (2016)
Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Fundamentals of Algebraic Graph Transformation. Springer, Berlin (2006)
Ehrig, H., Golas, U., Habel, A., Lambers, L., Orejas, F.: \(\cal{M}\)-adhesive transformation systems with nested application conditions. Part 2: embedding, critical pairs and local confluence. Fundam. Inform. 118(1–2), 35–63 (2012). https://doi.org/10.3233/FI-2012-705
Ehrig, H., Heckel, R., Rozenberg, G., Taentzer, G., (eds.): Graph Transformations, 4th International Conference, ICGT 2008, Leicester, United Kingdom, September 7–13, 2008. Proceedings, volume 5214 of Lecture Notes in Computer Science. Springer (2008)
Ehrig, H., Mahr, B.: Fundamentals of algebraic specification 1: equations und initial semantics. In: EATCS Monographs on Theoretical Computer Science, vol. 6. Springer, Heidelberg (1985). https://doi.org/10.1007/978-3-642-69962-7
Giese, H., König, B. (eds.): Graph Transformation—7th International Conference, ICGT 2014, Held as Part of STAF 2014, York, UK, July 22–24, 2014. Proceedings, volume 8571 of Lecture Notes in Computer Science. Springer (2014)
Gogolla, M., Hilken, F.: Model validation and verification options in a contemporary UML and OCL analysis tool. In: Oberweis, A., Reussner, R.H., (eds.) Modellierung 2016, 2.-4. März 2016, Karlsruhe, volume 254 of LNI, pp. 205–220. GI (2016)
González, C.A., Cabot, J.: Test data generation for model transformations combining partition and constraint analysis. In: Ruscio, D.D., Varró, D. (eds.) Theory and Practice of Model Transformations—7th International Conference, ICMT 2014, Held as Part of STAF 2014, York, UK, July 21–22, 2014. Proceedings, volume 8568 of Lecture Notes in Computer Science, pp. 25–41. Springer (2014)
Habel, A., Heckel, R., Taentzer, G.: Graph grammars with negative application conditions. Fundam. Inform. 26(3/4), 287–313 (1996)
Habel, A., Pennemann, K.-H.: Correctness of high-level transformation systems relative to nested conditions. Math. Struct. Comput. Sci. 19(2), 245–296 (2009)
Hähnle, R.: Tableaux and related methods. In Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning (in 2 volumes), pp. 100–178. Elsevier and MIT Press (2001)
Heckel, R., Wagner, A.: Ensuring consistency of conditional graph rewriting—a constructive approach. Electr. Notes Theor. Comput. Sci. 2, 118–126 (1995)
Jackson, E.K., Levendovszky, T., Balasubramanian, D.: Reasoning about metamodeling with formal specifications and automatic proofs. In: Whittle, J., Clark, T., Kühne, T. (eds.) Model Driven Engineering Languages and Systems, 14th International Conference, MODELS 2011, Wellington, New Zealand, October 16–21, 2011. Proceedings, volume 6981 of Lecture Notes in Computer Science, pp. 653–667. Springer (2011)
Jackson, E.K., Sztipanovits, J.: Constructive techniques for meta- and model-level reasoning. In: Engels, G., Opdyke, B., Schmidt, D.C., Weil, F. (eds.) Model Driven Engineering Languages and Systems, 10th International Conference, MoDELS 2007, Nashville, USA, September 30–October 5, 2007, Proceedings, volume 4735 of Lecture Notes in Computer Science, pp. 405–419. Springer (2007)
Krause, C., Johannsen, D., Deeb, R., Sattler, K.-U., Knacker, D., Niadzelka, A.: An SQL-based query language and engine for graph pattern matching. In: Echahed and Minas [12], pp. 153–169
Lambers, L., Orejas, F.: Tableau-based reasoning for graph properties. In: Giese and König [17], pp. 17–32
Microsoft Corporation. Z3. https://github.com/Z3Prover/z3. Accessed 19 Sept 2017
Milicevic, A., Near, J.P., Eunsuk, K., Jackson, D.: Alloy*: a general-purpose higher-order relational constraint solver. In: Bertolino, A., Canfora, G., Elbaum, S.G. (eds.) 37th IEEE/ACM International Conference on Software Engineering, ICSE 2015, Florence, Italy, May 16–24, 2015, Volume 1, pp. 609–619. IEEE Computer Society (2015)
Mougenot, A., Darrasse, A., Blanc, X., Soria, M.: Uniform random generation of huge metamodel instances. In: Paige, R.F., Hartman, A., Rensink, A. (eds.) Model Driven Architecture—Foundations and Applications, 5th European Conference, ECMDA-FA 2009, Enschede, The Netherlands, June 23–26, 2009. Proceedings, volume 5562 of Lecture Notes in Computer Science, pp. 130–145. Springer (2009)
Nelson, T., Saghafi, S., Dougherty, D.J., Fisler, K., Krishnamurthi, S.: Aluminum: principled scenario exploration through minimality. In: Notkin, D., Cheng, B.H.C., Pohl, K. (eds.) 35th International Conference on Software Engineering, ICSE ’13, San Francisco, CA, USA, May 18–26, 2013, pp. 232–241. IEEE Computer Society (2013)
Orejas, F.: Attributed graph constraints. In: Ehrig et al. [15], pp. 274–288
Orejas, F., Ehrig, H., Prange, U.: A logic of graph constraints. In: Fiadeiro, J.L., Inverardi, P. (eds.) Fundamental Approaches to Software Engineering, 11th International Conference, FASE 2008, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2008, Budapest, Hungary, March 29-April 6, 2008. Proceedings, volume 4961 of Lecture Notes in Computer Science, pp. 179–198. Springer (2008)
Orejas, F., Ehrig, H., Prange, U.: Reasoning with graph constraints. Formal Asp. Comput. 22(3–4), 385–422 (2010)
Orejas, F., Lambers, L.: Symbolic attributed graphs for attributed graph transformation. ECEASST 30, (2010). https://doi.org/10.1016/j.jsc.2010.09.009
Orejas, F., Lambers, L.: Lazy graph transformation. Fundam. Inform. 118(1–2), 65–96 (2012)
Pennemann, K.-H.: An algorithm for approximating the satisfiability problem of high-level conditions. Electr. Notes Theor. Comput. Sci. 213(1), 75–94 (2008)
Pennemann, K.-H.: Resolution-like theorem proving for high-level conditions. In: Ehrig et al. [15], pp. 289–304
Pennemann, K.-H.: Development of correct graph transformation systems, Ph.D. Thesis. Dept. Informatik, Univ. Oldenburg (2009)
Poskitt, C.M., Plump, D.: Verifying monadic second-order properties of graph programs. In: Giese and König [17], pp. 33–48
Radke, H.: HR* graph conditions between counting monadic second-order and second-order graph formulas. ECEASST 61, (2013). https://doi.org/10.14279/tuj.eceasst.61.831.831
Radke, H., Arendt, T., Becker, J.S., Habel, A., Taentzer, G.: Translating essential OCL invariants to nested graph constraints focusing on set operations. In: Parisi-Presicce, F., Westfechtel, B. (eds.) Graph Transformation—8th International Conference, ICGT 2015, Held as Part of STAF 2015, L’Aquila, Italy, July 21–23, 2015. Proceedings, volume 9151 of Lecture Notes in Computer Science, pp. 155–170. Springer (2015)
Rensink, A.: Representing first-order logic using graphs. In: Ehrig, H., Engels, G., Parisi-Presicce, F., Rozenberg, G. (eds.) Graph Transformations, Second International Conference, ICGT 2004, Rome, Italy, September 28–October 2, 2004, Proceedings, volume 3256 of Lecture Notes in Computer Science, pp. 319–335. Springer (2004)
Rozenberg, G. (ed.).: Handbook of graph grammars and computing by graph transformations, vol. 1: foundations. World Scientific (1997). https://doi.org/10.1142/3303
Salay, R., Chechik, M.: A generalized formal framework for partial modeling. In: Egyed, A., Schaefer, I. (eds.) Fundamental Approaches to Software Engineering—18th International Conference, FASE 2015, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2015, London, UK, April 11–18, 2015. Proceedings, volume 9033 of Lecture Notes in Computer Science, pp. 133–148. Springer (2015)
Schneider, S., Lambers, L., Orejas, F.: Symbolic model generation for graph properties. In: Huisman, M., Rubin, J. (eds). Fundamental Approaches to Software Engineering—20th International Conference, FASE 2017, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2017, Uppsala, Sweden, April 22–29, 2017, Proceedings, volume 10202 of Lecture Notes in Computer Science, pp. 226–243. Springer (2017)
Schneider, S., Lambers, L., Orejas, F.: Symbolic model generation for graph properties (extended version). Number 115 in Technische Berichte des Hasso-Plattner-Instituts fr Softwaresystemtechnik an der Universität Potsdam. Universitätsverlag Potsdam, Hasso Plattner Institute (Germany, Potsdam), 1 edition, 2 (2017)
Schweikardt, N., Schwentick, T., Segoufin, L.: Algorithms and Theory of Computation Handbook. Chapter Database Theory: Query Languages, vol. 19, pp. 1–34. Chapman & Hall/CRC, Boca Raton (2010)
Semeráth, O., Varró, D.: Graph constraint evaluation over partial models by constraint rewriting. In: Guerra, E., van den Brand, M. (eds.) Theory and Practice of Model Transformation—10th International Conference, ICMT 2017, Held as Part of STAF 2017, Marburg, Germany, July 17–18, 2017, Proceedings, volume 10374 of Lecture Notes in Computer Science, pp. 138–154. Springer (2017)
Semeráth, O., Vörös, A., Varró, D.: Iterative and incremental model generation by logic solvers. In: Stevens, P., Wasowski, A. (eds.) Fundamental Approaches to Software Engineering—19th International Conference, FASE 2016, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2016, Eindhoven, The Netherlands, April 2–8, 2016, Proceedings, volume 9633 of Lecture Notes in Computer Science, pp. 87–103. Springer (2016)
The Linked Data Benchmark Council (LDBC). Social network benchmark. https://github.com/ldbc/ldbc_snb_docs. Accessed: 21 Aug 2017
The World Wide Web Consortium (W3C). W3c xml schema definition language (xsd) 1.1 part 1: Structures (2012)
Wood, P.T.: Query languages for graph databases. SIGMOD Rec. 41(1), 50–60 (2012)
Author information
Authors and Affiliations
Corresponding author
Appendices
Some details on AutoGraph
Definition 30
(Z3 Signature)
Furthermore, we assume sufficient operations for constructing values of \(\mathsf {string}\) as terms such as \(\mathsf {a},\dots ,\mathsf {z},\mathsf {0},\dots ,\mathsf {9},\mathsf {-},\mathsf {SPACE}:{}\rightarrow \mathsf {string} \).
Categorical preliminaries and properties of GraphsSTA
Lemma 11
(GraphsSTA: Characterization of the Monomorphisms, Epimorphisms, and Isomorphisms) A graph morphism \(f:G\rightarrow G'\) from the category GraphsSTA is a mono(morphism) (epi(morphism)) (iso(morphism)), if each of its components is injective (surjective) (bijective), respectively. And, for isomorphisms, we additionally require that the reversed implication from Definition 11 holds as well, i.e., for all \(\sigma \in \mathcal {V}_{\Sigma _{A_2},\Sigma _{A_2}} \): \(\sigma \models f_{ AX }(\varPhi _1)\) implies \(\sigma \models \varPhi _2\).
Proof
(idea) Due to the componentwise characterization.
Definition 31
(\(\mathcal {E}\)-\(\mathcal {M}\)-Factorization) Given a category, a set \(\mathcal {E}\) of epimorphisms, and a set \(\mathcal {M}\) of monomorphisms. The category has \(\mathcal {E}\)-\(\mathcal {M}\) -Factorizations, if
-
(existence) for each \(f:A\rightarrow C\) there are \((e:A\twoheadrightarrow K)\in \mathcal {E}\) and
 s.t. \(m\circ e=f\) and
s.t. \(m\circ e=f\) and -
(uniqueness) for \((e':A\twoheadrightarrow K')\in \mathcal {E}\) and
 with \(m'\circ e'=f\) there is
with \(m'\circ e'=f\) there is  with \(i\circ e=e'\) and \(m'\circ i=m\).
with \(i\circ e=e'\) and \(m'\circ i=m\).
Definition 32
(Jointly Epimorphic Morphisms [13, Definition A.16, p. 334]) Two morphisms \(e_1:A_1\rightarrow B\) and \(e_2:A_2\rightarrow B\) of a category are Jointly Epimorphic, if any two morphisms \(g,h:B\rightarrow C\) are equal whenever \(g\circ e_i=h\circ e_i\) (for each \(1\le i \le 2\)).
Pair Factorization (cf. [13, Definition 5.25, p. 122]) has the intuition that any two morphisms \(f_1\) and \(f_2\) with common codomain C coincide (in the sense of mapping to the same elements) on a well-defined subgraph K of C. That K does not include further elements (on which the two morphisms do not coincide) is expressed by stating that the morphisms \(e_1\) and \(e_2\) are jointly epimorphic and the coincidence is expressed by stating that m is a monomorphism together with the commutation.
Definition 33
(\(\mathcal {E'}\)-\(\mathcal {M}\)-Pair Factorization) For a given category, a set \(\mathcal {E'}\) of pairs \((f_1,f_2)\) of jointly epi morphisms, and a set \(\mathcal {M}\) of monomorphisms. The category has \(\mathcal {E'}\)-\(\mathcal {M}\)
-Pair Factorizations, if for each two morphisms \(f_1:A_1\rightarrow C\) and \(f_2:A_2\rightarrow C\) there are \((e_1:A_1\rightarrow K,e_2:A_2\rightarrow K)\in \mathcal {E'}\) and  s.t. \(m\circ e_i=f_i\) (for each \(1\le i\le 2\)).
s.t. \(m\circ e_i=f_i\) (for each \(1\le i\le 2\)).
Definition 34
(Binary Coproduct) A category has binary coproducts, if for every \(A_i\) (with \(1\le i\le 2\)) there are \(f_i:A_i\rightarrow C\) (for each \(1\le i\le 2\)) s.t. (the following universal property holds) for all \(g_i:A_i\rightarrow X\) there is a unique \(h:C\rightarrow X\) with \(h\circ f_i=g_i\) (for each \(1\le i\le 2\)).
Lemma 12
(GraphsSTA has Binary Coproducts)
Proof
(idea) The binary coproduct C with morphisms \(f_1\) and \(f_2\) from Definition 34 is constructed componentwise using the disjoint union, as usual.
For the category GraphsSTA, we use as \(\mathcal {E}\) the set of all epimorphisms, as \(\mathcal {M}\) the set of all monomorphisms, and as \(\mathcal {E'}\) the set of all pairs of jointly epimorphic morphisms.
Lemma 13
(GraphsSTA has \(\mathcal {E}\)-\(\mathcal {M}\)-Factorization)
Proof
(idea) The morphisms e and m, required according to Definition 31, are constructed componentwise for a morphism f.
Lemma 14
(GraphsSTA has \(\mathcal {E'}\)-\(\mathcal {M}\)-Pair Factorization)
Proof
(idea) Analogously to [13, Remark 5.26, p. 122], we construct the \(\mathcal {E'}\)-\(\mathcal {M}\)-Pair Factorizations using \(\mathcal {E}\)-\(\mathcal {M}\)-Factorizations (based on Lemma 13) and binary coproducts (based on Lemma 12).
Proofs
Proof of Lemma 2
Part1 (\(\subseteq \)).
for some q:C G
G
for some \(c\in S\)
Part2 (\(\supseteq \)).
for some \(c\in S\)
for some 
Proof of Lemma 5
Part1 (\(\subseteq \)).

for some 

for some 
Part2 (\(\supseteq \)).
for some 

Proof of Lemma 6
Part1 (C is an element).
for 
for each \(1\le i\le n\) simultaneously
there is no  such that \(q_i\models c_i\) and \(q_i\circ m_i=q\)
such that \(q_i\models c_i\) and \(q_i\circ m_i=q\)
Part2 (unique least element).
for some 
Proof of Lemma 3
Part1 (\(\subseteq \)).

for some 

for some 
also
Part2 (\(\supseteq \)).
for some 
for some 
also

Proof of Lemma 8
Part1.1 (if).
because \( covered (\mathcal {S}-\mathcal {S} ') \subseteq covered (\mathcal {S}) \)
Part1.2 (only if).
because \( covered (\mathcal {S})- covered (\mathcal {S} ') \subseteq covered (\mathcal {S}-\mathcal {S} ') \)
because \(\mathcal {S} '\subseteq \mathcal {S} \) implies \( covered (\mathcal {S} ') \subseteq covered (\mathcal {S}) \)
Part2.
Proof of Lemma 9
-
Part1 (if). Fix some \(\langle C,\wedge \emptyset \rangle \in \mathcal {S} \).
Assume for the contradiction \( covered (\mathcal {S}) = covered (\mathcal {S}-\{\langle C,\wedge \emptyset \rangle \}) \). Hence, for each \(G\in covered (\langle C,\wedge \emptyset \rangle ) \) there is some other \(\langle C',\wedge \emptyset \rangle \in \mathcal {S} \) s.t. \(G\in covered (\langle C,\wedge \emptyset \rangle ) \).
Note that \(C\in covered (\langle C',\wedge \emptyset \rangle ) \). Hence, we are able to pick some \(\langle C',\wedge \emptyset \rangle \) s.t. \(C\in covered (\langle C',\wedge \emptyset \rangle ) \).
Hence, there is a monomorphism
 .
.This is a contradiction.
-
Part2 (only if). Fix distinct \(\langle C,\wedge \emptyset \rangle \in \mathcal {S} \) and \(\langle C',\wedge \emptyset \rangle \in \mathcal {S} \).
Assume for the contradiction that
 is a monomorphism.
is a monomorphism.Hence \( covered (\langle C,\wedge \emptyset \rangle ) \subseteq covered (\langle C',\wedge \emptyset \rangle ) \).
Hence \( covered (\mathcal {S}) = covered (\mathcal {S}-\{\langle C,\wedge \emptyset \rangle \}) \).
Hence \(\mathcal {S} \) is not compact.
This is a contradiction.
Proof of Corollary 1
-
Let \(\mathcal {S} \) be nonambiguous, (sound,) complete, minimally representable.
-
We show that \(\mathcal {S} \) is compact.
-
Fix some \(\langle C,c\rangle \in \mathcal {S} \).
-
We show that \( covered (\mathcal {S}) \ne covered (\mathcal {S}-\{\langle C,c\rangle \}) \).
-
We show that \(C\in covered (\mathcal {S}) \).
From minimally representability we have that \(C\models p\).
From completeness we that \(C\in covered (\mathcal {S}) \).
-
We show that \(C\notin covered (\mathcal {S}-\{\langle C,c\rangle ) \).
Assume for the contradiction that \(\langle C',c'\rangle \in \mathcal {S}-\{\langle C,c\rangle \) such that \(C\in covered (\langle C',c'\rangle ) \).
Then, \( covered (\langle C',c'\rangle ) \cap covered (\langle C,c\rangle ) \ne \emptyset \) contradicts nonambiguity because \(\langle C',c'\rangle \ne \langle C,c\rangle \).
-
Lemma 15
(Satisfaction is a Congruence) Let \(c_1\) and \(c_2\) be conditions from \(\mathcal {C}_{C} \) such that \(\{q\mid q\models c_1\}=\{q\mid q\models c_2\}\). Then all following items are satisfied.
-
\(\{q\mid q\models \wedge (S\cup \{c_1\})\} =\{q\mid q\models \wedge (S\cup \{c_2\})\}\) for all finite \(S\subseteq \mathcal {C}_{C} \).
-
\(\{q\mid q\models \lnot c_1\} =\{q\mid q\models \lnot c_2\}\).
-
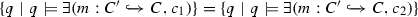 for every
for every  .
.
Proof of Lemma 15
Fix \(c_1,c_2\in \mathcal {C}_{C} \).
Assume (A) that \(\{q\mid q\models c_1\}=\{q\mid q\models c_2\}\). In each case, we show only one direction wlog.
-
Fix some \(S\subseteq \mathcal {C}_{C} \) that is finite.
Fix some
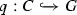 such that \(q\models \wedge (S\cup \{c_1\})\).
such that \(q\models \wedge (S\cup \{c_1\})\).Hence, \(q\models \wedge S\) and \(q\models c_1\).
From (A) we have that \(q\models c_2\).
Hence, \(q\models \wedge (S\cup \{c_2\})\).
-
Fix some
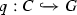 such that \(q\models \lnot c_1\).
such that \(q\models \lnot c_1\).Hence, not \(q\models c_1\).
From (A) we have that not \(q\models c_2\).
Hence, \(q\models \lnot c_2\).
-
Fix some
 .
.Fix some
 such that
such that  .
.Hence, there is some
 such that \(q\models c_1\) and \(q\circ m=q'\).
such that \(q\models c_1\) and \(q\circ m=q'\).From (A) we have that \(q\models c_2\).
Hence,
 .
.
Proof of Lemma 4
The construction steps of \([\cdot ]\) replace subterms.
By structural induction relying on Lemma 15, it is sufficient to consider how one condition \(c_1\) is replaced by another condition \(c_2\) over same graph in the sense of \(\{q\mid q\models c_1\}=\{q\mid q\models c_2\}\).
We verify for all five steps of the operation \([\cdot ]\) that the property is rephrased equivalently.
-
Step 1: The unfolding of abbreviations is sound by default.
-
Step 2: We assume that
 has been replaced by \(c_2\).
has been replaced by \(c_2\).We perform an induction on \(c_1\).
-
Case: \(c_1=\lnot c_1'\) and, hence,
 for some \(c_2'\)
for some \(c_2'\)
As induction hypothesis, we assume that \(\{q\mid q\models c_1'\}=\{q\mid q\models c_2'\}\). We have to show
 , which is the direct consequence from Lemma 15.
, which is the direct consequence from Lemma 15. -
Case: \(c_1{=}\wedge \{c_{0,1},\dots ,c_{n,1}\}\) and, hence, \(c_2{=}\wedge \{c_{0,2},\dots ,c_{n,2}\}\) for some \(c_{0,2}\), ..., \(c_{n,2}\) As induction hypothesis we assume that \(\{q\mid q\models c_{i,1}\}=\{q\mid q\models c_{i,2}\}\) (for \(0\le i\le n\)) We have to show
 , which is the direct consequence from Lemma 15.
, which is the direct consequence from Lemma 15. -
Case:
 and, hence, \(c_2=\exists (m\circ i,c_1')\)
and, hence, \(c_2=\exists (m\circ i,c_1')\)
We have to show
 , which holds directly application of Definition 16.
, which holds directly application of Definition 16.
-
-
Step 3: We show that
 if
if 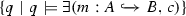 is empty. This is trivially the case because \(\{q\mid q\models \vee \emptyset \}\) is also empty.
is empty. This is trivially the case because \(\{q\mid q\models \vee \emptyset \}\) is also empty. -
Step 4: The mentioned replacement rules
\(\lnot (\wedge S){\mathop {=}\limits ^{\cdot }}\vee \{\lnot c\mid c\in S\}\),
\(\lnot (\vee S){\mathop {=}\limits ^{\cdot }}\wedge \{\lnot c\mid c\in S\}\), and
\(\lnot \lnot c{\mathop {=}\limits ^{\cdot }}c\)
are obviously sound in the sense of:
\(\{q\mid q\models lhs \}=\{q\mid q\models rhs \}\).
-
Step 5: The mentioned replacement rules
\(\wedge (S\cup \{\wedge S'\}){\mathop {=}\limits ^{\cdot }}\wedge (S\cup S')\),
\(\vee (S\cup \{\vee S'\}){\mathop {=}\limits ^{\cdot }}\vee (S\cup S')\),
\(\wedge (S\cup \{\vee S'\}){\mathop {=}\limits ^{\cdot }}\vee \{\wedge (S\cup \{c\})\mid c\in S'\}\), and
\(\vee (S\cup \{\wedge S'\}){\mathop {=}\limits ^{\cdot }}\wedge \{\vee (S\cup \{c\})\mid c\in S'\}\)
are obviously sound in the sense of:
\(\{q\mid q\models lhs \}=\{q\mid q\models rhs \}\).
Rights and permissions
About this article
Cite this article
Schneider, S., Lambers, L. & Orejas, F. Automated reasoning for attributed graph properties. Int J Softw Tools Technol Transfer 20, 705–737 (2018). https://doi.org/10.1007/s10009-018-0496-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10009-018-0496-3




 s.t.
s.t.  with
with  with
with  .
. is a monomorphism.
is a monomorphism.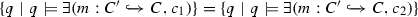 for every
for every  .
.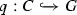 such that
such that 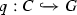 such that
such that  .
. such that
such that  .
. such that
such that  .
. has been replaced by
has been replaced by  for some
for some  , which is the direct consequence from Lemma
, which is the direct consequence from Lemma  , which is the direct consequence from Lemma
, which is the direct consequence from Lemma  and, hence,
and, hence,  , which holds directly application of Definition
, which holds directly application of Definition  if
if 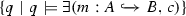 is empty. This is trivially the case because
is empty. This is trivially the case because