Skip to main content
SpringerLink
Log in

Effects of the nitrogen doping configuration and site on the thermal conductivity of defective armchair graphene nanoribbons

  • Original Paper
  • Published:
Journal of Molecular Modeling Aims and scope Submit manuscript

Abstract

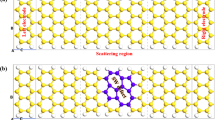
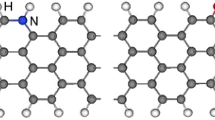
The influence of the nitrogen (N) doping configuration on the thermal conductivity (TC) of armchair graphene nanoribbons (AGNRs) of size 15.7 nm × 7.26 nm was investigated using classical molecular dynamics (MD) simulations with the optimized Tersoff potential at room temperature. The effect of changing the N-doping site in defects on the TC of AGNRs was also investigated in detail. The variations with N concentration of the TCs of AGNRs presenting graphitic N (quarternary N), pyridinic N, and pyrrolic N doping configurations were studied. Results of MD simulations showed that, among these three doping configurations, pyridinic N was associated with the highest TC, and pyrrolic N with the lowest TC. The highest TC values were obtained when the N dopant atoms were located at the edges and at defects in the AGNR. The presence of both pyrrolic N and Stone–Wales type 1 (SW-1) defects led to a higher TC than the presence of both pyrrolic N and SW-2 defects. Phonon–defect scattering was found to be influenced by changes in C–C bond orientation. SW-1 defects were found to exert a greater influence on the TC than graphitic N doping. Furthermore, the influence on the TC of the N-doping site location in SW-1 defects was examined. Doping the central sites of SW-1 defects was found to yield higher TC values than doping the edge sites of defects. Graphitic-N doping of the more central sites in a SW-1 defect led to a higher TC than the random graphitic-N doping of sites in a SW-1 defect.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, Grigorieva IV, Firsov AA (2004) Electric field effect in atomically thin carbon films. Science 306(5696):666–669

  2. Novoselov KS, Geim AK, Morozov SV, Jiang D, Katsnelson MI, Grigorieva IV, Dubonos SV, Firsov AA (2005) Two-dimensional gas of massless Dirac fermions in graphene. Nature 438:197–200

  3. Zhang YB, Tan YW, Stormer HL, Kim P (2005) Experimental observation of the quantum Hall effect and Berry's phase in graphene. Nature 438:201–204

  4. Geim AK, Novoselov KS (2007) The rise of graphene. Nat Mater 6(3):183–191

  5. Lee C, Wei X, Kysar JW, Hone J (2008) Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321(5887):385–388

  6. Balandin AA, Ghosh S, Bao W, Calizo I, Teweldebrhan D, Miao F, Lau CN (2008) Superior thermal conductivity of single-layer graphene. Nano Lett 8(3):902–907

  7. Williams JR, DiCarlo L, Marcus CM (2007) Quantum hall effect in a gate-controlled p-n junction of graphene. Science 317(5838):638–641

  8. Ghosh S, Calzio I, Teweldebrhan D, Pokatilov EP, Nika DL, Balandin AA, Bao W, Miao F, Lau CN (2008) Extremely high thermal conductivity of graphene: prospects for thermal management applications in nanoelectronic circuits. Appl Phys Lett 92(15):151911

  9. Cai WW, Moore AL, Zhu YW, Li XS, Chen SS, Shi L, Ruoff RS (2010) Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett 10(5):1645–1651

  10. Iwamoto Y, Yoshioka A, Naito T, Cuya J, Ido Y, Okawa R, Jeyadevan B, Yamaguchi H (2016) Field induced anisotropic thermal conductivity of silver nanowire dispersed-magnetic functional fluid. Exp Thermal Fluid Sci 79:111–117

  11. Faugeras C, Faugeras B, Orlita M, Potemski M, Nair RR, Geim AK (2010) Thermal conductivity of graphene in Corbino membrane geometry. ACS Nano 4(4):1889–1892

  12. Panchakarla LS, Subrahmanyam KS, Saha SK, Govindaraj A, Krishnamurthy HR, Waghmare UV, Rao CNR (2009) Synthesis, structure, and properties of boron- and nitrogen-doped graphene. Adv Mater 21(46):4726–4730

  13. Deng D, Pan X, Yu L, Cui Y, Jiang Y, Qi J, Li W-X, Fu Q, Ma X, Xue Q, Sun G, Bao X (2011) Toward N-doped graphene via solvothermal synthesis. Chem Mater 23(5):1188–1193

  14. Zhang C, Fu L, Liu N, Liu M, Wang Y, Liu Z (2011) Synthesis of nitrogen-doped graphene using embedded carbon and nitrogen sources. Adv Mater 23(8):1020–1024

  15. Wei D, Liu Y, Wang Y, Zhang H, Huang L, Yu G (2009) Synthesis of N-doped graphene by chemical vapor deposition and its electrical properties. Nano Lett 9(5):1752–1758

  16. Wang Y, Shao Y, Matson DW, Li J, Lin Y (2010) Nitrogen-doped graphene and its application in electrochemical biosensing. ACS Nano 4(4):1790–1798

  17. Wang X, Li X, Zhang L, Yoon Y, Weber PK, Wang H, Guo J, Dai H (2009) N-doping of graphene through electrothermal reactions with ammonia. Science 324(5928):768–771

  18. Ma FX, Wang J, Wang FB, Xia XH (2015) The room temperature electrochemical synthesis of N-doped graphene and its electrocatalytic activity for oxygen reduction. Chem Commun 51(7):1198–1201

  19. Wang R, Xu C, Sun J, Gao L (2014) Three-dimensional Fe2O3 nanocubes/nitrogen-doped graphene aerogels: nucleation mechanism and lithium storage properties. Sci Rep 4:7171

  20. Zhang Y, Ge J, Wang L, Wang D, Ding F, Tao X, Chen W (2013) Manageable N-doped graphene for high performance oxygen reduction reaction. Sci Rep 3:2771

  21. Wen ZH, Wang XC, Mao S, Bo Z, Kim H, Cui SM, Lu GH, Feng XL, Chen JH (2012) Crumpled nitrogen-doped graphene nanosheets with ultrahigh pore volume for high-performance supercapacitor. Adv Mater 24(41):5610–5616

  22. Lv R, Li Q, Botello-Méndez AR, Hayashi T, Wang B, Berkdemir A, Hao Q, Elías AL, Cruz-Silva R, Gutiérrez HR, Kim YA, Muramatsu H, Zhu J, Endo M, Terrones H, Charlier JC, Pan M, Terrones M (2012) Nitrogen-doped graphene: beyond single substitution and enhanced molecular sensing. Sci Rep 2:586

  23. Wang X, Tabakman SM, Dai H (2008) Atomic layer deposition of metal oxides on pristine and functionalized graphene. J Am Chem Soc 130(26):8152–8153

  24. Li X-F, Lian K, Liu L, Luo Y (2016) Unraveling the formation mechanism of graphitic nitrogen-doping in thermally treated graphene with ammonia. Sci Rep 6:23495

  25. Li X-J, Yu X-X, Liu J-Y, Fan X-D, Zhang K, Cai H-B, Pan N, Wang X-P (2012) Synthesis of nitrogen-doped graphene via thermal annealing graphene with urea. Chin J Chem Phys 25(3):325–329

  26. Lu YF, Lo S-T, Lin J-C, Zhang W, Lu J-Y, Liu F-H, Tseng C-M, Lee Y-H, Liang C-T, Li L-J (2013) Nitrogen-doped graphene sheets grown by chemical vapor deposition: synthesis and influence of nitrogen impurities on carrier transport. ACS Nano 7(8):6522–6532

  27. Wu J, Ma L, Yadav RM, Yang Y, Zhang X, Vajtai R, Lou J, Ajayan PM (2015) Nitrogen-doped graphene with pyridinic dominance as a highly active and stable electrocatalyst for oxygen reduction. ACS Appl Mater Interfaces 7(27):14763–14769

  28. Zheng B, Cai X-L, Zhou Y, Xia X-H (2016) Pure pyridinic nitrogen doped single-layer graphene catalyzes the two-electron transfer process of oxygen reduction reaction. ChemElectroChem 3(12):2036–2042

  29. Usachov D, Vilkov O, Grüneis A, Haberer D, Fedorov A, Adamchuk VK, Preobrajenski AB, Dudin P, Barinov A, Oehzelt M, Laubschat C, Vyalikh DV (2011) Nitrogen-doped graphene: efficient growth, structure, and electronic properties. Nano Lett 11(12):5401–5047

  30. Jalili S, Vaziri R (2011) Study of the electronic properties of Li-intercalated nitrogen doped graphite. Mol Phys 109(5):687–694

  31. Wang X, Sun G, Routh P, Kim D-H, Huang W, Chen P (2014) Heteroatom-doped graphene materials: syntheses, properties and applications. Chem Soc Rev 43(20):7067–7098

  32. Luo Z, Lim S, Tian Z, Shang J, Lai L, MacDonald B, Fu C, Shen Z, Yu T, Lin J (2011) Pyridinic N doped graphene: synthesis, electronic structure, and electrocatalytic property. J Mater Chem 21(22):8038–8044

  33. Lin Y-C, Teng P-Y, Yeh C-H, Koshino M, Chiu P-W, Suenaga K (2015) Structural and chemical dynamics of pyridinic-nitrogen defects in graphene. Nano Lett 15(11):7408–7413

  34. Mortazavi B, Rajabpour A, Ahzi S, Rémond Y, Allaei SMV (2012) Nitrogen doping and curvature effects on thermal conductivity of graphene: a non-equilibrium molecular dynamics study. Solid State Commun 152(4):261–264

  35. Yang H, Tang Y, Gong J, Liu Y, Wang X, Zhao Y, Yang P, Wang S (2013) Influence of doped nitrogen and vacancy defects on the thermal conductivity of graphene nanoribbons. J Mol Model 19(11):4781–4788

  36. Mortazavi B, Ahzi S (2012) Molecular dynamics study on the thermal conductivity and mechanical properties of boron doped graphene. Solid State Commun 152(15):1503–1507

  37. Setoodeh AR, Badjian H, Jahromi HS (2017) Atomistic study of mono/multi-atomic vacancy defects on the mechanical characterization of boron-doped graphene sheets. J Mol Model 23:2

  38. Mortazavi B, Ahzi S (2013) Thermal conductivity and tensile response of defective graphene: a molecular dynamics study. Carbon 63:460–470

  39. Yeo JJ, Liu Z, Ng TY (2012) Comparing the effects of dispersed Stone–Thrower–Wales defects and double vacancies on the thermal conductivity of graphene nanoribbons. Nanotechnology 23(38):385702

  40. Liu D, Yang P, Yuan X, Guo J, Liao N (2015) The defect location effect on thermal conductivity of graphene nanoribbons based on molecular dynamics. Phys Lett A 379(9):810–814

  41. Biel B, Blase X, Triozon F, Roche S (2009) Anomalous doping effects on charge transport in graphene nanoribbons. Phys Rev Lett 102:096803

  42. Biel B, Blase X, Triozon F, Roche S (2009) Chemically induced mobility gaps in graphene nanoribbons: a route for upscaling device performances. Nano Lett 9(7):2725–2729

  43. Zeng H, Zhao J, Wei JW, Hu HF (2011) Effect of N doping and Stone–Wales defects on the electronic properties of graphene nanoribbons. Eur Phys J B 79(3):335–340

  44. Accelrys Inc. (2017) Materials Studio. Accelrys Inc., San Francisco. https://accelrys.com

  45. Plimpton S (1995) Fast parallel algorithms for short-range molecular dynamics. J Comput Phys 117(1):1–19

  46. Tuckerman ME, Berne BJ, Martyna GJ (1992) Reversible multiple time scale molecular dynamics. J Chem Phys 97(3):1990–2001

  47. Lindsay L, Broido DA (2010) Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys Rev B 81(20):205441

  48. Tabarraei A, Shadalou S, Song J-H (2015) Mechanical properties of graphene nanoribbons with disordered edges. Comput Mater Sci 96:10–19

  49. Hoover WG (1985) Canonical dynamics: equilibrium phase-space distributions. Phys Rev A 31(3):1695–1697

  50. Bagri A, Kim SP, Ruoff RS, Shenoy VB (2011) Thermal transport across twin grain boundaries in polycrystalline graphene from nonequilibrium molecular dynamics simulations. Nano Lett 11(9):3917–3921

  51. Guo Z, Zhang D, Gong XG (2009) Thermal conductivity of graphene nanoribbons. Appl Phys Lett 95(16):163103

  52. Varshney V, Patnaik SS, Roy AK, Froudakis G, Farmer BL (2010) Modeling of thermal transport in pillared-graphene architectures. ACS Nano 4(2):1153–1161

  53. Wei Z, Ni Z, Bi K, Chen M, Chen Y (2011) In-plane lattice thermal conductivities of multilayer graphene films. Carbon 49(8):2653–2658

  54. Zhang G, Li B (2005) Thermal conductivity of nanotubes revisited: effects of chirality, isotope impurity, tube length, and temperature. J Chem Phys 123(11):114714

  55. Wang ZL, Tang DW, Zheng XH, Zhang WG, Zhu YT (2007) Length-dependent thermal conductivity of single-wall carbon nanotubes: prediction and measurements. Nanotechnology 18(47):475714

  56. Maruyama S (2002) A molecular dynamics simulation of heat conduction in finite length SWNTs. Physica B 323(1–4):193–195

  57. Jiang JW, Wang JS, Li B (2010) Topological effect on thermal conductivity in graphene. J Appl Phys 108(6):064307

  58. Ghosh S, Bao W, Nika DL, Subrina S, Pokatilov EP, Lau CN, Balandin AA (2010) Dimensional crossover of thermal transport in few-layer graphene. Nat Mater 9(7):555–558

  59. Klemens PG (2001) Theory of thermal conduction in thin ceramic films. Int J Thermophys 22(1):265–275

Download references

Acknowledgements

The authors greatly appreciate the valuable guidance provided by Dr. Bohayra Mortazavi at Bauhaus University. Our numerical calculations were partially executed at TUBITAK ULAKBIM, TRUBA.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Gebze Technical University, Gebze, 41400, Kocaeli, Turkey

    Ahmet Emin Senturk, Ahmet Sinan Oktem & Alp Er S. Konukman

Authors
  1. Ahmet Emin Senturk
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmet Sinan Oktem
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alp Er S. Konukman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alp Er S. Konukman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Senturk, A.E., Oktem, A.S. & Konukman, A.E.S. Effects of the nitrogen doping configuration and site on the thermal conductivity of defective armchair graphene nanoribbons. J Mol Model 23, 247 (2017). https://doi.org/10.1007/s00894-017-3415-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00894-017-3415-8

Keywords

Search

Navigation