Comparison and evaluation of state-of-the-art LSM merge policies

Abstract

Modern NoSQL database systems use log-structured merge (LSM) storage architectures to support high write throughput. LSM architectures aggregate writes in a mutable MemTable (stored in memory), which is regularly flushed to disk, creating a new immutable file called an SSTable. Some of the SSTables are chosen to be periodically merged—replaced with a single SSTable containing their union. A merge policy (a.k.a. compaction policy) specifies when to do merges and which SSTables to combine. A bounded depth merge policy is one that guarantees that the number of SSTables never exceeds a given parameter k, typically in the range 3–10. Bounded depth policies are useful in applications where low read latency is crucial, but they and their underlying combinatorics are not yet well understood. This paper compares several bounded depth policies, including representative policies from industrial NoSQL databases and two new ones based on recent theoretical modeling, as well as the standard Tiered policy and Leveled policy. The results validate the proposed theoretical model and show that, compared to the existing policies, the newly proposed policies can have substantially lower write amplification with comparable read amplification.

1 Introduction

Many modern NoSQL systems [8, 9] use log-structured merge (LSM) architectures [36] to achieve high write throughput. To insert a new record, a write operation simply inserts the record into the memory-resident MemTable [9] (also called the in-memory component). Update operations are implemented lazily, requiring only a single write to the MemTable. Delete operations are implemented similarly, by writing an anti-matter record for the key to the MemTable. Thus, each write, update, or delete operation avoids any immediate disk access. When the MemTable reaches its allocated capacity (or for other reasons), it is flushed to disk, creating an immutable disk file called a component, or, usually, an SSTable (Sorted Strings Table [9]). This process continues, creating many SSTables over time.

Each read operation searches the MemTable and SSTables to find the most recent value written for the given key. With a compact index stored in memory for each SSTable, checking whether a given SSTable contains a given key typically takes just one disk access [22, §2.5]. (For small SSTables, this access can sometimes be avoided by storing a Bloom filter for the SSTable in memory [14].) Hence, the time per read grows with the number of SSTables. To control read costs, the system periodically merges SSTables to reduce their number and to prune updated and anti-matter records. Each merge replaces some subset of the SSTables by a single new SSTable that holds their union. The merge batch-writes these items to the new SSTable on disk. The write amplification is the number of bytes written by all merges, divided by the number of bytes inserted by write operations.

A merge policy (also known as a compaction policy) determines how merges are done. The policy must efficiently trade off total write amplification for total read cost (which increases with the average number of SSTables being checked per read operation, known as read amplification). This paper focuses on what we call bounded depth policies—those that guarantee a bounded number of disk accesses for each read operation by ensuring that, at any given time, the SSTable count (the number of existing SSTables) never exceeds a given parameter k, typically 3–10, such that the read amplification is at most k. Maintaining bounded depth is important in applications that require low read latency, but bounded depth policies are not yet well understood.

A recent theoretical work by Mathieu et al. [35] (including one of the current authors) formally defines a broad class of so-called stack-based policies. (See Sect. 3 for the definition.) This class includes policies of many popular NoSQL systems, including Bigtable [9], HBase [19, 27, 37], Accumulo [26, 37], Cassandra [29], Hypertable [25], and AsterixDB [2]. In contrast, leveled policies (used by LevelDB and its spin-offs [21]) split SSTables by key space to avoid monolithic merges, so they do not fit the stack-based model. Note that all current leveled implementations yield unbounded depth; hence, they are not considered here.

Mathieu et al. [35] also propose theoretical metrics for policy evaluation and, as a proof of concept, propose new policies that, among stack-based policies, are optimal according to those metrics. Two such policies, MinLatency and Binomial (defined in Sect. 2) are bounded depth policies which were designed to have minimum worst-case write amplification (subject to the depth constraint) among all stack-based policies. Mathieu et al. [35] observe that, according to the theoretical model, on some inputs existing policies are far from optimal, so, on some common workloads, compared to existing policies, MinLatency and Binomial can have lower write amplification.

Here, we empirically compare MinLatency and Binomial to three representative bounded depth merge policies from state-of-the-art NoSQL databases: a policy from AsterixDB [6], Exploring (the default policy for HBase [5]), and the default policy from Bigtable (as described by Mathieu et al. [35], which includes authors from Google), as well as the standard Tiered policy (the default policy for Cassandra [4]) and Leveled policy (the default policy for LevelDB [21]). Section 2 defines these policies. We implement the policies under consideration on a common platform—Apache AsterixDB [2, 6]—and evaluate them on inputs from the Yahoo! Cloud Serving Benchmark (YCSB) [11, 44]. This is the first implementation and evaluation of the policies proposed by Mathieu et al. [35] on a real NoSQL system. The empirical results validate the theoretical model. MinLatency and Binomial achieve write amplification close to the theoretical minimum, thereby outperforming the other policies by orders of magnitude on some realistic workloads. (See Sect. 4.)

Having a realistic theoretical model facilitates merge policy design both via theoretical analysis (as for MinLatency and Binomial), and because it enables rapid but faithful simulation of experiments. NoSQL systems are designed to run for months, incorporating hundreds of terabytes. Experiments can take weeks, even with appropriate adaptations. In contrast, the model allows some experiments to be faithfully simulated in minutes. (See Sect. 5.)

In summary, this work makes the following contributions:

• 1. The implementation of several existing merge policies, including the popular Tiered and Leveled, and two recently proposed merge policies, on a common, open-source platform, specifically Apache AsterixDB.

• 2. An experimental evaluation on write, read, and transient space amplification using the Yahoo! Cloud Serving Benchmark (YCSB) benchmark, confirming that the recently proposed policies can significantly outperform the state-of-the-art policies on some common workloads, such as append-only and update-heavy workloads.

• 3. A study on how insertion order affects the write amplification of merge policies, especially for Leveled.

• 4. We have shown that Binomial and MinLatency outperform the popular Tiered and Leveled policies with a better trade-off between write amplification and average read amplification.

• 5. An empirical validation of a realistic cost model, which facilitates the design of merge policies via theoretical analysis and rapid simulation.

2 Policies studied

Bigtable (Google) The default for the Bigtable platform is as follows [35]. When the MemTable is flushed, if there are fewer than k SSTables, add a single new SSTable holding the MemTable contents. Otherwise, merge the MemTable with the i most recently created SSTables, where i is the minimum such that, afterwards, the size of each SSTable exceeds the sum of the sizes of all newer SSTables.¹ Roughly speaking, this tries to ensure that each SSTable is at most half the size of the next older SSTable. We denote this policy Bigtable.

Exploring (Apache HBase) Exploring is the default for HBase [5]. In addition to ${\varvec{k}}$, it has configurable parameters ${\varvec{\lambda }}$ (default 1.2), ${\varvec{C}}$ (default 3), and ${\varvec{D}}$ (default 10). When the MemTable (Memstore in HBase) is flushed, the policy orders the SSTables (HFiles in HBase) by time of creation, considers various contiguous subsequences of them, and merges one that is in some sense most cost-effective. Specifically: Temporarily add the MemTable as its own (newest) SSTable and then consider every contiguous subsequence s such that

• s has at least C and at most D SSTables, and

• in s, the size of the largest SSTable is at most $\lambda$ times the sum of the sizes of the other SSTables.

In the case that there is at least one such subsequence s, merge either the longest (if there are at most k SSTables) or the one with minimum average SSTable size (otherwise). In the remaining case, and only if there are more than k SSTables, merge a contiguous subsequence of C SSTables having minimum total size.

Fig. 1

Examples of SSTables states after 16 flushes for the 7 merge policies. SSTables are represented by rectangles (solid for the 6 stack-based policies, dotted for Leveled). Older SSTables are lower, newer SSTables are higher. Levels are represented by solid rectangles in the last plot. SSTables’ sizes are with respect to the flush size

Constant (AsterixDB before version 0.9.4) Constant is as follows. When the MemTable is flushed, if there are fewer than k SSTables, add a single new SSTable holding the MemTable contents. Otherwise, merge the MemTable and all k SSTables into one.

Tiered and Leveled Tiered policy is the default for Cassandra. Leveled is the default for LevelDB [21]. In theory, both policies have one core configurable parameter, the size ratio ${\varvec{B}}$. In practice, Tiered may need multiple parameters (3 in Cassandra) to determine SSTables of similar sizes, and Leveled also has an extra parameter that control the number of SSTables in level 0 as an on disk buffer. The total SSTable size in one tier or level is ${\varvec{B}}$ times larger than the previous tier or level. The differences are:

• In Tiered, every tier must have at most ${\varvec{B}}$ SSTables and each SSTable is ${\varvec{B}}$ larger than the SSTable size in the previous tier. In Leveled, all SSTables are of the same size and the number of SSTables in one level is ${\varvec{B}}$ more than the previous level.

• Any two SSTables can have overlapping key space in Tiered, while all SSTables must not have overlapping key space in the same level in Leveled

• Tiered only allows merging consecutive SSTables, while in Leveled, one SSTable is picked to be merged with all SSTables in the next level that have overlapping key ranges with the picked SSTable (if any). These SSTables do not have to be consecutive.

• In Tiered, every merge involves at least two SSTables. In Leveled, only one SSTable can be merged if there is no overlapping SSTable in the next level.

• Only one SSTable is created in a merge in Tiered. In Leveled, the number of SSTables created in a merge is typically the same as the number of SSTables being merged.

• In Tiered, the new SSTable size is typically the same as the total size of the SSTables being merged. In Leveled, all input and output SSTables have the same size.

Next are the definitions of the MinLatency and Binomial policies which were proposed by Mathieu et al [35]. First, define a utility function B, as follows. Consider any binary search tree T with some nodes $\{1,2,\ldots ,n\}$ in search tree order (each node is larger than those in its left subtree, and smaller than those in its right subtree). Given a node t in T, define its stack (merge) depth to be the number of ancestors smaller (larger) than t. (Hence, the depth of t in T equals its stack depth plus its merge depth.)

Fix any two positive integers k and m, and let $n = {\left( {\begin{array}{c}m + k\\ k\end{array}}\right) }-1$. Let $\tau ^*(m, k)$ be the unique n-node binary search tree on nodes $\{1,2,\ldots ,n\}$ that has maximum stack depth $k-1$ and maximum write depth $m-1$. For $t\in \{1,2,\ldots ,n\}$, define B(m, k, t) to be the stack depth of node t in T.

Compute the function B(m, k, t) via the following recurrence. Define B(m, k, 0) to be zero, and for $t>0$ use

$$\begin{aligned} B(m,k,t) = {\left\{ \begin{array}{ll} B(m-1,k,t) &{} \text {if } t <{\left( {\begin{array}{c}m + k - 1\\ k\end{array}}\right) }, \\ 1 + B\Big (m,k-1,t-{\left( {\begin{array}{c}m + k - 1\\ k\end{array}}\right) }\Big )&{} \text {if } t \ge {\left( {\begin{array}{c}m + k - 1\\ k\end{array}}\right) }. \end{array}\right. } \end{aligned}$$

The policies are defined as follows.

MinLatency For each $t=1,2,\ldots , n$, in response to the tth flush, the action of the policy is determined by t, as follows:

Let $m' = \min \{m : {\left( {\begin{array}{c}m + k\\ m\end{array}}\right) } > t\}$ and $i=B(m', k , t)$. Order the SSTables by time of creation, and merge the i-th oldest SSTable with all newer SSTables and the flushed MemTable (leaving i SSTables).

Binomial For each $t=1,2,\ldots , n$, in response to the tth flush, the action of the policy is determined by t, as follows:

Let $T_k(m) = \sum _{i=1}^m {\left( {\begin{array}{c}i + \min (i,k) - 1\\ i\end{array}}\right) }$ and $m' = \min \{m : T_k(m) \ge t\}$.

Let $i=1+B(m', \min (m',k) - 1, t - T_k(m'-1) - 1)$. Order the SSTables by time of creation, and merge the i-th oldest SSTable with all newer SSTables and the flushed MemTable (leaving i SSTables).

As described in Sect. 3, these policies are designed carefully to have the minimum possible worst-case write amplification among all policies in the aforementioned class of stack-based policies.

Bigtable, Constant, and (although it is not obvious from its specification) MinLatency are lazy—whenever the MemTable is flushed, if there are fewer than k SSTables, the policy leaves those SSTables unchanged and creates a new SSTable that holds just the flushed MemTable’s contents. For this reason, these policies tend to keep the number of SSTables close to k. In contrast, for moderate-length runs ($4^k$ or fewer flushes, as discussed later), Exploring and Binomial often merge multiple SSTables even when fewer than k SSTables are already present, so may keep the average number of SSTables well below k, potentially allowing faster read operations.

Examples of all these seven merge policies for the first 16 flushes are shown in Fig. 1. For the six stack-based policies (Fig. 1a–f), a new SSTable is added to the top of the stack in every flush. Several SSTables are merged into one SSTable. For example in Fig. 1a, before the 12th flush, there are 2 SSTables of size 2x and 2 SSTables of size 1x. After the 12th flush, all the 5 SSTables are merged into one big SSTable of size 12x. The number of SSTables of Bigtable, Binomial, Constant, Exploring, and MinLatency never exceeds $k = 4$. Binomial and MinLatency choose different SSTables to merge starting from the 9th flush, based on their own computations (Fig. 1b, e). For Tiered, a merge is triggered every $B=2$ flushes and multiple merges are triggered at the 4th, 8th, 12th, and 16th flush (Fig. 1f). For Leveled, multiple merges may be triggered at every flush starting from the 3rd flush, while only one merge is triggered at the 2nd flush (Fig. 1g). For example, before the 12th flush, there are 2 SSTables in level 1 (top rectangle), 4 rectangles in level 2, and 5 SSTables in level 3 (bottom rectangle). After the 12th flush, a new SSTable is added to level 1, triggering a merge which selects an SSTable in level 1 and merges it to level 2. Then, level 2 has 5 SSTables, and another merge is triggered which selects an SSTable in level 2 and merges it to level 3. Eventually, there are still 2 SSTables in level 1 and 4 SSTables in level 2, but 6 SSTables in level 3.

3 Design of MinLatency and Binomial

This section reviews definition of the class of so-called stack-based merge policies in [35], the worst-case write amplification metric, and how MinLatency and Binomial are designed to minimize that metric among all policies in that class.

3.1 Bounded depth stack-based merge policies

Informally, a stack-based policy must maintain a set of SSTables over time. The set is initially empty. At each time $t=1,2,\ldots ,n$, the MemTable is flushed, having current size in bytes equal to a given integer $\ell _t\ge 0$. In response, the merge policy must choose some of its current SSTables and then replace those chosen SSTables by a single SSTable holding their contents and the MemTable contents. As a special case, the policy may create a new SSTable from the MemTable contents alone. (The policy may replace additional sets of SSTables by their respective unions, but the policies studied here do not.)

Each newly created SSTable is written to the disk, batch-writing a number of bytes equal to its size, which by assumption is the sum of the sizes of the SSTables it replaces, plus $\ell _t$ if the merge includes the flushed MemTable. (This ignores updates and deletes, but see the discussion below.)

A bounded depth policy (in the context of a parameter k) must keep the SSTable count at k or below. Subject to that constraint, its goal is to minimize the write amplification, which is defined to be the total number of bytes written in creating SSTables, divided by $\sum _{t=1}^n\ell _t$, the sum of the sizes of the n MemTable flushes. (Write amplification is a standard measure in LSM systems [16, 30, 31, 40].) Tiered is stack-based but not bounded depth, while Leveled is neither stack-based nor bounded depth.

For intuition, consider the example $k=2$ and $\ell _t=1$ uniformly for $t\in \{1,2,\ldots ,n\}$. The optimal write amplification is $\Theta (\sqrt{n})$.

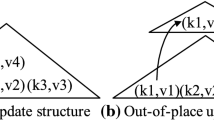
Next is the precise formal definition, as illustrated in Fig. 2a:

Problem 1

(k-Stack-Based LSM Merge) A problem instance is an $\ell \in \mathbb {R}_{+}^n$. For each $t\in \{1,\ldots ,n\}$, say flush t has (flush) size $\ell _t$. A solution is a sequence $\sigma =\{\sigma _1,\dots ,\sigma _n$}, called a schedule, where each $\sigma _t$ is a partition of $\{1,2,\ldots ,t\}$ into at most k parts, each called an SSTable, such that $\sigma _t$ is refined by²$\sigma _{t-1}\cup \{\{t\}\}$ (if $t\ge 2$). The size of any SSTable F is defined to be $\ell (F)=\sum _{t \in F} \ell _t$—the sum of the sizes of the flushes that comprise F. The goal is to minimize $\sigma$’s write amplification, defined as $W(\sigma ) = {\sum _{t=1}^n \delta (\sigma _t,\sigma _{t-1})}/{\sum _{t=1}^n \ell _t}$, where $\delta (\sigma _t,\sigma _{t-1}) = \sum _{F \in \sigma _t\setminus \sigma _{t-1}} \ell (F)$ is the sum of the sizes of the new SSTables created during the merge at time t.

Fig. 2

a An eager, stable schedule $\sigma$ ($n=6$, $k=3$). b A graphical representation of $\sigma$. Each shaded rectangle is an SSTable (over time). Row t is the stack at time t. c The binary-search-tree representation of $\sigma$

Formally, a (bounded depth) stack-based merge policy is a function P mapping each problem instance $\ell \in \mathbb {R}_{+}^n$ to a solution $\sigma$. In practice, the policy must be online, meaning that its choice of merge at time t depends only on the flush sizes $\ell _1, \ell _2, \ldots , \ell _t$ seen so far. Because future flush sizes are unknown, no online policy P can achieve minimum possible write amplification for every input $\ell$. Among possible metrics for analyzing such a policy P, the focus here is on worst-case write amplification: the maximum, over all inputs $\ell \in \mathbb {R}_{+}^n$ of size n, of the write amplification that P yields on the input. Formally, this is the function $n\mapsto \max \{ W(P(\ell )) : \ell \in \mathbb {R}_{+}^n\}$.

Updates and Deletes The formal definitions above ignore the effects of key updates and deletes. While it would not be hard to extend the definition to model them, for designing policies that minimize worst-case write amplification, this is unnecessary: These operations only decrease the write amplification for a given input and schedule, so any online policy in the restricted model above can easily be modified to achieve the same worst-case write amplification, even in the presence of updates and deletes.

Additional terminology Recall that a policy is stable if, for every input, it maintains the following invariant at all times among the current SSTables: the write times of all items in any given SSTable precede those of all items in every newer SSTable. (Formally, every SSTable created is of the form $\{i,i+1,\ldots ,j\}$ for some i, j.) As discussed previously, this can speed up reads. We note without proof that any unstable solution can be made stable while at most doubling the write amplification. Likewise, each uniform input has an optimal stable solution. All policies tested here are stable.

A policy is eager if, for every input $\ell$, for every time t, the policy creates just one new SSTable (necessarily including the MemTable flushed at time t). Every input has an optimal eager solution, and all bounded depth policies tested here except for Exploring are eager.

An online policy is static if each $\sigma _t$ is determined solely by k and t. In a static policy, the merge at each time t is predetermined—for example, for $t=1$, merge just the flushed MemTable; for $t=2$, merge the MemTable with the top SSTable, and so on—independent of the flush sizes $\ell _1, \ell _2,\ldots$ The MinLatency and Binomial policies are static. Static policies ignore the flush sizes, so it may seem counterintuitive that static policies can achieve optimum worst-case write amplification.

3.2 MinLatency and Binomial

Among bounded depth stack-based policies, MinLatency and Binomial, by design, have the minimum possible worst-case write amplification. Their design is based on the following relationship between schedules and binary search trees.

Fix any k-Stack-based LSM Merge instance $\ell =(\ell _1,\ldots ,\ell _n)$. Consider any eager, stable schedule $\sigma$ for $\ell$. (So $\sigma$ creates just one new SSTable at each time t.) Define the (rooted) merge forest ${\mathcal {F}}$ for $\sigma$ as follows: For $t=1,2,\ldots ,n$, represent the new SSTable $F_t$ that $\sigma$ creates at time t by a new node t in ${\mathcal {F}}$, and, for each SSTable $F_s$ (if any) that is merged in creating $F_t$, make node t the parent of the node s that represents $F_s$.

Next, create the binary search tree T for $\sigma$ from ${\mathcal {F}}$ as follows. Order the roots of ${\mathcal {F}}$ in decreasing order (decreasing creation time t). For each node in ${\mathcal {F}}$, order its children likewise. Then, let $T = T(\sigma )$ be the standard left-child, right-sibling binary tree representation of ${\mathcal {F}}$. That is, T and ${\mathcal {F}}$ have the same vertex set $\{1,2,\ldots ,n\}$, and, for each node t in T, the left child of t in T is the first (oldest) child of t in $\mathcal F$ (if any), while the right child of t in T is the right (next oldest) sibling of t in ${\mathcal {F}}$ (if any; here we consider the roots to be siblings). It turns out that (because $\sigma$ is stable) the nodes of T must be in search-tree order. (Each node is larger than those in its left subtree and smaller than those in its right subtree.) Figure 2a, c shows an example.

What about the depth constraint on $\sigma$, and its write amplification? Recall that the stack (merge) depth of a node t is the number of ancestors that are smaller (larger) than t. While the details are out of scope here, the following holds:

For any eager, stable schedule $\sigma$:

• 1. $\sigma$ obeys the depth constraint if and only if every node in $T(\sigma )$ has stack depth at most $k-1$,

• 2. the write amplification incurred by $\sigma$ on $\ell$ equals

$$\begin{aligned}&\frac{\sum _{t=1}^n ({\textsf {mergedepth}}(t, T(\sigma ))+1)\ell _t}{\sum _{t=1}^n \ell _t} \\&\quad \le 1+\max _{t=1}^n {\textsf {mergedepth}}(t, T(\sigma )). \end{aligned}$$

The mapping $\sigma \rightarrow T(\sigma )$ is invertible. Hence, any binary search tree t with nodes $\{1,2,\ldots ,n\}$, maximum stack depth $k-1$, and maximum merge depth $m-1$ yields a bounded depth schedule $\sigma$ (such that $T(\sigma ) = t$), having write amplification at most m on any input $\ell \in \mathbb {R}_{+}^n$.

Rationale for MinLatency MinLatency uses this observation to produce its schedule [35]. First consider the case that $n={\left( {\begin{array}{c}m + k\\ k\end{array}}\right) }-1$ for some integer m. Among the binary search trees on nodes $\{1,2,\ldots ,n\}$, there is a unique tree with maximum stack depth $k-1$ and maximum merge depth $m-1$. Let $\tau ^*(m, k)$ denote this tree, and let $\sigma ^*(m, k)$ denote the corresponding schedule.

MinLatency is designed to output $\sigma ^*(m, k)$ for any input of size n. Since $\tau ^*(m, k)$ has maximum merge depth $m-1$, as discussed above, $\sigma ^*(m, k)$ has write amplification at most m, which by calculation is

$$\begin{aligned} (1+O(1/k))\, k\, n^{1/k}/c_k, \end{aligned}$$

(1)

where $c_k = (k + 1)/(k!)^{1/k} \in [2,e]$. This bound extends to arbitrary n, so MinLatency ’s worst-case write amplification is at most (1).

This is optimal, in the following sense: For every $\epsilon >0$ and large n, no stack-based policy achieves worst-case write amplification less than $(1-\epsilon ) k\, n^{1/k}/c_k$. This is shown by using the bijection described above to bound the minimum possible write amplification for uniform inputs.

Binomial and the small-n and large-n regimes As mentioned previously, due to the fact that MinLatency and Bigtable are lazy, they produce schedules whose average SSTable count is close to k. When n is large, any policy with near-optimal write amplification must do this. Specifically, in what we call the large-n regime—after the number of flushes exceeds $4^k$ or so—any schedule with near-optimal write amplification (e.g., for uniform $\ell$) must have average SSTable count near k. In this regime, Binomial behaves similarly to MinLatency. Consequently, in this regime, Binomial still has minimum worst-case write amplification.

However, in what we call the small-n regime—until the number of flushes n reaches $4^k$—it is possible to achieve near-optimal write amplification while keeping the average SSTable count somewhat smaller. Binomial is designed to do this [35]. In the small-n regime, it produces the schedule $\sigma$ for the tree $\tau ^*(m, m)$, for which the maximum stack depth and maximum merge depth are both $m\approx \log _2 (n)/2$, so Binomial ’s average SSTable count and write amplification are about $\log _2 (n)/2$, which is at most k (in this regime) and can be less. Consequently, in the small-n regime, Binomial can opportunistically achieve average SSTable count well below k. In this way, it compares well to Exploring, and it behaves well even with unbounded depth ($k=\infty$).

4 Experimental evaluation

4.1 Test platform: AsterixDB

Apache AsterixDB [2, 6] is a full-function, open-source big data management system (BDMS), which has a shared-nothing architecture, with each node in an AsterixDB cluster managing one or more storage and index partitions for its datasets based on LSM storage. Each node uses its memory for a mix of storing MemTables of active datasets, buffering of file pages as they are accessed, and other memory-intensive operations. AsterixDB represents each SSTable as a $B^+$-tree, where the number of keys at each internal node is roughly the configured page size divided by the key size. (Internal nodes store keys but not values.) Secondary indexing is also available using $B^+$-trees, R-trees, and/or inverted indexes [3]. As secondary indexing is out of the scope of this paper, our experiments involve only primary indexes.

AsterixDB provides data feeds for rapid ingestion of data [23]. A feed adapter handles establishing the connection with a data source, as well as receiving, parsing, and translating data from the data source into ADM objects [2] to be stored in AsterixDB. Several built-in feed adapters available for retrieving data from network sockets, local file system, or from applications like Twitter and RSS.

4.2 Experimental setup

The experiments were performed on a machine with an Intel i3–4330 CPU running CentOS 7 with 8 GB of RAM and two mirrored (RAID 1) 1 TB hard drives. AsterixDB was configured to use 1 node controller, so all records are stored on the same disk location. The relatively small RAM size of 8 GB limits caching, to better simulate large workloads. The MemTable capacity was configured at 4 MB. The small MemTable capacity increases the flush rate to better simulate longer runs.

The workload was generated using the Yahoo! Cloud Serving Benchmark (YCSB) [11, 44], with default parameters used in load phase. The full workload consists of 80,000,000 writes, each writing one record with a primary key of 5 to 23 bytes plus 10 attributes of 100 bytes each, giving 11 attributes of about 1 KB total size. Each primary key is a string with a 4-byte prefix and a long integer (as a string). Insert order was set to the default hashed.

To achieve high ingestion rate, we implemented a YCSB database interface layer for AsterixDB using the “socket_adapter” data feed (which retrieves data from a network socket) with an upsert data model, so that records are written without a duplicate key check to achieve a much higher throughput. Upsert in AsterixDB and Cassandra is the equivalent of standard insert in other NoSQL systems, where, if an inserted record conflicts in the primary key with an existing record, it overwrites it.

The MemTable flushes were triggered by AsterixDB when the MemTable was near capacity, so the input $\ell$ generated by the workload was nearly uniform, with each flush size $\ell _t$ about 4 MB. This represents about 3300 records per flush, so the input size n—the total number of flushes in the run—was just over 24,000.

For each of the five bounded depth stack-based policies tested, and for each $k\in \{3, 4, 5, 6, 7, 8, 10\}$, we executed a single run testing that policy and configured with that depth (SSTable count) limit k. For Tiered and Leveled policies, we executed the same runs with size ratio $B\in \{4, 8, 16, 32\}$, the number of SSTables in level 0 was set to 2 in Leveled policy. Leveled also used a strategy that picks the SSTable which overlaps with the minimum number of SSTables in the next level for merges in order to reduce the write amplification. All other policy parameters were set to their default values. (See Sect. 2.) Each of the 43 runs started from an empty instance and then inserted all records of the workload into the database, generating just over 24,000 flushes for the merge policy.

For some smaller k values, some of the bounded depth policies had significantly large write amplification and so did not finish the run. Binomial and MinLatency finished in about 16 hours, but Bigtable and Exploring ingested less than 40% of the records after two days, so were terminated early. Similarly, Constant was terminated early in all of its runs.

As our focus is on write amplification, which is not affected by reads, the workload contains no reads. (But see Sect. 4.3.2.)

The data for all 43 runs are tabulated in “Appendix A.”

Fig. 3

Write amplification versus number of flushes over time for runs with $k\in \{5,6,7\}$. The top row shows $n\approx 24{,}000$; the bottom shows $n =2000$. The transition from the small-n regime to the large-n regime (if present) occurs at $4^k$ flushes. Complete data are in “Appendix A”

4.3 Policy comparison

4.3.1 Write amplification

At any given time t during a run, define the write amplification (so far) to be the total number of bytes written to create SSTables so far divided by the number of bytes flushed so far ($\sum _{s=1}^t \ell _s$). This section illustrates how write amplification grows over time during the runs for the various policies. The 5 bounded depth stack-based policies all share a common parameter k, which is the maximum number of SSTables. On the other hand, Tiered and Leveled both share a different parameter B, which is the size ratio between tiers or levels. Because these two parameters carry different meanings, it is not meaningful to compare the write amplification of these 7 policies directly with the same value of k and B. Thus, in this subsection, we compare and evaluate them into 2 groups: One group containing the 5 bounded depth stack-based policies are compared for the same value of k, while the other group of Tiered and Leveled are compared for the same value of B.

4.3.2 Bounded depth stack-based policies

We focus on the runs with $k\in \{5,6,7\}$, which are particularly informative. The runs for each k are shown in Fig. 3a–c, each showing how the write amplification grows over the course of all $n\approx 24{,}000$ flushes. Because workloads with at most a few thousand flushes are likely to be important in practice, Fig. 3d–f repeats the plots, zooming in to focus on just the first 2000 flushes ($n=2000$).

In interpreting the plots, note that the caption of each sub-figure shows the threshold $4^k$. The small-n regime lasts until the number of flushes passes this threshold, whence the large-n regime begins. Note that (depending on n and k) some runs lie entirely within the small-n regime ($n\le 4^k$), some show the transition, and in the rest (with $n\gg 4^k$) the small-n regime is too small to be seen clearly. In all cases, the results depend on the regime as follows. During the small-n regime, MinLatency has smallest write amplification, with Binomial, Bigtable, and then Exploring close behind. As the large-n regime begins, MinLatency and Binomial become indistinguishable. Their write amplification at time t grows sub-linearly (proportionally to $t^{1/k}$), while those of Bigtable and Exploring grow linearly (proportionally to t). Although we do not have enough data for Constant, its write amplification is O(t/k) as it merges all SSTables in every k flushes. These results are consistent with the analytical predictions from the theoretical model [35].

4.3.3 Tiered policy and Leveled policy

The runs for Tiered and Leveled are shown in Fig. 4a for $n \approx 24{,}000$ flushes with $B \in \{4, 8, 16, 32\}$. Tiered achieved lowest write amplification than any other policy tested, while Leveled has significantly higher write amplification than all the other policies except for Constant. The write amplification is $O (\log t)$ and $O(B \log t)$ for Tiered and Leveled, respectively. From the figure, it is observable that smaller size ratio leads to higher write amplification in Tiered but lower write amplification in Leveled, which verifies the theoretical numbers. Runs with 2000 flushes are shown in Fig. 4b which shows the same results. Unlike the bounded depth policies, the small-n regime does not apply to Tiered and Leveled.

Fig. 4

With $B \in \{4, 8, 16, 32\}$, Tiered are shown as solid lines in the top sub-figures, Leveled are shown as dashed lines in the bottom sub-figures

4.3.4 Read amplification

Read amplification is the number of disk I/Os per read operation. In this paper, we focus on point query only. In practice, accessing one SSTable only costs one disk I/O, assuming all metadata and all internal nodes of $B^+$-trees are cached. Therefore, the worst-case read amplification can be computed as the SSTable count for all stack-based policies, or approximately the number of levels for Leveled policy (number of SSTables in level 0 is 2 in our experiments), although techniques such as Bloom filter can skip checking most of the SSTables, making the actual read amplification be only 1.

As noted previously, MinLatency and Bigtable, being lazy, tend to keep the read amplification near its limit k. In the large-n regime, any policy that minimizes worst-case write amplification must do this. But, in the small-n regime, Binomial opportunistically achieves smaller average read amplification, as does Exploring to some extent.

Figure 5 shows a line for each policy except Constant. The line for Constant was generated from simulation. It can be clearly seen from the figure that Constant is far from optimal; thus, below we concentrate on the other policies. The curve shows the trade-off between final write amplification and average read amplification achieved by its policy: It has a point (x, y) for every run of the bounded depth stack-based policy with $k \in \{4, 5, 6, 7, 8, 10\}$, or Tiered and Leveled with $B\in \{4, 8, 16, 32\}$ (and $n\approx 24{,}000$), where x is the final write amplification for the run and y is the average read amplification over the course of the run. Both the x-axis and y-axis are log-scaled.

Fig. 5

Average read amplification versus total write amplification (x and y log-scaled)

First consider the runs with $k\in \{7,6,5,4\}$. Within each curve, these correspond to the four rightmost/lowest points (with $k=4$ being rightmost/lowest). These runs are dominated by the large-n regime, and each policy has average SSTable count (y coordinate) close to k. In this regime, the Binomial and MinLatency policies achieve the same (near-optimal) trade-off, while the Exploring and Bigtable policies are far from the optimal frontier due to their larger write amplification.

Next consider the remaining runs, for $k\in \{10,8\}$. On each curve, these are the two leftmost/highest points, with $k=10$ leftmost. In the curve for Exploring, its two points are indistinguishable. These runs stay within the small-n regime. In this regime, Binomial achieves a slightly better trade-off than the other policies. MinLatency and Bigtable give comparable trade-offs. For Exploring, its two runs lie close to the optimal frontier, but low: increasing the SSTable limit (k) from 8 to 10 makes little difference.

The read amplification of Tiered and Leveled is inverse of their write amplification, that is $O(B \log t)$ for Tiered and $O(\log t)$ for Leveled. Tiered—the 4 points from left to right correspond to $B \in \{32, 16, 8, 4\}$, respectively—has higher read amplification than any other policy tested but has significantly lower write amplification. Leveled—the 4 points from left to right correspond to $B \in \{4, 8, 16, 32\}$, respectively—has comparable read amplification to the other policies except Tiered, but has much higher write amplification. Usually, a merge policy cannot achieve low write and read amplification at the same time. Most researches tried to improve the trade-off curve of Tiered and Leveled such that it can get closer to the optimal frontier [13, 14]. As shown in the figure, Binomial and MinLatency are both closer to the optimal frontier, which has better trade-off between write and read. Bigtable and Exploring are closer to the optimal frontier with a few large k values, but they have to pay very high write cost to reduce the read cost.

4.3.5 Transient space amplification

Recently, various works [7, 16, 28] have discussed the importance of space amplification. In an LSM-tree based database system, space amplification is mostly determined by the amount of obsolete data from updates and deletions in a stable state which are yet to be garbage-collected in merges. Because our primary focus is an append-only workload without any updates or deletions, there would be no obsolete data, so the space amplification of all policies would be almost the same. Therefore, comparing space amplification among these policies is not interesting here.

On the other hand, what is more interesting is the transient space amplification, which measures the temporary disk space required for creating new components [18, 33] during merges. We compute transient space amplification as the maximum total size of all SSTables divided by the total data size flushed (inserted) so far. For example, a flush in Tiered or Leveled can trigger several merges in sequence, where only the largest merge will be counted. A maximum of transient space amplification of 2 can happen when a major merge involves all existing SSTables. A policy with higher transient space amplification needs larger disk space to load the same amount of data, causing lower disk space utilization. The highest transient space amplification observed in our experiments for each policy is shown in Fig. 6, where Binomial, MinLatency, Bigtable, and Exploring use $k = 4$, Tiered uses $B=4$, and Leveled uses $B=32$. All stack-based policies tested (including Tiered) could eventually reach a transient space amplification of 2, while Leveled has very low transient space amplification that is close to 1, and hence utilizes disk space much better. Among the five stack-based policies, Tiered offered lowest transient space amplification but highest read amplification; the transient space amplification is lower than the others for Bigtable, but its write amplification is high. But in general, any policy which tries to reduce the total number of SSTables to a minimum can have a high transient space amplification close to 2 due to major merges.

Fig. 6

Transient space amplification of stack-based policies with $k=4$ or $B=4$ and Leveled with $B=32$

4.4 Updates and deletions

Update and delete operations insert records whose keys already occur in some SSTable. As a merge combines SSTables, if it finds multiple records with the same key, it can remove all but the latest one. Hence, for workloads with update and delete operations, the write amplification can be reduced. But the experimental runs described above have no update or delete operations. As a step toward understanding their effects, we did additional runs with $k=6$ and $B \in \{4, 8, 16, 32\}$, with 70% of the write operations replaced by updates, each to a key selected randomly from the existing keys according to a Zipf distribution with exponent $E=0.99$, concentrated on the recently inserted items, similar to the “Latest” distribution in YCSB. The flush rate is reduced, as updates to keys currently in the MemTable are common but do not increase the number of records in the MemTable. To compensate, we increased the total number of operations by 50%, resulting in about $n\approx 26,400$ flushes.

Figure 7a, b plots the write amplification versus flushes for the 4 runs of the bounded depth policies and for the 8 runs of Tiered and Leveled, respectively.

Fig. 7

Runs with random updates ($n\approx 26,400$)

The primary effect (not seen in the plots) is a reduction in the total number of flushes, but the write amplification (even as a function of the number of flushes) is also somewhat reduced, compared to the original runs (Fig. 3b). The relative performance of the various policies is unchanged. Experiments with other key distributions (uniform over existing keys, or Zipf concentrated on the oldest) yielded similar results that we do not report here.

Although the theoretical model mostly focuses on the append-only workload, via the experiments shown in Fig. 7, the write amplifications are still aligned with the model’s prediction even with a update-heavy workload. In practice, with more updates or deletions, the error between the theoretical and the actual write cost of Binomial and MinLatency can become more and more significant. One way to solve this problem is to periodically re-evaluate the current status of SSTables and recompute the number of flushes based on the total SSTable size. Hence, Binomial and MinLatency are still good candidates even for update-heavy workloads in real-world applications.

4.5 Insertion order

Unlike stack-based policies where merges are independent of SSTable contents, Leveled is highly sensitive to the insertion order, which affects the number of overlapping SSTables in every merge. For workloads with sequentially inserted keys, SSTables do not overlap with each other, and hence they are simply moved to the next level by updating only the metadata with no data copy [38]. For an append-only workload with sequential insertion order, Leveled can achieve a minimum write amplification that is close to 1, as all merges are just movements of SSTables. However, if updates or deletions were added to such workload, we found that Leveled could have very similar write amplification as a workload with non-sequential insertion order. We reran the same experiments for Leveled with updates, except that we changed the insert order from hashed to ordered, such that new keys inserted are in sequential order, while some of the inserted keys can be updated later. Results of these runs are shown in Fig. 8, which is almost identical to Fig. 7b. The insertion order does not impact the write amplification of the other stack-based policies by much; thus, we do not report their write amplifications here.

A minor observation from these runs is, compared to the runs with hashed insertion order, the total number of flushes is slightly reduced, leading to a slightly lower write amplification. This is because AsterixDB implements MemTable as $B^+$-tree. The MemTables are usually 1/2 to 2/3 full with hashed, so flushes are triggered more often. As SSTables are created using bulk loading method, their $B^+$-tree fill factors are very high, making the flushed SSTable size smaller than the MemTable size. For a workload with sequential insertion order, both MemTables and SSTables have very high fill factors, so flushes are triggered less frequently.

Fig. 8

Runs of sequential insertion with random updates for Leveled ($n\approx 26,400$)

5 Model validation and simulation

In each run, the total time spent in each merge operation is well predicted by the bytes written. This is demonstrated by the plot in Fig. 9, which has a point for every individual merge in every run, showing the elapsed time for that merge versus the number of bytes written by that merge.

Fig. 9

Time for each merge versus bytes written

Also, observed write amplification is in turn well predicted by the theoretical model. More specifically, using the assumptions of the theoretical model, we implemented a simulator [42] that can simulate a given policy on a given input for any stack-based policies. For each of the 35 runs of the bounded depth policies from the experiment, we simulated the run (for the given policy, k, and $n\approx 24{,}000$ uniform flushes).

Figure 10a illustrates the five runs with $k=7$, over time, by showing the write amplifications over time as observed in the actual runs. Figure 10b shows the same for the simulated runs. For the static policies MinLatency and Binomial, the observed write amplification tracks the predicted write amplification closely. For Exploring and Bigtable, the observed write amplification tracks the predicted write amplification, but not as closely. (For these policies, small perturbations in the flush sizes can affect total write amplification.)

Fig. 10

Observed and simulated write amplification over time

Fig. 11

Observed versus simulated write amplification. The bottom plot zooms in to the portion with $x \in [7, 39]$

Figure 11 shows that the simulated write amplification is a reasonable predictor of the write amplification observed empirically. That figure has two plots. The first (top) plot in that figure has a curve for each policy (except Constant), with a point for each of the six or seven runs that the policy completed, showing the observed final write amplification versus the simulated final write amplification. The two extreme points in the upper right are for Bigtable and Exploring with $k=4$, with very high write amplification. To better show the remaining data, the second (bottom) plot expands the first, zooming in to the lower left corner (the region with $x\in [7, 39]$). For each curve, the $R^2$ value of the best-fit linear trendline is shown in the upper left of the first plot. (The trendlines are not shown.) The $R^2$ values are very close to 1, demonstrating that the simulated write amplification is a good predictor of the experimentally observed write amplification.

Policy design via analysis and simulation

Fig. 12

Simulated total write amplification for 100,000 flushes (and 1,000,000 for $k=10$)

A realistic theoretical model facilitates design in at least two ways. As described earlier, the model allows a precise theoretical analysis of the underlying combinatorics, as illustrated by the design of MinLatency and Binomial. It also allows accurate simulation. As noted in the Introduction, LSM systems are designed to run for months, incorporating terabytes of data. Even with appropriate adaptations, real-world experiments can take days or weeks. Replacing experiments by (much faster) simulations can moderate this bottleneck. As a proof of concept, Fig. 12 shows simulated write amplification over time for Bigtable, Binomial, Constant, Exploring, and MinLatency for $k\in \{6,7,10\}$. As these policies’ average read amplification are all less than k ($\frac{k}{2}$ for Constant), the following settings were used for Tiered and Leveled to achieve similar average read amplification (assuming one SSTable overlaps with B SSTables in the next level in every merge for Leveled):

• Figure 12a: $k = 6$, $n = 100{,}000$,$B = 2$ for Tiered and $B = 9$ for Leveled, their average read amplification are 8.15 and 6.25, respectively;

• Figure 12b: $k = 7$, $n = 100{,}000$, $B = 2$ for Tiered and $B = 6$ for Leveled, their average read amplification are 8.15 and 7.33, respectively;

• Figure 12c: $k = 10$, $n = 1{,}000{,}000$, $B = 2$ for Tiered and $B = 9$ for Leveled, their average read amplification are 9.88 and 10.53, respectively.

The smallest size ratio allowed for Tiered is 2, which also provides the lowest average read amplification it can achieve. In all settings, the write amplification of Leveled is 3 to 4 times larger than Binomial and MinLatency; they are only comparable with Exploring and slightly better than Bigtable in the first plot. Tiered, on the other hand, had lower write amplification than Bigtable and Exploring, but always higher than Binomial and MinLatency, and its average read amplification is higher too, except for the last plot, which is slightly lower than 10.

These simulations took only minutes to complete.

6 Discussion

As predicted by the theoretical model, policy behavior fell into two regimes: the small-n regime (until the number of flushes reached about $4^k$) and the large-n regime (after that). MinLatency achieved the lowest write amplification, with Binomial a close second to it. Bigtable and Exploring were not far behind in the small-n regime, but in the large-n regime their write amplification was an order of magnitude higher. In short, the two newly proposed policies achieve near-optimal worst-case write amplification among all stack-based policies, outperforming policies in use in industrial systems, especially for runs with many flushes.

The trade-offs between write amplification and average read amplification were also studied in this paper. In the large-n regime, all bounded depth policies except (sometimes) Exploring had average read amplification near k. MinLatency and Binomial, but not Exploring or Bigtable, were near the optimal frontier. In the small-n regime, all policies were close to the optimal frontier, with Binomial and Exploring having average read amplification below k. On the other hand, although popular in the literature, the trade-offs of Tiered and Leveled are much worse than Binomial and MinLatency. These two policies might be overrated if we focus more on the cost of writes and reads.

6.1 Limitations and future work

Non-uniform flush sizes, update s, dynamic policies. The experiments here are limited to near-uniform inputs, where most flush sizes are about the same. Most LSM database systems, including AsterixDB, Cassandra, HBase, LevelDB, and RocksDB, use uniform flush size. Some of them support checkpointing, which flushes the MemTable at some timeout interval, or when the commit log is full, potentially creating smaller SSTable before the MemTable is full. Although uniform or near-uniform flush is more common in the literature, workloads with variable flush sizes are of interest. Variable flush size may be used to coordinate multiple datasets sharing the same memory budget, or balance the write buffer and the read buffer cache for dynamic workloads. For example, a recent work [32] described an architecture which provides adaptive memory management to minimize overall write costs. For moderately variable flush sizes, we expect the write amplification of most policies (and certainly of MinLatency and Binomial) to be similar to that for uniform inputs. Regardless of variation, the write amplification incurred by MinLatency and Binomial is guaranteed to be no worse than it is for uniform inputs.

Most of the experiments here are limited to append-only workloads. A few preliminary results here suggest that a moderate to high rate of updates and deletes mainly reduce flush rate and slightly reduce write amplification. At a minimum, updates and deletes are guaranteed not to increase the write amplification incurred by MinLatency and Binomial. But inputs with updates, deletes, and non-uniform flush sizes can have optimal write amplification substantially below the worst case of $\Theta (n^{1/k})$. In this case, dynamic policies such as Bigtable, Exploring, and new policies which are designed using the theoretical framework of competitive-analysis (as in [35]), may, in principle, outperform static policies such as Binomial and MinLatency. Future work will explore how significant this effect may be in practice. On the other hand, all the six evaluated stack-based policies are not very sensitive to workloads with updates or deletes; their relative ranking of write and read cost almost remains the same. The exception is Leveled, which is very sensitive to updates or deletes if the insertion order is nearly sequential. With a very low rate of updates or deletes, write amplification of Leveled increased significantly.

Compression Many databases support data compression to reduce the data size on disk, at a cost of higher CPU usage to retrieve data with decompression. In general, a system with stronger compression has lower write amplification and space amplification because of smaller data size [16]. Moreover, compression makes flushed SSTable size smaller than the MemTable size which can potentially affect the performance of Binomial and MinLatency.

Read costs The experimental design here focuses on minimizing write amplification, relying on the bounded depth constraint to control read costs such as read amplification—the average number of disk accesses required per read for point queries. Most LSM systems (other than Bigtable) offer merge policies that are not depth-bounded, instead allowing the SSTable count to grow, say, logarithmically with the number of flushes. A natural objective would be to minimize a linear combination of the read and write amplification— this could control the stack depth without manual configuration. (This is similar to Binomial ’s behavior in the small-n regime, where it minimizes the worst-case maximum of the read and write amplification, achieving a reasonable balance.) For read costs, a more nuanced accounting is desirable: It would be useful to take into account the effects of Bloom filters, and dynamic policies that respond to varying rates of reads are also of interest. Moreover, read amplification of point queries or range queries, query response time and throughput, sequential versus random access to SSTables can be of interest as well.

Secondary indexes The existence of secondary indexes impacts merging. For example, AsterixDB (with default settings) maintains a one-to-one correspondence between the SSTables for the primary indexes and the SSTables for the secondary indexes. Ideally, merge policies should take secondary indexes into account.

7 Related work

Historically, the main data structure used for on-disk key value storage is the $B^+$-tree. Nonetheless, LSM architectures are becoming common in industrial settings. This is partly because they offer substantially better performance for write-heavy workloads [24]. Further, for many workloads, reads are highly cacheable, making the effective workload write-heavy. In these cases, LSM architectures substantially outperform $B^+$-trees.

In 2006, Google released Bigtable [9, 20], now the primary data store for many Google applications. Its default merge policy is a bounded depth stack-based policy. We study it here. Spanner [12], Google’s Bigtable replacement, likely uses a stack-based policy, though details are not public.

Apache HBase [5, 19, 27] was introduced around 2006, modeled on Bigtable, and used by Facebook 2010–2018. Its default merge policy is Exploring, the precursor of which was a variant of Bigtable called RatioBased. Both policies are configurable as bounded depth policies. Here, we report results only for Exploring, as it consistently outperformed RatioBased.

Apache Cassandra [4, 29] was released by Facebook in 2008. Its first main merge policy, SizeTiered, is a stack-based policy that orders the SSTables by size, groups similar-sized SSTables, and then merges a group that has sufficiently many SSTables. SizeTiered is not stable—that is, it does not maintain the following property at all times: the write times of all items in any given SSTable precede those of all items in every newer SSTable. With a stable policy, a read can scan the recently created SSTables first, stopping with the first SSTable that contains the key. Unstable policies lack this advantage: A read operation must check every SSTable. Apache Accumulo [26] which was created in 2008 by the NSA uses a similar stack-based policy. We do not test these policies here, as our test platform supports only stable policies, and we believe they behave similarly to Bigtable or Exploring.

Previous to this work, our test platform—Apache AsterixDB—provided just one bounded depth policy (Constant), which suffered from high write amplification [3]. AsterixDB has removed support for Constant, and, based on the preliminary results provided here, added support for Binomial. Our recent work [34] shows that Binomial can provide superior write and read performance for LSM secondary spatial indexes, too.

Leveled policies LevelDB [15, 21] was released in 2011 by Google. Its merge policy, unlike the policies mentioned above, does not fit the stack-based model. For our purposes, the policy can be viewed as a modified stack-based policy where each SSTable is split (by partitioning the key space into disjoint intervals) into multiple smaller SSTables that are collectively called a level (or sorted run). Each read operation needs to check only one SSTable per level—the one whose key interval contains the given key. Using many smaller tables allows smaller, “rolling” merges, avoiding the occasional monolithic merges required by stack-based policies.

In 2011, Apache Cassandra added support for a leveled policy adapted from LevelDB. (Cassandra also offers merge policies specifically designed for time-series workloads.) In 2012, Facebook released a LevelDB fork called RocksDB [16, 17]. RocksDB offers several policies: the standard Tiered and Leveled, Leveled-N which allows multiple sorted runs per level, a hybrid of Tiered+Leveled, and FIFO which aims for cache-like data [18].

Mixed of tiered and leveled policies In the literature, Tiered provides very low write amplification but very high read amplification. On the other hand, Leveled provides good read amplification at the cost of high write amplification. It is natural to combine these 2 policies together to achieve a more balanced trade-off between write and read amplification. In RocksDB [16, 17], there are 2 policies of such mix of Tiered and Leveled policies. The Leveled-N policy allows N sorted run in a single level instead of 1 sorted run per level. Similar idea was also described in [13, 14]. The other policy is called tiered+leveled, which uses Tiered for the smaller levels and Leveled for the larger levels. This policy allows transition from Tiered to Leveled at a certain level. SlimDB [39] is one example of this policy. It is an interesting research direction to evaluate and compare their trade-offs between write and average read amplification with Binomial and MinLatency.

None of the leveled or mixed policies are stack-based or bounded depth policies.

Other merge policy models and optimizations Independently of Mathieu et al. [35], Lim et al. [30] propose a similar theoretical model for write amplification and point out its utility for simulation. The model includes a statistical estimate of the effects of for updates and deletes. For leveled policies, Lim et al. use their model to propose tuning various policy parameters—such as the size of each level—to optimize performance. Dayan et al. [13, 14] propose further optimizations of SizeTiered and leveled policies by tuning aspects such as the Bloom filters’ false positive rate (vs. size) according to SSTable size, the per-level merge frequency, and the memory allocation between buffers and Bloom filters.

Multi-threaded merges (exploiting SSD parallelism) are studied in [10, 16, 31, 43]. Cache optimization in leveled merges is studied in [41]. Offloading merges to another server is studied in [1].

Some of the methods above optimize read performance; those complement the optimization of write amplification considered here. None of the above works consider bounded depth policies.

This paper focuses primarily on write amplification (and to some extent read amplification). Other aspects of LSM performance, such as I/O throughput, can also be affected by merge policies but are not discussed here. For a more detailed discussion of LSM architectures, including compaction policies, see [33].

8 Conclusions

This work compares several bounded depth LSM merge policies, including representative policies from industrial NoSQL databases and two new ones based on recent theoretical modeling, as well as the standard Tiered policy and Leveled policy, on a common platform (AsterixDB) using Yahoo! cloud serving benchmark. The results have validated the proposed theoretical model and show that, compared to existing policies, the newly proposed policies can have substantially lower write amplification. Tiered and Leveled, while popular in the literature, generally underperform because of their worse trade-off between writes and reads. The theoretical model is realistic and can be used, via both analysis and simulation, for the effective design and analysis of merge policies. For example, we shared our experimental findings with the developers of Apache AsterixDB [6], and Binomial, designed via the theoretical model, has now been added as an LSM merging policy option to AsterixDB.

Appendix (Data)

For each of the 43 runs, Table 1 shows the total write amplification and the average read amplification at five points during the run: after 1000, 3000, 5000, 10,000, and 20,000 flushes. If it happens that the MemTable is flushed while a merge is ongoing, the SSTable count may briefly exceed k. For this reason, the average read amplification slightly exceeded k in a few runs (with $k\in \{3,4,5\}$—see the bold numbers).

Table 1 Total observed write amplification and average read amplification for all runs, for various n