1 Introduction

Numerical modeling and simulation techniques are essential for many engineering applications. This technique evolved and played a major role in the industry and institutions for past few decades. The marine vehicles such as an underwater robotic vehicle (URV) for sub-sea exploration and installation have increased in the past few decades. The remotely operated vehicles (ROVs) are the major workhorses to carry out several tasks in deeper and riskier areas where the use of human divers is impractical. However, there are some challenges in operating the ROVs precisely; such as unpredictable disturbances like current and waves in its operating environment.

The maneuverability becomes essential tasks in designing the ROV. A typical marine vessel control system has three independent blocks denoted as guidance, navigation, and control system (GNC). A dynamics model of an ROV for designing the GNC [1] is required. Unfortunately, the six degrees of freedom (DoF) dynamics model of the ROV [2,3,4,5] is harder to model than the streamlined autonomous underwater vehicle (AUV) [6,7,8,9,10,11,12,13,14,15] which exists an analytical solution for the hydrodynamics parameters.

Traditionally, the hydrodynamic parameters and the underwater response of the ROV are determined using a lab-based experimental approach. However, this method is quite costly, time-consuming and subject to the availability of the test facilities and an adequate scale model. With the recent advancement in computer technology, the computational fluid dynamic (CFD) has been widely used for the URV [6, 8, 12,13,14, 16].

A towing tank test for seakeeping tests and other tests performed with free-running models is used to determine the scale model dynamics. The Froude Similitude Laws are used on the scale model to study the flow pattern around it. A planar motion mechanism (PMM) and marine dynamic test laboratory facility are used on a real or scale model to determine the hydrodynamics coefficients of the ROV model in all DoF. Besides using the lab-based approach, a recent approach which used a pulley system [17] attached near a water tank was designed to compute the hydrodynamics coefficients of a scale model. However, the errors in computation were around 30%. Also, it was more suitable for a small and streamlined design due to the constraints of the pulley system and water tank.

Recently, a pendulum type of free-decaying experiment [4, 5] on a scale ROV model was used to determine the hydrodynamic coefficients. The scale-up results were compared using the CFD software and pool test. The simulations have achieved a reasonable agreement with the experimental data in some DoFs. Subsequently, another free-decaying method using four springs [18] attached to the ROV was proposed. It enables the hydrodynamic coefficients in both longitudinal and lateral hydrodynamic coefficients to be determined. However, the linear hydrodynamics damping terms could only be estimated. The error between real and estimated value was approximately 20–30%. Another approach uses system identification way such as adaptive and least-square-based estimation to estimate the parameters of the ROV. It was applied to the following ROVs namely: ROV Hylas [19], ROMEO [2], Johns Hopkins University ROV (JHUROV) [20], C-SCOUT AUV [21] and VideoRay ROV [22]. The results showed the adaptive method was able to predict the ROV motion better than the least-square method. However, both approaches required a sea trial that unfortunately depended on the test site availability and the presence of a completed ROV with the control system design implemented.

Hence, an alternative approach to determining the hydrodynamic model of the ROV. The following CFD software namely: ANSYS-FLUENT™ [16], ANSYS-CFX™ [12] and Phoenics™ [6] have been used. The CFD simulations have shown to be quite successful in simulating the streamlined underwater vehicles such as AUV but commonly performed on a complex-shaped ROV. The estimation of the hydrodynamics coefficients of an ROV [3,4,5] was performed using ANSYS-CFX™ and FLUENT™ and later verified by experiments in water with approximately 20% error. However, the prediction of the hydrodynamics parameters of the ROV continues to face difficulty due to the complexity and variability of the ROV’s geometry and fluid flow around its non-streamlined body for the initial stage of control system design.

In this paper, the hydrodynamic damping parameters are obtained using STAR-CCM+™ followed by a systematic approach of using CAD software MULTISURF™ to model and discretize the ROV for the Wave Analysis MIT (WAMIT™) [23] to determine the hydrodynamic added mass. The MATLAB™ will provide a routine to extract all the information generated by WAMIT™ to determine the added mass coefficients of the vehicle. The completed hydrodynamic model will be validated in the water tank. Due to the limitation of the time of the testing, only the heave and yaw direction were validated with the numerical simulation. Nevertheless, there is no single paper published on identifying the hydrodynamic parameters of a complex–shaped ROV using both STAR CCM+™ and WAMIT™ then MATLAB™ for virtual reality simulation in 3D.

The paper is organized as follows. Section 2 gives an overview of the dynamic model of the ROV. It is followed by the hydrodynamic damping and added mass modeling and validation in Sects. 3 and 4, respectively. Sections 5 and 6 discuss the experimental results conducted in the water tank and virtual simulation of ROV model, respectively. Lastly, Sect. 7 concludes the paper with future works.

2 Numerical ROV modelling

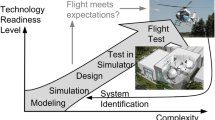
In the proposed ROV modeling approach, Fig. 1 shows the overall approach from numerical modeling to control system design. The computer-aided design (CAD) model of an ROV will be created using software such as SolidWorks™ and MultiSurf™. With the CAD model obtained, the hydrodynamic parameters like hydrodynamic damping and added mass coefficients for the nonlinear ROV model are determined using WAMIT™ and MATLAB™. The obtained ROV model is later validated experimentally for virtual reality simulation in Simulink™.

Fig. 1
figure 1

Overall flow chart of proposed systematic computation of ROV model for virtual reality

Full size image

Figure 2 shows the geometrical model of the ROV modeled by Solidworks™ [24]. The ROV is actuated by six DC brushless thrusters (T1 to T6) for the surge, sway, heave, roll, pitch, and yaw. The mechanical properties such as mass, a moment of inertia, the center of gravity and buoyancy of the ROV are obtained. In Fig. 2, the ROV has a mass of approximately 75 kg in the air with an overall dimension of 1455 mm (length) × 950 mm (width) × 400 mm (height).

Fig. 2
figure 2

CAD SolidWorks™ model for ROV and its body-fixed coordinate system

Full size image

The derivation of ROV dynamic equation is based on following assumptions to simplify the ROV model.

  • Operating at slow speed (less than 1 m/s);

  • Rigid body and fully submerged in water (no wave and current disturbance);

  • Neutrally buoyant by design;

  • Tether (or umbilical cable) dynamics attached to ROV is not considered.

The notations (see Table 1) used for the ROV motions follow the Society of Naval Architects and Marine Engineers (SNAME).

Table 1 Notations used for ROV
Full size table

The Newtonian mechanics are the most common approach to model the rigid body ROV on its body-fixed reference frame [1]. It can be written as follows.

$${\mathbf{M}}_{{{\mathbf{RB}}}} {\dot{\mathbf{v}}} + {\mathbf{C}}_{{{\mathbf{RB}}}} {\mathbf{(v}}) = {\varvec{\uptau}}_{{{\mathbf{RB}}}} ,$$
(1)

where \({\mathbf{M}}_{{{\mathbf{RB}}}} \in \Re^{6 \times 6}\) is the mass matrix, \({\mathbf{C}}_{{{\mathbf{RB}}}} ({\mathbf{v}} )\in \Re^{6 \times 6}\) is the Coriolis and centripetal matrix, \({\varvec{\uptau}}_{{{\mathbf{RB}}}} \in \Re^{6}\) is a vector of external forces and moments, \({\mathbf{v}} = \left[ {\begin{array}{*{20}c} u & v & w & p & q & r \\ \end{array} } \right]^{\text{T}} \in \Re^{6}\) is the linear and angular velocity vector.

According to Fossen [1], the mass inertia matrix in (1) can be written as:

$${\mathbf{M}}_{{{\mathbf{RB}}}} = \left[ {\begin{array}{*{20}c} m & 0 & 0 & 0 & {mz_{G} } & { - my_{G} } \\ 0 & m & 0 & { - mz_{G} } & 0 & {mx_{G} } \\ 0 & 0 & m & {my_{G} } & { - mx_{G} } & 0 \\ 0 & { - mz_{G} } & {my_{G} } & {I_{x} } & { - I_{xy} } & { - I_{xz} } \\ {mz_{G} } & 0 & { - mx_{G} } & { - I_{yx} } & {I_{y} } & { - I_{yz} } \\ { - my_{G} } & {mx_{G} } & 0 & { - I_{zx} } & { - I_{zy} } & {I_{z} } \\ \end{array} } \right],$$
(2)

where the component m in this matrix represents the mass of the vehicle (where I x , I y , I z  I xy , I xz , I yz represent the mass moments of inertia of ROV). x G , y G and z G are the coordinates of the center of gravity of ROV.

The Coriolis and the centripetal matrix are used to describe the angular motion of the vehicle as follows.

$${\mathbf{C}}_{{{\mathbf{RB}}}} ({\mathbf{v}}) = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{ 3\times 3} } & {{\mathbf{C}}_{{{\mathbf{12}}}} ({\mathbf{v}})} \\ { - {\mathbf{C}}_{{{\mathbf{12}}}}^{\text{T}} ({\mathbf{v}})} & {{\mathbf{C}}_{{{\mathbf{22}}}} ({\mathbf{v}})} \\ \end{array} } \right]$$
(3)

and

$${\mathbf{C}}_{{{\mathbf{12}}}} ({\mathbf{v}}) = \left[ {\begin{array}{*{20}c} {m(y_{G} q + z_{G} r)} & { - m(x_{G} q - w)} & { - m(x_{G} r + v)} \\ { - m(y_{G} p + w)} & {m(z_{G} r + x_{G} p)} & { - m(y_{G} r - u)} \\ { - m(z_{G} p - v)} & { - m(z_{G} q + u)} & {m(x_{G} p + y_{G} q)} \\ \end{array} } \right]$$
(4)
$${\mathbf{C}}_{{{\mathbf{22}}}} ({\mathbf{v}}) = \left[ {\begin{array}{*{20}c} 0 & { - I_{yz} q - I_{xz} p + I_{z} r} & {I_{yz} r + I_{xy} p - I_{y} q} \\ {I_{yz} q + I_{xz} p - I_{z} r} & 0 & { - I_{xz} r - I_{xy} q + I_{x} p} \\ { - I_{yz} r - I_{xy} p + I_{y} q} & {I_{xz} r + I_{xy} q - I_{x} p} & 0 \\ \end{array} } \right]$$
(5)

As shown in Eq. 1, the \({\varvec{\uptau}}_{{{\mathbf{RB}}}}\) includes three different hydrodynamics forces and moments. The first term consists of drag, added mass and restoring forces that named as \({\varvec{\uptau}}_{{\mathbf{H}}}\) and the propulsion forces generated by the thrusters are named as \({\varvec{\uptau}}\).

$${\varvec{\uptau}}_{{{\mathbf{RB}}}} = {\varvec{\uptau}}_{{\mathbf{H}}} + {\varvec{\uptau}}$$
(6)

In this paper, the hydrodynamic forces and moments \({\varvec{\uptau}}_{{\mathbf{H}}}\) are determined. These hydrodynamics forces and moments are represented by following equation:

$${\varvec{\uptau}}_{{\mathbf{H}}} = - {\mathbf{M}}_{{\mathbf{A}}} {\dot{\mathbf{v}}} - {\mathbf{C}}_{{\mathbf{A}}} {\mathbf{(v)v}} - {\mathbf{D}}({\mathbf{v}}) - {\mathbf{g(\eta }})$$
(7)

By substituting (7) into (6) and back into (1), the following equation of motions for the ROV is formed.

$${\mathbf{M\dot{v}}} + {\mathbf{C}}({\mathbf{v}}){\mathbf{v}} + {\mathbf{D}}\left( {\mathbf{v}} \right) + {\mathbf{g}}({\varvec{\upeta}}) = {\varvec{\uptau}},$$
(8)

where \({\mathbf{v}} = \left[ {\begin{array}{*{20}c} u & v & w & p & q & r \\ \end{array} } \right]^{\text{T}}\) is the body-fixed velocity vector, and \({\varvec{\upeta}} = \left[ {\begin{array}{*{20}c} x & y & z & \varphi & \theta & \psi \\ \end{array} } \right]^{\text{T}}\) is the earth-fixed vector comprising the position vector. \({\mathbf{M}} = {\mathbf{M}}_{{{\mathbf{RB}}}} + {\mathbf{M}}_{{\mathbf{A}}} \in \Re^{6 \times 6}\) is the inertia matrix for rigid body and added mass, respectively, The gravitational and buoyancy vector acting on ROV in water is denoted by \({\mathbf{g}}({\varvec{\upeta}})\) [1]. Since the ROV is neutrally buoyant (\({\text{W}} = {\text{B}}\)) and the X–Y coordinates of the C.B. coincide with the X–Y coordinate of the CG (by placing additional mass on ROV). Since \((z_{G} - z_{B} ) = -0.397\,{\rm m}\), the resulting \({\mathbf{g}}({\varvec{\upeta}})\) can be expressed as \({\mathbf{g}}({\varvec{\upeta}}) = \left[ {0 \, 0 \, 0{ - 0} . 3 9 7 {\text{W}}\cos \theta \sin \varphi { - 0} . 3 9 7 {\text{W}}\sin \theta \, 0} \right]^{\text{T}}\). The Coriolis and centripetal matrix for rigid body and added mass can be defined as: \({\mathbf{C}}({\mathbf{v}})\) \(= {\mathbf{C}}_{{{\mathbf{RB}}}} ({\mathbf{v}}) + {\mathbf{C}}_{{\mathbf{A}}} ({\mathbf{v}}) \in \Re^{6 \times 6}\), \({\mathbf{D}}\left( {\mathbf{v}} \right) \in \Re^{6 \times 6}\) is the damping matrix due to the surrounding fluid. The input force and moment vector \({\varvec{\uptau}} = {\mathbf{Tu}} \in \Re^{6}\) relate the thrust output vector \({\mathbf{u}}\) with the thruster configuration matrix \({\mathbf{T}}\). As observed in the design of ROV, it is a fully actuated system with six thrusters. The thruster configuration matrix \({\mathbf{T}}\) based on the layout of the thrusters in ROV platform is defined as follows.

$${\mathbf{T}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {\cos \alpha } & {\cos \alpha } \\ { - \cos \beta } & {\cos \beta } & 0 & 0 & {\sin \alpha } & { - \sin \alpha } \\ {\cos \beta } & {\cos \beta } & 1 & 1 & 0 & 0 \\ { 0. 1 5 5 {\text{cos}}\beta } & { - 0. 1 5 5\cos \beta } & { - 0.275} & {0.275} & 0 & 0\\ { 0. 3 9 4 {\text{cos}}\beta } & { 0. 3 9 4 {\text{cos}}\beta } & {{ - 0} . 0 3 5} & {{ - 0} . 0 3 5} & { 0. 4 3 0 {\text{cos}}\beta } & { 0. 4 3 0 {\text{cos}}\beta } \\ {{ - 0} . 3 9 4 {\text{sin}}\beta } & { 0. 3 9 4\sin \beta } & { 0} & 0& { - { 0} . 6 6 0 {\text{sin}}\beta } & {{ 0} . 6 6 0 {\text{sin}}\beta } \\ \end{array} } \right],$$
(9)

where \(\alpha = 45^{\text{o}}\) is the inclination angle for T5 and T6 while \(\beta = 45^{\text{o}}\) is the orientation angle for T1 and T2. Note that T3 and T4 are the two vertical thrusters shown in Fig. 2. The computation of hydrodynamic added mass and damping coefficients are discussed in Sects. 3 and 4.

3 Hydrodynamic damping model

The hydrodynamic damping coefficients of the ROV are computed in the report [24]. The vehicle has a mass of 75 kg, volume of 0.05 m3 and surface area of 4.75 m2. The moment of inertia of ROV is shown in Table 2.

Table 2 Moment of inertia properties of ROV [24]
Full size table

As a result, the rigid body ROV mass inertia in (1) can be written as:

$${\mathbf{M}}_{{{\mathbf{RB}}}} = \left[ {\begin{array}{*{20}c} {75.00} & 0 & 0 & 0 & 0 & 0 \\ 0 & {75.00} & 0 & 0 & 0 & 0 \\ 0 & 0 & {75.00} & 0 & 0 & 0 \\ 0 & 0 & 0 & {2.51} & 0 & 0 \\ 0 & 0 & 0 & 0 & {3.38} & {0.01} \\ 0 & 0 & 0 & 0 & {0.01} & {1.73} \\ \end{array} } \right]$$
(10)

A submerged body experiences lift and drag effect while moving through the fluid. This drag component includes frictional and pressure drag. The frictional drag due to the boundary layers depends on the surface area in contact with the fluid. The damping function is a linear function of velocity, a quadratic function of velocity, a sum of both linear and quadratic terms (as used in this paper) and with higher order forms. The steady drag force experienced by the vehicle in its reference state is well known to depend on the square of the velocity and a coefficient that depends on Reynolds number (for a body sufficiently submerged in a fluid). The variation of that force on the body experienced during small perturbations to that motion has repeatedly been found to be better modeled by a linear function of velocity. The linear coefficients are therefore adequate to represent the strength and moments due to inviscid part of the flow for a low-speed ROV.

The ROV hydrodynamic damping matrix D can be further simplified. The off-diagonal elements [1] in the hydrodynamic damping matrix D(v) are small compared to those diagonal elements on the underwater vehicle. Therefore, D(v) becomes a diagonal matrix: \({\text{diag}}\left[ {\left\{ {X_{u} ,Y_{v} ,Z_{w} ,K_{p} ,M_{q} ,N_{r} } \right\}} \right].\) A turbulence model with the unsteady 3-dimensional flow was built for the Reynolds number flow condition greater than 1.0 × 106. The Shear Stress Transport (SST) model in CFD software STAR CCM+ was used. The k-ω SST model is one of the two common models for predicting the flow separation under adverse pressure gradient. It provides a highly accurate prediction of the amount of the flow separation under adverse eddy-viscosity. To take advantage of the SST model, the boundary layer should be resolved with at least 10 mesh nodes. This is done by inspecting the y+ value on the surface of the ROV that must be around one.

The movement in the fluid domain is expected to be turbulent and isothermal. The temperature is fixed at 20 °C and the water is modeled as an incompressible fluid. It is impractical to set the fluid domain to be infinitely large to analyze damping force acting on ROV in CFD. As a result, a dimension of approximately 15 times greater than the dimension of the ROV (see Fig. 3) to ensure the accuracy [5] of the actual flow domain is used. The properties of the flow domain are required to be defined to ensure the domain has the high fidelity. The turbulence properties are difficult to define without turbulent kinetic energy and dissipation data at the inlet flow. The turbulent intensity was used to describe the turbulent properties in the simulation. The turbulent intensity is selected to be 0.1% for the external flow over the vehicle. The static pressure is used at outlet boundary. It is required to use the log-law method to predict the velocity profile in the turbulent wall-bounded flows. The side, top, and bottom of the fluid domain are modeled using free slip wall boundary conditions. The boundary condition of the ROV surface is defined to be non-slip due to fluid viscosity, and the surface speed of the ROV is near to zero.

Fig. 3
figure 3

3D view of volumetric meshing for flow domain (top) and close view of ROV (bottom)

Full size image

The initial variable values are required for STAR CCM+™ solver to commence the steady-state calculation. The appropriate settings of the solver control are essential to facilitate the convergence of the simulation results. The selection of appropriate time step size helps to obtain good convergence rates in STAR CCM+ solver. The convergence is achieved by using the physical time steps which provide sufficient relaxation of the non-linearity. A reasonable estimation of this time step is based on one third of the fluid domain length (L) and initial velocity (U). Therefore, \(t = \frac{L}{3U} = \frac{15}{3*1} = 5s\). Table 3 shows the initial and solver control settings.

Table 3 Initial condition and solver control settings [24]
Full size table

Before performing the CFD, the mesh size needs to be defined properly as the shape of the boundary is important in creating pressure gradients which greatly influence the boundary layer. The mesh size is preferred to be sufficiently small to capture the geometry of the ROV. The flow near boundary layer flow can be captured using the layer inflation technique. A surface wrapping technique was used for geometry preparation before the surface meshes to ensure mesh error is kept minimal to improve the meshing quality.

The number of elements in the volume is approximately 2,069,270. The fluid domain has around 546,712 elements. Figure 3 shows the 3D of the volumetric mesh of the flow domain around the ROV. The mesh downstream of the body is finer in the wake region than near the domain boundary.

Different configurations can be computed with a single set of grids. The grid quality will not be affected by changing of ROV’s orientation. It allows different principle motions of the ROV to be simulated with the same flow direction (negative x-axis) in the domain. However, the direction of gravity has to be changed in different principle motion simulation. Table 4 shows the mesh statics and settings used in the simulation.

Table 4 Mesh settings [24]
Full size table

Figure 4 illustrates the flow around the vehicle in four DOFs. The formation of the wake at the rear creates a low-pressure region. The high-pressure region at the front resists the motion of the vehicle. As observed, there is certainly flow separation on the ROV. Figure 5 illustrates the drag force exerting on the ROV and its corresponding drag coefficient. It shows that the drag forces converge to a steady-state value at around 40 iterations.

Fig. 4
figure 4

Vector plot of ROV in STAR CCM+ [24]

Full size image
Fig. 5
figure 5

Iteration history of drag force and its coefficient [24]

Full size image

As observed in Fig. 4, the wakes are formed at the rear of the ROV body when the turbulent flow past the vehicle. The wakes represent the increased in the vortices of the flow separation. The non-linear damping effects on the ROV are caused by this flow separation phenomenon in the turbulent model. The hydrodynamic damping forces were then determined by integrating the pressure on ROV surface. The three translation motions namely: surge, sway, and heave are plotted against the velocity in Fig. 6. As observed from the plots, the vehicle has the largest drag in the heave direction due to its largest frontal area normal to the flow direction of about 0.6 m2. The drag force in sway is slightly larger than the drag in surge direction due to its small frontal area. The damping coefficient for different direction is obtained using second-order polynomial fit as shown in Figs. 6 and 7.

Fig. 6
figure 6

Drag force as the function of velocity in surge, sway, and heave [24]

Full size image
Fig. 7
figure 7

Drag torque as the function of velocity in yaw [24]

Full size image

Table 5 shows the resulted drag coefficient of ROV in its four principle motions. The flow in the domain was simulated at different speeds using STAR CCM+. Table 6 tabulates the drag moment versus angular velocity in the yaw direction.

Table 5 Damping coefficients of ROV in four principle directions [24]
Full size table
Table 6 Drag moment versus angular velocity in yaw direction [24]
Full size table

Figure 7 depicts the drag moment as a function of square angular velocity. The linear damping in yaw direction is ignored as only quadratic damping is present. The resulted hydrodynamic damping for the ROV is, thus, written as:

$${\mathbf{D}}_{{\mathbf{L}}} = - {\text{diag}}\{ [\begin{array}{*{20}c} {3.221} & {3.291} & {5.682} & {0.} & 0 & 0 \\ \end{array} ]\}$$
(11)
$${\mathbf{D}}_{{\mathbf{Q}}} = - {\text{diag }}\{ [\begin{array}{*{20}c} {105.300} & {139.600} & {273.800} & 0 & 0 & {6.079} \\ \end{array} ]\}$$
(12)

In summary, the results show that the lowest damping occurs in surge direction while the heave motion has the largest drag force due to its larger surface area in contact with water. The values of the linear damping coefficients are smaller than the nonlinear damping terms due to its square velocity term.

4 Hydrodynamic added mass model

The hydrodynamic added coefficients of the ROV are now analyzed in the report [24]. The added mass and inertia are independent of the circular wave frequency for a fully submerged vehicle. The added mass coefficients matrix for an ROV can be written as follow:

$${\text{M}}_{\text{A}} = \left[ {\begin{array}{*{20}c} {X_{{\dot{u}}} } & {X_{{\dot{v}}} } & {X_{{\dot{w}}} } & {X_{{\dot{p}}} } & {X_{{\dot{q}}} } & {X_{{\dot{r}}} } \\ {Y_{{\dot{u}}} } & {Y_{{\dot{v}}} } & {Y_{{\dot{w}}} } & {Y_{{\dot{p}}} } & {Y_{{\dot{q}}} } & {Y_{{\dot{r}}} } \\ {Z_{{\dot{u}}} } & {Z_{{\dot{v}}} } & {Z_{{\dot{w}}} } & {Z_{{\dot{p}}} } & {Z_{{\dot{q}}} } & {Z_{{\dot{r}}} } \\ {K_{{\dot{u}}} } & {K_{{\dot{v}}} } & {K_{{\dot{w}}} } & {K_{{\dot{p}}} } & {K_{{\dot{q}}} } & {K_{{\dot{r}}} } \\ {M_{{\dot{u}}} } & {M_{{\dot{v}}} } & {M_{{\dot{w}}} } & {M_{{\dot{p}}} } & {M_{{\dot{q}}} } & {M_{{\dot{r}}} } \\ {N_{{\dot{u}}} } & {N_{{\dot{v}}} } & {N_{{\dot{w}}} } & {N_{{\dot{p}}} } & {N_{{\dot{q}}} } & {N_{{\dot{r}}} } \\ \end{array} } \right],$$
(13)

where \(X_{{\dot{u}}}\) is the added mass along x-axis due to an acceleration in x-direction, \(Y_{{\dot{v}}}\) is the added mass along y-axis due to an acceleration \(\dot{v}\) in the y-direction. On the other hand, the corresponding added Coriolis and centripetal matrix are represented as follow:

$${\text{C}}_{\text{A}} ( {\text{v) = }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & { - a_{3} } & {a_{2} } \\ 0 & 0 & 0 & {a_{3} } & 0 & {-a_{1} } \\ 0 & 0 & 0 & {-a_{2} } & {a_{1} } & 0 \\ 0 & { - a_{3} } & {a_{2} } & 0 & { - b_{3} } & {b_{2} } \\ {a_{3} } & 0 & { - a_{1} } & {b_{3} } & 0 & { - b_{1} } \\ { - a_{2} } & {a_{1} } & 0 & { - b_{2} } & {b_{1} } & 0 \\ \end{array} } \right],$$
(14)

where the respective elements in the matrix are written as follows.

$$\begin{aligned} a_{1} = X_{{\dot{u}}} u + X_{{\dot{v}}} v + X_{{\dot{w}}} w + X_{{\dot{p}}} p + X_{{\dot{q}}} q + X_{{\dot{r}}} r \hfill \\ a_{2} = X_{{\dot{v}}} u + Y_{{\dot{v}}} v + Y_{{\dot{w}}} w + Y_{{\dot{p}}} p + Y_{{\dot{q}}} q + Y_{{\dot{r}}} r \hfill \\ a_{3} = X_{{\dot{u}}} u + Y_{{\dot{v}}} v + Z_{{\dot{w}}} w + Z_{{\dot{p}}} p + Z_{{\dot{q}}} q + Z_{{\dot{r}}} r \hfill \\ b_{1} = X_{{\dot{u}}} u + Y_{{\dot{v}}} v + Z_{{\dot{w}}} w + K_{{\dot{p}}} p + K_{{\dot{q}}} q + K_{{\dot{r}}} r \hfill \\ b_{2} = X_{{\dot{u}}} u + Y_{{\dot{v}}} v + Z_{{\dot{w}}} w + K_{{\dot{p}}} p + M_{{\dot{q}}} q + M_{{\dot{r}}} r \hfill \\ b_{3} = X_{{\dot{u}}} u + Y_{{\dot{v}}} v + Z_{{\dot{w}}} w + K_{{\dot{p}}} p + M_{{\dot{q}}} q + N_{{\dot{r}}} r \hfill \\ \end{aligned}$$
(15)

The surface-based computer-aided design (CAD) software MULTISURF™ modeled the geometry of the ROV. The software MULTISURF™ aims to work with WAMIT™ for exporting the necessary files for analysis. The ROV is made of multi-bodies that can be created using MULTISURF™ and later use WAMIT™ to compute the added mass matrix as shown below.

The geometry file was imported to WAMIT™ by MATLAB™. The widely used low-order panel method was adopted in WAMIT™. The output file created can be imported into MATLAB™ to obtain the hydrodynamic added mass. Figure 8 illustrates the procedure for computing the hydrodynamic added mass coefficients.

Fig. 8
figure 8

Program flowchart for computing added mass coefficients [13]

Full size image

Table 7 shows the descriptions of each file (see Fig. 8) used in determining the added mass coefficients. All the necessary parameters required are shown in the following input files. Before using the WAMIT™ to test the ROV, a study on the empirical results of a 2 m diameter sphere (see Fig. 9) was used to verify the program setup and parameters. In Table 8, the theoretically added mass of a sphere is \(A = 2/3\pi \rho r^{3}\) for the three translational motion; surge, sway and, heave. The added mass of the sphere can be written as \(A = 2/3\pi r^{3}\)(after normalizing with density). Table 8 shows the low-order method results of the sphere are quite close to the theoretical value of 2.094.

Table 7 Description of records used in WAMIT™ solver
Full size table
Fig. 9
figure 9

Finite surface panels generation of sphere using MULTISURF™

Full size image
Table 8 Low-order method for sphere [24]
Full size table

Additionally, it is required to define the depth of the submerged body in WAMIT™. The impact of different water depth has been identified by the same sphere. As shown in Table 9, the results of the added mass converged at approximately 10 m. As a result, the computation will be performed at 10 m.

Table 9 Added mass of sphere at different depth [24]
Full size table

The numerical results obtained from WAMIT™ low-order method have a small difference compared with the theoretical results. Nevertheless, it helps to ensure that the input parameters settings used are appropriate to calculate the added mass coefficient of the ROV. The ROV modeled using MULTISURF™ is then imported into the WAMIT™ to solve the problem using the low-order panel method. As shown in Fig. 10, the main components of the ROV are drawn to reduce the complexity of the geometry.

Fig. 10
figure 10

ROV model from WAMIT™

Full size image

Figures 11 and 12 show the added mass coefficient components calculated by WAMIT™. The convergence tests of the added mass for different panel numbers converged in approximately 3000–4000 panels. It shows that the minimum required panel numbers should be at least 3000.

Fig. 11
figure 11

Convergence plot for surge, sway and heave direction [24, 25]

Full size image
Fig. 12
figure 12

Convergence plot for roll, pitch, and yaw direction [24, 25]

Full size image

The off-diagonal terms of the added mass are less than the diagonal components as the ROV has near to three planes of symmetry [1]. Hence, the added mass matrix obtained can be further simplified.

$${\mathbf{M}}_{{\mathbf{A}}} = - \left[ {\begin{array}{*{20}c} {20.392} & 0 & 0 & 0 & 0 & 0 \\ 0 & {53.435} & 0 & 0 & 0 & 0 \\ 0 & 0 & {126.144} & 0 & 0 & 0 \\ 0 & 0 & 0 & {2.802} & 0 & 0 \\ 0 & 0 & 0 & 0 & {13.703} & 0 \\ 0 & 0 & 0 & 0 & 0 & {5.263} \\ \end{array} } \right]$$
(16)

The added mass matrix \({\mathbf{M}}_{{{\mathbf{A}} }}\) of the ROV must be positive. The following relations are observed from the matrix: \(m_{11} < m_{22} < m_{33}\). A smaller added mass in surge direction, i.e., m 11 has been observed. It is due to the ROV has the smallest projection area in surge direction. The corresponding coriolis and centripetal added mass matrix in (14) can be rewritten:

$${\text{C}}_{\text{A}} ( {\text{v) = }}\left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & { - 126.144w} & {53.435v} \\ 0 & 0 & 0 & {126.144w} & 0 & { - 20.392u} \\ 0 & 0 & 0 & { - 53.435v} & {20.392u} & 0 \\ 0 & { - 126.144w} & {53.435v} & 0 & { - 5.263r} & {13.703q} \\ {126.144w} & 0 & { - 20.392u} & {5.263r} & 0 & { - 2.802p} \\ { - 53.435v} & {20.392u} & 0 & { - 13.703q} & {2.802p} & 0 \\ \end{array} } \right]$$
(17)

In summary, the added mass coefficients of the ROV are around 20 kg in surge direction, 53 kg in sway direction and followed by 126 kg in heave direction. The ROV has the larger added mass in heave, followed by sway and surge direction. In summary, the computations of the hydrodynamic damping and added mass were performed. The proposed numerical simulation can determine the hydrodynamic parameters.

5 Validation using experimental results

The results obtained from the simulations were validated with the experimental data [25] in a water tank. The heave and yaw motion were only validated due to the limited reliable sensor installed on the ROV. A depth sensor, Doppler Velocity Log (DVL) and Inertial Measurement Unit (IMU) were jointly used to measure the depth, velocity, and acceleration of the ROV, respectively. The water tank dimensions are: 10 m (L) × 4 m (W) × 1.8 m (D). It is equipped with an overhead crane to load and unload the ROV. The sample rate of 100 Hz (or sample period of 0.01 s) was used to sample the raw data from the sensor. The raw data are plotted against the sample count using a MATLAB script. Note that one sample count is equivalent to 0.01 s.

5.1 Heave model identification

During the depth validation, the prototype ROV (see Fig. 13) was maintained at a fixed heading angle before submerging to a depth of 1 m as shown in Fig. 13. The ROV was commanded to move vertically into the water with little acceleration measured by IMU. The dead-reckoning data for acceleration in Z-direction is not zero as shown in Fig. 14. The ROV is not moving at constant heave rate as observed in the heave velocity from the DVL in Fig. 15. The thrust outputs from T3 and T4 (for heave direction) are approximately 10 N (see Fig. 16) to allow the ROV to reach to a depth of 1 m as depicted in Fig. 17.

Fig. 13
figure 13

Image of ROV's motion pictures captured during heave test in water

Full size image
Fig. 14
figure 14

Acceleration in heave direction (1 sample count = 0.01 s)

Full size image
Fig. 15
figure 15

Heave velocity response (1 sample count = 0.01 s)

Full size image
Fig. 16
figure 16

Thrust output from thruster T3 or T4 (1 sample count = 0.01 s)

Full size image
Fig. 17
figure 17

Depth response (1 sample count = 0.01 s)

Full size image

The added mass \(Z_{{\dot{w}}}\) and damping coefficients (linear, Z w ) due to the hydrodynamic force are defined in a body-fixed frame with m is the body mass of the ROV. The heave model can be simplified:

$$(m + Z_{{\dot{w}}} )\dot{w} + Z_{w} w = Z$$
(18)

The ROV is designed to be neutrally buoyant, and the centripetal and Coriolis terms are not present in the equation as the ROV was commanded to move in heave direction only. Rearranging the preceding equation gives:

$$\dot{w} = \frac{Z}{{\left( {m + Z_{{\dot{w}}} } \right)}} - \frac{{Z_{w} }}{{\left( {m + Z_{{\dot{w}}} } \right)}}w.$$
(19)

In matrix form,

$$\overbrace {{\dot{w}}}^{{\mathbf{\varphi }}} = \overbrace {{\left[ {\begin{array}{*{20}c} Z & { - w} \\ \end{array} } \right]}}^{{\mathbf{H}}} \, \overbrace {{\left[ {\begin{array}{*{20}c} \alpha \\ \beta \\ \end{array} } \right]}}^{{{\hat{\mathbf{\theta }}}}},$$
(20)

where

$$\alpha = \frac{1}{{\left( {m + Z_{{\dot{w}}} } \right)}};\beta = - \frac{{Z_{w} }}{{\left( {m + Z_{{\dot{w}}} } \right)}} \,$$
(21)

The least square method below is used to obtain the estimated values.

$$\underbrace {{\left[ {\begin{array}{*{20}c} {\dot{w}_{1} } \\ {\dot{w}_{2} } \\ \vdots \\ \end{array} } \right]}}_{{\mathbf{\varphi }}} = \underbrace {{\left[ {\begin{array}{*{20}c} {Z_{1} } & { - w_{1} } \\ {Z_{2} } & { - w_{2} } \\ \vdots & \vdots \\ \end{array} } \right]}}_{{\mathbf{H}}} \cdot \underbrace {{\left[ {\begin{array}{*{20}c} \alpha \\ \beta \\ \end{array} } \right]}}_{{\varvec{\uptheta}}} +\, {\text{error,}}$$
(22)

where subscript i represents the number of samples collected from the experiment. The standard least square solution is given by the Moore–Penrose pseudo inverse:

$${\hat{\mathbf{\theta }}}_{{{\mathbf{LS}}}} = {\mathbf{(H}}^{{\mathbf{T}}} {\mathbf{H)}}^{{ - {\mathbf{1}}}} \cdot {\mathbf{H}}^{{\mathbf{T}}} \cdot {\mathbf{\varphi }},$$
(23)

where the standard deviation, \(\text{cov} ({\hat{\mathbf{\theta }}}_{{{\mathbf{LS}}}} ) = \sigma^{2} ({\mathbf{H}}^{{\mathbf{T}}} {\mathbf{H}})^{ - 1}\) and note that \({\mathbf{H}}\) has to be a full rank matrix. The recursive least square (RLS) is used to compute the parameters \({\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} \, (t)\) in (23). The parameters update \({\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} \, (t)\) includes a correction term to the previous estimate \({\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} \, (t{ - 1})\) as seen in (24). The typical RLS algorithm comprises the following recursive equations computed in sequence. For example, \({\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} \, (t{ - 1})\) in (24) requires the computation of (25)–(27).

$${\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} (t) = \, {\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} (t{ - 1}) + {\mathbf{K}}(t)\varepsilon (t)$$
(24)
$${\varvec{\upvarepsilon}}(t) = \, {\dot{\mathbf{w}}} (t) - {\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}}^{{\mathbf{T}}} (t - 1){\mathbf{H}}(t)$$
(25)
$${\mathbf{K}}(t) = \, \frac{{\lambda^{ - 1} {\mathbf{P}} (t{ - 1)}{\mathbf{H}} ( {\text{t)}}}}{{1 + \lambda^{ - 1} {\mathbf{H}}^{\text{T}} {\mathbf{P}}(t - 1){\mathbf{H}}(t)}}$$
(26)
$${\mathbf{P}}(t) = \, \lambda^{ - 1} {\mathbf{P}} (t{ - 1) - }\lambda^{ - 1} {\mathbf{K}}^{\text{T}} (t ){\mathbf{H}} (t ){\mathbf{P}} (t{ - 1)}$$
(27)

The above equations need an initial value for \({\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} \, (t)\) and the error covariance matrix \({\mathbf{P}}\). The initial value of \({\hat{\mathbf{\theta }}}_{{{\mathbf{RLS}}}} \, (t)\) is set as 0 and \({\mathbf{P}}\) is 100I 2 where I 2- is the identity matrix of dimension two. The forgetting factor that specifies how fast the RLS forget the past sample information is set to 0.001. For example, using λ = 1, it specifies an infinite memory. By comparing the RLS with a different forgetting factor, the following plot in Fig. 18 is obtained. In Fig. 18, the RLS with a lower forgetting factor has a closer behavior to the measured data. In general, it can be observed that the differences in the performance are quite large for the damping in the heave direction as seen in Table 10. It may be due to the effect of the rotating propeller of the thrusters are not included during the simulation.

Fig. 18
figure 18

Comparison of heave velocity response using RLS

Full size image
Table 10 Comparisons between simulation and experimental results in heave direction
Full size table

5.2 Yaw model identification

A simplified description of the yaw model of the ROV is defined as

$$N_{{\dot{r}}} \dot{r} + N_{\left| r \right|r} \left| r \right|r + N_{r} r = N,$$
(28)
$$\dot{\psi } = r,$$
(29)

where \(N_{{\dot{r}}}\) is the added inertia \(( = I_{r} + N_{{\dot{r}}} )\) in yaw direction. \(N_{r}\) is the linear component of drag force in the yaw direction and \(N_{\left| r \right|r}\) is the quadratic component of drag force in the yaw direction. \(r\) is the heading velocity, \(\dot{r}\) is the heading acceleration, \(N\) is the moment input to the ROV due to the thrusters (T1, T2, T5, and T6) and \(\psi\) is the heading angle. The constant heading velocity refers to \(\dot{r}\) heading acceleration equal to 0, the yaw equation of motion becomes:

$$N_{\left| r \right|r} \left| r \right|r + N_{r} r = N$$
(30)

The test was performed to estimate the drag coefficients \(N_{\left| r \right|r}\) and \(N_{r}\) in the heading equation. A fixed velocity commands are sent to the four thrusters T1 T2 T5 and T6 and the steady-state heading velocity responses were recorded using the DVL sensor. The moment in yaw direction was computed using the thrusts generated by the thrusters multiplied by the moment arm (i.e., distance) from the centre of gravity. Figure 19 gives the steady-state angular velocity as a result of the input command to the thrusters (1.3–2.7 V). The plot of the moment vs. the angular velocity is shown in Fig. 20 where the linear and quadratic damping terms can be determined from the curve fitting. The value of \(N_{\left| r \right|r}\) and \(N_{r}\) are estimated as 5.4815 and 4.6114, respectively.

Fig. 19
figure 19

Velocity profile at constant control command to thruster T1, T2, T5 and T6

Full size image
Fig. 20
figure 20

Angular velocity rate versus moment in yaw direction

Full size image

The added mass of the ROV in the yaw direction is then identified as shown. A sinusoidal control command (maximum torque corresponding to the heading velocity) is applied to the thruster T1 T2 T5 and T6 of the ROV. A sinusoidal control signal with 10 Hz frequency is applied to the thrusters with a value corresponding to +2.7 V to −2.7 V (for both forward and reverse direction).

As observed in Fig. 21 and 22, the maximum heading velocity is observed to be approximately 0.385 rad/s. With 2.7 V control signal into the thruster, the constant heading velocity is approximately 0.435 rad/s that corresponds to 31.52 Nm to achieve a heading speed of 0.435 rad/s. However, the maximum sinusoidal angular speed is around 0.385 rad/s. As the measured heading velocity is smaller than the speed measured in the water tank test, it shows that the ROV needs addition moment to overcome the resistance due to its body mass and the added mass. If the amplitude of the sine input is increased to around 0.435 rad/s, +2.9 V to −2.9 V sine control signal (see Fig. 23) has a torque approximately 35.17 Nm. It indicates that the ROV needs an additional of 35.17 − 31.52 = 3.65 Nm to overcome both the body inertia and added mass during the motion.

Fig. 21
figure 21

Heading velocity response subjected by sine signal command input (2.7 V) for thruster T1, T2,T5 and T6

Full size image
Fig. 22
figure 22

Heading velocity due to constant control command (2.7 V) for thruster T1, T2,T5 and T6

Full size image
Fig. 23
figure 23

Heading velocity of sine input command of 2.9 V for thruster T1, T2,T5 and T6

Full size image

The next step is to compute the angular acceleration using the +2.9 V to −2.9 V sine control signal. The maximum heading acceleration of approximately 0.85 rad/s2 was measured (see Fig. 24) by Inertial Measurement Unit sensor.

Fig. 24
figure 24

Angular acceleration of sine input signal of 2.9 V

Full size image
$$N_{{\dot{r}}} \dot{r} = \Delta N,$$
(31)

where \(\Delta N\) is the difference at the moment and \(N_{{\dot{r}}}\) is the hydrodynamic added mass in the yaw direction.

The moment due to the body inertia and added mass is computed as follows.

$$N_{{\dot{r}}} \dot{r} = \Delta N = 3 5. 1 6 { - 31} . 5 1 { = 3} . 6 5$$
(32)

Substituting the peak acceleration equals 0.85 rad/s2, \(N_{{\dot{r}}}\) obtained from (31) becomes 4.3 kg.m2. As a result, the heading model can be written as:

$$4.3\dot{r} + 5.4815\left| r \right|r + 4.6114r = N$$
(33)

The results tabulated in Table 11 show that the quadratic damping has a closer value as compared to the experiments. The added mass does not seem to compare well with the simulation result. It may be due to the experimental test setup in a water tank that influences the reading. The effects of the interaction effect between rotating propellers and propeller-to-ROV’s hull have not been included in the simulation.

Table 11 Comparisons between simulation and experimental results in yaw direction
Full size table

6 Simulation of ROV model in virtual reality

The identified ROV parameters from the previous sections are used to model the ROV virtually in MATLAB™/Simulink™ environment. The differential equation of the ROV is solved by ordinary differential equation solver such as Dormand–Prince solver. The six inputs (T1–T6) on the left-hand side are the thruster inputs. For example, the ROV is commanded to move in Z-direction using only T3 and T4 thruster. An ROV simulator developed in MATLAB™/Simulink™ environment is shown in Fig. 25.

Fig. 25
figure 25

Nonlinear ROV model

Full size image

A virtual underwater world environment was developed to enhance the user interface in Fig. 26. A virtual reality world for the ROV uses the output signals from the ROV model to move the ROV virtually. It allows the movement and position data to be animated and displayed during the dynamic positioning. Firstly, the CAD model is exported into Virtual Reality Modelling Language file format for the V-Realm editor to edit the model. The V-Realm Builder has an extensive object library where the user can import the 3D background sceneries and objects to create a virtual world. The backgrounds such as the sea and offshore structures are then imported from the library. The VR-sink block diagram in Simulink™ connects between VRML model and Simulink™ block diagrams.

Fig. 26
figure 26

Virtual reality world of ROV

Full size image

Secondly, the Simulink™ model of the ROV is connected to the virtual world through VR- Sink block. By connecting the model to the virtual world, the output data from the Simulink™ model can be used to control and animate the virtual world as shown in Fig. 26. The translational ROV’s motion outputs and the rotational motion outputs use the Euler’s transformation to animate the position of the ROV in the virtual reality world. Thirdly, the ROV can be controlled by a joystick using the user interface design the Qt GUI in Ubuntu 14 operating system as shown in Fig. 27.

Fig. 27
figure 27

User interface for controlling ROV during test

Full size image

The simulated time response of heave and yaw model of the ROV are compared with experimental result in the water tank are shown in Figs. 28 and 29. Due to the constraints, only the heave and yaw models are verified. During the tests, the ROV was commanded to move to a target depth of 0.3 m and 140° yaw angle. As shown in Fig. 28, the ROV can settle to a steady-state value of 0.3 m via the propulsion force generated by mainly T3 and T4 thruster. The ROV takes around 30 samples to settle to its steady-state value. The difference in the response is due to the thrusters dynamics that are not included in the simulation. As shown in Fig. 29, the ROV can regulate itself at a constant yaw rate with the steady-state yaw angle maintained at 140° for almost 15,000 samples (or 150 s). In summary, the experimental validation demonstrates that the numerical model in heave and yaw models behave reasonably close to the actual ROV responses. Although the numerical error due to the CFD is 28 and 18% for the heave and yaw direction, respectively, it gives a fairly sufficient model for the initial control system design.

Fig. 28
figure 28

Heave response between the simulated and experiment results of ROV

Full size image
Fig. 29
figure 29

Yaw response between the simulated and experiment results of ROV

Full size image

7 Conclusion

A systematic modeling of the hydrodynamic damping and added mass of a complex-shaped remotely operated vehicle using few numerical software was presented. The computational fluid dynamic software STAR CCM+™ was used to determine the damping parameters of the ROV model. Additionally, potential flow code using WAMIT™ was used to predict the added mass on the ROV model obtained from MULTISURF™ using the panel method to solve the potential flow around the vehicle. The simulated results were verified with the experimental tests in the water tank. Due to test constraints, only the results on the heave and yaw direction were shown. The test results show quite a close match in the added mass for the heave direction and quadratic damping coefficient in the yaw direction. However, the remaining coefficients exhibit some errors as seen in the numerical results. Experimental tests were conducted in a water tank using the joystick as a control to move the ROV to certain desired locations in heave and yaw direction. The experimental tests exhibit some trends to the simulated results in the heave and yaw directions. In summary, the proposed method provides a viable alternative with reasonable results at an early design stage where the test facilities and workforce can be quite expensive to justify for a prototype ROV. It also provides a sufficient model and insight to the ROV behavior for better control the ROV instead of relying on “black box” approach of using non-model based artificial neural network.

Future works could improve the accuracy of the CFD results by comparing the numerical simulation with the ROV using real-time adaptive identification approach in sea trial. The rotating propeller modeling will be included to simulate the interaction effect between rotating propellers and propeller–hull interaction. The different control system design using various controllers will be performed.