Relaxation in Pulsed EPR: Thermal Fluctuation of Spin-Hamiltonian Parameters of an Electron-Nuclear Spin-Coupled System in a Malonic Acid Single Crystal in a Strong Harmonic-Oscillator Restoring Potential

Abstract

Random fluctuations in the $\tilde{g}$ and $\tilde{A}$ matrices of a spin system due to thermal motion of a molecule are specifically considered to calculate the relaxation matrix for the four-level electron-nuclear spin-coupled system ($S = 1/2$; $I = 1/2$) in a malonic acid crystal, using the formalism outlined by Lee et al. (J Chem Phys 98:3665–3689, 1993). The correlation time, τ_c, and the value of the parameter λ, characterizing the harmonic-oscillator restoring potential of the small-amplitude fluctuation of the director of the malonic-acid molecule due to thermal motion are estimated from the knowledge of the experimental values of (τ_c, λ). The four electronic, $T_{2e} ,$ and the two nuclear, $T_{{2{\text{n}}}}$, spin relaxation times are calculated to be functions of (τ_c, λ) governing the fluctuations. The values of (τ_c, λ), evaluated with these expressions, when fitted to the experimental values of $T_{2e}$ and $T_{2n}$, assuming the molecule to be in the ground state (n = 0) in the harmonic-oscillator potential, a rather narrow region of (τ_c, λ) values about τ_c = 0.081 μs and $\lambda = 4.4$ is found. These values are then used to calculate the time-dependent echo-ELDOR signal by the relevant Liouville von-Neumann (LVN) equation. The resulting Fourier transform is found to be in excellent agreement with the experimental data. The (τ_c, λ) values for the excited states described by $n = 1,2$ have also been calculated, although these states are unlikely to be populated at room temperature.

Appendices

Appendix A: Spin Hamiltonian

For the specific case of a single nucleus ($I = 1/2$) interacting with an unpaired electron ($S = 1/2$) by hyperfine (HF) interaction, where the HF matrix has the same principal axes as those of the g matrix, the total Hamiltonian is

$$\hat{H} = \hat{H}_{0} + \hat{H}_{1} ,$$

(19)

where

$$\hat{H}_{0} = CS_{z} - \omega_{n} I_{z} + AS_{z} I_{z} + \frac{1}{2}BS_{z} I_{ + } + \frac{1}{2}B^{*} S_{z} I_{ - } .$$

(20)

In Eq. (20) the coefficients are expressed as follows:

$$\begin{gathered} C = \frac{{\beta_{e} B_{0} }}{h}\left[ {\overline{g} + F\frac{1}{2}\left( {3\cos^{2} \beta - 1} \right) + F^{\left( 2 \right)} \sin^{2} \beta \cos \left( {2\gamma } \right)} \right] \hfill \\ A = - 2\pi \left[ {\overline{a} + D\frac{1}{2}\left( {3\cos^{2} \beta - 1} \right) + D^{\left( 2 \right)} \sin^{2} \beta \cos \left( {2\gamma } \right)} \right] \hfill \\ B = - 4\pi \left\{ {D\frac{3}{4}\sin \beta \cos \beta - D^{\left( 2 \right)} \frac{1}{2}\sin \beta \left[ {\cos \beta \cos \left( {2\gamma } \right) - i\sin \left( {2\gamma } \right)} \right]} \right\}, \hfill \\ \end{gathered}$$

(21)

where

$$\begin{gathered} \overline{g} = \frac{1}{3}\left( {g_{xx} + g_{yy} + g_{zz} } \right);\; \overline{a} = \frac{1}{3}\left( {A_{xx} + A_{yy} + A_{zz} } \right); F = \frac{2}{3}\left( {g_{zz} - \frac{1}{2}\left( {g_{xx} + g_{yy} } \right)} \right); \hfill \\ D = \frac{2}{3}\left( {A_{zz} - \frac{1}{2}\left( {A_{xx} + A_{yy} } \right)} \right);\; F^{\left( 2 \right)} = \frac{1}{2}\left( {g_{xx} - g_{yy} } \right); D^{\left( 2 \right)} = \frac{1}{2}\left( {A_{xx} - A_{yy} } \right). \hfill \\ \end{gathered}$$

(22)

Here ${\Omega }\left( {\eta ,\beta ,\gamma } \right) = \left( {0, - {\Theta },0} \right)$ are the Euler angles, which describe the orientation of the $\tilde{g}$ and $\tilde{A}$ matrices with respect to the static magnetic field, with $\Theta$ being the angle between the z axis of the magnetic frame and the Z-axis of the laboratory fixed frame.

The eigenvalues of the Hamiltonian, $\hat{H}_{0}$, as given by Eq. (20) are [1]

$$E_{a} = \frac{C}{2} + \frac{1}{2}\omega_{\alpha } ;\;E_{b} = \frac{C}{2} - \frac{1}{2}\omega_{\alpha } ;\;E_{c} = - \frac{C}{2} - \frac{1}{2}\omega_{\beta } ;\;E_{d} = - \frac{C}{2} + \frac{1}{2}\omega_{\beta } ,$$

(23)

where $\omega_{\alpha }$, $\omega_{\beta }$ are

$$\omega_{\alpha } = \left[ {\left( {\omega_{n} - \frac{A}{2}} \right)^{2} + \left( \frac{B}{2} \right)^{2} } \right]^{1/2} ;\;\omega_{\beta } = \left[ {\left( {\omega_{n} + \frac{A}{2}} \right)^{2} + \left( \frac{B}{2} \right)^{2} } \right]^{1/2} .$$

(24)

The eigenvectors are

$$\begin{gathered} \left| a \right. = \left[ {\begin{array}{*{20}c} {c_{1} } & { - c_{2} } & 0 & 0 \\ \end{array} } \right]^{{\text{T}}} ; |b = \left[ {\begin{array}{*{20}c} {c_{2} } & {c_{1} } & 0 & 0 \\ \end{array} } \right]^{{\text{T}}} \hfill \\ \left| c \right. = \left[ {\begin{array}{*{20}c} 0 & 0 & {c_{3} } & { - c_{4} } \\ \end{array} } \right]^{{\text{T}}} ; \left| d \right. = \left[ {\begin{array}{*{20}c} 0 & 0 & {c_{4} } & {c_{3} } \\ \end{array} } \right]^{{\text{T}}} , \hfill \\ \end{gathered}$$

(25)

where the superscript T denotes the transpose. The coefficient $c_{i} , i = 1, \ldots ,4$, in the above expressions are

$$\begin{gathered} c_{1} = \frac{1}{\sqrt 2 }\left[ {1 \pm \frac{{\left( {A/2} \right) - \omega_{n} }}{{\omega_{\alpha } }}} \right]^{1/2} ;c_{2} = - \frac{1}{\sqrt 2 }\left[ {1 \mp \frac{{\left( {A/2} \right) - \omega_{n} }}{{\omega_{\alpha } }}} \right]^{1/2} ; \hfill \\ c_{3} = \frac{1}{\sqrt 2 }\left[ {1 + \frac{{\left( {A/2} \right) + \omega_{n} }}{{\omega_{\beta } }}} \right]^{1/2} ;c_{4} = - \frac{1}{\sqrt 2 }\left[ {1 - \frac{{\left( {A/2} \right) + \omega_{n} }}{{\omega_{\beta } }}} \right]^{1/2} . \hfill \\ \end{gathered}$$

(26)

Here $\omega_{n}$ is the nuclear Larmor frequency.

Appendix B: Solution of Liouville von Neumann (LVN) equation

The equation of motion of the reduced density matrix, $\chi \left( t \right) = \rho \left( t \right) - \rho 0$, applicable during free evolution, i.e. in the absence of any time-dependent part in the Hamiltonian, is expressed as Liouville von Neumann (LVN) equation in Liouville space as follows [9,10,11,12,13,14,15].

$$\frac{{{\text{d}}\widehat{{\hat{\chi }}}}}{{{\text{d}}t}} = - i\widehat{{\hat{L}}}\widehat{{\hat{\chi }}} - \widehat{{\hat{R}}}\widehat{{\hat{\chi }}} = - \widehat{{\hat{L}}}^{\prime}\widehat{{\hat{\chi }}},$$

(27)

where $\widehat{{\hat{\chi }}}$ is the column vector in Liouville space corresponding to $\chi \left( t \right)$ in Hilbert space as defined above, $\widehat{{\hat{R}}}$ is the relaxation superoperator and $\widehat{{\hat{L}}}^{\prime}$ is the Liouvillian, which is defined as

$$\widehat{{\hat{L}}}^{^{\prime}} \equiv i\left[ {I_{4} \otimes \hat{H}_{0} - \left( {\hat{H}_{0} } \right)^{T} \otimes I_{4} } \right] + \widehat{{\hat{R}}},$$

(28)

with $\hat{H}_{0}$ being the spin Hamiltonian in Hilbert space and $I_{n}$ is a 4 $\times$ 4 identity matrix. The formal solution of Eq. (27) for $\widehat{{\hat{\chi }}}\left( t \right)$ after time t is expressed as

$$\widehat{{\hat{\chi }}}\left( t \right) = {\text{e}}^{{ - \left( {t - t_{0} } \right)\widehat{{\hat{L}}}^{^{\prime}} }} \widehat{{\hat{\chi }}}\left( {t_{0} } \right),$$

(29)

with the initial time being $t_{0}$.During the application of a pulse, the relaxation is neglected since the duration of the pulses, $t_{p}$, is much smaller than the relaxation times $T_{2e}$ and $T_{{{\text{2n}}}}$. The solution of the LVN equation after a pulse of duration $t_{p}$ is given by

$$\rho \left( {t_{0} + t_{p} } \right) = {\text{e}}^{{ - I\left( {\hat{H}_{0} + \hat{\varepsilon }} \right)t_{p} }} \rho \left( {t_{0} } \right){\text{e}}^{{I\left( {\hat{H}_{0} + \hat{\varepsilon }} \right)t_{p} }} ,$$

(30)

where the pulse, $\hat{\varepsilon }$, is expressed, in the rotating frame, as

$$\hat{\varepsilon } = B_{1} \gamma_{e} \left( {S_{x} \cos \phi + S_{y} \sin \phi } \right).$$

(31)

In Eq. (31) $\gamma_{e}$, $\phi$ and $B_{1}$ are the gyromagnetic ratio of the electron, the phase angle and amplitude of the pulse magnetic field, respectively,

The two-dimensional (2D) time-domain signal is calculated from $\rho_{{\text{f}}}$ as follows:

$$S\left( {t_{1} ,t_{2} } \right) = {\text{Tr}}(S_{ + } \rho_{{\text{f}}} ) = {\text{Tr}}\left( {\left( {S_{x} + iS_{y} } \right)\rho_{{\text{f}}} } \right).$$

(32)

The Fourier transform (FT) of the time domain signal $S\left( {t_{1} ,t_{2} } \right)$ is the corresponding 2D-FT signal, $S\left( {\omega_{1} ,\omega_{2} } \right)$.

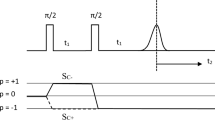
Both during a pulse and free evolution the calculations are carried in the rotating frame. At resonance, so that the effective magnetic field $B_{{{\text{eff}}}} = \left( {B - \frac{\hbar \omega }{{g\mu_{{\text{B}}} }}} \right)$ becomes zero. The echo-ELDOR calculations are made for the pulse sequences shown in Fig. 

Fig. 4

(Top) Figure to show the pulse sequence used for echo-ELDOR experiment. Here T_m is the mixing time, t₁ is the time between the first two pulses and the t₂ is stepped from the echo. (Bottom) Coherence pathways used in the echo-ELDOR experiment. Here $p$ represents the transverse magnetization, corresponding to spins rotating in a plan perpendicular to the external field [1]

4 for the coherent pathway $S_{c - }$ in accordance with that used in [1]. There are used two times, t₁ and t₂, which are stepped in the experiment (Fig. 4) for time-domain signals.

The signal is calculated over the coherent pathway $S_{c - }$ The values of the Spin-Hamiltonian parameters and the external magnetic field $\left( {B_{0} } \right)$ used are as follows [1]: the $\pi /2$ pulse is of duration $\sim 5\;{\text{ns}}$ [1];$\omega_{n} = 14.5\;{\text{MHz}}$; $\tilde{g} = \left( {g_{xx} , g_{yy} , g_{zz} } \right) = \left( {2.0026, 2.0035, 2.0033} \right)$; $\tilde{A} = \left( {A_{xx} , A_{yy} , A_{zz} } \right) = \left( { - 61.0\;{\text{MHz}}, - 91.0\;{\text{MHz}}, - 29.0\;{\text{MHz}}} \right)$. The Gaussian inhomogeneous broadening effect in the frequency domain along the axis $\omega_{2}$ $\left( { = 2\pi \nu } \right)$, corresponding to the step time $t_{2}$, as depicted in Fig. 3, is considered [1] by multiplying the time-domain signal with ${\text{e}}^{{ - 2\left( {\pi \Delta t_{2} } \right)^{2} }}$.

Full details of how to solve the LVN equation in the present case are described in [9, 10].