Skip to main content
SpringerLink
Log in

Biomechanics of the swimming of self-propelling spermatozoa through slippery human cervical canal

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

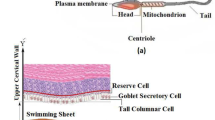
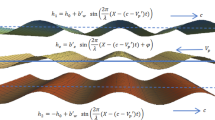
The present theoretical investigation is concerned with the biomechanics of the swimming of self-propelling spermatozoa through the slippery human cervical canal. Partial differential equations arising from the mathematical modelling of the proposed model along with slip boundary conditions are solved analytically. Expressions for pressure gradient, propulsive velocity, mucus velocity and time mean flow rate are analysed for the pertinent parameters. Salient features of the pumping characteristics are explored. It is interesting to note that maximal slippage on the upper cervical wall and zero slippage on the lower cervical wall maximize the probability of the spermatozoa to fertilize an ovum. It is found that a pressure rise facilitates the motion of spermatozoa to fertilize an ovum in the female reproductive tract, whereas a pressure drop inverts the direction of spermatozoa to the vagina and controls the probability of pregnancy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Taylor, G.I.: Analysis of the swimming of microscopic organisms. Proc. R. Soc. 209, 447–461 (1951)

    Article  MathSciNet  MATH  Google Scholar 

  2. Reynolds, A.J.: The swimming of minute organisms. J. Fluid Mech. 23, 241–260 (1965)

    Article  Google Scholar 

  3. Tuck, E.O.: A note on a swimming problem. J. Fluid Mech. 31, 305–308 (1968)

    Article  Google Scholar 

  4. Pak, O.S., Lauga, E.: The transient swimming of a waving sheet. Proc. R. Soc. 466, 107–126 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  5. Shack, W.J., Lardner, T.J.: A long wavelength solution for a microorganism swimming in a channel. Bull. Math. Biol. 36, 435–444 (1974)

    Article  MATH  Google Scholar 

  6. Smelser, R.E., Shack, W.J., Lardner, T.J.: The swimming spermatozoa in an active channel. J. Biomech. 7, 349–355 (1974)

    Article  Google Scholar 

  7. Odeblad, E.: Undulation of macromolecules in cervical mucus. Int. J. Fertil. 7, 313–319 (1962)

    Google Scholar 

  8. Shukla, J.B., Rao, B.R.P., Parihar, R.S.: Swimming of spermatozoa in cervix: effect of dynamical interaction and peripheral layer viscosity. J. Biomech. 11, 15–19 (1978)

    Article  Google Scholar 

  9. Sinha, P., Singh, C., Prasat, K.R.: A microcontinuum analysis of the self propulsion of the spermatozoa in the cervical canal. Int. J. Eng. Sci. 20, 1037–1048 (1982)

    Article  MATH  Google Scholar 

  10. Shukla, J.B., Chandra, P., Sharma, R., Radhakrishnamacharya, G.: Effects of peristaltic and longitudinal wave motion of the channel wall on movement of micro-organisms: application to spermatozoa transport. J. Biomech. 21, 947–954 (1988)

    Article  Google Scholar 

  11. Philip, D., Chandra, P.: Self-propulsion of spermatozoa in microcontinua: effect of transverse wave motion of channel walls. Arch. Appl. Mech. 66, 90–99 (1995)

    Article  MATH  Google Scholar 

  12. Radhakrishnamacharya, G., Sharma, R.: Motion of a self-propelling micro-organism in a channel under peristalsis: effects of viscosity variation. Nonlinear Anal. Model. Control 12, 409–418 (2007)

    MathSciNet  MATH  Google Scholar 

  13. Sathananthan, A.H.: Human centriole: origin, how it impacts fertilization, embryogenesis, infertility and cloning. Indian J. Med. Res. 129, 348–350 (2009)

    Google Scholar 

  14. Jones, R.E., Lopez, K.H.: Human Reproductive Biology, 3rd edn. Elsevier, Burlington (2006)

    Google Scholar 

  15. Neto, C., Evans, D.R., Bonaccurso, E., Butt, H.J., Craig, V.S.J.: Boundary slip in Newtonian liquids: a review of experimental studies. Rep. Prog. Phys. 68, 2859–2897 (2005)

    Article  Google Scholar 

  16. Lauga, E., Brenner, M.P., Stone, H.A.: Handbook of Experimental Fluid Dynamics. Edited by J. Foss, C. Tropea and A. Yarin. Springer, New York (2007)

    Google Scholar 

  17. Bocquet, L., Barrat, J.L.: Flow boundary conditions from nano- to micro-scales. Soft Matter 3, 685–693 (2007)

    Article  Google Scholar 

  18. Holt, J.K., Park, H.G., Wang, Y., Stadermann, M., Artyukhin, A.B., Grigoropoulos, C.P., Noy, A., Bakajin, O.: Fast mass transport through sub-2-nanometer carbon nanotubes. Science 312, 1034–1037 (2006)

    Article  Google Scholar 

  19. Majumder, M., Chopra, N., Andrews, R., Hinds, B.J.: Nanoscale hydrodynamics: enhanced flow in carbon nanotubes. Nature 438, 44 (2005)

    Article  Google Scholar 

  20. Ali, N., Hussain, Q., Hayat, T., Asghar, S.: Slip effects on the peristaltic transport of MHD fluid with variable viscosity. Phys. Lett. A 372, 1477–1489 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. Srinivas, S., Gayathri, R., Kothandapani, M.: The influence of slip conditions, wall properties and heat transfer on MHD peristaltic transport. Comput. Phys. Commun. 180, 2115–2122 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  22. Yildirim, A., Sezer, S.A.: Effects of partial slip on the peristaltic flow of a MHD Newtonian fluid in an asymmetric channel. Math. Comput. Model 52, 618–625 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  23. Hayat, T., Hussain, Q., Qureshi, M.U., Ali, N., Hendi, A.A.: Influence of slip condition on the peristaltic transport in an asymmetric channel with heat transfer: an exact solution. Int. J. Numer. Methods Fluids 67, 1944–1959 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  24. Tripathi, D., Gupta, P.K., Das, S.: Influence of slip condition on peristaltic transport of a viscoelastic fluid with fractional Burgers model. Therm. Sci. 15, 501–515 (2011)

    Article  Google Scholar 

  25. Akbar, N.S., Hayat, T., Nadeem, S., Obaidat, S.: Peristaltic flow of a Williamson fluid in an inclined asymmetric channel with partial slip and heat transfer. Int. J. Heat Mass Trans. 55, 1855–1862 (2012)

    Article  Google Scholar 

  26. Afsar Khan, A., Ellahi, R., Usman, M.: Effects of variable viscosity on the flow of non-Newtonian fluid through a porous medium in an inclined channel with slip conditions. J. Porous Media 16, 59–67 (2013)

    Article  Google Scholar 

  27. Hayat, T., Mehmood, O.U.: Slip effects on MHD flow of third order fluid in a planar channel. Commun. Nonlinear Sci. Numer. Simul. 16, 1363–1377 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  28. Ishijima, S., Oshio, S., Mohri, H.: Flagellar movement of human spermatozoa. Mol. Reprod. Dev. 13, 185–197 (1986)

    Google Scholar 

  29. Martyn, F., McAuliffe, F.M., Wingfield, M.: The role of the cervix in fertility: is it time for a reappraisal? Hum. Reprod. 29, 2092–2098 (2014)

    Article  Google Scholar 

  30. Munde, M.D.P.F.: Surgical Gynecology, A Manual Uterine Diagnosis and the Lesser Technicalities of Gynecological Practice for the Use of the Advance Students and General Practitioner. William Wood and Company, New York (1880)

    Google Scholar 

  31. Hatzikiriakos, S.G., Mitsoulis, E.: Slip effects in tapered dies. Polym. Eng. Sci. 49, 1960–1969 (2009)

    Article  Google Scholar 

  32. Papanastasiou, T., Georgiou, G., Alexandrou, A.N.: Viscous Fluid Flow. CRC Press, Boca Raton (1999)

    Book  MATH  Google Scholar 

  33. Gul, T., Shah, R.A., Islam, S., Arif, M.: MHD thin film flows of a third grade fluid on a vertical belt with slip boundary conditions. J. Appl. Math. 2013, 1–14 (2013)

    Article  MathSciNet  Google Scholar 

  34. Farooq, M., Rahim, M.T., Islam, S., Siddiqui, A.M.: Withdrawal and drainage of generalized second grade fluid on vertical cylinder with slip conditions. J. Prime Res. Math. 9, 51–64 (2013)

    MathSciNet  MATH  Google Scholar 

  35. Zaman, H.: Hall effects on the unsteady incompressible MHD fluid flow with slip conditions and porous walls. Appl. Math. Phys. 1, 31–38 (2013)

    Google Scholar 

  36. Ellahi, R., Hayat, T., Mahomed, F.M.: Generalized couette flow of a third-grade fluid with slip: the exact solutions. Zeitschrift Fr Naturforschung A 65, 1071–1076 (2010)

    Google Scholar 

Download references

Acknowledgements

The authors wish to express their very sincere thanks to the reviewers for their valuable suggestions and comments.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, Riphah International University, Sector I-14, Islamabad, Pakistan

    Ahsan Walait & M. A. Rana

  2. Department of Mathematics, Pennsylvania State University, York Campus, 1031 Edgecomb Avenue, York, PA, 17403, USA

    A. M. Siddiqui

Authors
  1. Ahsan Walait
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. M. Siddiqui
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. A. Rana
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahsan Walait.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Walait, A., Siddiqui, A.M. & Rana, M.A. Biomechanics of the swimming of self-propelling spermatozoa through slippery human cervical canal. Acta Mech 229, 2861–2881 (2018). https://doi.org/10.1007/s00707-018-2136-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-018-2136-0

Mathematics Subject Classification

Search

Navigation