Skip to main content
SpringerLink
Log in

Wave attenuation and negative refraction of elastic waves in a single-phase elastic metamaterial

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

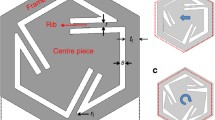
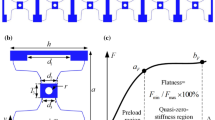
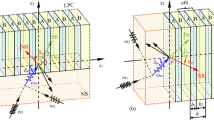
In this paper, we propose and study a single-phase elastic metamaterial with periodic chiral local resonator, which is composed of cylindrical central core surrounded by evenly distributed ligaments and embedded in the matrix in a square lattice. Based on the analytical and numerical analysis, we prove that the translational resonance of the unit cell can lead to negative effective mass density, and the rotational resonance of it can produce negative effective modulus. They can also work together to generate double-negative effective material properties. The wave attenuation of elastic waves in this elastic metamaterial is also demonstrated, which is owing to the negative effective mass density. In addition, the damping of the base material is also considered in the simulation. We finally examine the existence of negative band, and this leads to the physics of negative refraction, which is induced by simultaneous translational and rotational resonance of the unit cell. Our work can serve as the theoretical foundation for the design of single-phase elastic metamaterials.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Veselago, V.G.: The electrodynamics of substances with simultaneously negative values of \(\upvarepsilon \) and \(\upmu \). Sov. Phys. Usp. 10, 509–514 (1968)

    Article  Google Scholar 

  2. Pendry, J.B., Holden, A.J., Stewart, W.J., Youngs, I.: Extremely low frequency plasmons in metallic microstructures. Phys. Rev. Lett. 76, 4773–4776 (1996)

    Article  Google Scholar 

  3. Pendry, J.B., Holden, A.J., Robbins, D.J., Stewart, W.J.: Magnetism from conductors and enhanced nonlinear phenomena. Phys. Rev. Lett. 47, 2075–2084 (1999)

    Google Scholar 

  4. Seddon, N.: Observation of the Inverse Doppler effect. Science 302, 1537–1540 (2003)

    Article  Google Scholar 

  5. Schurig, D., Mock, J.J., Justice, B.J., Cummer, S.A., Pendry, J.B., Starr, A.F., Smith, D.R.: Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006)

    Article  Google Scholar 

  6. Alù, A., Engheta, N.: Plasmonic and metamaterial cloaking: physical mechanisms and potentials. J. Opt. A: Pure Appl. Opt. 10, 093002 (2008)

    Article  Google Scholar 

  7. Liu, Z., Chan, C.T., Sheng, P.: Analytic model of phononic crystals with local resonances. Phys. Rev. B 71, 014103 (2005)

    Article  Google Scholar 

  8. Bragg W.:The Diffraction of Short Electromagnetic Waves by a Crystal. In: Proceedings of the Cambridge Philosophical Society, vol. 17, pp. 43–57 (1913)

  9. Milton, G.W., Willis, J.R.: On modifications of Newton’s second law and linear continuum elastodynamics. Proc. R. Soc. A. 463, 855–880 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Yao, S., Zhou, X., Hu, G.: Investigation of the negative-mass behaviors occurring below a cut-off frequency. New J. Phys. 12, 103025 (2010)

    Article  Google Scholar 

  11. Huang, H., Sun, C., Huang, G.: On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 47, 610–617 (2009)

    Article  Google Scholar 

  12. Huang, G.L., Sun, C.T.: Band gaps in a multiresonator acoustic metamaterial. J. Vib. Acoust. 132, 031003 (2010)

    Article  Google Scholar 

  13. Huang, H., Sun, C.: Locally resonant acoustic metamaterials with 2D anisotropic effective mass density. Philos. Mag. 91, 981–996 (2011)

    Article  Google Scholar 

  14. Liu, X.N., Hu, G.K., Huang, G.L., Sun, C.T.: An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl. Phys. Lett. 98, 251907 (2011)

    Article  Google Scholar 

  15. Pai, P.F.: Metamaterial-based broadband elastic wave absorber. J. Intell. Mater. Syst. Struct. 21, 517–528 (2010)

    Article  Google Scholar 

  16. Sun, H., Chang, L., Du, X., Pai, P.: Theory and experiment research of metamaterial beams for broadband vibration absorption. J. Intell. Mater. Syst. Struct. 21, 1085–1101 (2010)

    Article  Google Scholar 

  17. Pai, P.F., Peng, H.: Acoustic metamaterial structures based on multi-frequency vibration absorbers. Int. J. Mech. Sci. 79, 195–205 (2014)

    Article  Google Scholar 

  18. Peng, H., Pai, P.F.: Acoustic metamaterial plates for elastic wave absorption and structural vibration suppression. Int. J. Mech. Sci. 89, 350–361 (2014)

    Article  Google Scholar 

  19. Zhu, R., Liu, X.N., Huang, G.L., Huang, H.H., Sun, C.T.: Microstructural design and experimental validation of elastic metamaterial plates with anisotropic mass density. Phys. Rev. B 86, 144307 (2012)

    Article  Google Scholar 

  20. Fang, N., Xi, D., Xu, J., Ambati, M., Srituravanich, W., Sun, C., Zhang, X.: Ultrasonic metamaterials with negative modulus. Nat. Mater. 5, 452–456 (2006)

    Article  Google Scholar 

  21. Ding, Y., Liu, Z., Qiu, C., Shi, J.: Metamaterial with simultaneously negative bulk modulus and mass density. Phys. Rev. Lett. 99, 093904 (2007)

    Article  Google Scholar 

  22. Lai, Y., Wu, Y., Sheng, P.: Hybrid elastic solids. Nat. Mater. 10, 620–6244 (2011)

    Article  Google Scholar 

  23. Wu, Y., Lai, Y., Zhang, Z.-Q.: Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys. Rev. Lett. 107, 105506 (2011)

    Article  Google Scholar 

  24. Li, J., Chan, C.: Double-negative acoustic metamaterial. Phys. Rev. E 70, 055602 (2004)

    Article  Google Scholar 

  25. Liu, X., Hu, G., Sun, C., Huang, G.: Wave propagation characterization and design of two-dimensional elastic chiral metacomposite. J. Sound Vib. 330, 2536–2553 (2011)

    Article  Google Scholar 

  26. Liu, X., Huang, G., Hu, G.: Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices. J. Mech. Phys. Solids 60, 1907–1921 (2012)

    Article  MathSciNet  Google Scholar 

  27. Zhu, R., Liu, X., Hu, G., Sun, C., Huang, G.: A chiral elastic metamaterial beam for broadband vibration suppression. J. Sound Vib. 333, 2759–2773 (2014)

    Article  Google Scholar 

  28. Zhu, R., Liu, X.N., Hu, G.K., Sun, C.T., Huang, G.L.: Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat. Commun. 5, 5510 (2014)

    Article  Google Scholar 

Download references

Acknowledgements

We appreciate the financial support from the National Natural Science Foundation of China (Grants No. 11402101).

Author information

Authors and Affiliations

  1. Department of System Engineering, University of Arkansas at Little Rock, Little Rock, AR, 72204, USA

    Sheng Sang & Eric Sandgren

  2. Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang, 212013, China

    Sheng Sang & Ziping Wang

Authors
  1. Sheng Sang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Eric Sandgren
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ziping Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sheng Sang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sang, S., Sandgren, E. & Wang, Z. Wave attenuation and negative refraction of elastic waves in a single-phase elastic metamaterial. Acta Mech 229, 2561–2569 (2018). https://doi.org/10.1007/s00707-018-2127-1

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-018-2127-1

Search

Navigation