Abstract
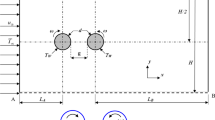
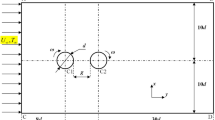
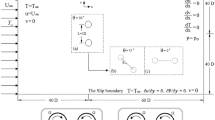
This paper discusses the forced convective heat transfer and fluid flow around two counter-rotating cylinders in tandem arrangement at a constant Reynolds number of 200. The upstream and downstream cylinders rotate in counterclockwise and clockwise directions, respectively, with an identical non-dimensional rotating speed (RS) in the range of \(0\le \hbox {RS}\le 4\). Computations are carried out at various non-dimensional gap spaces between the cylinders such as the \({G{/}D}=1.5\), 2.0, and 3.0. It is found that counter-rotating the tandem cylinders deforms the wake region downstream of both cylinders in which the vortex strength of the upstream cylinder is realized to be stronger at larger gap spaces. On the other hand, it is stated that the instabilities of the shear layer of both cylinders become maximum and minimum at \(\hbox {RS}=1\) and \(\hbox {RS}=2\), respectively. Examination of the Nusselt number distributions on the cylinders indicates that at the high RS values, more or less, all points on the each individual cylinder have identical roles in the heat dissipation rate. Finally, it is concluded that the maximum heat transfer occurs at \(\hbox {RS}=1\) for both cylinders.
Similar content being viewed by others
Abbreviations
- A :
-
Projected area
- \(C_\mathrm{D} \) :
-
Drag coefficient (\({=}\,\frac{F_\mathrm{D}}{0.5\rho U^{2}A})\)
- \(\bar{{C}}_\mathrm{D} \) :
-
Mean drag coefficient
- \(C_\mathrm{L}\) :
-
Lift coefficient (\({=}\,\frac{F_\mathrm{L}}{0.5\rho U^{2}A})\)
- \(\bar{{C}}_\mathrm{L}\) :
-
Mean lift coefficient
- \(C_\mathrm{p} \) :
-
Pressure coefficient (\({=}\,\frac{p-p_\infty }{0.5\rho U^{2}})\)
- \(c_\mathrm{p} \) :
-
Specific pressure
- D :
-
Cylinder diameter
- \(F_\mathrm{D}\) :
-
Drag force
- \(F_\mathrm{L}\) :
-
Lift force
- G :
-
Gap space between the cylinders
- k :
-
Conductivity
- n :
-
Surface vertical vector
- Nu :
-
Nusselt number
- \(\overline{Nu} \) :
-
Mean Nusselt number
- \(p_\infty \) :
-
Free-stream pressure
- p :
-
Pressure
- Pr :
-
Prandtl number (\({=}\,\frac{\mu c_\mathrm{p}}{k})\)
- r :
-
Radial coordinate
- R :
-
Cylinder radius
- Re :
-
Reynolds number (\({=}\,\frac{\rho UD}{\mu })\)
- RS:
-
Non-dimensional rotational speed \(({=}\,\frac{\omega D}{2U})\)
- t :
-
Time
- T :
-
Temperature
- \(T_\infty \) :
-
Free-stream temperature
- u :
-
Streamwise velocity
- \(\bar{{u}}\) :
-
Time-averaged streamwise velocity
- U :
-
Free-stream velocity
- \(u_\mathrm{{rms}} \) :
-
Root-mean-square of the streamwise velocity
- v :
-
Vertical velocity
- \(\bar{{v}}\) :
-
Time-averaged vertical velocity
- \(v_\mathrm{{rms}} \) :
-
Root-mean-square of the vertical velocity
- x :
-
Streamwise dimension of coordinates
- y :
-
Vertical dimension of coordinates
- \(\mu \) :
-
Dynamic viscosity of the fluid
- \(\upsilon \) :
-
Kinematic viscosity of the fluid
- \(\rho \) :
-
Density of the fluid
- \(\alpha \) :
-
Angular location
- \(\omega \) :
-
Rotating speed
- \(\xi \) :
-
Element size
- 1:
-
Upstream cylinder
- 2:
-
Downstream cylinder
- \(\max \) :
-
Maximum
- \(\min \) :
-
Minimum
- s:
-
Surface of the cylinder
- \(\infty \) :
-
Free-stream
References
Rajani, B.N., Kandasamy, A., Majumdar, S.: Numerical simulation of laminar flow past a circular cylinder. Appl. Math. Model. 33, 1228–1247 (2009)
Ramos-García, N., Sarlak, H., Andersen, S.J., Sørensen, J.N.: Simulation of the flow past a circular cylinder using an unsteady panel method. Appl. Math. Model. 44, 206–222 (2017)
Abrahamsen Prsic, M., Ong, M.C., Pettersen, B., Myrhaug, D.: Large Eddy Simulations of flow around a smooth circular cylinder in a uniform current in the subcritical flow regime. Ocean Eng. 77, 61–73 (2014)
Durante, D., Rossi, E., Colagrossi, A., Graziani, G.: Numerical simulations of the transition from laminar to chaotic behaviour of the planar vortex flow past a circular cylinder. Commun. Nonlinear Sci. Numer. Simul. 48, 18–38 (2017)
Stringer, R.M., Zang, J., Hillis, A.J.: Unsteady RANS computations of flow around a circular cylinder for a wide range of Reynolds numbers. Ocean Eng. 87, 1–9 (2014)
Rajagopalan, S., Antonia, R.A.: Flow around a circular cylinder–structure of the near wake shear layer. Exp. Fluids 38, 393–402 (2005)
Yeon, S.M., Yang, J., Stern, F.: Large-eddy simulation of the flow past a circular cylinder at sub- to super-critical Reynolds numbers. Appl. Ocean Res. 59, 663–675 (2016)
Aljure, D.E., Lehmkhul, O., Rodríguez, I., Oliva, A.: Three dimensionality in the wake of the flow around a circular cylinder at Reynolds number 5000. Comput. Fluids. 147, 102–118 (2017)
Perret, L.: PIV investigation of the shear layer vortices in the near wake of a circular cylinder. Exp. Fluids 47, 789–800 (2009)
Kang, S.: Uniform-shear flow over a circular cylinder at low Reynolds numbers. J. Fluids Struct. 22, 541–555 (2006)
Alam, MdM, Zheng, Q., Hourigan, K.: The wake and thrust by four side-by-side cylinders at a low Re. J. Fluids Struct. 70, 131–144 (2017)
Chen, W., Ji, C., Wang, R., Xu, D., Campbell, J.: Flow-induced vibrations of two side-by-side circular cylinders: asymmetric vibration, symmetry hysteresis and near-wake patterns. Ocean Eng. 110, 244–257 (2015)
Elhimer, M., Harran, G., Hoarau, Y., Cazin, S., Marchal, M., Braza, M.: Coherent and turbulent processes in the bistable regime around a tandem of cylinders including reattached flow dynamics by means of high-speed PIV. J. Fluids Struct. 60, 62–79 (2016)
Gopalan, H., Jaiman, R.: Numerical study of the flow interference between tandem cylinders employing non-linear hybrid URANS-LES methods. J. Wind Eng. Ind. Aerodyn. 142, 111–129 (2015)
Kim, S., Alam, MdM: Characteristics and suppression of flow-induced vibrations of two side-by-side circular cylinders. J. Fluids Struct. 54, 629–642 (2015)
Liu, J., Xie, G., Sundén, B.: Flow pattern and heat transfer past two tandem arranged cylinders with oscillating inlet velocity. Appl. Therm. Eng. 120, 614–625 (2017)
Pang, J.H., Zong, Z., Zou, L., Wang, Z.: Numerical simulation of the flow around two side-by-side circular cylinders by IVCBC vortex method. Ocean Eng. 119, 86–100 (2016)
Thapa, J., Zhao, M., Cheng, L., Zhou, T.: Three-dimensional simulations of flow past two circular cylinders in side-by-side arrangements at right and oblique attacks. J. Fluids Struct. 55, 64–83 (2015)
Tu, J., Zhou, D., Bao, Y., Ma, J., Lu, J., Han, Z.: Flow-induced vibrations of two circular cylinders in tandem with shear flow at low Reynolds number. J. Fluids Struct. 59, 224–251 (2015)
Vakil, A., Green, S.I.: Two-dimensional side-by-side circular cylinders at moderate Reynolds numbers. Comput. Fluids. 51, 136–144 (2011)
Karabelas, S.J.: Large Eddy simulation of high-Reynolds number flow past a rotating cylinder. Int. J. Heat Fluid Flow 31, 518–527 (2010)
Lam, K.M.: Vortex shedding flow behind a slowly rotating circular cylinder. J. Fluids Struct. 25, 245–262 (2009)
Thakur, P., Mittal, S., Tiwari, N., Chhabra, R.P.: The motion of a rotating circular cylinder in a stream of Bingham plastic fluid. J. Nonnewton. Fluid Mech. 235, 29–46 (2016)
Ghazanfarian, J., Nobari, M.R.H.: A numerical study of convective heat transfer from a rotating cylinder with cross-flow oscillation. Int. J. Heat Mass Transf. 52, 5402–5411 (2009)
Ikhtiar, U., Manzoor, S., Sheikh, N.A., Ali, M.: Free stream flow and forced convection heat transfer around a rotating circular cylinder subjected to a single gust impulse. Int. J. Heat Mass Transf. 99, 851–861 (2016)
Mittal, S., Kumar, B.: Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334 (2003)
Stojković, D., Breuer, M., Durst, F.: Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 14(9), 3160–3178 (2002)
Patankar, S.V.: Numerical Heat Transfer and Fluid Flow. Taylor & Francis, New York (1980)
Meneghini, J.R., Siqueira, Cd.L.R., Saltara, F., Ferrari, Jr. J.A.: An investigation of the flow around two circular cylinders in tandem arrangements, \(15{{\rm th}}\) Brazilian congress of mechanical engineering, Sao Paulo, November 22–26
Slaoutian, A., Stansby, P.K.: Flow around two circular cylinders by the random-vortex method. J. Fluids Struct. 6, 641–670 (1992)
Mahir, N., Altaç, Z.: Numerical investigation of convective heat transfer in unsteady flow past two cylinders in tandem arrangements. Int. J. Heat Fluid Flow 29, 1309–1318 (2008)
R. Hilpert, Forsch. Geb. Ingenieurwes 4, 215 (1933)
Churchill, S.W., Bernstein, M.: A correlation equation for forced convection from gases and liquids to a circular cylinder in cross Flow. ASME J. Heat Transf. Trans. 94, 300–306 (1977)
Harimi, I., Saghafian, M.: Numerical simulation of fluid flow and forced convection heat transfer from tandem circular cylinders using overset grid method. J. Fluids Struct. 28, 309–327 (2012)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Darvishyadegari, M., Hassanzadeh, R. Convective heat transfer and fluid flow of two counter-rotating cylinders in tandem arrangement. Acta Mech 229, 1783–1802 (2018). https://doi.org/10.1007/s00707-017-2070-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-017-2070-6