Skip to main content
SpringerLink
Log in

Functionally graded piezoelectric–piezomagnetic fibrous composites

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

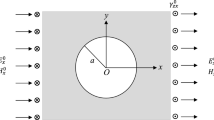
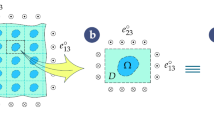
We investigate the magnetoelectric effect and potential fields of functionally graded multiferroic fibrous composites under anti-plane shear deformation coupled to in-plane electric and magnetic fields. The cylinders are exponentially graded along the radial direction. Rayleigh’s formalism and composite cylinder assemblage model are generalized to account for the configuration. We find that the grading parameter has a dramatic effect on the potential field of the inclusion and the effective property of the composite. We adopt this approach to numerically study the exponentially graded \(\hbox {BaTiO}_{3}\hbox {--CoFe}_{2}\hbox {O}_{4}\) composite and provide insights into developing new multiferroic fibrous media with high magnetoelectric coupling.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Arefi, M.: Analysis of wave in a functionally graded magneto-electro-elastic nano-rod using nonlocal elasticity model subjected to electric and magnetic potentials. Acta Mech. 227, 2529–2542 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  2. Arfken, G.B., Weber, H.J.: Mathematical Methods for Physicists. Academic Press, San Diago (2001)

    MATH  Google Scholar 

  3. Bhangale, R.K., Ganesan, N.: Static analysis of simply supported functionally graded and layered magneto-electro-elastic plates. Int. J. Solids Struct. 43, 3230–3253 (2006)

    Article  MATH  Google Scholar 

  4. Benveniste, Y.: Magnetoelectric effect in fibrous composites with piezoelectric and piezomagnetic phases. Phys. Rev. B 51, 16424–16427 (1995)

    Article  Google Scholar 

  5. Chen, T., Kuo, H.-Y.: Transport properties of composites consisting of periodic arrays of exponentially graded cylinders with cylindrically orthotropic materials. J. Appl. Phys. 98, 033716 (2005)

    Article  Google Scholar 

  6. Feng, W.J., Pan, E.: Dynamic fracture behavior of an internal interfacial crack between two dissimilar magneto-electro-elastic plates. Eng. Fract. Mech. 75, 1468–1487 (2008)

  7. Fiebig, M.: Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 38, R123–R152 (2005)

    Article  Google Scholar 

  8. Han, X., Liu, G.R.: Elastic waves in a functionally graded piezoelectric cylinder. Smart Mater. Struct. 12, 962–971 (2003)

    Article  Google Scholar 

  9. Hashin, Z., Rosen, B.W.: The elastic moduli of fiber-reinforced materials. J. Appl. Mech. 31, 223–232 (1964)

    Article  Google Scholar 

  10. Huang, J.H., Kuo, W.-S.: The analysis of piezoelectric/piezomagnetic composite materials containing ellipsoidal inclusions. J. Appl. Phys. 81, 1378–1386 (1997)

    Article  Google Scholar 

  11. Kuo, H.-Y.: Electrostatic interactions of arbitrarily dispersed multicoated elliptic cylinders. Int. J. Eng. Sci. 48, 370–382 (2010)

    Article  Google Scholar 

  12. Kuo, H.-Y.: Multicoated elliptical fibrous composites of piezoelectric and piezomagnetic phases. Int. J. Eng. Sci. 49, 561–575 (2011)

    Article  MATH  Google Scholar 

  13. Kuo, H.-Y., Bhattacharya, K.: Fibrous composites of piezoelectric and piezomagnetic phases. Mech. Mater. 60, 159–170 (2013)

    Article  Google Scholar 

  14. Kuo, H.-Y., Chen, T.: Effective transport properties of arrays of multicoated or graded spheres with spherically transversely isotropic constituents. J. Appl. Phys. 99, 093702 (2006)

    Article  Google Scholar 

  15. Kuo, H.-Y., Chen, T.: Electrostatic fields of an infinite medium containing arbitrarily positioned coated cylinders. Int. J. Eng. Sci. 46, 1157–1172 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kuo, H.-Y., Pan, E.: Effective magnetoelectric effect in multicoated circular fibrous multiferroic composites. J. Appl. Phys. 109, 104901 (2011)

    Article  Google Scholar 

  17. Kuo, H.-Y., Wang, Y.-L.: Optimization of magnetoelectricity in multiferroic fibrous composites. Mech. Mater. 50, 88–99 (2012)

    Article  Google Scholar 

  18. Lazar, M.: On the screw dislocation in a functionally graded material. Mech. Res. Commun. 34, 305–311 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  19. Li, P., Wen, Y., Liu, P., Li, X., Jia, C.: A magnetoelectric energy harvester and management circuit for wireless sensor network. Sens. Actuators, A 157, 100–106.41 (2010)

    Article  Google Scholar 

  20. Liu, L., Kuo, H.-Y.: Closed-form solutions to the effective properties of fibrous magnetoelectric composites and their applications. Int. J. Solids Struct. 49, 3055–3062 (2012)

    Article  Google Scholar 

  21. Liu, G., Nan, C.-W., Cai, N., Lin, Y.: Dependence of giant magnetoelectric effect on interfacial bonding for multiferroic laminate composites of rare-earth-iron alloys and lead-zirconate-titanate. J. Appl. Phys. 95, 2660–2664 (2004)

    Article  Google Scholar 

  22. Liu, Y.X., Wang, J.G., Nan, C.W.: Numerical modeling of magnetoelectric effect in a composite structure. J. Appl. Phys. 94, 5111–5117 (2003)

    Article  Google Scholar 

  23. Liu, Q., Zhao, M., Zhang, C.: Antiplane scattering of SH waves by a circular cavity in an exponentially graded half space. Int. J. Eng. Sci. 78, 61–72 (2014)

    Article  MathSciNet  Google Scholar 

  24. Lutz, M.P., Zimmerman, R.W.: Effect of the interphase zone on the conductivity or diffusivity of particulate composite using Maxwell’s homogenization method. Int. J. Eng. Sci. 98, 51–59 (2016)

    Article  Google Scholar 

  25. Ma, J., Ke, L.-L., Wang, Y.-S.: Sliding frictional contact of functionally graded magneto-electro-elastic materials under a conducting flat punch. Trans. ASME J. Appl. Mech. 82, 011009 (2015)

    Article  Google Scholar 

  26. Ma, L., Wu, L.-Z., Feng, L.-P.: Surface crack problem for functionally graded magnetoelectroelastic coating-homogeneous elastic substrate system under anti-plane mechanical and in-plane electric and magnetic loading. Eng. Fract. Mech. 76, 269–285 (2009)

    Article  Google Scholar 

  27. Markworth, A.J., Ramesh, K.S., Parks Jr., W.P.: Modelling studies applied to functionally graded materials. J. Mater. Sci. 30, 2183–2193 (1995)

    Article  Google Scholar 

  28. Martin, P.A.: On functionally graded balls and cones. J. Eng. Math. 42, 133–142 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  29. Martin, P.A.: Scattering by a cavity in an exponentially graded half-space. Trans. ASME J. Appl. Mech. 76, 031009 (2009)

    Article  Google Scholar 

  30. Mousavi, S.M.: Dislocation-based fracture analysis of functionally graded magnetoelectroelastic solids. Z. Angew. Math. Mech. 95, 1501–1513 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  31. Mousavi, S.M., Paavola, J.: Analysis of functionally graded magneto-electro-elastic layer with multiple cracks. Theor. Appl. Fract. Mech. 66, 1–8 (2013)

    Article  Google Scholar 

  32. Nan, C.-W., Li, M., Huang, J.H.: Calculations of giant magnetoelectric effects in ferroic composites of rare-earth-iron alloys and ferroelectric polymers. Phys. Rew. B 63, 144415 (2001)

    Article  Google Scholar 

  33. Palneedi, H., Annapureddy, V., Priya, S., Ryu, J.: Status and perspectives of multiferroic magnetoelectric composite materials and applications. Actuators 5, 9 (2016)

    Article  Google Scholar 

  34. Shodja, H.M., Eskandari, S., Eskandari, M.: Shear horizontal surface acoustic waves in functionally graded magneto-electro-elastic half-space. J. Eng. Math. 97, 83–100 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  35. Sladek, J., Sladek, V., Krahulec, S., Pan, E.: Enhancement of the magnetoelectric coefficient in functionally graded multiferroic composites. J. Intell. Mater. Syst. Struct. 23, 1649–1658 (2012)

    Article  Google Scholar 

  36. Sladek, J., Sladek, V., Krahulec, S., Pan, E.: Analyses of functionally graded plates with magnetoelectroelastic layer. Smart Mater. Struct. 22, 035003 (2013)

    Article  MATH  Google Scholar 

  37. Suresh, S.: Graded materials for resistance to contact deformation and damage. Science 292, 2447–2451 (2001)

    Article  Google Scholar 

  38. Wang, Y.-Z., Kuna, M.: Screw dislocation in functionally graded magnetoelectroelastic solids. Philos. Mag. Lett. 94, 72–79 (2014)

    Article  Google Scholar 

  39. Wang, X., Pan, E.: Magnetoelectric effects in multiferroic fibrous composite with imperfect interface. Phys. Rev. B 76, 214107 (2007)

    Article  Google Scholar 

  40. Wang, R., Pan, E.: Three-dimensional modeling of functionally graded multiferroic composites. Mech. Adv. Mater. Struct. 18, 68–76 (2011)

    Article  Google Scholar 

  41. Wang, X., Pan, E., Albrecht, J.D., Feng, W.J.: Effective properties of multilayered functionally graded multiferroic composites. Compos. Struct. 87, 206–214 (2009)

    Article  Google Scholar 

  42. Wu, C.-P., Tsai, Y.-H.: Dynamic responses of functionally graded magneto-electro-elastic shells with closed-circuit surface conditions using the method of multiple scales. Europ. J. Mech. A Solids 29, 166–181 (2010)

    Article  MathSciNet  Google Scholar 

  43. Xue, C.X., Pan, E.: On the longitudinal wave along a functionally graded magneto-electro-elastic rod. Int. J. Eng. Sci. 62, 48–55 (2013)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, National Chiao Tung University, Hsinchu, 30010, Taiwan

    Hsin-Yi Kuo & Kai-Chi Hsin

Authors
  1. Hsin-Yi Kuo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kai-Chi Hsin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hsin-Yi Kuo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kuo, HY., Hsin, KC. Functionally graded piezoelectric–piezomagnetic fibrous composites. Acta Mech 229, 1503–1516 (2018). https://doi.org/10.1007/s00707-017-2065-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-017-2065-3

Search

Navigation