Abstract
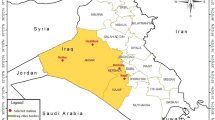
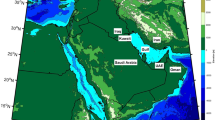
Analysis of the daily surface solar radiation (SSR) data over the 12 stations spread across India revealed that the data have many missing values and significant variability, which induce large uncertainties in the seasonal and annual means. Since the number of missing values and data variability change over time, ignoring them in the trend analysis, as done in most previous studies, may lead to erroneous results. We propose a method to incorporate the data uncertainty in the trend analysis and compare it with the traditional method, that ignores uncertainty, using the synthetic data with a known trend and having a different percentage of missing values. The proposed method is able to capture the trends in more than 85% of the cases, whereas the traditional method does it for less than 70% of the cases. Analysis of the SSR data by the proposed method revealed a renewed stronger solar dimming of about − 45 W/m2 per decade over the last decade (2006–2015) at all the 12 stations. Analysis of an independent satellite-derived SSR data from the Breathing Earth System Simulator (generated using the MODIS satellite data) also showed the significantly decreasing trends of about − 20 W/m2 per decade in the annual SSR over the entire India. The SSR proxies (sunshine duration and diurnal temperature range) and the wind speed also exhibited the trends consistent with the renewed dimming and suggest that it can be attributed to the increasing aerosol concentration over India in the recent decade.









Similar content being viewed by others
References
Brunetti M, Maugeri M, Monti F, Nanni T (2006) Temperature and precipitation variability in Italy in the last two centuries from homogenised instrumental time series. Int J Climatol 26(3):345–381
Hannah J (2004) An updated analysis of long-term sea level change in New Zealand. Geophys Res Lett 31 (3):0094–8276. https://doi.org/10.1029/2003GL019166
Kaplan E, Meier P (1958) Nonparametric estimation from incomplete observations. J Am Stat Assoc 53 (282):457–481
Karl TR, Arguez A, Huang B, Lawrimore JH, McMahon JR, Menne MJ, Peterson TC, Vose RS, Zhang H-M (2015) Possible artifacts of data biases in the recent global surface warming hiatus. Science 5632
Lagarias JC, Reeds JA, Wright MH, Wright P (1998) Convergence properties of the Nelder–Mead simplex method in low dimensions. SIAM J Optim 9(1):112–147
Manara V, Brunetti M, Celozzi A, Maugeri M, Sanchez-Lorenzo A, Wild M (2016) Detection of dimming/brightening in Italy from homogenized all-sky and clear-sky surface solar radiation records and underlying causes. Atmos Chem Phys 16(17):11145– 11161
More S, Pradeep Kumar P, Gupta P, Devara PCS, Aher GR (2013) Comparison of aerosol products retrieved from AERONET, MICROTOPS and MODIS over a tropical urban city, Pune. Aerosol Air Qual Res 13 (1):107–121
Padma Kumari B, Goswami BN (2010) Seminal role of clouds on solar dimming over the Indian monsoon region. Geophys Res Lett 37(6):L06703. https://doi.org/10.1029/2009GL042133
Padma Kumari B, Londhe AL, Daniel S, Jadhav DB (2007) Observational evidence of solar dimming: offsetting surface warming over India. Geophys Res Lett 34(21):L21810. https://doi.org/10.1029/2007GL031133
Roesch A, Wild M, Ohmura A, Dutton EG, Long CN, Zhang T (2011) Assessment of BSRN radiation records for the computation of monthly means. Atmos Meas Tech 4(2):339– 354
Ryu Y, Jiang C, Kobayashi H, Detto M (2018) MODIS-derived global land products of shortwave radiation and diffuse and total photosynthetically active radiation at 5 km resolution from 2000. Remote Sens Environ 204:812–825
Soni VK, Pandithurai G, Pai DS (2012) Evaluation of long-term changes of solar radiation in India. Int J Climatol 32(4):540– 551
Soni VK, Pandithurai G, Pai DS (2016) Is there a transition of solar radiation from dimming to brightening over India?. Atmos Res 169:209–224
Taylor JR (1997) An introduction to error analysis: the study of uncertainties in physical measurements, University Science Books
Tripathi SN, Dey S, Chandel A, Srivastava S, Singh RP, Holben BN (2005) Comparison of MODIS and AERONET derived aerosol optical depth over the Ganga Basin, India. Annales Geophysicae 23(4):1093–11012009
Wang K, Dickinson RE (2013) Contribution of solar radiation to decadal temperature variability over land. Proc Natl Acad Sci 110(37):14,877–14,882
Wild M (2009) Global dimming and brightening: a review. J Geophys Res-Atmos 114:D00D16. https://doi.org/10.1029/2008JD011470
Wild M (2012) Enlightening global dimming and brightening. Bull Am Meteorol Soc 93(1):27
Wild M, Ohmura A, Makowski K (2007) Impact of global dimming and brightening on global warming. Geophys Res Lett 34(4):L04702. https://doi.org/10.1029/2006GL028031
Wild M, Grieser J, Schär C (2008) Combined surface solar brightening and increasing greenhouse effect support recent intensification of the global land-based hydrological cycle. Geophys Res Lett 35(17):L17706. https://doi.org/10.1029/2008GL034842
WMO (1983) Guide to meteorological instruments and methods of observation. Chap. 9
Xu M, Chang CP, Fu C, Qi Y, Robock A, Robinson D, Zhang HM (2006) Steady decline of east Asian monsoon winds, 1969–2000: evidence from direct ground measurements of wind speed. J Geophys Res-Atmos 111:D24111. https://doi.org/10.1029/2006JD007337
Yoon J, von Hoyningen-Huene W, Kokhanovsky AA, Vountas M, Burrows JP (2012) Trend analysis of aerosol optical thickness and Angstrom exponent derived from the global AERONET spectral observations. Atmos Meas Tech 5(6):1271
Acknowledgments
The authors are thankful to Dr. Martin Wild for his comments/suggestions that helped us to significantly improve this manuscript. The authors thank IMD for providing the SSR, diffuse radiation, sunshine duration, and wind speed data. We also thank MODIS for providing the AOD and cloud fraction data which were obtained from GIOVANI (https://giovanni.gsfc.nasa.gov/giovanni/) website. We are thankful to GHCM for providing the monthly mean maximum and minimum temperature data (https://www.ncdc.noaa.gov/ghcnm/v3.php). We also thank WRDC for providing the radiation data which are available at http://wrdc.mgo.rssi.ru/.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix A: Weighted linear regression (WLR)
The seasonal (or annual) SSR anomalies (μy) and corresponding standard errors (εy) were employed in weighted linear regression (WLR) to find the trends. The equation of the trend line fitted by the WLR method is given by the Eq. 13, in which A and B represent the slope and the intercept, respectively.
A and B were found using Eqs. 14 and 15 (Taylor 1997).
where,
In the equations above, ty and μy represent year and seasonal (or annual) SSR anomaly, respectively, for the y th data point, and Nyears denotes the number of years for which data are available. The weights (wy) are inversely proportional to the square of the standard error (εy) of SSR anomaly μy. The model error (σM) is given by Eq. 17 and the uncertainties in slope (ΔA) and intercept (ΔB) are given by Eqs. 18 and 19, respectively.
where \(T_{i}^{\prime }s\) are given by the following:
Appendix B: Generation of synthetic data
Following steps were used for generating 30 years of synthetic daily SSR data:
-
1.
Monthly mean (\({M_{_{y,m}}}\)) and standard deviation (\({S_{_{y,m}}}\)) for the first year (i.e., y = 1) were specified. To make simulations reaslistic, \({M_{_{1,m}}}\) and \({S_{_{1,m}}}\) were estimated using daily SSR data of the Pune station (mean and standard deviations are given in Table S1).
-
2.
A decreasing trend of − 1.0 W/m2 per year was induced for estimating monthly means for the remaining years using the following equations.
$$ {M_{y + 1,m}} = {M_{y,m}} - 1 \left\{ {\begin{array}{*{20}{c}} {y = 1,2,\ldots,29}\\ {m = 1,2,\ldots,12} \end{array}} \right. $$(20)The monthly standard deviations were assumed to be constant, i.e.,
$$ {S_{y + 1,m}} = {S_{y,m}} \left\{ {\begin{array}{*{20}{c}} {y = 1,2,\ldots,29}\\ {m = 1,2,\ldots,12} \end{array}} \right. $$(21) -
3.
The daily SSR values for the month (m) and the year (y) were generated as independent random samples from the normal distribution with mean My,m and standard deviation Sy,m. Five hundred random samples were generated to create 500 sets of 30 years of the daily SSR data.
-
4.
From the daily SSR data, thus generated, some data were randomly (5 to 20 days per month) removed to create a missing data set. The random removal was performed 10 times to create 5000 (10× 500) simulations of the missing dataset. Two groups of missing datasets were simulated. In the first group, data were removed from all the months in all the years and in the second group, data were removed only from the monsoon months of each year. The later group was generated to mimic the observed records where most of the missing observations are present during the monsoon season.
-
5.
Annual trends in the simulated datasets were estimated using the WLR and LR methods as described in Section 3.
Rights and permissions
About this article
Cite this article
Soni, P., Srivastava, R. & Tripathi, S. Implication of data uncertainty in the detection of surface radiation trends and observational evidence of renewed solar dimming over India. Theor Appl Climatol 137, 2663–2680 (2019). https://doi.org/10.1007/s00704-018-2743-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-018-2743-7