Abstract
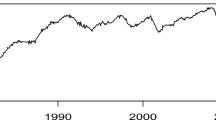
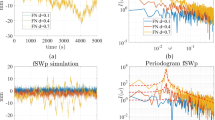
The global monthly temperature anomaly time series for the period 1850–2012 has been investigated in terms of multifractal detrended fluctuation analysis (MF-DFA). Various multifractal observables, such as the generalized Hurst exponent, the multifractal exponent, and the singularity spectrum, are extracted and are fitted to a generalized binomial multifractal model consists of only two free parameters. The results of this analysis give a clear indication of the presence of long-term memory in the global temperature anomaly time series which causes multifractal pattern in the data. We investigate the possible other source(s) of multifractality in the series by random shuffling as well as by surrogating the original series and find that the probability density function also contributes to the observed multifractal pattern along with the long-memory effect. Surprisingly, the temperature anomaly time series are well described by the two-parameter multifractal binomial model.




Similar content being viewed by others
Notes
Autocorrelations between two x i values separated by n steps (lags) in the same series are defined by \(C(n)=\left < x_{i} x_{i+n}\right > \).
References
Ashkenazy Y, Baker DR, Gildor H, Havlin H (2003) Nonlinearity and multifractality of climate change in the past 420,000 years. Geophys Res Lett 30:2146–2151
Bachelier L (1900) Théorie de la spéculation. Ann Sci l’École Norm Supéure 17(3):21–86
Bacry E, Delour J, Muzy JF (2001) Multifractal random walk. Phys Rev E 64:026103–026107
Baroni M PMA, Wit AD, Rosa RR (2010) Detrended fluctuation analysis of numerical density and viscous fingering patterns. Europhys Lett 92:64002–64008
Cardenas N, Kumar S, Mohanty S (2012) Dynamics of cellular response to hypotonic stimulation revealed by quantitative phase microscopy and multi-fractal detrended fluctuation analysis. Appl Phys Lett 101:203702–203706
Chen Z, Ivanov PC, Hu K, Stanley HE (2002) Effect of nonstationaries on detrended fluctuation analysis. Phys Rev E 65:041107
Efstathiou NM, Tzanis C, Cracknell A, Varotsos CA (2011) New features of land and sea surface temperature anomalies. Int J Remote Sens 32:3231–3238
Eichner JF, Koscielny-Bunde E, Bunde A, Havlin S, Schellnhuber H-J (2003) Power-law persistence and trends in the atmosphere: a detailed study of long temperature records. Phys Rev E 68:046133–046141
Esen F, Cag͂lar S, Ata N, Ulus T, Birdane A, Esen H (2011) Fractal scaling of laser Doppler flowmetry time series in patients with essential hypertension. Microvasc Res 82(3):291–295
Feder J (1988) Fractals. Plenum Press, New York
Hurst HE (1951). Trans Am Soc Civil Eng 116:770–799
Hurst HE, Black RP, Simaika YM (1965) Long-term storage: an experimental study. Constable, London
Ignaccolo M, Latka M, West BJ (2010) Detrended fluctuation analysis of scaling crossover effects. Europhys Lett 90:10009–10015
Jones PD, Parker DE, Osborn TJ, Briffa KR (2013) Global and hemispheric temperature anomalies—land and marine instrumental records. In: Trends: A Compendium of Data on Global Change, Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge. Tenn USA. doi:10.3334/CDIAC/cli.002
Kantelhardta JW, Zschiegnera SA, Koscielny-Bundec E, Havlind S, Bunde A, Stanley HE (2002) Multifractal detrended uctuation analysis of nonstationary time series. Physica A 316:87–114
Kantelhardt JW, Rybski D, Zschiegner SA, Braun P, Koscielny-Bunde E, Livina V, Havlin S, Bunde A (2003) Multifractality of river runo and precipitation: comparison of fluctuation analysis and wavelet methods. Physica A 330:240–245
Koscielny-Bunde E, Kantelhardt JW, Braun P, Bunde A, Havlin S (2006) Long-term persistence and multifractality of river runoff records: Detrended fluctuation studies. J Hydrol 322:120–137
Kwapień J, Oswiecimka P, Drozdz S (2005) Components of multifractality in high-frequency stock returns. Physica A 350:466–474. and the references therein
Liao F, Struck DB, Macrobert M, Jan Y-K (2001) Multifractal analysis of nonlinear complexity of sacral skin blood flow oscillations in older adults. Med Biol Eng 49(8):925–934
Lu X, Tian J, Zhou Y, Li Z (2013) Multifractal detrended fluctuation analysis of the Chinese stock index futures market. Physica A 392:1452–1458
Mali P (2014) Fluctuation of gold price in India versus global consumer price index. Fractals 22(1–2):1450004. 9 pages
Mali P, Mukhopadhyay A (2014) Multifractal characterization of gold market: a multifractal detrended fluctuation analysis. Physica A 413:361–372
Mandelbrot BB (1963) The variation of certain speculative prices. J Bus 36:394–419
Mandelbrot BB (1982) The fractal geometry of nature. WH Freeman and Company, New York
Maraun D, Rust HW, Timmer J (2004) Tempting long-memory—on the interpretation of DFA results. Nonlinear Proc Geoph 11:495–503
Murguia JS, Carlo MM, Ramirez-Torres MT, Rosu HC (2013) Wavelet multifractal detrended fluctuation analysis of encryption and decryption matrices. Int J Mod Phys C 24:1350069–1350082
Peng C-K, Buldyrev SV, Havlin S, Simons M, Stanley HE, Goldberger AL (1994) Mosaic organization of DNA nucleotides. Phys Rev E 49:1685–1689
Samadder S, Ghosh K, Basu T (2013) Fractal analysis of prime Indian stock market indices. Fractals 21:1350003. 12 pages
Schreiber T, Schmitz A (1996) Improved surrogate data for nonlinearity tests. Phys Rev Lett 77:635–638
Theiler J, Eubank S, Longtin A, Galdrikian B, Farmer JD (2092) Testing for nonlinearity in time series: the method of surrogate data. Physica D 58:77–94
Varotsos CA, Milinevsky G, Grystai A, Efstathiou MN, Tzanis C (2008) Scaling effect in planetary waves over Antarctica. Int J Remote Sens 29(9):2697–2704
Varotsos C, Efstathiou M, Tzanis C (2009) Scaling behaviour of the global tropopause. Atmos Chem Phys 9(2):677–683
Varotsos CA, Melnikova I, Efstathiou MN, Tzanis C (2013a) 1/f noise in the UV solar spectral irradiance. Theor Appl Climatol 111(3–4):641–648
Varotsos CA, Efstathiou MN, Cracknell AP (2013b) On the scaling effect in global surface air temperature anomalies. Atmos Chem Phys 13:5243–5253
Veronese TB, Rosa RR, Bolzan MJA, Fernandes FCR, Sawant HS, Karlicky M (2011) Fluctuation analysis of solar radio bursts associated with geoeffective X-class flares. J Atmos Solar-Terr Phys 73:1311–1316
Zhang YX, Qian WY, Yang CB (2008) Multifractal structure of pseudorapidity and azimuthal distributions of the shower particles in Au+Au collisions at 200 A GeV. Int J Mod Phys A 23:2809–2816
Acknowledgments
I thank the anonymous reviewer for his/her careful reading of the manuscript and valuable comments and suggestions which help to improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mali, P. Multifractal characterization of global temperature anomalies. Theor Appl Climatol 121, 641–648 (2015). https://doi.org/10.1007/s00704-014-1268-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00704-014-1268-y