1 Introduction

Hydraulic fracturing behavior of various rocks such as sandstones, shales, granites and even artificial rocks has been widely studied over a period of years. Hydraulic fracturing tests in laboratory are usually carried out under constant injection rate or pressurization rate, and the breakdown pressure observed from the laboratory tests was found to be loading rate dependent. However, there was no consistent conclusion on the rate-dependent influence. Some reported an increase in breakdown pressure with increasing injection or pressurization rate in hydrostone (Haimson and Fairhurst 1969), Weber and Ruhr sandstones (Zoback et al. 1977), granite (Solberg et al. 1980), cement and mortar (Ha et al. 2017) and clay shale (Morgan et al. 2017), while some others reported an opposite finding in tight gas sandstone (Zeng and Roegiers 2002). Solberg et al. (1977) reported there is no difference in breakdown pressures of granite specimens at very slow injection rates of 0.33–3.3 mm3/s. It has been argued that pressurization rate influences the breakdown pressure depending upon whether the rock is permeable or not (Zoback et al. 1977, Detournay and Cheng 1992; Garagash and Detournay 1996). Clearly, the loading rate-dependent phenomena are related to the infiltration of injecting fluids in different rocks. A few studies performed sleeve fracturing tests to exclude hydraulic effects (Ishida et al. 1997; Brenne et al. 2013; Stoeckhert et al. 2015).

Various theoretical models or equations have been presented to predict breakdown pressure of rocks during hydraulic fracturing. Guo et al. (1993) systematically reviewed several typical models including the first breakdown model by Hubbert and Willis (1957), tensile strength model, poroelastic model, shear failure model, point stress model and fracture mechanics model. They concluded that most of the models have their own limitation, and the fracture mechanics model is the most promising one which is possible to explain phenomenon of rate, size, fracture fluid and stress dependent. The main difficulty in predicting breakdown pressure is that injected fluid penetrates into rock matrix and complicates the breakdown process. Stress changes induced by the fluid infiltration in rocks especially in low-permeability rocks and their influence on fractures development have not been fully understood yet.

Pioneering experimental and theoretical work considering penetration of injected fluid during hydraulic fracturing has been conducted by Haimson and Fairhurst (1967, 1969, 1970), Haimson (1968, 1975). The model presented by Haimson and Fairhurst (H–F model) (1967) introduced the Biot’s poroelastic parameter when analyzing stresses in rock. Later Detournay and Cheng (1992) introduced a length-scale parameter around the wellbore in their breakdown model (D–C model) where fluid diffusion along the length was considered. Degue and Ladanyi (2000) also mentioned that the effect of pressurization rate on the breakdown pressure is closely related to the extent of fluid penetration into the cracks. Song and Haimson (2001) modified the D–C model by replacing the Terzaghi’s effective stress with a general effective stress based on experimental results of high-porosity (26%) Tablerock sandstone.

Hydraulic fracturing behavior of different granites has been reported by Haimson (1975, 1999), Haimson and Lee (1980), Solberg et al. (1980), Haimson and Doe (1983), Haimson and Zhao (1991), Zhao et al. (1996), Ishida et al. (1997, 2000, 2004, 2012) and Chen et al. (2015). However, in these studies granites were mainly treated as low-permeability rocks and the influence of infiltration of injection fluid has rarely been discussed. Moreover, there is anisotropy phenomenon in some granites and they have three cleavages or planes of weakness called rift, grain and hardway (Douglass and Voight 1969; Fujii et al. 2007). The cleavages have different tensile strength and permeability and therefore influence fracture generation in laboratory hydraulic fracturing test (Chen et al. 2015; Zhuang et al. 2016a; Diaz et al. 2016).

Geometrical properties including the aperture of induced fractures are very important for deep geothermal energy development in crystalline rocks. For measurement of the aperture of fractures, X-ray computed tomography (CT) as a nondestructive method was often used (Johns et al. 1993; Keller 1997; Bertels et al. 2001; Zhuang et al. 2016a). This method can help to analyze geometric properties of induced fractures as well as fracture propagation (Renard et al. 2009; Jia et al. 2013; Li et al. 2017). Large apertures can be measured directly by counting the number of pixels across the fracture width while measurement on small apertures less than 1 pixel requires a special approach (Keller 1997).

In this study, hydraulic fracturing and sleeve fracturing tests on granite samples were both performed under seven different injection rates and test results were compared to clarify the influence of water infiltration. X-ray computed tomography (CT) was applied to analyze preexisting microcracks and induced fractures in granite specimens.

2 Experimental Setup

2.1 Test Equipment

We developed a hydraulic fracturing test equipment for core-scale samples (Fig. 1). One chamber covered the testing section around the specimen to apply hydrostatic pressure on test specimen. The specimen was connected to the top and bottom nozzle plates. O-rings were installed inside nozzle plates to prevent water and pressure leakage. A membrane was placed around the specimen, and therefore, it was isolated from oil in the chamber in case of a confining pressure being applied. Fluid was injected into specimen from the bottom at a constant injection rate or pressurization rate through a servo-controlled injecting system. The maximum injection pressure is 35 MPa, and the maximum confining pressure is 20 MPa. Four pressure sensors were installed. Two of them were used to measure injection fluid pressures near the specimen and near the booster, and the other two were used to measure confining pressure in the cell and vertical pressure in the upper chamber. Displacement of booster was measured by a LVDT (linear variable differential transformer), and therefore, injection rate can be estimated based on the displacement per unit time and the cross-sectional area of the booster.

Fig. 1
figure 1

Schematic diagram of the hydraulic fracturing test system: a overview and b details around the specimen. Linear variable displacement transducer (LVDT)

Full size image

2.2 Rock Sample

Test material was Pocheon granite taken from Pocheon area in Korea. X-ray diffraction analysis shows that the granite is largely composed of albite (35.9%), quartz (35.7%), microcline (25.8%) and biotite (2.6%). The average measured effective porosity is 0.66%. The Pocheon granite shows mild but clear anisotropy with three typical cleavages of rift (R), grain (G) and hardway (H). The measured average grain size is 0.94 mm in rift plane, 1.01 mm in grain plane and 0.91 mm in hardway plane. Among the three planes, rift plane has the highest microcrack density and therefore its tensile strength is the lowest, whereas the hardway plane has the lowest microcrack density and the highest tensile strength (Park et al. 2004; Zhuang et al. 2016b). Figure 2a, b shows microcracks in a thin section of Pocheon granite cut parallel to the rift plane. Both of intergranular and transgranular microcracks exist, and most of these microcracks were found in quartz grains. Park et al. (2004) reported that the preferred orientation of transgranular microcracks in the quartz is approximately parallel to the rift plane. Figure 2c, d shows a very small granite sample with diameter of 5 mm and a three-dimensional CT image of microcracks extracted from the sample with the voxel pitch of 8 μm. It is observed that each microcrack is a plane and some planes connect in the three-dimensional spatial distribution.

Fig. 2
figure 2

Preexisting microcracks in granite. a, b Thin sections of Pocheon granite cut parallel to the rift plane. Major microcracks were found in quartz grains. Qz quartz, Mc microcline, Pl plagioclase, Prt perthite, c a mini granite sample with diameter of 5 mm and d 3D spatial distribution of microcracks, the colors represent different microcracks

Full size image

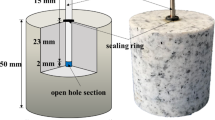
Granite specimens were cored in directions perpendicular to the three cleavage planes, and their basic physical and mechanical properties were measured. Table 1 lists main measured results. Elastic modulus was measured on cylinders having diameters of 50 mm and lengths of 200 mm. Brazilian tensile strength (BTS) was measured with disks having diameters of 50 mm and thicknesses of 25 mm, and the loading direction was parallel to the rift, grain and hardway plane, respectively. Uniaxial compressive strength (UCS) was measured with cylinders having diameters of 50 mm and heights of 100 mm. Hydraulic conductivity was measured with cylinders having diameters of 50 mm and heights of 50 mm at a water temperature of 15 °C and a constant water head pressure of 0.1 MPa. Figure 3 shows the three typical specimens used in fracturing tests, and they were labeled with R, G and H, respectively. Each specimen is 50 mm in diameter and 100 mm high. The diameter of a through-going borehole in the center of specimen is around 8 mm.

Table 1 Main physical and mechanical parameters of Pocheon granite
Full size table
Fig. 3
figure 3

Granite specimens cored in directions perpendicular to the rift, grain and hardway planes. Ø borehole diameter, D sample diameter, H sample height

Full size image

2.3 Test Conditions

The confining pressure was selected to be zero for all of the tests in this study, and the influence of confining pressure is not considered. The vertical pressure was fixed to be around 25 MPa to make sure of safe sealing and no leakage from the top and bottom surfaces of specimen connecting with nozzle plates. Due to the above stress conditions, vertical tensile hydraulic fractures will be induced in the samples.

Hydraulic fracturing tests used H and R specimens. G specimen was not used because it was tested to have similar hydraulic fracturing behavior with H specimen because they have the same weak plane of the rift in radial direction. Injection rate was constant in each test, and seven different injection rates were used (q = 1, 5, 10, 25, 50, 75, and 100 mm3/s). The highest injection rates were chosen referring to past studies using similarly sized specimens (Solberg et al. 1980; Brenne et al. 2013). Sleeve fracturing tests were performed on H specimens for comparison with hydraulic fracturing tests. The borehole, top surface and bottom surface were sleeved with a latex cover to prevent water infiltration. The main test conditions are summarized in Tables 2 and 3. Moreover, injection tests without fracturing were performed on additional granite specimens to measure how much water infiltrates into specimen at different injection time and injection pressures.

Table 2 Test conditions and main results of hydraulic fracturing tests
Full size table
Table 3 Test conditions and main results of sleeve fracturing tests
Full size table

3 Experimental Results and Analysis

3.1 Influence of Injection Rate

Figure 4 plots injection pressure with respect to total injected volume of H specimens under the seven different injection rates from 1 to 100 mm3/s. The volume is calculated as the injection rate (q) multiplied by injection time (t). The x-axis gives the total injected volume instead of injection time because the total injection time spent at the end of test for the lowest and the highest injection rate are very different and it is difficult to view each result clearly in the same scale of time. It should be noted that the total injected volume does not mean the volume of water infiltrating into specimen, as some water discharged through outside surface of cylinder. The beginning section of each curve shows a slow increase in injection pressure because there was air remained in the booster, which delayed compression of the water to provide pressure.

Fig. 4
figure 4

Injection pressure plotted with respect to total pumped volume at different injection rates for H specimens. The total pumped volume was estimated by multiplying the pumping time t by the injection rate q

Full size image

Two types of curve pattern are observed in the figure. The first type presents at low injection rates from 1 to 25 mm3/s. Injection pressure increased slowly with increasing injected volume and then converged to a certain value, which is defined as the maximum injection pressure Pmax. A peak injection pressure was not observed, which indicates that the specimen was not hydrofractured. The second type presents at high injection rates from 50 to 100 mm3/s. Injection pressure increased faster compared to those at low injection rates and reached a peak called breakdown pressure (Pb). After the peak, injection pressure dropped very quickly to zero because the confining pressure was zero. For both types of curves, the ascending section was not linear especially when approaching Pmax or Pb.

3.2 Measurement of Water Infiltration

To explain the two types of injection pressure variation and also to further investigate the effect of water infiltration, additional injection tests were performed to measure the weight of water infiltrated into granite specimen at different time and different resultant injection pressures. To avoid any influence of water injection, each specimen was used only once. Specimens were completely dried and weighed before testing. Water was injected at a constant injection rate and injection was stopped when the injection pressure reached a certain value. The specimen was removed and weighed again. The remained water adhered to the surface and borehole was blown off with a drier. The difference between the initial weight and the weight after testing is attributed to the weight of water infiltrated into the specimen during injection. The total volume of interconnected pores was estimated as the average effective porosity (0.66%) multiplied by the volume of the specimen. The ratio of volume of infiltrated water and the total volume of pores is defined as degree of saturation.

Figure 5a, b compares variations of injection pressure and degree of saturation at a low injection rate of 1 mm3/s and a high injection rate of 100 mm3/s. At the low injection rate of 1 mm3/s, the specimen reached full saturation after 2000 s while the injection pressure was only 0.45 MPa. Given that the specimen was saturated, inflow and outflow reach equilibrium and injection pressure will not increase any more. As a result, specimen was not hydrofractured. At the high injection rate of 100 mm3/s, degree of saturation was < 80% while the injection pressure almost reached the breakdown pressure, meaning that specimen was fractured before it was fully saturated. In the same way, for injection tests at low injection rates of 10 and 25 mm3/s, the maximum injection pressures were only 2.06 and 5.06 MPa as full saturation is approached. As a result, the specimens were not hydrofractured because the injection pressures are much lower than the threshold breakdown pressure (around 6.0 MPa). At the injection rate of 50 mm3/s, breakdown was achieved at a degree of saturation around 80%.

Fig. 5
figure 5

Injection pressure and degree of saturation with respect to injection time. a Injection rate q = 1 mm3/s and bq = 100 mm3/s. Pmax is the maximum injection pressure at the end of each injection test

Full size image

3.3 Influence of Rock Anisotropy

Granite shows mild but clear anisotropy along three typical cleavage planes with different microcrack densities and thus with different tensile strength and hydraulic conductivities. The anisotropy therefore influences hydraulic fracturing behavior. Figure 6a, b compares typical injection pressure–time curves of H and R specimens at constant injection rates of 25 and 50 mm3/s, respectively. At the lower injection rate of 25 mm3/s, there was no breakdown for H specimen while breakdown occurred at 7.17 MPa for R specimen. When the injection rate was increased to 50 mm3/s, breakdown occurred in both R and H specimens with Pb of 8.14 and 6.00 MPa, respectively. These values are very close to the average BTS of rift plane and grain plane, which are 8.20 and 6.05 MPa. Under the stress conditions used here, tensile fractures will be generated in vertical direction. As a result, induced fractures will be along grain plane for R specimens, while they are along rift plane for H specimens. Therefore, it is confirmed that the difference in breakdown pressures comes from the difference in tensile strength between rift plane and grain plane.

Fig. 6
figure 6

Comparison of injection pressure–time curves for H and R specimens at injection rate of aq = 25 mm3/s and bq = 50 mm3/s

Full size image

Moreover, injection pressure developed more quickly in R specimens than that in H specimens, probably due to the influence of water infiltration along different permeability of media. As the specimens are hollow cylinders, water will mainly infiltrate radially outward from borehole. Each microcrack in granite represents a long narrow pore or a path available for water infiltration. The H specimens have two weak planes (rift and grain) in radial direction. Water will infiltrate into the rift plane faster compared to other directions because of its highest microcrack density, giving it the highest permeability. The R specimens, with grain and hardway planes in the radial direction, will have water mainly infiltrating in the grain plane or the hardway plane as the two have no significant difference in hydraulic conductivity. Overall, water infiltration speed will be the fastest when it occurs along the rift plane rather than the grain or hardway plane. As a result, at a given injection rate, injection pressure in H specimens developed more slowly than that in R specimens because of higher infiltration speed and greater water loss along the rift plane.

3.4 Sleeve Fracturing Test Results and Comparison

To exclude the influence of water infiltration, a set of sleeve fracturing tests as listed in Table 3 were performed on H specimens for comparison with hydraulic fracturing tests. Figure 7 shows comparisons of injection pressure–total injected volume curves at different injection rates of 1, 10, 50 and 100 mm3/s, respectively. Breakdown was observed in sleeve fracturing tests at both low and high injection rates. Ignoring the beginning part, injection pressure increased almost linearly until breakdown regardless of injection rate. Moreover, injection pressures developed much quicker in sleeve fracturing tests because there is no water loss during injection.

Fig. 7
figure 7

Comparison of injection pressure variation between tests with and without sleeve

Full size image

3.5 Comparison of Breakdown Pressures

Figure 8 compares breakdown pressure Pb in the three sets of tests. Generally, Pb increases approximately linearly with increasing injection rate regardless of specimen or sleeve condition. In hydraulic fracturing tests, there is a threshold injection rate to induce breakdown, and this is expected to be between 25 and 50 mm3/s for H specimens and between 10 and 25 mm3/s for R specimens under the applied stress conditions in this study. The breakdown pressures for both H specimen and R specimen at the threshold injection rate are very similar to the average BTS of the cleavage planes where fractures were generated. However, it is still difficult to conclude that the BTS can well predict breakdown pressure because breakdown pressure is still influenced by many other parameters, e.g., specimen size and borehole size. Guo et al. (1993) noted that the BTS predicts too low a breakdown pressure. Experimental results by Brenne et al. (2013) also show the inconsistency between the two for six types of rocks; particularly, the BTS of sandstone underestimated the breakdown pressures regardless of borehole size.

Fig. 8
figure 8

Comparison of breakdown pressures under different test conditions. SF sleeve fracturing, HF hydraulic fracturing

Full size image

The Pb of H specimens in sleeve fracturing ranges around 18–23 MPa, which are more than two times higher than those in hydraulic fracturing. The classical breakdown prediction models mainly considering in situ stresses, tensile strength and pore pressure effect are not able to predict the anomalously high Pb. This phenomenon was also pointed out by Brenne et al. (2013), and they used the fracture mechanics model to explain the quite high breakdown pressures in sleeve fracturing test by assuming presence of cracks with relatively large length.

The granite specimen was split in two in all of sleeve fracturing tests by direct observation, while the induced fractures in hydraulic fracturing tests were usually along one side and in most cases fracture height was smaller than the specimen height based on CT observations. From the viewpoint of energy consumption, the energy released by sleeve fracturing must be higher, indicating a higher external work by the injection pressure. Figure 9 shows a typical example of injection pressure variation together with amplitude of induced acoustic emission (AE) hits detected during hydraulic fracturing test of H specimen at an injection rate of 100 mm3/s. It is found that induced AE hits started at an injection pressure of near 7.0 MPa, which is very close to the BTS of rift plane of granite specimen. This indicated that cracks have likely been generated near borehole along rift plane when the injection pressure exceeds its tensile strength. However, with sleeve around borehole, there is no water leaking into specimen and fluid pressure is not able to reach inside of the initial cracks to promote fracture propagation. Therefore, there is no decrease in injection pressure increment. Injection pressure continued to increase linearly because of the confined space of borehole until the specimen was totally fractured or the specimen failed. The resulted breakdown pressure is influenced by the stress gradient in the sample, which is specimen size dependent.

Fig. 9
figure 9

Acoustic emission measurements in sleeve fracturing test at q = 100 mm3/s

Full size image

4 Analysis of Pressurization Rate Change

Pressurization rate is the variation of injection pressure per unit time. It is influenced by both specimen and injection rate. The typical injection pressure–time curve in hydraulic fracturing tests can be divided into a linear section and a nonlinear section ignoring the very beginning section. The slope of the linear section is noted as resultant pressurization rate, and its estimated value under each test condition is given in Tables 2 and 3. For both hydraulic and sleeve fracturing tests, the resultant pressurization rate increases with increasing injection rate, but not in a linear fashion, especially in hydraulic fracturing tests. The resultant pressurization rates in sleeve fracturing tests are obviously much higher than those in hydraulic fracturing test.

The nonlinear section starting from a point where injection pressure deviates from the linear approximation to the point where injection pressure starts to decrease or converges is fitted by a quadratic polynomial, and dP/dt was calculated through time integration. To distinguish it from the resultant pressurization rate estimated from the linear section, dP/dt is defined as “pressurization increment.”

Figure 10 plots the pressurization increment with respect to injection pressure for H specimens at different injection rates of 10–100 mm3/s. For hydraulic fracturing tests, the pressurization increment initially decreases almost linearly with increasing injection pressure regardless of injection rate. It then deviates from the linear approximation at a certain point, Pi. Magnitude of the injection pressure at point Pi is noted beside each curve. The ratio of Pi and the maximum injection pressure Pmax or Pb is around 78–89%. The pressurization increment decreases due to loss of injection fluid, as the inflow is constant (because injection rate is constant) while outflow increases. dP/dt reduces to almost zero when the inflow and outflow are balanced. When water infiltration is ignored in sleeve fracturing tests, injection pressure–time curve is almost linear and pressurization rate is nearly constant until the breakdown.

Fig. 10
figure 10

Pressurization increment dP/dt with respect to injection pressure at different injection rates for H specimens in hydraulic and sleeve fracturing tests. Pi is the injection pressure at which pressurization rate deviates from the linear approximation

Full size image

A similar phenomenon has been reported by Song and Haimson (2000, 2001), who found two different types of dP/dt variation with injection pressure in Berea sandstone and Tablerock sandstone having high porosities of 17–25 and 26.0%, respectively. When the injection rate was too low to pressurize the wellbore for hydrofracking, dP/dt linearly decreased with increasing injection pressure all the way to zero, while for a high injection rate, dP/dt showed a linear decrease at first and then it deviated from the linear approximation and became even faster slow down at a certain point. The point was defined as the “apparent breakdown pressure,” where permeability suddenly changes due to tensile fracturing.

However, unlike Tablerock sandstone, granite showed a nonlinear variation of pressurization increment at both low and high injection rates. This is probably due to differences in pore structures between the porous sandstones and the low-permeability granite. Zimmerman (1991) noted that the pore compressibility of any non-circular pore must be greater than that of a circular pore. There are many thin and long microcracks in granite, and they could open even with a small injection pressure. This could result in dilation of granite specimen and permeability increase from an early stage of injection. Song et al. (2004) found that the permeability of Westerly granite increases with decreasing effective pressure hence increasing pore pressure. The pores in the two sandstones are much less compressible and show negligible deformation at the early pressure stage. The permeability of the sandstones changed at the late stage owing to induced fractures.

5 X-ray CT Observations on Induced Fractures

After the hydraulic fracturing test specimen was removed. CT scan was then performed on the specimen to observe internal changes, particularly induced fractures. Figures 10 and 11 show typical two-dimensional CT images of cross sections of H and R specimens after testing. The resolution is 0.0569 mm/pixel.

Fig. 11
figure 11

Comparison of induced fractures in H specimens at various injection rates aq = 50 mm3/s, bq = 75 mm3/s and cq = 100 mm3/s

Full size image

Figure 11a–c compares the induced fractures in H specimens at different injection rate of q = 50, 75 and 100 mm3/s, respectively. Figure 12a–d compares the induced fractures in R specimens at different injection rate of q = 25, 50, 75 and 100 mm3/s, respectively. It is confirmed that fractures are along the rift plane for H specimens and they are along the grain plane for R specimens. In most cases, fractures are located on one side rather than being symmetrically distributed around the borehole. The main reasons for the result are that the borehole is not exactly in the center of specimen and the granite specimen is heterogeneous and anisotropic. Moreover, in most cases fractures were generated only in the upper part or the lower part of specimen, which means the height of fractures is usually smaller than the height of specimen.

Fig. 12
figure 12

Comparison of induced fractures in R specimens at various injection rates aq = 25 mm3/s, bq = 50 mm3/s, cq = 75 mm3/s and dq = 100 mm3/s

Full size image

Note that one H specimen showed no peak in the pressure–time curves at q = 25 mm3/s, indicating the absence of breakdown. However, a few very thin fractures with aperture < 1 pixel were observed in enlarged image of the specimen. At low injection rates and relative low injection pressures compared to the breakdown pressure, water slowly infiltrates granite specimen. It is likely that preexisting microcracks in granite opened and extended and further connected each other to form longer cracks.

The aperture of induced fractures was roughly measured by enlarging the CT images in the open source software of ImageJ (Ferreira and Rasband 2012) and counting the number of pixels along the direction of fracture width based on the intensity values of pixels, as the intensity values of pixels indicating the induced fracture, which is empty space, is much lower than those of pixels indicating the granite. The accuracy was limited to 1 pixel. The maximum aperture of fractures was decided by comparing measurements in different slices corresponding to different heights of the specimen. Table 2 lists the results of the maximum aperture of fractures under different test conditions. Generally, the aperture increases with increasing injection rate or increasing breakdown pressure. Moreover, at the same injection rate in hydraulic fracturing tests, the R specimens showed apertures 1–3 pixels larger than those in the H specimens. This is because the breakdown pressures were higher in the R specimens.

The fractures were extracted to show their 3D geometries and apertures. Figure 13a–d compares four typical cases of two H specimens and two R specimens with injection rates of 50 and 100 mm3/s, respectively. Coincidentally, the two cases at q = 50 mm3/s show clear fracture branching. One started from the borehole, while the other started in the middle of specimen. It is highly likely that the two branching are both related to quartz clusters inside the specimen. The quartz grains have abundance of microcracks, which can be classified into intragranular, intergranular and boundary ones (Diaz et al. 2016). These different types of microcracks influence how fractures were generated. Further study is needed in this regard. Tortuosity, which is defined as the ratio of the total length of a fracture and the distance between its two ends, was measured on the main fractures ignoring the branching. The four cases in Fig. 13a–d gave a result of 1.055, 1.056, 1.044 and 1.056, respectively. There is almost no difference among the values.

Fig. 13
figure 13

Extraction of main fractures show 3D geometry and front view aq = 50 mm3/s, H specimen, bq = 50 mm3/s, R specimen, cq = 100 mm3/s, H specimen and dq = 100 mm3/s, R specimen

Full size image

Figure 14 shows typical images of induced fractures in sleeve fracturing tests at injection rates of 50 and 100 mm3/s. Specimens were split in two and the fracturing was accompanied by a clearly audible sound, indicating high energy release. Preliminary acoustic emission measurement showed that the maximum acoustic amplitudes detected in sleeve fracturing test was around 80 dB on average which is 1.1–1.3 times higher than those in hydraulic fracturing tests under the same injection rate of 100 mm3/s. Moreover, the induced fractures in sleeve fracturing tests appear to be straighter with less branching than those in hydraulic fracturing tests. The measured tortuosity is 1.049 for q = 50 mm3/s and 1.038 for q = 100 mm3/s. There is only tiny difference between tortuosities of hydraulic and sleeve fracturing tests probably due to a limited size of specimen.

Fig. 14
figure 14

Induced fractures in sleeve fracturing tests at injection rates of aq = 50 mm3/s and bq = 100 mm3/s

Full size image

6 Discussions

Pocheon granite is generally considered impermeable due to its very low permeability. However, many long and partially connected microcracks exist inside granite especially in the three cleavage planes of rift, grain and hardway. Injected fluid can infiltrate the rock matrix and open these microcracks under the action of injection pressure. Comparisons of hydraulic and sleeve fracturing test results showed that water infiltration significantly influences hydraulic fracturing behavior of granite. Three important things arise from the test results and require further discussion.

  1. 1.

    Hydraulic fracturing behavior of granite is different from that of other rocks such as sandstone due to abundant preexisting natural microcracks inside granite. This implies that water infiltration influence is different for different pore structures in rocks. However, Zoback and Byerlee (1975) noted that though microcracks dilatancy has influences on permeability of Westerly granite specimens in laboratory, the magnitude of permeability contributed by microcracks measured in laboratory is much less than that of in situ conditions. Dilatancy and fluid flow occur on the scale of joints and fractures in field scale. Nevertheless, the finding on the effect of microcracks can be a reference for studying influence of large scale natural fractures.

  2. 2.

    Although granite shows mild anisotropy due to existing of the three cleavages compared to sedimentary rocks, the influence of the anisotropy on hydraulic fracturing behavior was clearly confirmed at a core scale. However, when it comes to the field scale with complex geological structures which were not able to be reflected by core-scale samples in laboratory, the anisotropy effect may not be as prominent as in the laboratory scale. For example, Duevel and Haimson (1997) noted that the pink Lac du Bonnet granite is practically isotropic in compression despite that its tensile strength and tensile modulus show stronger anisotropy. The influence of anisotropy in Pocheon granite will be further investigated on larger samples considering in situ stresses.

  3. 3.

    The estimation of pressurization increment inferred that some local damages (cracks or fractures) inside specimen may have already happened at around 78‒89% of the maximum injection pressure or the breakdown pressure. Therefore, we anticipate that a specimen is likely to achieve breakdown at a relatively lower injection pressure through cyclic injection (Zhuang et al. 2016a, 2017). This might reduce the induced seismicity during hydraulic stimulation, as preliminary experimental results show that the maximum amplitude of induced AE was reduced by cyclic injection with lowered injection pressure (Zhuang et al. 2017). Further study is needed in this field.

Note that all of the test results in this study are limited to the condition of zero confining pressure. Confining pressure, shear stresses as well as other factors such as temperature will influence permeability of granite samples (Morrow et al. 1986; Song et al. 2004; Alam et al. 2015). As a result, water infiltration varies at different in situ conditions. In this study, the stress condition was set to be very simple and ideal. Fluid infiltration and induced fracture mainly happened along the weak planes with a number of microcracks. When considering in situ stresses and natural fractures for field application, fluid infiltration will become more complex. From this respect, the experimental findings in the laboratory have to be used as basic study for application of hydraulic fracturing that will occur in a more complex manner in field.

7 Conclusions

A series of hydraulic and sleeve fracturing tests were performed on granite specimens taking into account anisotropy. Effect of injection rate varying from 1 to 100 mm3/s was investigated. Injection pressure–time curves were classified into two types with and without fracturing corresponding to low and high injection rates.

  1. 1.

    The maximum injection pressure or the breakdown pressure increases with increasing injection rate. There is a threshold injection rate in hydraulic fracturing tests at which breakdown can be induced. Injection rates below the threshold caused the injection pressure to develop too slowly to break the granite specimen. Injection pressure stops increasing when the specimen reaches a saturation state at which inflow equals outflow. If the injection rate is too high, injection pressure develops quickly and there is no enough time for water to fully infiltrate the specimen. In such a case, specimen failed at a relatively high breakdown pressure.

  2. 2.

    Hydraulic fracturing behavior of granite is quite different from sleeve fracturing where water infiltration is excluded. Injection pressure develops nonlinearly in hydraulic fracturing tests before reaching the maximum value, while it develops approximately linearly in sleeve fracturing tests. Without confining pressure, the breakdown pressures in hydraulic fracturing are similar to the BTS, while they are more than two times higher than the BTS in sleeve fracturing.

  3. 3.

    Cleavage anisotropy has influence on the orientation of generated fractures. Induced fractures are mainly along rift plane for H specimens and they are along grain plane for R specimens. The difference of breakdown pressures between the two specimens compared at the same injection rate is very close to the difference in the BTS between rift plane and grain plane.

  4. 4.

    X-ray CT observations show that the maximum aperture of induced fractures increases with increasing breakdown pressure in hydraulic fracturing test. Tortuosities of generated fractures were measured to be around 1.04–1.06. There is no obvious difference among different test conditions. The limited specimen size could be one important reason.