Abstract
Time dependency in tunnel excavation is mainly due to the rheological properties of rock and sequential excavation. In this paper, analytical solutions for deeply buried tunnels with elliptical cross-section excavated in linear viscoelastic media are derived accounting for the process of sequential excavation. For this purpose, an extension of the principle of correspondence to solid media with time varying boundaries is formulated for the first time. An initial anisotropic stress field is assumed. To simulate realistically the process of tunnel excavation, solutions are developed for a time-dependent excavation process with the major and minor axes of the elliptical tunnel changing from zero until a final value according to time-dependent functions specified by the designers. In the paper, analytical expressions in integral form are obtained assuming the incompressible generalized Kelvin viscoelastic model for the rheology of the rock mass, with Maxwell and Kelvin models solved as particular cases. An extensive parametric analysis is then performed to investigate the effects of various excavation methods and excavation rates. Also the distribution of displacements and stresses in space at different times is illustrated. Several dimensionless charts for ease of use of practitioners are provided.
Similar content being viewed by others
1 Introduction
Analytical solutions are invaluable to gather understanding of the physical generation of deformations and stresses taking place during the excavation of tunnels. Closed-form solutions allow highlighting the fundamental relationships existing between the variables and parameters of the problem at hand, for instance between applied stresses and ground displacements. Moreover, although numerical methods such as finite element, finite difference and to a lesser extent boundary element are increasingly used in tunnel design, full 3D analyses for extended longitudinal portions of a tunnel still require long runtimes, so that the conceptual phase of the design process relies on 2D analytical models. In fact, analytical solutions allow performing parametric sensitivity analyses for a wide range of values of the design parameters so that preliminary estimates of the parameters to be used in the successive phases of the design process can be obtained. In addition, they provide a benchmark against which the overall correctness of sophisticated numerical analyses, performed in the final design stage, can be assessed.
Most types of rocks, whether hard or soft, exhibit time-dependent behaviors (Malan 2002), which induce gradual deformations over time even after completion of the tunnel excavation process. Elastic and elastoplastic models ignore the effect of time dependency which may contribute up to 70 % of the total deformation (Sulem et al. 1987a). In case of sequential excavation, the observed time-dependent convergence is also a function of the interaction between the prescribed excavation steps and the natural rock rheology. Therefore, proper simulation of the whole sequence of excavation is of great importance for the determination of the optimal values of the tunneling parameters to achieve optimal design (Tonon 2010; Sharifzadeh et al. 2012). Sequential excavation is a technique becoming increasingly popular for the excavation of tunnels large cross-section in several countries (Tonon 2010; Miura et al. 2003). For instance, 200 km of tunnels along the new Tomei and Meishin expressways in Japan, were built via the so-called center drift advanced method. This sequential excavation technique has been adopted by the Japanese authorities “as the standard excavation method of mountain tunnel” (Miura 2003).
In this paper, the rock rheology is accounted for by linear viscoelasticity. The so-called generalized Kelvin, Maxwell and Kelvin rheological models according to the classical terminology used in rock mechanics (Jaeger et al. 2007) will be considered. Unlike the case of linear elastic materials with constitutive equations in the form of algebraic equations, linear viscoelastic materials have their constitutive relations expressed by a set of operator equations. In general, it is very difficult to obtain analytical solutions for most of the viscoelastic problems, especially in case of time-dependent boundaries, although some closed-form solutions have been developed (Brady and Brown 1985; Gnirk and Johnson 1964; Ladanyi and Gill 1984). However, in all these works, only tunnels with circular cross-section are considered, with the excavation being assumed to take place instantaneously. In the literature, the process of sequential excavation is usually ignored since it prevents the use of the principle of correspondence which has been traditionally restricted to solid bodies with time-invariant geometrical boundaries (Lee 1955; Christensen 1982; Gurtin and Sternberg 1962). However, recently, analytical methods have been introduced to obtain analytical solutions for circulars tunnels excavated in viscoelastic rock accounting for sequential excavation (Wang and Nie 2010, 2011; Wang et al. 2013, 2014). But for tunnels of complex cross-sectional geometries, (e.g., elliptic, rectangular, semi-circular, inverted U-shaped, circular with a notch, etc.), analytical solutions are available only in case of elastic medium (Lei et al. 2001; Exadaktylos and Stavropoulou 2002; Exadaktylos et al. 2003), hence disregarding the influence of the time-dependent rheological behavior of the rock and sequential excavation. In this paper instead, an analytical solution is derived for sequentially excavated tunnels of non-circular (elliptical) cross-section in linearly viscoelastic rock subject to a non-uniform initial stress state. The stress field considered is anisotropic so that complex geological conditions can be accounted for. The solution is achieved employing complex variable theory and the Laplace transform.
Elliptical and horse-shoe sections with the longer axis in the vertical direction are rather common for railway tunnels (Steiner 1996; Amberg 1983; Anagnostou and Ehrbar 2013) and caverns in rock, e.g., the East Side Access Project in New York (Wone et al. 2003). Sequential excavation is employed for these types of sections much more often than for circular sections since tunnel boring machine excavation is not available for non-circular sections. Also subway tunnels are often featured by elliptical or horse-shoe cross-sections (Hochmuth et al. 1987). Moreover, several road tunnels require an elliptical or nearly elliptical cross-section with the longer axis in the horizontal direction to minimize the excavation volume whilst meeting the geometrical constraints required for the construction of the road and related walk-ways (Miura et al. 2003). In Japan, elliptical sections are specifically prescribed for mountainous regions (Miura 2003).
A limitation of the analytical solutions here proposed is due to the absence of lining in the cross-section considered. The presence of lining makes the problem mathematically intractable due to the consequent structure–ground interaction. Also in case of non-circular cross-sections, the confinement convergence method cannot be applied due to the anisotropy of the displacement field. Till now, even for the fix-boundary viscoelastic problem, no solutions are proposed for non-circular tunnel with liner in the references. However, the analytical solutions here introduced can be employed to predict tunnel convergence to assess whether the presence of a lining would be necessary in the preliminary design phase. Also, they allow obtaining a first estimate of the magnitude of the excavation-induced displacement field before installation of linings. Moreover, they stand for some tunnels in hard rocks where lining may be unnecessary or is just installed for additional safety with no pressure applied on the lining.
In the paper, analytical solutions are provided for a generic time-dependent excavation process with the major and minor axes of the cross-section increasing monotonically over time according to a function to be specified by the designers. The analytical solutions have been derived in integral form for the case of a generalized Kelvin viscoelastic rock. The case of Maxwell and Kelvin models can be obtained as particular cases of the solution obtained for the generalized Kelvin model. To calculate the displacement and stress fields, numerical integration of the analytical expressions in integral form has been carried out. Then, a parametric study investigating the influence of various excavation methods, as well as excavation rates, on the excavation-induced displacements and stresses is illustrated. Several dimensionless charts of results are plotted for the ease of use of practitioners.
2 Formulation of the Problem
The present study focuses on the excavation of an elliptical tunnel in a rheological rock mass. In the analysis, the following assumptions were made:
-
1.
The rock mass is considered to consist of homogeneous, isotropic, and linearly viscoelastic material under isothermal conditions.
-
2.
The initial stress field in the rock mass is idealized as made of a vertical stress \( p_{0} \) and horizontal stress \( \lambda p_{0} \), where \( \lambda \) is a prescribed ratio, as shown in Fig. 1a.
-
3.
The tunnel is deeply buried, hence no linear variation of the stresses with depth is considered.
-
4.
The excavation speed is low enough that no dynamic stresses are ever induced so that stress changes occur in a quasi-static fashion at all times.
-
5.
The cross-section of the tunnel is sequentially excavated, that is, the half major and minor axes of the elliptical tunnel section, a and b, respectively, are time dependent. The tunneling process may be divided into two stages: the first (i.e., excavation) stage, spans from time \( t = 0 \) to \( t = t_{1} \), with t 1 being the end time of the cross-section excavation whilst the second stage runs from \( t = t_{1} \) onwards. In the first stage, the size of the half major and minor axes varies according to the time-dependent functions, a(t) and b(t), respectively, that are likely to be discontinuous over time due to technological requirements since sequential excavations tend to occur step-like. So, an important feature of the analytical solutions provided in this paper is that they are applicable to any type of sequential excavations either stepwise or continuous over time. Note that in case the ratio of the ellipse axes remains constant, the section grows homothetically; whereas if the ratio changes over time, the shape of the section evolves too (for instance from an initial circular pilot tunnel to a final elliptical section). Since in most of the cases the shape of the cross-section changes over time, the general case of \( d(t) = a(t)/b(t) \) will be considered. The second stage spans from \( t = t_{1} \) onwards, with the values of the half major and minor elliptical axes being equal to a(\( t \ge t_{1} \)) = \( a_{1} \) and b(\( t \ge t_{1} \)) = \( b_{1} \), respectively.
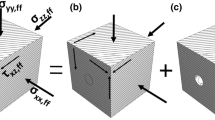
In the analysis, the effect of the advancement of the tunnel along the longitudinal direction is not accounted for. The effect of tunnel advancement can easily be considered employing a fictitious pressure as shown in (Sulem et al. 1987b; Wang et al. 2014), but it is here omitted for sake of simplicity in the derivation of the solution. So the cross-section considered in the analysis is located at a sufficient distance from the tunnel face that stresses and strains are unaffected by three-dimensional effects. According to the aforementioned assumptions, the problem can be formulated as plane strain in the plane of the considered tunnel cross-section. This plane will be assumed to be of infinite size, with an internal elliptical hole growing over time, subject to a uniform anisotropic stress field, and made of a viscoelastic medium. Since the hole is not circular, polar coordinates are no longer advantageous for the derivation of the analytical solution. Hence, in this paper Cartesian coordinates (x, y) are employed for the derivation of the solution (see Fig. 1a) which are then transformed into polar coordinates \( (\rho ,\;\theta ) \) to show that the (already known) solution for a circular cross-section can be obtained as a particular case. A system of local coordinates \( (n_{\chi } ,\;n_{\tau } ) \) is also employed in the paper, with \( n_{\chi } \) and \( n_{\tau } \) being the normal and tangential directions, respectively, along the elliptical boundary (see Fig. 1a). In the following analysis, sign convention is defined as positive for tension and negative for compression.
3 Derivation of the Analytical Solution
To find analytical solutions for boundary value problems of linear viscoelasticity, the most widely used methods are based on the Laplace transform of the differential and boundary condition equations governing the problem, which, in this case, are time-dependent due to the fact that sequential excavation is accounted for. Lee (1955) presents the classical form of the correspondence principle between linear elastic and linear viscoelastic solutions for boundary value problems. The principle establishes a correspondence between a viscoelastic solid and an associated fictitious elastic solid of the same geometry. But until now, this method has been applied only to solid bodies with time-invariant boundaries because when boundaries are functions of time, the boundary conditions cannot be Laplace transformed. In this section, we describe an extension of the principle to time varying stress boundaries that will be employed to achieve the sought analytical solution for the sequential excavation of tunnels of elliptical cross-sections in viscoelastic rock. In the following the term “general solution” is used to indicate the mathematical solution to the set of differential equations ruling the problem without any boundary conditions imposed whereas “particular solution” indicates a solution which satisfies both the set of differential equations ruling the problem and the boundary conditions.
3.1 Solving procedure
Assuming the Einstein’s convention (i.e., repeated indices indicate summation), the constitutive equations of a general linear viscoelastic solid can be expressed in the form of convolution integrals, as shown below:
where X is the position vector and \( s_{ij}^{\text{v}} \) and \( e_{ij}^{\text{v}} \) are the tensors of the stress and strain deviators, respectively, for the viscoelastic case (here the superscript ‘v’ stands for viscoelastic), defined as:
with \( \sigma_{ij}^{{}} \) and \( \varepsilon_{ij}^{{}} \) being the tensors of stresses and strains, respectively. G(t) and K(t) in Eq. (1), represent the shear and bulk relaxation modulus, respectively. The asterisk (*) in Eq. (1) indicates the convolution integral, defined as:
The Laplace transform of Eq. (1) yields the following:
where \(\fancyscript{L}\left[ {f(t)} \right] \) is a function of the variable s defined in the Laplace transform of the time function \( f(t) \), defined as:
The Laplace transform of the linear elastic constitutive equations is as follows (here the superscript ‘e’ stands for elastic):
with \( G_{\text{e}} \) and \( K_{\text{e}} \) being the elastic shear and bulk modulus, respectively. Note that Eq. (4) can be obtained from Eq. (6) by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \). Therefore, the general solution for a viscoelastic isothermal problem, satisfying the set of differential equations governing static equilibrium, kinematic compatibility and the constitutive relationship of the rock in the time-dependent domain, can be obtained by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \) in the general solution obtained for the associated elastic problem. Then, performing a Laplace inverse transform, we obtain:
where \( u_{i}^{*} (\varvec{X},t,s) \) and \( \sigma_{ij}^{*} ({\mathbf{X}},t,s) \) are the displacements and stresses, respectively, obtained by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \) in the general solution for the associated elastic problem and \( \fancyscript{L}^{ - 1} [g(s)\;] \) indicates the inverse Laplace transform, defined as:
The general viscoelastic solution in Eq. (7) contains yet unknown functions of time, t, which have to be determined by imposition of the boundary conditions. Displacement boundary conditions may be expressed as follows:
and stress boundary conditions as:
where \( {\varvec{X}}_{0} \) is the position of a point on the boundary, n j is the unit vector normal to the boundary, \( S_{\sigma } (t) \) and \( S_{u} (t) \) are the boundary surfaces where stress and displacement conditions, respectively, are applied, and \( P_{i} \)(t) and \( u_{i}^{{}} \)(t) are two prescribed functions of time. Unlike problems with time-invariant geometrical boundaries, \( {\varvec{X}}_{0} \) and \( n_{j} \) in Eq. (9), are functions of time, hence they are not constant with respect to the Laplace transform, so they cannot be taken out of the transform operator. Therefore, the relationship between the particular solution of the viscoelastic problem and the solution of the associated elastic one is unknown. Replacing \( u_{i}^{\text{v}} \) and \( \sigma_{ij}^{\text{v}} \) with the expressions in Eq. (7), Eq. (9) can be rewritten as:
The system of Eq. (10) together with Eq. (7) define the set of equations to be satisfied by the particular solution that we seek. To find the solution, complex potential theory will be employed (see the next section).
3.2 Problem Formulation
Complex potential theory has been widely used to analyze mathematical problems associated with underground constructions, especially in the analysis of non-circular openings. For a two-dimensional (2D) elastic problem, displacements and stresses can be expressed in terms of two analytical functions of complex variable, i.e., \( \varphi_{1} \left( z \right) \) and \( \psi_{1} \left( z \right) \) with \( z = x + iy \) and \( i = \sqrt { - 1} \), which are called potential functions. So stresses and displacements can be written as (Muskhelishvili 1963):
with x, y being Cartesian coordinates in the tunnel cross-section plane (see Fig. 1a),
and the above score bar being the symbol for complex conjugate. The potentials \( \varphi_{1} \left( z \right) \) and \( \psi_{1} \left( z \right) \) in Eqs. (11–13) are time dependent, since the geometric boundaries of our problem are time dependent. Consistent with the formulation of the problem illustrated in the previous section, the Laplace transforms of the equations ruling the viscoelastic problem are performed as follows:
where the function \( \gamma (s) \) appearing in Eq. (15) is obtained by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \) in κ (see Eq. 14). Analogously, the analytical expressions for \( \varphi_{2} (z,s,t) \) and \( \psi_{2} (z,s,t) \) are obtained by replacing \( G_{\text{e}} \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( s\fancyscript{L}\left[ {K(t)} \right] \) in \( \varphi_{1} (z,t) \) and \( \psi_{1} (z,t) \), respectively. Then, by performing the inverse Laplace transform of Eqs. (15)–(17) and imposing the boundary conditions, the equations for the unknown functions will be established, as shown in the following.
In our problem only boundary conditions on the stresses are present, therefore from here onwards we consider only the stress boundary, \( S_{\sigma } (t) \). The equation imposing stress boundary conditions is as follows:
where \( P_{x}^{{}} \) and \( P_{y}^{{}} \) denote the tractions acting on the boundary along the x and y directions, respectively; \( z_{\sigma } (t) \) is a generic point on the (stress) boundary, i.e., \( z_{\sigma } (t) \in S_{\sigma } (t) \); and \( z_{\text{A}} \) is an arbitrary point on the boundary.
According to the theory of complex variable representation (Muskhelishvili 1963), in case of a simply connected domain subject to a constant body force (in our case no body force is present), the two analytical functions \( \varphi_{1} \) and \( \psi_{1} \) are material parameter independent so that \( \varphi_{1} = \varphi_{2} \) and \( \psi_{1} = \psi_{2} \). Moreover, also the analytical expressions for the stresses are independent of the material parameters (see Eqs. (16) and (17)). Hence, we can simplify Eq. (18) into:
Therefore, the boundary conditions applied on the viscoelastic medium are the same as the boundary conditions applied on the associated elastic medium. Hence, also the analytical solution for the stress field is the same for both the viscoelastic medium and the associated elastic one. Concerning displacements instead, they can be obtained by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \) in the Laplace transformed expressions obtained for the elastic case.
3.3 Calculation of stresses and displacements induced by the excavation
Let us consider a rock mass initially subject to the geostatic anisotropic stress state specified in Sect. 2 (see Fig. 1b), since a reference initial time \( t{'} = 0 \). The rock mass is subject to growing displacements over time due to its viscosity. In Fig. 1b, the inner dashed line indicates the boundary \( S_{\sigma } (t{'} ) \) of the tunnel at a time \( t^{'} \ge t^{'}_{0} \), with \( t^{'}_{0} \) being the start time of excavation. Prior to the beginning of the excavation (at time \( t{'} \le t^{'}_{{0}^{ - }} \)), the tractions \( p_{x} (z_{0}^{{}} (t{'} )) \) and \( p_{y} (z_{0}^{{}} (t{'} )) \) (with \( z_{0}^{{}} (t{'} ) \) denoting a generic point on the time-dependent boundary at time \( t{'} \)) exchanged between the two bodies along \( S_{\sigma }^{{}} (t{'} ) \) may be easily calculated imposing equilibrium. After the beginning of the excavation, at any time t > \(t^{'}_{0} \), \( p_{x} (z_{0}^{{}} (t{'} )) \) and \( p_{y} (z_{0}^{{}} (t{'} )) \) are zero along the boundary of the excavated zone hence inducing displacements in the rock. Here, the excavation-induced stress, strain and displacement increments will be calculated since the beginning of the excavation. To this end, the constitutive equations (see Eq. 1) for the deviatoric stress tensor are rewritten as follows (the derivation for the isotropic part of the stress tensor is analogous):
with \( t{'} \ge t^{'}_{0} \) whilst for \( t{'} = t^{'}_{{0}^{ - }} \):
The analytical expressions of the shear relaxation modulus G for the considered viscoelastic models (see Fig. 2) are listed in Table 1. The reference time \( t{'} \) can be chosen sufficiently large so that \( t{'} \to \infty \). In case of models with limited viscosity, e.g., generalized Kelvin and Kelvin models, here called Type A models, the first two terms in Eq. (20) turn out to be equal to the first two terms in Eq. (21) (for the demonstration of this equality see Appendix 1.2), so that:
Instead, in case of models with unlimited viscosity, e.g., Burgers and Maxwell models, here called Type B models, this is not the case so that Eq. (22) no longer holds true (see Appendix 1.3). Now, for Type A models, we define \( \Delta s_{ij}^{\text{v}} (t{'} ) \equiv s_{ij}^{\text{v}} (t{'} ) - s_{ij}^{\text{v}} (t^{'}_{{0}^{ - }} ) \) and \( \Delta e_{ij}^{\text{v}} (t{'} ) \equiv e_{ij}^{\text{v}} (t{'} ) - e_{ij}^{\text{v}} (t^{'}_{{0}^{ - }} ) \), as incremental stresses and strains, respectively, induced by the tunnel excavation. Introducing a new reference time t, with \( t = t{'} - t^{'}_{0} \), then Eq. (22) may be rewritten as follows:
Note that the relationship between \( \Delta s_{ij}^{\text{v}} \) and \( \Delta e_{ij}^{\text{v}} \) is the same as the relationship between \( s_{ij}^{\text{v}} \) and \( e_{ij}^{\text{v}} \) in Eq. (1). For the field of induced stresses, strains and displacements, also the same equations of equilibrium and compatibility must be satisfied. The corresponding boundary conditions for calculating excavation induced stresses and strains are shown in Fig. 1c, and the stresses prescribed along the boundaries (see Eq. (18)) may be written as follows:
Note that the tractions \( p_{x} \) and \( p_{y} \) applied on the inner boundary in Fig. 1b, and in Fig. 1c are of equal absolute value, but of opposite direction.
The solution procedure employed for Type B models cannot be used since Eq. (22) no longer holds true. In case of Type B models, the rock before excavation undergoes continuous displacements (see Eq. (61) in Appendix 1.1). So, to calculate the excavation-induced displacements the rock will be assumed elastic before the excavation takes place.
As outlined in Sect. 3.2, the solution for the displacements can be obtained from the solution of the associated elastic problem. The elastic solution for our problem will be obtained as the combination of two fictitious cases here called case A and B according to the principle of superposition. In case of no tractions on the inner boundary (see Fig. 1a), we obtain Solution A-ela (elastic solutions of case A); while the case of a plane without hole subject to the boundary stresses in Fig. 1b is referred to as Solution B-ela (elastic solutions of case B). Therefore, the elastic induced solutions, i.e., Solution C-ela, may be obtained by subtracting Solution B-ela from Solution A-ela. In the following section, the solutions will be derived by means of complex potential theory.
3.4 Derivation of the Analytical Solution
The method of conformal mapping provides a very powerful tool to solve problems involving complex geometries. Let us consider the complex plane z = x + iy with x and y representing the horizontal and vertical directions, respectively, in the plane of the tunnel cross-section (see Fig. 1). Also let us define a function to map the (infinite) domain (in the z plane) of the rock surrounding the elliptical cross-section into a fictitious domain (in the ζ-plane with \( \zeta = \eta + i\xi \)) with a unit circular hole. Since the elliptical cross-section varies over time, the mapping function is time dependent too:
where
If \( \frac{a(t)}{b(t)} \) is constant during the excavation stage, the excavation expands homothetically and m remains constant over time. According to the boundary conditions shown in Fig. 1a, two complex potentials for the elastic problem A with time-dependent boundaries may be derived as follows (Muskhelishvili 1963):
According to elasticity theory, the two potentials calculating the elastic displacements of an infinite plane subject to the anisotropic initial stress state prior to excavation (Solution B-ela) are as follows (Einstein and Schwartz 1979):
According to the superposition principle of elasticity, the potentials for calculating the excavation-induced displacements are as follows (Solution C-ela):
Substituting Eqs. (30) and (31) into Eqs. (11), (12) and (13), the elastic displacements and stresses (Solution C-ela) on the plane \( \zeta \) may be calculated.
According to the analysis in Sect. 3.2, the solution for the viscoelastic case can be obtained by applying the principle of correspondence, and the Laplace inverse transform of the variables (stresses, strains, etc.) calculated for the elastic case with the variable z treated as a constant in the Laplace transform. However, in Eqs. (30) and (31) the variable \( \zeta \) appears rather than z. To replace \( \zeta \) with z and t, the inverse function of the conformal mapping \( \zeta = f_{0} \left( {z,t} \right) \) needs to be found. If \( \zeta \) in Eqs. (30) and (31) is replaced with \( f_{0} \left( {z,t} \right) \), then all the time-dependent functions in Eqs. (30) and (31) may be Laplace transformed, and the viscoelastic solution may be derived from Eqs. (15), (16) and (17). Then, defining:
and substituting in Eq. (25), the following is obtained:
If the excavation process is homothetic, i.e., m is a constant, then there is no variable t in Eq. (33), and the inverse conformal mapping may be expressed as (Zhang et al. 2001):
with the yet undetermined coefficients \( A,\;A_{k} \left( {k = 0,\;1, \ldots ,\;\infty } \right) \). For numerical reasons, the series will be truncated to a finite number, l, of terms to calculate the function approximately. Due to the fact that the inverse conformal mapping is derived from the corresponding direct conformal mapping, there is a one-to-one correspondence between all the values of one function, with the values of the other function. Let us choose a number of points \( \zeta_{j} \) \( (j = 1,\;2, \ldots ,\;q) \), with q = 160, lying on the inner boundary of the unit circle in the \( \zeta \) plane to calculate the corresponding points \( z_{j}^{'} \) lying on the inner boundary in the \( z{'} \) plane using Eq. (33). Then, q linear equations for \( A \) and \( A_{k} \) can be obtained by substituting \( \zeta_{j} \) and \( z_{j}^{'} \) into Eq. (34):
Since the number of independent equations is larger than the number of unknown coefficients (\( A \), \( A_{0} \), \( A_{1} \), …, \( A_{l} \)), the system is indeterminate. To solve the system, i.e., to determine the unknown coefficients, we employed the method of minimum least squares. The non-zero coefficients obtained for the elliptical shapes here considered, are listed in Table 2 for l = 15. In Fig. 3, the curves on plane \( z{'} \) and \( \zeta \) determined by direct and inverse conformal mapping, respectively, are plotted for various shapes of the elliptical tunnel boundary. The ellipses on the \( z{'} \) plane (plotted in Fig. 3a-1, b-1, c-1), map into the circles plotted as dashed lines on the \( \zeta \) plane (Fig. 3a-2, b-2, c-2), which are determined via Eq. (25). The curves with continuous line on the \( \zeta \) plane have been obtained by inverse conformal mapping (see Eq. 34), applied to the ellipses on the \( z{'} \) plane. It can be observed that curves determined by inverse conformal mapping, are very close to circular. However, we can observe that the inverse conformal mapping is less accurate for the inner boundary when m is larger than 0.4. According to the direct and inverse conformal mappings, a one-to-one correspondence for points on the z and \( \zeta \) plane is established. For a general non-homothetic excavation process, the parameter m is a function of time, so that an analytical expression for the inverse conformal mapping cannot be obtained. However, discrete values of the inverse conformal mapping over time may be calculated according to the prescribed m(t) and c(t).
Curves determined by conformal mapping and inverse conformal mapping: a-1, b-1, c-1 ellipses in plane \( z' \) (\( z' = x' + y'i \)) determined by conformal mapping for m = 0.45, 0.4 and 0.3, respectively; a-2, b-2, c-2 mapped circles (continuous line) in plane ζ (\( \zeta = \xi + \eta i = re^{{i\theta_{1} }} \)) determined by inverse conformal mapping
Substituting Eqs. (30), (31), (34) into Eqs. (15), (16) and (17), the excavation-induced displacements and stresses in linearly viscoelastic rock (Solution C-vis) can be derived as follows:
with
Because the stresses of the viscoelastic and elastic cases are the same, the stresses of case A are the total stresses in the rock, and can be calculated by the two potentials of Solution A-ela, as:
If α is the angle between the horizontal axis x and the normal direction (see Fig. 1a), the excavation induced tangential and normal displacements and stresses around the boundary of the excavation may be calculated as follows:
The total tresses are the following:
The expressions for stresses here provided are suitable for all linear viscoelastic models, since the stress state depends only on the shape and size of the opening; conversely displacements depend on the viscoelastic model considered. The analytical solution for the displacements is provided in the next section.
3.5 Displacement solution for the generalized Kelvin model
Rock masses which have strong mechanical properties or are subject to low stresses exhibit limited viscosity. For this type of behavior, the generalized Kelvin viscoelastic model (see Fig. 2a) is commonly employed (Dai et al. 2004). On the other hand, weak, soft or highly jointed rock masses and/or rock masses subject to high stresses are prone to excavation-induced continuous viscous flows. In this case, the Maxwell model (see Fig. 2b) is suitable to simulate their rheology, due to the fact that this model is able to account for secondary creep. In this section, the analytical solution for the generalized Kelvin model is developed. The constitutive parameters of this model are as follows: (1) the elastic shear moduli G H, due to the Hookean element in the model; (2) G K, due to the spring element of the Kelvin component; (3) the viscosity coefficient η K, due to the dashpot element of the Kelvin component (see Fig. 2c). The solution for the Maxwell model may be obtained as a particular case of the generalized Kelvin model, for G K = 0. The solution for the Kelvin model (see Fig. 2c) may also be obtained as another particular case of the generalized Kelvin model for \( G_{\text{H}} \to \infty \).
Assuming that the rock is incompressible, i.e., \( K\left( t \right) \to \infty \), the two relaxation moduli appearing in the constitutive equations (see Eq. 1) are as follows:
The induced displacements, Solution C-vis, may be derived by substituting Eq. (46) into Eq. (41):
with \( B_{5} (z,t) = \int_{0}^{t} {\frac{{H(t,\tau )c\left( \tau \right)\left[ {1 - \lambda + (1 + \lambda )m(\tau )} \right]}}{{f_{1} [z'(\tau )]}}{\text{d}}\tau } \), \( B_{6} (z,t) = z\int_{0}^{t} {H(t,\tau )} \left[ {\frac{1 - \lambda + (1 + \lambda )m(\tau )}{{f_{1}^{2} [\overline{z'(\tau )} ] - m(\tau )}}} \right]{\text{d}}\tau \), \( B_{7} (z,t) = \int_{0}^{t} {\frac{{H(t,\tau )c\left( \tau \right)\left[ {\left( {1 + m^{2} (\tau )} \right)(1 + \lambda ) + 2m(\tau )(1 - \lambda )} \right]}}{{f_{1} [\overline{{z{'} (\tau )}} ]}}{\text{d}}\tau } \), \( B_{8} (z,t) = \int_{0}^{t} {\frac{{H(t,\tau )c\left( \tau \right)\left[ {\lambda - 1 - (1 + \lambda )m(\tau )} \right]\left[ {1 + m^{2} (\tau )} \right]}}{{f_{1} [\overline{{z{'} (\tau )}} ]\left\{ {f_{1}^{2} [\overline{{z{'} (\tau )}} ] - m(\tau )} \right\}}}} {\text{d}}\tau \), and
Note that when m = 0 and λ = 1, the problem reduces to a circular tunnel subject to a hydrostatic state of stress hence the problem becomes axisymmetric. The solution in Eq. (47) is degenerate and coincides with the solution provided in (Wang and Nie 2010).
4 Comparison with FEM Results
Two types of FEM analyses were run employing the FEM code ANSYS (version 11.0, employing the module of structural mechanics). The first FEM analysis wants to replicate the viscoelastic problem of solution A-vis; whereas the second one, the problem of solution C-vis. All FEM analyses were carried out with a small displacement formulation to be consistent with the derivation of the analytical solution.
The analytical solution A-vis for generalized Kelvin viscoelastic model can be derived by substituting Eqs. (27), (28), (34) and (46) into Eqs. (15)–(17). The expression for the displacements is as follows:
where \( B_{9} (z,t) = (1 - \lambda )\overline{z} \int_{0}^{t} {H(t,\tau ){\text{d}}\tau } \). Displacements and stresses of solution C-vis and stresses of solution A-vis can be found in Eqs. (47), (37), (38), (39) and (40), respectively.
First, we shall compare displacements and stresses of solution A-vis obtained by the analytical solution with the FEM analysis along three directions (horizontal, vertical, 49.8° over the horizontal). Second, the excavation-induced stresses and displacements from the analytical solution C-vis and FEM along the line (49.8° over the horizontal) will be compared to validate the analytical solution achieved. In the FEM analysis of case A-vis, initial stresses are applied on a planar domain having an elliptical hole with the major axis being 2a 0 long and minor axis 2b 0 long (part I in Fig. 4). Then, the rock is sequentially excavated at different times (see part II to VII in Fig. 4), as listed in Table 3. In the second simulation instead, initial stresses are first applied on a finite rectangular domain without hole, then an excavation starting after 50 days is simulated. Part I to VII are excavated at t′ = 50th day, 51th day, …, 56th day, respectively. Finally, the excavation-induced stresses and displacements can be obtained by subtracting the initial values before excavation from the ones calculated in the excavation stage. In the FEM analyses, elements are deleted at the time of excavation by setting the stiffness of the deleted elements to zero (by multiplying the stiffness matrix by 10−6).
A vertical stress, \( p_{0} = 10\;{\text{MPa}} \), and a horizontal stress, \( \lambda p_{0} \) with \( \lambda = 0.5 \), were applied at the boundaries of the domain. The rock was simulated as a generalized Kelvin medium, with the following constitutive parameters adopted: \( G_{\text{H}} = 2,000\;{\text{MPa}} \), \( G_{\text{K}} = 1,000\;{\text{MPa}} \) and \( \eta_{\text{K}} = 10,000\;{\text{MPa}}\;{\text{day}} \). The excavation sequence here considered is specified by the values of the major and minor axes of the elliptical section listed in Table 3 with an initial value of 2a 0 = 3.0 m for the major axis and 2b 0 = 2.0 m for the minor axis. Note that the ratio m(t) = const, i.e., the elliptical section evolves homothetically. The FEM mesh nearby the hole is plotted in Fig. 4.
The points and lines selected for comparison between the FEM analysis and the analytical solution are plotted in Fig. 5: three points on the inner boundary (Points 1, 2, 3 in Fig. 5) and three lines, one horizontal (Line 1), one vertical (Line 3) and one inclined at 49.8° over the horizontal (Line 2), were chosen. In Fig. 6, displacements and stresses for Points 1, 2 and 3 are plotted versus time. In Figs. 7 and 8 displacements and stresses, respectively, at four different times (t = 1st, 3rd, 6th and 20th days) are plotted for Lines 1, 2 and 3 versus the distance to the center of the ellipse. It emerges that the predictions from the analytical solution are in excellent agreement with the results from the FEM analysis. Obviously displacements and stresses undergo a stepwise increase following instantaneous excavation events (1st, 2nd, 3rd,… 6th days, see Fig. 6).
Comparison between analytical solution and FEM results in terms of stresses and displacements versus time for Points 1, 2, 3 (location shown in Fig. 5): a displacements at Points 1, 2 and 3; b stresses at Points 1 and 3; c stresses at Point 2
Comparison between analytical solution and FEM results in terms of displacements along Lines 1, 2 and 3 (locations shown in Fig. 5) versus distance to the ellipse center at different times (t = 1st, 3rd, 6th and 20th days): a displacements along Lines 1 and 3; b displacement along Line 2
Comparison between analytical solution and FEM results in terms of stresses along Lines 1, 2 and 3 (locations shown in Fig. 5) versus distance to the ellipse center at different times (t = 1st, 3rd, 6th and 20th days): in a–c the stresses along Lines 1, 2 and 3, respectively, are plotted
In Fig. 9, the excavation-induced displacements and stresses along Line 2 obtained from the analytical solution and FEM analysis are plotted. A good agreement in terms of both stresses and displacements can be observed. Unlike the case of solution A, almost all the induced displacements are decreasing functions of the distance to the center of the ellipse.
5 Parametric Investigation
To study the influence of excavation rate and methods, as well as the time-dependent displacements and stresses, a parametric investigation is carried out in this section. Assuming an axisymmetric elastic problem, i.e., circular tunnel in infinite plane, subject to hydrostatic initial stress p 0, with tunnel radius \( R^{*} = (a_{1} + b_{1} )/2 \) and shear modulus \( G_{\text{S}} = {{G_{\text{H}} G_{\text{K}} } \mathord{\left/ {\vphantom {{G_{\text{H}} G_{\text{K}} } {(G_{\text{H}} + G_{\text{K}} )}}} \right. \kern-0pt} {(G_{\text{H}} + G_{\text{K}} )}} \) which is the permanent modulus of the generalized Kelvin model (see Fig. 2a), the excavation-induced radial displacement at the inner boundary of the tunnel can be calculated as follows:
In the following analysis, the induced displacements will be normalized by the displacement listed in Eq. (50), and the stresses by \( - p_{0}^{{}} \). Therefore, positive dimensionless normal stresses are compression in the presented figures. Now, let us define the dimensional parameter \( T_{\text{K}} = \eta_{\text{K}} /G_{\text{K}} \), which expresses the retardation time of the Kelvin component of the generalized Kelvin model. It is convenient to normalize the time as \( t/T_{\text{K}} \) for the generalized Kelvin model. For the Maxwell model, \( G_{\text{K}} \) is equal to zero (see Fig. 2b), hence \( T_{\text{K}} \) can not be used for normalization; instead, the relaxation time \( T_{\text{M}} = \eta_{\text{K}} /G_{\text{H}} \) was employed to normalize the time as \( t/T_{\text{M}} \).
5.1 Influence of the excavation rate
To investigate the influence of the excavation rate a continuous excavation will be simulated in this section rather than a step-like one. As an example, to illustrate the difference resulting from such an approximation, the displacements and stresses obtained for step-like and continuous excavations for the generalized Kelvin model are plotted in Fig. 10. From the figure it can be seen that they are quite similar.
Concerning sequential excavation, the values of half major and minor axes grow from zero to the final values. In this case, a linear increase of the tunnel axis over time is assumed when t is less than t 1, i.e., \( a(t) = \left\{ {\begin{array}{*{20}l} {a_{0} + v_{\text{r}} t} & {0 \le t < t_{1} } \\ {a_{1} } & {t \ge t_{1} } \\ \end{array} } \right. \), where v r is the (constant) speed of cross-section excavation. It is convenient to express the half major axis in dimensionless form as:
where \( n_{\text{r}}^{\text{K}} \) is the dimensionless excavation speed, defined as follows:
In the parametric analysis \( a_{0} /a_{1} = 1/4 \) was assumed together with the following dimensionless excavation speeds: (1) \( n_{\text{r}}^{\text{K}} \to \infty \), corresponding to the case of instantaneous excavation (implying \( t_{1} /T_{\text{K}} = 0 \)); (2) \( n_{\text{r}}^{\text{K}} = 1.5 \) (implying \( t_{1} /T_{\text{K}} = 0.5 \)); (3) \( n_{\text{r}}^{\text{K}} = 0.75 \) (implying \( t_{1} /T_{\text{K}} = 1.0 \)); and (4) \( n_{\text{r}}^{\text{K}} = 0.5 \) (implying \( t_{1} /T_{\text{K}} = 1.5 \)). Concerning the excavation method, a homothetic excavation with the constant ratio \( a(t)/b(t) = 2.0 \) (\( m = 1/3 \)) is assumed in the analysis, with the ratio of horizontal over vertical stresses λ = 1/3.
To cover the wide range of responses for rock types of different viscous characteristics, the time-dependent displacements and stresses were analyzed for two types of rocks of different stiffness ratios: G K/G H = 0.5 and 2.0. In Figs. 11 and 12, the time-dependent radial and tangential displacements for the rock along the final tunnel face (i.e., along the visible face of the tunnel obtained at the end of sequential excavation) with angle \( \theta = 0^{ \circ } \), \( 45^{ \circ } \) and \( 90^{ \circ } \) are plotted for the types of rock and excavation rates considered. The symbol ‘•’ represents the end time of excavation, t 1. The figures show that the normal displacement increases with time and reaches a constant value after a certain period of time; however, the tangential displacement first decreases with time and increases rapidly towards the end of the excavation, then subsequently it reaches a constant value. Comparing Fig. 11 with Fig. 12, the final displacements are reached later for rocks with small stiffness ratios (Fig. 11). It can also be noted that the bigger the stiffness ratio, the larger the displacements occurring after excavation are. For both types of rock, the results show that a lower excavation rate implies a longer excavation time, which in turn leads to a larger value of normal displacement at the tunnel wall with \( \theta = 45^{ \circ } \) and \( 90^{ \circ } \) when \( t = t_{1} \); however, the tangential displacement at \( \theta = 45^{ \circ } \) and the normal displacement at \( \theta = 0^{ \circ } \) show no significant difference among the various excavation rates at time \( t = t_{1} \). It can also be observed that higher excavation rates imply larger normal displacements at any time, and the maximum absolute value of the tangential displacement during the excavation stage will be larger.
Generalized Kelvin model: Normalized displacement versus time normalized by \( T_{\text{K}} \) at points on the final tunnel face for various excavation rates (for G K/G H = 0.5); a normal displacement at the point with \( \theta = 0^{ \circ } \); b normal displacement at the point with \( \theta = 90^{ \circ } \); c, d normal and tangential displacements, respectively at the point with \( \theta = 45^{ \circ } \)
Generalized Kelvin model: Normalized displacement versus time normalized by \( T_{\text{K}} \) at points on the final tunnel face for various excavation rates (for G K/G H = 2.0); a normal displacement at the point with \( \theta = 0^{ \circ } \); b normal displacement at the point with \( \theta = 90^{ \circ } \); c, d normal and tangential displacements, respectively at the point with \( \theta = 45^{ \circ } \)
The Maxwell model is suitable to simulate the rheology of weak, soft or highly jointed rock, exhibiting a continuous linear viscous response when constant stresses are applied. When G K = 0, the Maxwell model is obtained (Fig. 2b). In this case, according to Eq. (50), \( G_{\text{S}}^{{}} = 0 \), and \( u_{\text{s}}^{\text{e}} \to \infty \). Hence, to normalize the displacements, a different normalization must be employed. To achieve this, we chose to replace \( G_{\text{S}} \) with \( G_{\text{H}} \) in Eq. (50) to calculate the radial displacement at the tunnel wall, i.e., \( u_{s0}^{\text{e}} = - p_{0} R^{*} /(2G_{\text{H}} ) \). In this case, we adopt \( n_{\text{r}}^{\text{M}} = \frac{{v_{\text{r}} T_{\text{M}} }}{{a_{1} }} \) as the dimensionless excavation rate with \( T_{\text{M}} = {{\eta_{\text{K}} } \mathord{\left/ {\vphantom {{\eta_{\text{K}} } {G_{\text{H}} }}} \right. \kern-0pt} {G_{\text{H}} }} \), and we consider the following four excavation rates in our analysis: (1) \( n_{\text{r}}^{\text{M}} \to \infty \); (2) \( n_{\text{r}}^{\text{M}} = 1.5 \); (3) \( n_{\text{r}}^{\text{M}} = 0.75 \); and (4) \( n_{\text{r}}^{\text{M}} = 0.5 \). In Fig. 13, the normalized displacements at the final tunnel wall at point \( \theta = 45^{ \circ } \) are plotted against the normalized time t/T M. In Fig. 13, the displacements after excavation grow linearly over time since the stresses of the rock are constant (see Eqs. (44) and (45)). Also, it emerges that the influence of the excavation rate for Maxwell model is similar to that for the generalized Kelvin model.
Observing Eqs. (44) and (45), it is shown that the stresses depend only on the size and shape of the opening, hence given a prescribed sequential excavation the stress field is identical for all the viscoelastic models. In Fig. 14, the principal stresses of the rock at the tunnel wall at points \( \theta = 0^{ \circ } \), \( \theta = 45^{ \circ } \) and \( \theta = 90^{ \circ } \), are plotted for various excavation rates. As it can be expected, the variation of stresses with time is more gradual for lower excavation rates. In all the cases, the maximum difference between the two principal stresses occurs after excavation.
Normalized principal stresses versus time normalized by \( T_{\text{K}} \) for the generalized Kelvin model and by \( T_{\text{M}} \) for the Maxwell model at different locations on the final tunnel face for various excavation rates; a–c principal stresses at points \( \theta = 0^{ \circ } \), \( \theta = 45^{ \circ } \) and \( \theta = 90^{ \circ } \), respectively
5.2 Influence of the Excavation Methods
In this section, the final values of the major and minor axes and the ratio of horizontal over vertical stresses λ are the same as in the previous section with the end time of excavation being t 1/T K = 1.0. The time-dependent tunnel inner boundaries, which simulate the real across-section excavation process as center drift advanced method (Miura et al. 2003) (e.g., method C shown in Fig. 15), and drilling and blasting method (Tonon 2010) (e.g., methods A, B1 and B2 shown in Fig. 15), are shown in Fig. 15a–c. The functions a(t) and b(t) are plotted in Fig. 16 with their analytical expressions provided in Table 4.
Sequential excavation methods A and C are stepwise excavations, in which parts ① to ⑤ (or ① to ④) are excavated instantaneously in succession. In Fig. 15, it is shown that the shape of the opening in method A first changes from ellipse to circle, and then to ellipse, by sequential excavation along the major axis direction. Obviously, the excavation is non-homothetic. Figure 16 shows that in this method the adopted excavation rate is faster at the beginning and slower near the end of excavation. In method C, the initial shape of the opening is circular, then gradually changes to elliptical with the ratio a(t)/b(t) increasing over time. The excavation rate is slower at the beginning and becomes faster near the end of excavation, which is opposite to what happens in method A. Excavation methods B1 and B2 instead, are continuous homothetic excavations (a(t)/b(t) = 2.0). Method B1 consists of a linear excavation at uniform speed, whereas method B2 consists of an excavation function a(t) in quadratic form, with a faster excavation rate at the end.
The time-dependent normal and tangential displacements at the final tunnel face are plotted in Figs. 17 and 18 for the four excavation methods considered. It emerges that the induced displacements are sensitive to the excavation method adopted. In particular it can be observed that the methods with faster speeds in the early stages lead to larger normal displacements at any time considered (except for the case of \( \theta = 0^{ \circ } \)). For all the excavation methods, the normal displacements at \( \theta = 45^{ \circ } \) and \( 90^{ \circ } \) increase over time and reach a constant positive value after a certain period of time; whereas the normal displacements at \( \theta = 0^{ \circ } \) are approximately zero in the early stages of excavation, and increase rapidly near the end of excavation for methods B1, B2 and C. The tangential displacements at \( \theta = 45^{ \circ } \) in Fig. 17d are negative and first decrease in the early stages and then increase to positive values.
Normalized excavation-induced displacements versus normalized time at some points lying on the final tunnel face for various excavation rates (for G K/G H = 0.5); a–c normal displacements at points with \( \theta = 0^{ \circ } \), \( \theta = 45^{ \circ } \) and \( \theta = 90^{ \circ } \), respectively; d tangential displacement at point with \( \theta = 45^{ \circ } \)
Normalized excavation-induced displacements versus time at points on final tunnel wall for various excavation rates (for the type of rock with G K/G H = 2.0); a–c normal displacements at point with \( \theta = 0^{ \circ } \), \( \theta = 45^{ \circ } \) and \( \theta = 90^{ \circ } \), respectively; d tangential displacement at a point with \( \theta = 45^{ \circ } \)
To analyze the difference of displacements among the excavation methods considered, the normalized displacements of methods A and C and the ratio of their differences at time t = t 1 (the difference between methods A and C is the largest one among all the methods according to Figs. 17 and 18) are listed in Table 5. The ratio of the difference of the normal displacements for a rock with G K/G H = 0.5 ranges from 26 to 33 %. The ratio for the tangential displacements is up to 60 %. For the case of G K/G H = 2.0, the ratios range from 7 to 13 % for normal displacements and up to 20 % for tangential displacements.
Figure 19 presents the normalized principal stresses calculated at the final tunnel face. It may be observed that the stresses show no difference for all of the excavation methods when \( t \ge t_{1} \), because the final shape and size of the tunnel are the same. However, during the excavation stage the stress field is clearly affected by the excavation method adopted. This stress analysis accounting for sequential excavation is valuable to check for potential failure mechanisms since it provides the stress state at any time for any point in the rock.
5.3 Distribution of Displacements and Stresses for Different Excavation Methods
In this section, the distributions of displacements and stresses assuming G K/G H = 0.5 are analyzed, adopting sequential excavation methods A and C for the same end time of excavation. Four points in time are considered in the following analysis: time t (1): t (1)/T K = 0.0, the beginning of excavation; time t (2): t (2)/T K = 0.5, during the excavation stage; time t (3): t (3)/T K = 1.0, the end of excavation; and time t (4): t (4)/T K = 2.5, the time after excavation when no further displacements practically occur.
Figure 20 presents the contour plots of the normal displacements at times t (3) and t (4) for methods A and C, respectively; and Fig. 21 presents the contour plots of the tangential displacements. Figure 20 shows that, the spatial distribution of normal displacements at the same time after excavation (e.g., the displacements in Fig. 20a and c and in Fig. 20b and d), is very similar. However, the values of displacement at the same position exhibit a significant difference especially around the tunnel crown when t = t (3). Conversely at t (4), the difference is very small. Figure 21 shows that the maximum negative tangential displacement occurs inside the ground, and the maximum positive one occurs at the tunnel face with θ approximately equal to 10°–30°. Furthermore, also the distribution of tangential displacements for different excavation methods is very similar. In Fig. 22a, b, the contours of the major and minor principal stresses, respectively, are plotted at time t (3).
Contours for tangential displacement induced by excavation method A and C at different times. a, b Contours for method A at times \( t = T_{\text{K}} \) and \( t = 2.5T_{\text{K}} \), respectively; c, d Contours for method C at times \( t = T_{\text{K}} \) and \( t = 2.5T_{\text{K}} \), respectively
Figure 23a, b present the distribution of normal and tangential displacements at the final tunnel face as a function of the angle θ for excavation method A and C at various times, which due to the symmetry of the problem, is illustrated in the range \( \theta = 0^{ \circ } \) to \( 90^{ \circ } \) only. It emerges that the normal displacement is a monotonically increasing function of the angle, and the curve shapes for various excavation methods are similar. However, at times t (2) and t (3), the values of normal displacement for the two excavation methods are significantly different. Unlike the normal displacement, the tangential displacement increases with θ for \( 0 < \theta < \theta_{\hbox{max} } \), then decreases for \( \theta_{\hbox{max} } < \theta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} \). Furthermore, the angle corresponding to the maximum displacement, \( \theta_{\hbox{max} } \), decreases over time. At time t (2) (during the excavation stage), the sign of the tangential displacement is opposite in the two excavation methods, exhibiting approximately the same \( \theta_{\hbox{max} } \). Considering the difference of induced tangential displacements between the two excavation methods, at the end of excavation it is smaller, whereas it becomes larger afterwards with a rapid decrease of displacement in method C. In addition, the angle corresponding to the maximal value, \( \theta_{\hbox{max} } \), is larger in method A than that in method C. The difference between the displacements of the two methods is smallest when t/T K = 2.5 (t (4)).
In Fig. 24a, b, the principal stresses at the final tunnel face as a function of the angle θ are plotted for methods A and C, respectively. Because the stresses depend only on the size and shape of the opening, the stresses at time t (4), which are the same as the ones at time t (3), are not included in the figure. It can be noted that at the end time of excavation, t/T K = 1.0, the distribution of stresses is the same whatever excavation method is adopted, with the largest compressive major principal stress being at \( \theta = 0^{ \circ } \). Conversely, the distribution of stresses during excavation is significantly different for the two excavation methods.
6 Conclusions
Analytical expressions of the stresses and displacements in the rock for deeply buried elliptical tunnels excavated in viscoelastic rocks were derived accounting for sequential excavation processes. An initial anisotropic stress field was assumed so that complex geological conditions can be accounted for, with the rock mass modeled as linearly viscoelastic. Solutions were derived for a sequential excavation process, with the major and minor axes of the tunnel growing monotonically, according to time-dependent functions to be specified by the designers.
First, an extension of the principle of correspondence to solve viscoelastic problems involving time-dependent stress boundaries was laid out employing the Laplace transform technique and complex potential theory. From the problem formulation, it emerges that the stress field depends only on the shape and size of the opening, whereas displacements are a function of the rock rheological properties. The methodology described in this paper may in principle be applied to obtain analytical solutions for any other arbitrary cross-sectional shapes of tunnels excavated in viscoelastic rock.
The solution for sequentially excavated tunnels of elliptical cross-section was derived by introducing an inverse conformal mapping which allows eliminating the variable t from the conformal mapping in the two complex potentials. The analytical integral expressions of the solution obtained for the generalized Kelvin viscoelastic model include the Maxwell and Kelvin models as particular cases. To validate the methodology, FEM analyses were run. A good agreement between analytical solution and FEM analyses was shown.
Finally, a parametric analysis for various excavation rates and excavation methods was performed from which the following conclusions may be drawn:
-
Slow excavation rates lead to larger normal displacements at the end of the excavation time, whilst tangential displacements show no significant difference for various excavation rates. The maximum absolute value of tangential displacement during the sequential excavation stage is larger for slower excavation rates.
-
For rocks of small stiffness ratios, G K/G H, the final steady state is reached later with the displacements occurring after the end of the excavation process being larger.
-
Sequential excavation methods prescribing a faster excavation rate in the early stages lead to larger normal displacements and smaller absolute values of negative tangential displacements but larger positive ones after excavation.
-
Normal displacements increase with the angle from the horizontal of the direction considered, whereas tangential displacements show first an increase then a decrease. The angle of the orientation corresponding to the maximum tangential displacement becomes smaller over time.
Change history
18 February 2020
The article Analytical Solutions for Tunnels of Elliptical Cross-Section in Rheological Rock Accounting for Sequential Excavation, written by H. N. Wang, S. Utili, M. J. Jiang, P. He, was originally published.
Abbreviations
- A, A 0 and A i (\( i = 1,\;2, \ldots ,\;\infty \)):
-
Coefficients in inverse conformal mapping
- \( A_{i}^{{j{\text{B}}}} \) and \( A_{ij}^{{k{\text{B}}}} \) :
-
Coefficients correlated to coordinates and material parameters of generalized Kelvin model in Appendix
- \( A_{i}^{{j{\text{M}}}} \) and \( A_{ij}^{{k{\text{M}}}} \) :
-
Coefficients correlated to coordinates and material parameters of Maxwell model in Appendix
- a(t):
-
Function of half major axis with respect to time
- a 0 :
-
Initial value of half major axis (at time t = 0)
- a 1 :
-
Final value of half major axis
- B i (\( i = 1,\;2, \ldots ,\;9 \)):
-
Coefficients in displacement solutions
- \( B_{i}^{j} \) (\( i = 1,\;2 \); \( j = 1,\;2 \)):
- b(t):
-
Function of half minor axis with respect to time
- b 0 :
-
Initial value of half minor axis (at time t = 0)
- b 1 :
-
Final value of half minor axis
- \( C_{i}^{\text{B}} \) (\( i = 1,\;2 \)):
-
Coefficients correlated to material parameters of generalized Kelvin model in Appendix
- \( C_{1}^{\text{M}} \) :
-
Coefficients correlated to material parameters of Maxwell model in Appendix
- c(t):
-
Parameter in conformal mapping (defined in Eq. (26))
- d :
-
Ratio of major over minor axis
- D i (\( i = 1,\;2 \)):
-
Coefficients in stress solutions (in Eq. 37)
- \( F_{i}^{j} \) (\( i = 1,\;2 \); \( j = 1,\;2 \)):
- f 0 :
-
Inverse conformal mapping with respect to variable z
- f 1 :
-
Inverse conformal mapping with respect to variable z 1
- G(t):
-
Time-dependent relaxation shear modulus for viscoelastic model
- G e :
-
Shear modulus of elastic problem
- G H :
-
Shear elastic modulus of the Hookean element in the Generalized Kelvin model
- G K :
-
Shear elastic modulus of the Kelvin element in the Generalized Kelvin model
- G S :
-
Permanent shear modulus of the generalized viscoelastic model: \( G_{\text{S}} = {{G_{\text{H}} G_{\text{K}} } \mathord{\left/ {\vphantom {{G_{\text{H}} G_{\text{K}} } {(G_{\text{H}} + G_{\text{K}} )}}} \right. \kern-0pt} {(G_{\text{H}} + G_{\text{K}} )}} \)
- H :
-
Function defined in Eq. (48)
- I 1 and I 2 :
-
Function defined in Eq. (59)
- K(t):
-
Time-dependent relaxation bulk modulus in the rock viscoelastic model
- K e :
-
Bulk modulus of elastic problem
- l :
-
Number of items in inverse conformal mapping
- m(t):
-
Parameter in conformal mapping (defined in Eq. (26))
- n j :
-
Vector indicating the direction normal to the boundary
- \( (n_{\chi } ,\;n_{\tau } ) \) :
-
Local coordinates
- \( n_{\text{r}}^{\text{K}} \) :
-
Normalized excavation rate for the generalized Kelvin model
- \( n_{\text{r}}^{\text{M}} \) :
-
Normalized excavation rate for the Maxwell model
- P i (\( i = 1,\;2,\;3 \)):
-
Prescribed time-dependent stresses at stress boundary
- P x (P y ):
-
Tractions (surface forces) along the x (y) direction on the stress boundary
- p 0 :
-
Vertical compressive stress at infinity
- p x (p y ):
-
Boundary tractions (surface forces) applied on the tunnel wall to calculate the excavation-induced displacements and stresses
- q :
-
Number of points adopted to determine the coefficients of inverse conformal mapping
- R * :
-
Radius of the axisymmetric problem used to normalize displacements
- \( S_{\sigma } \) (\( S_{u} \)):
-
Time-dependent stress (displacement) boundaries
- s :
-
Variable in the Laplace transform
- \( s_{ij}^{\text{e}} \), \( e_{ij}^{\text{e}} \) :
-
Tensors of the stress and strain deviators for the elastic case
- \( s_{ij}^{\text{v}} \), \( e_{ij}^{\text{v}} \) :
-
Tensors of the stress and strain deviators for the viscoelastic case
- \( T_{\text{K}} \) :
-
Retardation time of Kelvin component of the generalized Kelvin viscoelastic model
- \( T_{\text{M}} \) :
-
Relaxation time of the Maxwell viscoelastic model
- t :
-
Time variable (t = 0 is the beginning of excavation)
- \( t_{1} \) :
-
End time of excavation
- \( t{'} \) :
-
Time variable (\( t{'} \) = 0 is the time the initial pressure applied)
- \( t_{0}^{'} \) :
-
Start time of excavation
- \( u_{i}^{{}} \) :
-
Prescribed displacements on the displacement boundary
- \( u_{x}^{{({\text{A}}){\text{v}}}} \)(\( u_{y}^{{({\text{A}}){\text{v}}}} \)):
-
Displacement corresponding to viscoelastic problem of case A (in Cartesian coordinates)
- \( u_{x}^{{({\text{C}}){\text{v}}}} \)(\( u_{y}^{{({\text{C}}){\text{v}}}} \)):
-
Excavation-induced displacement for viscoelastic problem (in Cartesian coordinates)
- \( u_{\chi }^{{({\text{C}}){\text{v}}}} \)(\( u_{\tau }^{{({\text{C}}){\text{v}}}} \)):
-
Excavation-induced displacement for viscoelastic problem (in local coordinates)
- \( u_{x}^{\text{e}} \) (\( u_{y}^{\text{e}} \)):
-
Displacement along x (y) direction for the elastic problem
- \( u_{x}^{\text{s}} \) (\( u_{y}^{\text{s}} \)):
-
Prescribed displacement along x and y direction on displacement boundary
- \( u_{x}^{\text{v}} \) (\( u_{y}^{\text{v}} \)):
-
Displacement along x (y) direction for the viscoelastic problem
- \( u_{i}^{\text{v}} \) (\( \sigma_{ij}^{\text{v}} \)):
-
Displacements (stresses) tensor for the viscoelastic problem
- \( u_{s}^{\text{e}} \) :
-
Radial displacement at the tunnel wall for the axisymmetric elastic problem with radius \( R^{*} \) and shear modulus \( G_{\text{S}} \)
- \( u_{s0}^{\text{e}} \) :
-
Radial displacement at the tunnel wall for the axisymmetric elastic problem with radius \( R^{*} \) and shear modulus \( G_{\text{H}} \) in the Maxwell model
- \( u_{i}^{*} \) (\( \sigma_{ij}^{*} \)):
-
Displacements (stresses) tensor obtained by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \) in the general solution for the associated elastic problem
- v r :
-
Cross-section excavation rate
- X :
-
Position vector of a point on the plane
- X 0 :
-
Position vector of a point on the boundary
- (x, y):
-
Cartesian coordinates
- z :
-
Complex variable: z = x + iy
- z A :
-
Arbitrary point on the boundary
- z 0 :
-
Generic point on the time-dependent boundary at time \( t{'} \)
- z σ :
-
Point on time-dependent stress boundary
- z 1 :
-
Complex variable defined in Eq. (32)
- z 1j :
-
Boundary points in z 1 plane determined by Eq. (33) corresponding to point \( \zeta_{j}^{{}} \)
- α :
-
Angle between \( n_{\chi } \) and x direction
- \( \delta \) :
-
Dirac delta function
- \( \delta_{ij} \) :
-
Unit tensor
- \( \gamma \) :
-
Function with respect to s obtained by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \) in \( \kappa \)
- \( \Delta P_{x}^{{}} \)(\( \Delta P_{y}^{{}} \)):
-
Prescribed stresses along the boundaries in calculation of excavation-induced displacements and stresses
- \( \Delta s_{ij}^{\text{v}} \) (\( \Delta e_{ij}^{\text{v}} \)):
-
Incremental stresses (strains) induced by tunnel excavation
- \( \zeta \) :
-
Complex variable: \( \zeta = \xi + \eta i \)
- \( \zeta_{j}^{{}} \) :
-
Points in \( \zeta \) plane determined by Eq. (34) corresponding to point z 1
- \( \eta \) :
-
Imaginary part of \( \zeta \)
- \( \eta_{\text{K}} \) :
-
Viscosity coefficient of the dashpot element in the generalized Kelvin model
- \( \kappa \) :
-
Material coefficient defined by Eq. (14)
- \( \lambda \) :
-
Ratio of horizontal over vertical stress
- \( \xi \) :
-
Real part of \( \zeta \)
- \( (\rho ,\;\theta ) \) :
-
Polar coordinates
- \( \sigma_{ij}^{\text{v}} \) (\( \varepsilon_{ij}^{\text{v}} \)):
-
Stress (strain) tensor for viscoelastic case
- \( \sigma_{kk}^{\text{e}} \) (\( \varepsilon_{kk}^{\text{e}} \)):
-
Mean stress (strain) for elastic case
- \( \sigma_{kk}^{\text{v}} \) (\( \varepsilon_{kk}^{\text{v}} \)):
-
Mean stress (strain) for viscoelastic case
- \( \sigma_{x}^{\text{v}} \), \( \sigma_{y}^{\text{v}} \) :
-
Normal stress along x and y direction for viscoelastic case
- \( \sigma_{x}^{\text{e}} \), \( \sigma_{y}^{\text{e}} \) :
-
Normal stress along x and y direction for elastic case
- \( \sigma_{xy}^{\text{v}} \) (\( \sigma_{xy}^{\text{e}} \)):
-
Shear stress for viscoelastic (elastic) case
- \( \sigma_{x}^{{({\text{A}})}} \), \( \sigma_{y}^{{({\text{A}})}} \), \( \sigma_{xy}^{{({\text{A}})}} \) :
-
Stresses corresponding to viscoelastic problem of case A (in global Cartesian coordinates)
- \( \sigma_{x}^{{({\text{C}})}} \), \( \sigma_{y}^{{({\text{C}})}} \), \( \sigma_{xy}^{{({\text{C}})}} \) :
-
Excavation-induced stresses (in global Cartesian coordinates)
- \( \sigma_{\chi }^{{({\text{A}})}} \), \( \sigma_{\tau }^{{({\text{A}})}} \), \( \sigma_{\chi \tau }^{{({\text{A}})}} \) :
-
Stresses corresponding to viscoelastic problem of case A (in local Cartesian coordinates)
- \( \sigma_{\chi }^{{({\text{C}})}} \), \( \sigma_{\tau }^{{({\text{C}})}} \), \( \sigma_{\chi \tau }^{{({\text{C}})}} \) :
-
Excavation-induced stresses (in local Cartesian coordinates)
- \( \varphi_{1}^{{}} \) and \( \psi_{1}^{{}} \) :
-
Two complex potentials
- \( \varphi_{2}^{{}} \) and \( \psi_{2}^{{}} \) :
-
Two complex potentials obtained by replacing \( G_{\text{e}} \) with \( s\fancyscript{L}\left[ {G(t)} \right] \) and \( K_{\text{e}} \) with \( s\fancyscript{L}\left[ {K(t)} \right] \) in \( \varphi_{1}^{{}} \) and \( \psi_{1}^{{}} \)
- \( \varphi_{1}^{{({\text{A}})}} \) and \( \psi_{1}^{{({\text{A}})}} \) :
-
Two complex potentials for the elastic problem A
- \( \varphi_{1}^{{({\text{B}})}} \) and \( \psi_{1}^{{({\text{B}})}} \) :
-
Two complex potentials for the elastic problem B
- \( \varphi_{1}^{{({\text{C}})}} \) and \( \psi_{1}^{{({\text{C}})}} \) :
-
Two complex potentials for calculating the excavation-induced displacements and stresses for the elastic case
- \( \omega \) :
-
Conformal mapping determined in Eq. (25)
References
Amberg R (1983) Design and construction of the Furka base tunnel. Rock Mech Rock Eng 16:215–231
Anagnostou G, Ehrbar H (2013) Tunnelling Switzerland. Vdf Hochschulverlag AG an der ETH Zurich
Brady B, Brown E (1985) Rock mechanics for underground mining. George Allen & Unwin, London
Christensen RM (1982) Theory of viscoelasticity: an introduction, 2nd edn. Academic Press, New York
Dai HL, Wang X, Xie GX, Wang XY (2004) Theoretical model and solution for the rheological problem of anchor-grouting a soft rock tunnel. Int J Pressure Vessels Piping 81:739–748
Einstein HH, Schwartz CW (1979) Simplified analysis for tunnel supports. ASCE J Geotech Eng Div 104(4):499–518
Exadaktylos GE, Stavropoulou MC (2002) A closed-form elastic solution for stresses and displacements around tunnels. Int J Rock Mech Min Sci 39(7):905–916
Exadaktylos GE, Liolios PA, Stavropoulou MC (2003) A semi-analytical elastic stress-displacement solution for notched circular openings in rocks. Int J Solids Struct 40(5):1165–1187
Gnirk PF, Johnson RE (1964) The deformational behavior of a circular mine shaft situated in a viscoelastic medium under hydrostatic stress. In: Proceeding of 6th symposium rock mechanics. University of Missouri, Rolla, pp 231–259
Gurtin ME, Sternberg E (1962) On the linear theory of viscoelasticity. Arch Ration Mech Anal 11:291–356
Hochmuth W, Kritschke A, Weber J (1987) Subway construction in Munich, developments in tunneling with shotcrete support. Rock Mech Rock Eng 20:1–38
Jaeger JC, Cook NGW, Zimmerman RW (2007) Fundamentals of rock mechanics, 4th edn. Blackwell, USA
Ladanyi B, Gill D (1984) Tunnel lining design in creeping rocks. Symposium on design and performance of underground excavations. ISRM, Cambridge
Lee EH (1955) Stress analysis in viscoelastic bodies. Q Appl Math 13:183
Lei GH, Ng CWW, Rigby DB (2001) Stress and displacement around an elastic artificial rectangular hole. J Eng Mech ASCE 127(9):880–890
Malan DF (2002) Simulating the time-dependent behavior of excavations in hard rock. Rock Mech Rock Eng 35(4):225–254
Miura K (2003) Design and construction of mountain tunnels in Japan. Tunn Undergr Space Technol 18:115–126
Miura K, Yagi H, Shiroma H, Takekuni K (2003) Study on design and construction method for the New Tomei-Meishin expressway tunnels. Tunn Undergr Space Technol 18:271–281
Muskhelishvili NI (1963) Some basic problems of the mathematical theory of elasticity. Noordhoff, Groningen
Sharifzadeh M, Daraei R, Broojerdi M (2012) Design of sequential excavation tunneling in weak rocks through findings obtained from displacements based back analysis. Tunn Undergr Space Technol 28:10–17
Steiner W (1996) Tunneling in squeezing rocks: case histories. Rock Mech Rock Eng 29:211–246
Sulem J, Panet M, Guenot A (1987a) Closure analysis in deep tunnels. Int J Rock Mech Min Sci Geomech Abstr 24(3):145–154
Sulem J, Panet M, Guenot A (1987b) An analytical solution for time-dependent displacements in circular tunnel. Int J Rock Mech Min Sci Geomech Abst 24(3):155–164
Tonon F (2010) Sequential excavation, NATM and ADECO: What they have in common and how they differ. Tunn Undergr Space Technol 25:245–265
Wang HN, Nie GH (2010) Analytical expressions for stress and displacement fields in viscoelastic axisymmetric plane problem involving time-dependent boundary regions. Acta Mech 210:315–330
Wang HN, Nie GH (2011) Solutions for viscoelastic axisymmetric plane problem involving time-dependent boundary regions under mixed boundary condition. Acta Mech 216:59–73
Wang HN, Li Y, Ni Q, Utili S, Jiang MJ, Liu F (2013) Analytical solutions for the construction of deeply buried circular tunnels with two liners in rheological rock. Rock Mech Rock Eng 46(6):1481–1498
Wang HN, Utili S, Jiang MJ (2014) An analytical approach for the sequential excavation of axisymmetric lined tunnels in viscoelastic rock. Int J Rock Mech Min Sci 68:85–106
Wone M, Nasri V, Ryzhevskiy M (2003) Rock tunnelling challenges in Manhattan. In: 29th ITA World Tunnelling Congress, Amsterdam, vol 1, pp 145–151
Zhang LQ, Lu AZ, Yang ZF (2001) An analytic algorithm of stresses for any double hole problem in plane elastostatics. J Appl Mech ASME 68(2):350–353
Acknowledgments
This work is supported by National Basic Research Program of China (973 Program) with Grant No.2014CB046901; State Key Lab. Of Disaster Reduction in Civil Engineering (Grant No. SLDRCE14-B-11); Marie Curie Actions—International Research Staff Exchange Scheme (IRSES): GEO—geohazards and geomechanics with Grant No. 294976; China National Funds for Distinguished Young Scientists with Grant No. 51025932. These supports are greatly appreciated.
Author information
Authors and Affiliations
Corresponding author
Appendix 1
Appendix 1
This appendix presents the analytical derivation of the first two terms in Eqs. (20) and (21) for the purpose of calculating the excavation-induced stresses and displacements. The two Eqs. (20) and (21) are listed in the following as Eqs. (53) and (54):
The first and second terms in Eq. (53) are as follows:
The corresponding terms in Eq. (54) are as follows:
The expressions for displacements and strain rates in the rock before the excavation starts needed in the derivation, are obtained in Appendix 1.1. Note that the exact expressions of the coefficients are not given, since only the form of functions of the coefficients with respect to the given parameters are necessary in the demonstration.
1.1 1.1 Expressions for Displacements and Strain Rates Before the Excavation
Substituting Eq. (29) into Eq. (15), and assuming that:
The displacements occurred prior to the excavation can be calculated as (solution B-vis):
Substituting the functions expressing the shear and bulk relaxation moduli for the adopted viscoelastic model into Eq. (60), the explicit expressions can be obtained. If only shear viscoelasticity is considered, i.e., K(t) = K e, displacements can be derived as follows:
where the terms with subscript i = 1 denote the components along the x direction, and i = 2 denote the components along the y direction. The coefficients \( A_{i}^{{j{\text{M}}}} \), \( A_{i}^{{j{\text{B}}}} \) (i = 1, 2 and j = 1–3) are determined via Eq. (60).
According to Eqs. (61) and (62), and the strain–displacement relationships, \( \varepsilon_{ij}^{\text{v}} = \frac{1}{2}[u_{i,j}^{\text{v}} + u_{j,i}^{\text{v}} ] \), as well as the definition of strain deviators given in Eq. (2), the derivative of strain deviators for time t’ can be calculated as follows:
For models with unlimited viscosity (Type B models), e.g., Burgers model, the expressions for displacement and strain rate are analogous to Eqs. (61) and (63), where the values of the coefficients A to be used depend on the rheological models; conversely for models of limited viscosity, e.g., Kelvin model, the expressions are analogous to Eqs. (62) and (64).
1.2 1.2 Derivation for the generalized Kelvin model
According to the expression of G(t) for the generalized Kelvin model in Eq. (46), when time tends to infinity or is large enough, G(t) will be a constant, which is a general law for Type A viscoelastic models. Because the excavation started at a time much later than the time when the initial stresses were applied, the time \( t_{0}^{'} \) (beginning of excavation,), and the generic time \( t{'} \ge t^{'}_{0} \), can be assumed to be infinite. Therefore, \( G(t{'} ) = G(t_{0}^{'} ) \) and the first terms in Eqs. (53) and (54) are equal, that is \( F_{1}^{1} = F_{1}^{2} \).
Substituting Eq. (46) into Eq. (56), yields
where \( C_{1}^{B} \) and \( C_{2}^{B} \) are coefficients independent of time, and:
Substituting Eq. (46) into Eq. (58), yields:
where:
It can be noted from Eqs. (66) and (68) that \( B_{2}^{1} = B_{2}^{2} \). Substituting Eq. (64) into the expression of \( B_{1}^{1} \) (in Eq. 66), yields:
After integration, then rearranging:
where \( \lambda_{3} = \lambda_{B} - \lambda_{B1} > 0 \), \( \lambda_{4} = \lambda_{B} - \lambda_{B2} > 0 \). When \( t{'} \to \infty \) and \( t_{0}^{'} \to \infty \), Eq. (70) becomes:
Substituting Eq. (64) into the expression of \( B_{1}^{2} \) yields:
when \( t_{0}^{'} \to \infty \), \( B_{1}^{2} = 0 \). According to Eqs. (65) and (67), as well as the fact that \( B_{2}^{1} = B_{2}^{2} \), \( B_{1}^{1} = B_{1}^{2} = 0 \), the second term of Eq. (53) is equal to that of Eq. (54), that is, \( F_{2}^{1} = F_{2}^{2} \). Owing to the fact that the first and second term in Eq. (53) are equal to the corresponding terms in Eq. (54), the equality between the sums of the first and second terms in Eqs. (53) and (54) is demonstrated. This equality is used in Sect. 3.3. An analogous demonstration can be carried out for rheological models with limited viscosity (Type A).
1.3 1.3 Derivation for the Maxwell model
The expression of G(t) for the Maxwell model is in the form of an exponential function as shown in Table 1. It is obvious that \( G(t{'} ) = G(t_{0}^{'} ) \) because \( t{'} \)(\( t{'} > t_{0} \)) and \( t_{0}^{'} \) can be regarded as infinite. Substituting \( G(t{'} ) = G(t_{0}^{'} ) \) into Eqs. (55) and (57) yields \( F_{1}^{1} = F_{1}^{2} \). Therefore, the first terms from Eqs. (53) and (54) are equal. For any value of \( t{'} \) and \( t_{0}^{'} \), the second term of Eq. (53) can be written as:
The term \( \exp \left( { - \lambda_{{{\text{M}}2}} (t{'} - t_{0}^{'} )} \right) \) is non zero. The second term of Eq. (54) can be written as:
After integration and rearranging, yields:
When \( t{'} \to \infty \) and \( t_{0}^{'} \to \infty \), the above equation becomes:
According to Eqs. (73) and (76), the second terms in Eqs. (53) and (54) are not equal, but hold the relationship shown in Eq. (73).
Rights and permissions
This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, H.N., Utili, S., Jiang, M.J. et al. Analytical Solutions for Tunnels of Elliptical Cross-Section in Rheological Rock Accounting for Sequential Excavation. Rock Mech Rock Eng 48, 1997–2029 (2015). https://doi.org/10.1007/s00603-014-0685-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-014-0685-7