Skip to main content

Advertisement

SpringerLink
Log in

A review on vibrating beam-based micro/nano-gyroscopes

  • Review Paper
  • Published:
Microsystem Technologies Aims and scope Submit manuscript

Abstract

A comprehensive review of the modeling approaches used to simulate the behaviors of micro/nano-gyroscopes is presented. The performance and sensitivity of these inertial sensors can be significantly improved through understanding their governing dynamics and exploiting specific phenomena and distinctive features. Such understanding can be developed by solving and analyzing their governing equations and boundary conditions that may comprise a set of highly nonlinear partial differential equations. The operating principle of vibrating beam gyroscopes is described and their main actuation and sensing mechanisms are reviewed and discussed. The multi-fidelity modeling approaches that have been used for the design, performance analysis, and control of vibratory micro/nano-gyroscopes are consolidated and reviewed. The use of these mathematical models has opened doors for the development of new sensing designs with unprecedented sensitivity and extended operating range. To date, extensive research has been conducted on modeling and simulations of micro/nano-gyroscopes. However, several open research topics have not been thoroughly explored yet. These include nanoscale experimentation for model validation, damage/fatigue modeling, and self-powered energy harvesting gyroscope systems. This review presents the current state of the art and highlights promising research directions for continued technological advancement of micro/nano-gyroscopes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

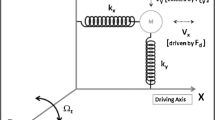
Adapted from (Kambali and Pandey 2015)

Fig. 8
Fig. 9

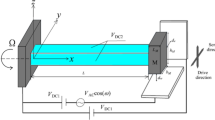
(adopted from Younis 2011)

Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  • Acar C, Shkel A (2008) MEMS vibratory gyroscopes: structural approaches to improve robustness. Springer Science & Business Media

  • Acar C, Schofield AR, Trusov AA, Costlow LE, Shkel AM (2009) Environmentally robust MEMS vibratory gyroscopes for automotive applications. IEEE Sens J 9(12):1895–1906

    Article  Google Scholar 

  • Adams SG, Groves J, Shaw KA, Davis TJ, Cardarelli D, Carroll R, Fontanella MD (1999) Single-crystal silicon gyroscope with decoupled drive and sense. Micromachined Devices Components V 3876:74–83

    Article  Google Scholar 

  • Alcheikh N, Hajjaj AZ, Jaber N, Younis MI (2018) Electrothermally actuated tunable clamped-guided resonant microbeams. Mech Syst Signal Proc 98:1069–1076

    Article  Google Scholar 

  • Alper SE, Azgin K, Akin T (2007) A high-performance silicon-on-insulator MEMS gyroscope operating at atmospheric pressure. Sens Actuators, A 135(1):34–42

    Article  Google Scholar 

  • Bai Y, Tofel P, Palosaari J, Jantunen H, Juuti J (2017) A game changer: a multifunctional perovskite exhibiting giant ferroelectricity and narrow bandgap with potential application in a truly monolithic multienergy harvester or sensor. Adv Mater 29(29)

  • Bazaei A, Moheimani S (2014) A comprehensive analysis of MEMS electrothermal displacement sensors. IEEE Sens J 14(9):3183–3192

    Article  Google Scholar 

  • Bestetti M, Zega V, Langfelder G (2020) Modeling and first characterization of broad-spectrum vibration rejection of frequency modulated gyroscopes. 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS), pp. 259–262

  • Bevan J (1998) Analysis and testing of plates with piezoelectric sensors and actuators

  • Bhadbhade V, Jalili N, Mahmoodi SN (2008) A novel piezoelectrically actuated flexural/torsional vibrating beam gyroscope. J Sound Vib 311(3–5):1305–1324

    Article  Google Scholar 

  • Cao Y, Sepúlveda N (2019) Design of flexible piezoelectric gyroscope for structural health monitoring. Appl Phys Lett 115(24)

  • Cao L, Fan S, Guo Z, Xu L (2016) A method to simulate the vibrating characters of the resonator for resonant MEMS gyroscope. Microsyst Technol 22(9):2315–2327

    Article  Google Scholar 

  • Cao H, Liu Y, Kou Z, Zhang Y, Shao X, Gao J, Huang K, Shi Y, Tang J, Shen C, Liu J (2019) Design, fabrication and experiment of double U-beam MEMS vibration ring gyroscope. Micromachines 10(3):186

    Article  Google Scholar 

  • Cao H, Xue R, Cai Q, Gao J, Zhao R, Shi Y, Shen C (2020a) Design and experiment for dual-mass MEMS gyroscope sensing closed-loop system. IEEE Access 8:48074–48087

    Article  Google Scholar 

  • Cao LM, Li JW, Liu XW, Sun FY (2020b) Research on an anchor point lever beam coupling type tuning fork micro-gyroscope. Int J Precision Eng Manufacturing: 1–13

  • Chang H, Zhang Y, Xie J, Zhou Z, Yuan W (2010) Integrated behavior simulation and verification for a MEMS vibratory gyroscope using parametric model order reduction. J Microelectromech Syst 19(2):282–293

    Article  Google Scholar 

  • Chew Z, Ruan T, Zhu M, Bafleur M, Dilhac J (2016) A multifunctional device as both strain sensor and energy harvester for structural health monitoring. IEEE SENSORS 1–3

  • Cho J, Kim K, Hwang W, Yang C, Ahn J, Hong S, Jeon D, Song G, Ryu C, Woo S, Kim J, Lee T, Choi J, Cheong H, Sung T (2019) A multifunctional road-compatible piezoelectric energy harvester for autonomous driver assited LED indicators with a self monotoring system. Appl Energy 242:294–301

    Article  Google Scholar 

  • Choa SH (2005) Reliability of vacuum packaged MEMS gyroscopes. Microelectron Reliab 45(2):361–369

    Article  Google Scholar 

  • Cook R, DelRio F, Boyce B (2019) Predicting strength distributions of MEMS structures using flaw size and spatial density. Microsyst Nanoeng 5(1):1–12

    Article  Google Scholar 

  • Deng Q, Kammoun M, Erturk A, Sharma P (2014) Nanoscale flexoelectric energy harvesting. Int J Solids Struct 51(18):3218–3225

    Article  Google Scholar 

  • Edamana B, Chen Y, Slavin D, Aktakka EE, Oldham KR (2015) Estimation with threshold sensing for gyroscope calibration using a piezoelectric microstage. IEEE Trans Control Syst Technol 23(5):1943–1951

    Article  Google Scholar 

  • Efimovskaya A, Wang D, Lin Y, Shkel A (2018) Electrostatic compensation of structural imperfections in dynamically amplified dual-mass gyroscope. Sens Actuators, A 275:99–108

    Article  Google Scholar 

  • Efimovskaya A, Wang D, Shkel A (2020) Mechanical trimming with focused ion beam for permanent tuning of MEMS dual-mass gyroscope. Sens Actuators, A 313:112189

    Article  Google Scholar 

  • Erturk A, Inman DJ (2008) On mechanical modeling of cantilevered piezoelectric vibration energy harvesters. J Intell Mater Syst Struct 19(11):1311–1325

    Article  Google Scholar 

  • Esmaeili M, Durali M, Jalili N (2006) Ring microgyroscope modeling and performance evaluation. J Vib Control 12(5):537–553

    Article  MATH  Google Scholar 

  • Esmaeili M, Jalili N, Durali M (2007) Dynamic modeling and performance evaluation of a vibrating beam microgyroscope under general support motion. J Sound Vib 301(1–2):146–164

    Article  Google Scholar 

  • Gao S, Huang H (2017) Recent advances in micro-and nano-machining technologies. Front Mech Eng 12(1):18–32

    Article  MathSciNet  Google Scholar 

  • Geiger W, Folkmer B, Merz J, Sandmaier H, Lang W (1999) A new silicon rate gyroscope. Sens Actuators, A 73(1–2):45–51

    Article  Google Scholar 

  • Gentili E, Tabaglio L, Aggogeri F (2005) Review on micromachining techniques. In AMST’05 advanced manufacturing systems and technology, Vienna, Springer, pp. 387–396

  • Ghayesh MH, Farokhi H, Alici G (2016) Size-dependent performance of microgyroscopes. Int J Eng Sci 100:99–111

    Article  MathSciNet  MATH  Google Scholar 

  • Ghommem M, Abdelkefi A (2017a) Nonlinear analysis of rotating nanocrystalline silicon microbeams for microgyroscope applications. Microsyst Technol 23(12):5931–5946

    Article  Google Scholar 

  • Ghommem M, Abdelkefi A (2017b) Performance analysis of differential-frequency microgyroscopes made of nanocrystalline material. Int J Mech Sci 133:495–503

    Article  Google Scholar 

  • Ghommem M, Abdelkefi A (2017c) Novel design of microgyroscopes employing electrostatic actuation and resistance-change based sensing. J Sound Vib 411:278–288

    Article  Google Scholar 

  • Ghommem M, Abdelkefi A (2017d) Modeling and Design Enhancement of Differential-Frequency Microgyroscopes Made of Nanocrystalline Material. In ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers Digital Collection

  • Ghommem M, Nayfeh AH, Choura S, Najar F, Abdel-Rahman EM (2010) Modeling and performance study of a beam microgyroscope. J Sound Vib 329(23):4970–4979

    Article  Google Scholar 

  • Ghommem M, Nayfeh AH, Choura S (2013) Model reduction and analysis of a vibrating beam microgyroscope. J Vib Control 19(8):1240–1249

    Article  MathSciNet  Google Scholar 

  • Giannini D, Braghin F, Aage N (2020) Topology optimization of 2D in-plane single mass MEMS gyroscopes. Structural and Multidisciplinary Optimization, pp. 1–21

  • Giner J, Maeda D, Ono K, Shkel A, Sekiguchi T (2018) MEMS gyroscope with concentrated springs suspensions demonstrating single digit frequency split and temperature robustness. J Microelectromech Syst 28(1):25–35

    Article  Google Scholar 

  • Gladwell G (1966) A variational formulation of damped acousto structural vibration problems. J Sound Vib 4(2):172–186

    Article  MathSciNet  MATH  Google Scholar 

  • Gupta R, Rana L, Tomar M, Gupta V (2018) Characterization of lead zirconium titanate thin films based multifunctional energy harvesters. Thin Solid Films 652:39–42

    Article  Google Scholar 

  • Gurtin ME, Murdoch AI (1975) A continuum theory of elastic material surfaces. Arch Ration Mech Anal 57(4):291–323

    Article  MathSciNet  MATH  Google Scholar 

  • Hadjesfandiari AR, Dargush GF (2011) Couple stress theory for solids. Int J Solids Struct 48(10):2496–2510

    Article  Google Scholar 

  • Hajjaj AZ, Ramini A, Alcheikh N, Younis MI (2017) Electrothermally tunable arch resonator. J Microelectromech Syst 26(4):837–845

    Article  Google Scholar 

  • Hong YS, Lee JH, Kim SH (2000) A laterally driven symmetric micro-resonator for gyroscopic applications. J Micromech Microeng 10(3):452

    Article  Google Scholar 

  • Hong Y, Kim S, Lee JH (2003) Modeling of angular-rate bandwidth for a vibrating microgyroscope. Microsyst Tech 9(6–7):441–448

    Article  Google Scholar 

  • Jain A, Gopal R (2017) Structural design of torsional micro-gyroscope having robust drive and sense modes. Microsyst Technol 23(8):3429–3441

    Article  Google Scholar 

  • Kagawa Y, Tsuchiya T, Kawashima T (1996) Finite element simulation of piezoelectric vibrator gyroscopes. IEEE Trans Ultrason Ferroelectr Freq Control 43(4):509–518

    Article  Google Scholar 

  • Kagawa Y, Tsuchiya T, Sakai T (2001) Three-dimensional finite-element simulation of a piezoelectric vibrator under gyration. IEEE Trans Ultrason Ferroelectr Freq Control 48(1):180–188

    Article  Google Scholar 

  • Kagawa Y, Wakatsuki N, Tsuchiya T, Terada Y (2006) A tubular piezoelectric vibrator gyroscope. IEEE Sens J 6(2):325–330

    Article  Google Scholar 

  • Kambali PN, Pandey AK (2015) Capacitance and force computation due to direct and fringing effects in MEMS/NEMS arrays. IEEE Sens J 16(2):375–382

    Article  Google Scholar 

  • Karan S, Maiti S, Agrawal A, Das A, Maitra A, Paria S, Bera A, Bera R, Halder L, Mishra A, Kim J, Khatua B (2019) Designing high energy conversion efficient bio-inspired vitamin assisted single-structured based self-powered piezolectric/wind/accoustic multi-energy harvestyer with remarkable energy density. Nano Energy 59:169–183

    Article  Google Scholar 

  • Kawai H, Atsuchi KI, Tamura M, Ohwada K (2001) High-resolution microgyroscope using vibratory motion adjustment technology. Sens Actuators A: Phys 90(1–2):153–159

    Article  Google Scholar 

  • Keivani M, Mokhtari J, Kanani A, Abadian N, Rach R, Abadyan M (2017) A size-dependent model for instability analysis of paddle-type and double-sided NEMS measurement sensors in the presence of centrifugal force. Mech Adv Mater Struct 24(10):809–819

    Article  Google Scholar 

  • Khandelwal G, Chandrasekhar A, Pandey R, Raj N, Kim S (2019) Phase inversion enabled energy scavenger: a multifunctional triboelectric nanogenerator as benzene monitoring system. Sens Actuat B-Chem 282:590–598

    Article  Google Scholar 

  • Khodaei MJ, Mehrvarz A, Candelino N, Jalili N (2019) Theoretical and experimental analysis of coupled flexural-torsional vibrations of rotating beams. In ASME 2018 Dynamic Systems and Control Conference. American Society of Mechanical Engineers Digital Collection

  • Kim K, Song G, Park C, Yun K (2017) Multifunctional Woven structure operating as triboelectric energy harvester, capacitive tactile sensor array, and piezoresistive strain sensor array. Sensors (Basel, Switzerland) 17

  • Kuehnel W (1995) Modelling of the mechanical behavior of a differential capacitor acceleration sensor. Sens Actu A 48:101–108

    Article  Google Scholar 

  • Kugi A, Thull D, Seidel H (2004) December. Modelling and optimization of a silicon tuning fork gyroscope. In PAMM: Proceedings in Applied Mathematics and Mechanics, Berlin

  • Kumari K, Khanna G (2016) Design and simulation of array of rectangular micro cantilevers piezoelectric energy harvester. Int J Eng Res Appl 6:41–49

    Google Scholar 

  • Kwon H, Seok S, Lim G (2017) System modeling of a MEMS vibratory gyroscope and integration to circuit simulation. Sensors 17(11):2663

    Article  Google Scholar 

  • Lajimi SAM, Heppler GR, Abdel-Rahman M (2015) Primary resonance of a beam-rigid body microgyroscope. Int J Non-Linear Mech 77:364–375

    Article  Google Scholar 

  • Lajimi SAM, Heppler GR, Abdel-Rahman EM (2017a) A parametric study of the nonlinear dynamics and sensitivity of a beam-rigid body microgyroscope. Commun Nonlinear Sci Numer Simul 50:180–192

    Article  MathSciNet  MATH  Google Scholar 

  • Lajimi SAM, Heppler GR, Abdel-Rahman E (2017b) On modeling beam-rigid-body microgyroscopes. Appl Math Model 42:753–760

    Article  MathSciNet  MATH  Google Scholar 

  • Lajimi SAM, Heppler GR, Abdel-Rahman EM (2017c) A mechanical–thermal noise analysis of a nonlinear microgyroscope. Mech Syst Signal Proc 83:163–175

    Article  Google Scholar 

  • Larkin K, Ghommem M, Abdelkefi A (2018) Significance of size dependent and material structure coupling on the characteristics and performance of nanocrystalline micro/nano gyroscopes. Phys E: Low-Dimensional Syst Nanostruct 99:169–181

    Article  Google Scholar 

  • Larkin K, Ghommem M, Hunter A, Abdelkefi A (2020a) Nonlinear size dependent analysis and effectiveness of nanocrystalline micro/nanogyroscopes. Physica E 117:113808

    Article  Google Scholar 

  • Larkin K, Ghommem M, Hunter A, Abdelkefi A (2020b) Nonlinear modeling and performance analysis of cracked beam microgyroscopes. Int J Mech Sci:105965

  • Lavrik N, Datskos P (2019) Optically read Coriolis vibratory gyroscope based on a silicon tuning fork. Microsyst Nanoeng 5(1):1–11

    Article  Google Scholar 

  • Li Y, Fan S, Guo Z, Li J, Cao L (2012) Frequency measurement study of resonant vibratory gyroscopes. J Sound Vib 331(20):4417–4424

    Article  Google Scholar 

  • Li Z, Gao S, Jin L, Liu H, Guan Y, Peng S (2019a) Design and mechanical sensitivity analysis of a MEMS tuning fork gyroscope with an anchored leverage mechanism. Sensors 19(16):3455

    Article  Google Scholar 

  • Li Z, Li T, Yang Z, Naguib H (2019b) Toward a 0.33 W piezoelectric and electromagnetic hybrid energy harvester: design, experimental studies and self-powered applications. Appl Energy 255:113805

    Article  Google Scholar 

  • Li L, Lin R, Ng TY (2020) Contribution of nonlocality to surface elasticity. Int J Eng Sci 152

  • Liang X, Hu S, Shen S (2017) Nanoscale mechanical energy harvesting using piezoelectricity and flexoelectricity. Smart Mater Struct 26(3):035050

    Article  Google Scholar 

  • Liao F, Park S, Larson JM, Zachariah MR, Girshick SL (2003) High-rate chemical vapor deposition of nanocrystalline silicon carbide films by radio frequency thermal plasma. Mater Lett 57(13–14):1982–1986

    Article  Google Scholar 

  • Liu Y, Ge H, Fan Z, Chen X, Huang F, Wang Y, Hou Z, Bai G (2019a) Failure analysis and experimental validation of mems gyro under random vibration condition. In Prognostics and System Health Management Conference (PHM-Qingdao)

  • Liu H, Wei Z, Tan G, Han Y, Liu Z (2019b) Vibratory characteristics of cracked non-uniform beams with different boundary conditions. J Mech Sci Technol 33(1):377–392

    Article  Google Scholar 

  • Liu Y, Zhang S, Hou Z, Fan Z, Wang Y, Peng X, Chen X (2020) An investigate on degradation models of resonant frequency and mechanical sensitivity for butterfly resonator gyroscope. J Microelectromech Syst 29(4):468–479

    Article  Google Scholar 

  • Maenaka K, Kohara H, Nishimura M, Fujita T, Takayama Y (2006) Novel solid micro-gyroscope. In 19th IEEE International Conference on Micro Electro Mechanical Systems, pp. 634–637

  • Marschner U, Graham F, Mudivarthi C, Yoo JH, Neubert H, Flatau AB (2010) Finite element model-simulation-based characterization of a magnetostrictive gyrosensor. J Appl Phys 107(9):09E705

    Article  Google Scholar 

  • Menéndez RJP (2019) IFOG and IORG Gyros: a study of comparative performance. In Gyroscopes-Principles and Applications. IntechOpen

  • Menon PK, Nayak J, Pratap R (2018) Sensitivity analysis of an in-plane MEMS vibratory gyroscope. Microsyst Technol 24(5):2199–2213

    Article  Google Scholar 

  • Mian M, Dennis J, Khir M, Riaz K, Iqbal A, Bazaz S, Tang T (2015) MEMS 3-DoF gyroscope design, modeling and simulation through equivalent circuit lumped parameter model. In AIP Conference Proceedings

  • Mindlin RD, Tiersten HF (1962) Effects of couple-stresses in linear elasticity. Columbia University, New York

    Book  Google Scholar 

  • Mohanty A, Parida S, Behera RK, Roy T (2019) Vibration energy harvesting: a review. J Adv Dielectr 9(4):1930001

    Article  Google Scholar 

  • Mohite S, Patil N, Pratap R (2006) Design, modelling and simulation of vibratory micromachined gyroscopes. In J Phys: Conf Series

  • Mojahedi M, Ahmadian MT, Firoozbakhsh K (2013a) Dynamic pull-in instability and vibration analysis of a nonlinear microcantilever gyroscope under step voltage considering squeeze film damping. Int J Appl Mech 5(3):1350032

    Article  Google Scholar 

  • Mojahedi M, Ahmadian MT, Firoozbakhsh K (2013b) Oscillatory behavior of an electrostatically actuated microcantilever gyroscope. Int J Struct Stab Dyn 13(6):1350030

    Article  MathSciNet  MATH  Google Scholar 

  • Mojahedi M, Ahmadian M, Firoozbakhsh K (2013c) Static deflection and pull-in instability analysis of an electrostatically actuated mirocantilever gyroscope considering geometric nonlinearities. J Mech Sci Technol 27(8):2425–2434

    Article  Google Scholar 

  • Mojahedi M, Ahmadian MT, Firoozbakhsh K (2013d) The oscillatory behavior, static and dynamic analyses of a micro/nano gyroscope considering geometric nonlinearities and intermolecular forces. Acta Mech Sin 29(6):851–863

    Article  MathSciNet  MATH  Google Scholar 

  • Mojahedi M, Ahmadian MT, Firoozbakhsh K (2014a) The influence of the intermolecular surface forces on the static deflection and pull-in instability of the micro/nano cantilever gyroscopes. Compos B Eng 56:336–343

    Article  MATH  Google Scholar 

  • Mojahedi M, Ahmadian MT, Firoozbakhsh K (2014b) Effects of Casimir and Van der waals forces on the pull-in instability of the nonlinear micro and nano-bridge gyroscopes. Int J Struct Stab Dyn 14(2):1350059

    Article  MathSciNet  MATH  Google Scholar 

  • Mokhtari MA, Askari AR, Tahani M (2017) Effect of the casimir force on size-dependent dynamic pull-in instability in micro-bridge gyroscopes with a proof mass. In 7th International Conference on Acoustics and Vibration (ISAV2017)

  • Nayfeh AH, Abdel-Rahman EM, Ghommem M (2015) A novel differential frequency micro-gyroscope. J Vib Control 21(5):872–882

    Article  MathSciNet  Google Scholar 

  • Osterberg PM, Senturia SD (1997) M-TEST: a test chip for MEMS material property measurement using electrostatically actuated test structures. J Microelectromech Syst 6(2):107–118

    Article  Google Scholar 

  • Ouakad HM (2019) Nonlinear structural behavior of a size-dependent MEMS gyroscope assuming a non-trivial shaped proof mass. Microsyst Tech: 1–10

  • Ozer Z, Mamedov AM, Ozbay E (2013) Modeling and simulation of the ferroelectric based micro gyroscope: FEM analysis. Ferroelectrics 446(1):46–58

    Article  Google Scholar 

  • Painter C, Shkel A (2003) Active structural error suppression in MEMS vibratory rate integrating gyroscopes. IEEE Sens J 3(5):595–606

    Article  Google Scholar 

  • Prikhodko IP, Zotov SA, Trusov AA, Shkel AM (2012) Sub-degree-per-hour silicon MEMS rate sensor with 1 million Q-factor. 16th International Solid-State Sensors, Actuators and Microsystems Conference, pp. 2809–2812

  • Prikhodko IP, Trusov AA, Shkel AM (2013) Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing. Sens Actuators, A 201:517–524

    Article  Google Scholar 

  • Rajendran S, Liew KM (2004) Design and simulation of an angular-rate vibrating microgyroscope. Sens Actuators, A 116(2):241–256

    Article  Google Scholar 

  • Rasekh M, Khadem SE (2013) Design and performance analysis of a nanogyroscope based on electrostatic actuation and capacitive sensing. J Sound Vib 332(23):6155–6168

    Article  Google Scholar 

  • Riaz K, Bazaz SA, Saleem MM, Shakoor RI (2011) Design, damping estimation and experimental characterization of decoupled 3-DoF robust MEMS gyroscope. Sens Actuators, A 172(2):523–532

    Article  Google Scholar 

  • Saqib M, Mubasher Saleem M, Mazhar N, Awan S, Shahbaz Khan U (2018) Design and analysis of a high-gain and robust multi-DOF electro-thermally actuated MEMS gyroscope. Micromachines 9(11):577

    Article  Google Scholar 

  • Satz A, Hammerschmidt D (2007) Dynamical charaterization of a vibrating member gyroscope using finite element method

  • Saukoski M, Aaltonen L, Halonen K (2008) Effects of synchronous demodulation in vibratory MEMS gyroscopes: a theoretical study. IEEE Sens J 8:1722–1733

    Article  Google Scholar 

  • Senturia SD (2007) Microsystem design, Springer Science & Business Media

  • Shaat M, Abdelkefi A (2015) Modeling the material structure and couple stress effects of nanocrystalline silicon beams for pull-in and bio-mass sensing applications. Int J Mech Sci 101:280–291

    Article  Google Scholar 

  • Shaat M, Khorshidi MA, Abdelkefi A, Shariati M (2016) Modeling and vibration characteristics of cracked nano-beams made of nanocrystalline materials. Int J Mech Sci 115:574–585

    Article  Google Scholar 

  • Shakoor RI, Bazaz SA, Lai Y, Hasan MM (2008) Comparative study on finite element analysis & system model extraction for non-resonant 3-DoF microgyroscope. In IEEE International Behavioral Modeling and Simulation Workshop

  • Shakoor RI, Bazaz SA, Kraft M, Lai Y, Hassan U, Masood M (2009) Thermal actuation based 3-DoF non-resonant microgyroscope using MetalMUMPs. Sensors 9(4):2389–2414

    Article  Google Scholar 

  • Shakoor R, Bazaz S, Burnie M, Lai Y, Hasan M (2011a) Electrothermally actuated resonant rate gyroscope fabricated using the MetalMUMPs. Microelectron J 42(4):585–593

    Article  Google Scholar 

  • Shakoor R, Bazaz S, Saleem M (2011b) Mechanically amplified 3-dof nonresonant microelectromechanical systems gyroscope fabricated in low cost metalmumps process. J Mech Design 133(11)

  • Shakoor R, Burnie M, Iqbal S (2018) Experimental evaluation of resonant frequencies with associated mode shapes and power analysis of thermally actuated vibratory microgyroscope. Microsyst Technol 24(9):3601–3613

    Article  Google Scholar 

  • Sharma A, Zaman MF, Zucher M, Ayazi F (2008) A 0.1/HR bias drift electronically matched tuning fork microgyroscope. 21st International Conference on Micro Electro Mechanical Systems (pp. 6–9). IEEE, pp. 5–7

  • Skogström L, Li J, Mattila TT, Vuorinen V (2020) MEMS reliability. In Handbook of Silicon Based MEMS Materials and Technologies, Elsevier, pp. 851–876

  • Smith G, Pulskamp J, Sanchez L, Potrepka D, Proie R, Ivanov T, Rudy R, Nothwang W, Bedair S, Meyer C, Polcawich R (2012) PZT-based piezoelectric MEMS technology. J Am Ceram Soc 95(11):1777–1792

    Article  Google Scholar 

  • Tatar E, Alper SE, Akin T (2012) Quadrature-error compensation and corresponding effects on the performance of fully decoupled MEMS gyroscopes. J Microelectromech Syst 21(3):656–667

    Article  Google Scholar 

  • Tatar E, Mukherjee T, Fedder GK (2014) Simulation of stress effects on mode-matched MEMS gyroscope bias and scale factor. In 2014 IEEE/ION Position, Location and Navigation Symposium-PLANS 2014, pp. 16–20

  • Toupin R (1962) Elastic materials with couple-stresses

  • Trusov AA, Schofield AR, Shkel AM (2011) Micromachined rate gyroscope architecture with ultra-high quality factor and improved mode ordering. Sensors Actuators A: Phys 165(1):26–34

    Article  Google Scholar 

  • Van Der Meijs NP, Fokkema JT (1984) VLSI circuit reconstruction from mask topology. Integration 2(2):85–119

    Article  Google Scholar 

  • Verma P, Gopal R, Arya S (2013) Analytical modeling and simulation of a 2-DOF drive and 1-DOF sense gyro-accelerometer. Microsyst Technol 19:1238–1249

    Article  Google Scholar 

  • Verma P, Arya SK, Gopal R (2015) Lumped parameter analytic modeling and behavioral simulation of a 3-DOF MEMS gyro-accelerometer. Acta Mech Sin 31(6):910–919

    Article  MathSciNet  MATH  Google Scholar 

  • Wu X, Chen W, Lu Y, Xiao Q, Ma G, Zhang W, Cui F (2009) Vibration analysis of a piezoelectric micromachined modal gyroscope (PMMG). J Micromech Microeng 19(12):125008

    Article  Google Scholar 

  • Xu Q, Hou Z, Kuang Y, Miao T, Ou F, Zhuo M, Xiao D, Wu X (2019) A tuning fork gyroscope with a polygon-shaped vibration beam. Micromachines 10(12):813

    Article  Google Scholar 

  • Yang FACM, Chong ACM, Lam DCC, Tong P (2002) Couple stress based strain gradient theory for elasticity. Int J Solids Struct 39(10):2731–2743

    Article  MATH  Google Scholar 

  • Yeh BY, Liang YC, Tay FE (2001) Mathematical modelling on the quadrature error of low-rate microgyroscope for aerospace applications. Analog Integr Circuits Signal Proc 29(1–2):85–94

    Article  Google Scholar 

  • Yi-Hsuan T, Peng CC (2020) An ARMA based digital twin for MEMS gyroscope drift dynamics modeling and real-time compensation. IEEE Sensors J

  • Yoon S, Park U, Rhim J, Yang SS (2015) Tactical grade MEMS vibrating ring gyroscope with high shock reliability. Microelectr Eng (142): 22–29

  • Younis MI (2011) MEMS linear and nonlinear statics and dynamics. Springer Science & Business Media, vol. 20

  • Yu X, Long X (2015) Parametric design of mechanical dither with bimorph piezoelectric actuator for ring laser gyroscope. Int J Appl Electromagnet Mech 47(2):305–312

    Article  Google Scholar 

  • Yuan W (2017) Development and application of high-end aerospace MEMS. Front Mech Eng 12(4):567–573

    Article  Google Scholar 

  • Zhang R, Chen Z, Zhang R (2012) A micro-machined silicon vibrating ring gyroscope. In Advanced Materials Research, 403: 4244–4251

  • Zhao G, Wu Z (2017) Coupling vibration analysis of rotating three-dimensional cantilever beam. Comput Struct 179:64–74

    Article  Google Scholar 

  • Zhou B, Gao ZY, Chen H, Zhang R, Chen ZY (2006) Digital readout system for micromachined gyroscope and analysis for its demodulation algorithm. Front Mech Eng China 1(1):106–110

    Article  Google Scholar 

Download references

Acknowledgements

K. Larkin acknowledges the financial support from the Advanced Simulation and Computing (ASC)—Integrated Codes (IC) Program, through the Lagrangian Applications Project at Los Alamos National Laboratory.

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, New Mexico State University, Las Cruces, NM, 88003, USA

    K. Larkin, M. Serrano & A. Abdelkefi

  2. Los Alamos National Laboratory, Los Alamos, NM, 87545, USA

    K. Larkin

  3. Department of Mechanical Engineering, American University of Sharjah, 26666, Sharjah, United Arab Emirates

    M. Ghommem

Authors
  1. K. Larkin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Ghommem
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Serrano
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. Abdelkefi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Abdelkefi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Larkin, K., Ghommem, M., Serrano, M. et al. A review on vibrating beam-based micro/nano-gyroscopes. Microsyst Technol 27, 4157–4181 (2021). https://doi.org/10.1007/s00542-020-05191-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00542-020-05191-z

Search

Navigation