Skip to main content
SpringerLink
Log in

Chaos analysis and stability control of the MEMS resonator via the type-2 sequential FNN

  • Technical Paper
  • Published:
Microsystem Technologies Aims and scope Submit manuscript

Abstract

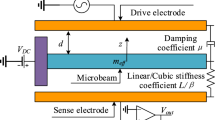
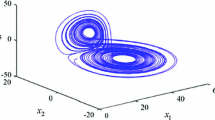
In this paper, a fuzzy stability control algorithm based on the type-2 sequential fuzzy neural network (T2SFNN) is proposed to suppress the chaotic motion of the MEMS resonator. The dynamical behaviors of the MEMS resonator are revealed by the bifurcation diagram, exponent diagram, phase diagram and corresponding time history. In the process of the controller design for backstepping control, the T2SFNN is used to tackle the unknown external disturbance and eliminate the effect of time delay, along with the cosine function to ensure that the output constraint is not violated. In addition, an absorber is employed to avoid the repeated derivative associated with the backstepping. Finally, the effectiveness of the proposed scheme is verified by numerical simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  • Arora R, Agarwal D, Bera TK (2019) Workspace analysis and trajectory tracking of a planar hybrid manipulator with ball screw feed drive. J Braz Soc Mech Sci Eng 41(9):378

    Article  Google Scholar 

  • Fossi DOT, Woafo P (2013) Generation of complex phenomena in a simple electromechanical system using the feedback control. Commun Nonlinear Sci Numer Simul 18(1):209–218

    Article  MathSciNet  Google Scholar 

  • Hajjam A, Pourkamali S (2011) Fabrication and characterization of MEMS-based resonant organic gas sensors. IEEE Sens J 12(6):1958–1964

    Article  Google Scholar 

  • He S, Sun K, Mei X, Yan B, Xu S (2017) Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative. Eur Phys J Plus 132(1):36

    Article  Google Scholar 

  • Liu YJ, Gao Y, Tong S et al (2016) Fuzzy approximation-based adaptive backstepping optimal control for a class of nonlinear discrete-time systems with dead-zone. IEEE Trans Fuzzy Syst 24(1):16–28

    Article  Google Scholar 

  • Liu H, Pan Y, Li S et al (2017) Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans Syst Man Cybern 47(8):2209–2217

    Article  Google Scholar 

  • Luo S, Song Y (2016) Chaos analysis-based adaptive backstepping control of the microelectromechanical resonators with constrained output and uncertain time delay. IEEE Trans Ind Electron 63(10):6217–6225

    Article  Google Scholar 

  • Luo S, Wang J, Wu S et al (2014) Chaos RBF dynamics surface control of brushless DC motor with time delay based on tangent barrier Lyapunov function. Nonlinear Dyn 78(2):1193–1204

    Article  Google Scholar 

  • Luo S, Lewis FL, Song Y, Vamvoudakis KG (2020a) Adaptive backstepping optimal control of a fractional-order chaotic magnetic-field electromechanical transducer. Nonlinear Dyn. https://doi.org/10.1007/s11071-020-05518-5

    Article  Google Scholar 

  • Luo S, Lewis Frank L, Song Y, Hassen M (2020b) Accelerated adaptive fuzzy optimal control of three coupled fractional-order chaotic electromechanical transduces. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/tfuzz.2020.2984998

    Article  Google Scholar 

  • Miandoab EM, Yousefi-Koma A, Pishkenari HN et al (2015) Study of nonlinear dynamics and chaos in MEMS/NEMS resonators. Commun Nonlinear Sci Numer Simul 22(1–3):611–622

    Article  Google Scholar 

  • Mohammadzadeh A, Ghaemi S (2018) Robust synchronization of uncertain fraction-order chaotic systems with time-varying delay. Nonlinear Dyn 93:1809–1821

    Article  Google Scholar 

  • Niu B, Zhao J (2013) Barrier Lyapunov functions for the output tracking control of constrained nonlinear switched systems. Syst Control Lett 62(10):963–971

    Article  MathSciNet  Google Scholar 

  • Park K, Chen Q, Lai YC (2008) Energy enhancement and chaos control in microelectromechanical systems. Phys Rev E 77(2):026210

    Article  Google Scholar 

  • Seleim A, Towfighian S, Delande E et al (2012) Dynamics of a close-loop controlled MEMS resonator. Nonlinear Dyn 69(1–2):615–633

    Article  Google Scholar 

  • Sharma M, Sarraf EH, Baskaran R et al (2012) Parametric resonance: amplification and damping in MEMS gyroscopes. Sens Actuators, A 177:79–86

    Article  Google Scholar 

  • Su Z, Li Y, Yang G, et al (2020) Dietary composition perception algorithm using social robot audition for Mandarin Chinese. In: IEEE Access, pp 8768–8782

  • Sun J, Liu C (2018) Distributed fuzzy adaptive backstepping optimal control for nonlinear multimissile guidance systems with input saturation. IEEE Trans Fuzzy Syst 27(3):447–461

    Google Scholar 

  • Tajaddodianfar F, Pishkenari HN, Yazdi MRH et al (2015) On the dynamics of bistable micro/nano resonators: analytical solution and nonlinear behavior. Commun Nonlinear Sci Numer Simul 20(3):1078–1089

    Article  MathSciNet  Google Scholar 

  • Tajaddodianfar F, Yazdi MRH, Pishkenari HN (2017) Nonlinear dynamics of MEMS/NEMS resonators: analytical solution by the homotopy analysis method. Microsyst Technol 23(6):1913–1926

    Article  Google Scholar 

  • Tee KP, Ge SS, Tay EH (2009) Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 45(4):918–927

    Article  MathSciNet  Google Scholar 

  • Timurdogan E, Alaca BE, Kavakli IH et al (2011) MEMS biosensorfor detection of Hepatitis A and C viruses in serum. Biosens Bioelectron 28(1):189–194

    Article  Google Scholar 

  • Yau HT, Wang CC, Hsieh CT et al (2011) Nonlinear analysis and control of the uncertain micro-electro-mechanical system by using a fuzzy sliding mode control design. Comput Math Appl 61(8):1912–1916

    Article  MathSciNet  Google Scholar 

  • Yin SH, Epureanu BI (2007) Experimental enhanced nonlinear dynamics and identification of attractor morphing modes for damage detection. J Vib Acoust 129(6):763–770

    Article  Google Scholar 

  • Younis MI, Nayfeh AH (2003) A Study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dyn 31(1):91–117

    Article  Google Scholar 

  • Younis MI, Ouakad HM, Alsaleem FM et al (2010) Nonlinear dynamics of MEMS arches under harmonic electrostatic actuation. J Microelectromech Syst 19(3):647–656

    Article  Google Scholar 

  • Zhankui S, Sun K (2013) Nonlinear and chaos control of a micro-electro-mechanical system by using second-order fast terminal sliding mode control. Commun Nonlinear Sci Numer Simul 18(9):2540–2548

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

This work is funded by the Science and Technology Planning Project of Guizhou Province (Nos. [2020]1Y274 and [2018]5781), National Natural Science Foundation of China (No. 61863005) and Science and Technology Foundation of Guizhou Province (Nos. [2018]5702, [2020]6007, QKHZC [2019] 2814 and [2020]4Y056).

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Guizhou University, Guiyang, 550025, China

    Le Zhao, Shaohua Luo, Guanci Yang & Rongzhi Dong

  2. Key Laboratory of Advanced Manufacturing Technology, Guizhou University, Guiyang, 550025, China

    Guanci Yang

Authors
  1. Le Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shaohua Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guanci Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Rongzhi Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shaohua Luo.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, L., Luo, S., Yang, G. et al. Chaos analysis and stability control of the MEMS resonator via the type-2 sequential FNN. Microsyst Technol 27, 173–182 (2021). https://doi.org/10.1007/s00542-020-04935-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00542-020-04935-1

Search

Navigation