Skip to main content
SpringerLink
Log in

Optimal tracking control of switched systems applied in grid-connected hybrid generation using reinforcement learning

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

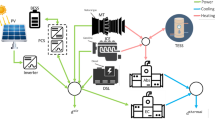
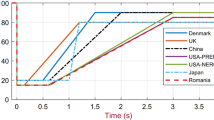
The paper presents a reinforcement learning approach for optimal tracking control of switched systems with application to a grid-tied hybrid generation system. To enhance interaction with the irregular environment, reference trajectory is learned via controller from states to optimal control. The main issue is to solve the optimal tracking control problem for a hybrid generation system consisting of multiple switched subsystems, and reinforcement learning can seek the globally optimal solution well without knowing accurate system dynamics. The investigated learning algorithm is used to generate an optimum map based on the learned ultimate value without knowledge of system parameters and obtains the optimal control law via deriving of algebraic Riccati equation (ARE) with unnecessary knowing of command generator dynamics. The optimal control solution can converge the online learning algorithm well based on policy iteration as verification in the simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Kim S, Jeon J, Cho C, Ahn J, Kwon S (2008) Dynamic modeling and control of a grid-connected hybrid generation system with versatile power transfer. IEEE Trans Ind Electron 55(4):1677–1688

    Article  Google Scholar 

  2. Jun Zhao, Dimirovski GM (2004) Quadratic stability of a class of switched nonlinear systems. IEEE Trans Autom Control 49(4):574–578

    Article  MathSciNet  Google Scholar 

  3. Aleksandrov AY, Chen Y, Platonov AV, Zhang L (2011) Stability analysis for a class of switched nonlinear systems. Automatica 47(10):2286–2291

    Article  MathSciNet  Google Scholar 

  4. Valenciaga F, Puleston PF (2005) Supervisor control for a stand-alone hybrid generation system using wind and photovoltaic energy. IEEE Trans Energy Convers 20(2):398–405

    Article  Google Scholar 

  5. Heydari A, Balakrishnan SN (2014) Optimal switching and control of nonlinear switching systems using approximate dynamic programming. IEEE Trans Neural Netw Learn Syst 25(6):1106–1117

    Article  Google Scholar 

  6. Zhang H, Qin C, Luo Y (2014) Neural-network-based constrained optimal control scheme for discrete-time switched nonlinear system using dual heuristic programming. IEEE Trans Autom Sci Eng 11(3):839–849

    Article  Google Scholar 

  7. Lewis FL, Vrabie D, Vamvoudakis KG (2012) Reinforcement learning and feedback control: using natural decision methods to design optimal adaptive controllers. IEEE Control Syst Mag 32(6):76–105

    Article  MathSciNet  Google Scholar 

  8. Yang X, He H, Zhong X (2019) Approximate dynamic programming for nonlinear-constrained optimizations. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2019.2926248

    Article  Google Scholar 

  9. Wei C, Zhang Z, Qiao W, Qu L (2015) Reinforcement-learning-based intelligent maximum power point tracking control for wind energy conversion systems. IEEE Trans Ind Electron 62(10):6360–6370

    Article  Google Scholar 

  10. Mannava A, Balakrishnan SN, Tang L, Landers RG (2012) Optimal tracking control of motion systems. IEEE Trans Control Syst Technol 20(6):1548–1558

    Article  Google Scholar 

  11. Zhang H, Cui L, Zhang X, Luo Y (2011) Data-driven robust approximate optimal tracking control for unknown general nonlinear systems using adaptive dynamic programming method. IEEE Trans Neural Netw 22(12):2226–2236

    Article  Google Scholar 

  12. Luo B, Yang Y, Liu D, Wu H (2020) Event-triggered optimal control with performance guarantees using adaptive dynamic programming. IEEE Trans Neural Netw Learn Syst 31(1):76–88

    Article  MathSciNet  Google Scholar 

  13. Wang F, Zhang H, Liu D (2009) Adaptive dynamic programming: an introduction. IEEE Comput Intell Mag 4(2):39–47

    Article  Google Scholar 

  14. Jiang Y, Jiang ZP (2012) Computational adaptive optimal control for continuous-time linear systems with completely unknown dynamics. Automatica 48(10):2699–2704

    Article  MathSciNet  Google Scholar 

  15. Lewis FL, Vamvoudakis KG (2011) Reinforcement learning for partially observable dynamic processes: adaptive dynamic programming using measured output data. IEEE Trans Syst Man Cybern Part B (Cybernetics) 41(1):14–25

    Article  Google Scholar 

  16. Tong S, Zhang L, Li Y (2016) Observed-based adaptive fuzzy decentralized tracking control for switched uncertain nonlinear large-scale systems with dead zones. IEEE Trans Syst Man Cybern Syst 46(1):37–47

    Article  Google Scholar 

  17. Hajiahmadi M, De Schutter B, Hellendoorn H (2016) Design of stabilizing switching laws for mixed switched affine systems. IEEE Trans Autom Control 61(6):1676–1681

    Article  MathSciNet  Google Scholar 

  18. Lu W, Zhu P, Ferrari S (2016) A hybrid-adaptive dynamic programming approach for the model-free control of nonlinear switched systems. IEEE Trans Autom Control 61(10):3203–3208

    Article  MathSciNet  Google Scholar 

  19. Niu B, Ahn CK, Li H, Liu M (2018) Adaptive control for stochastic switched nonlower triangular nonlinear systems and its application to a one-link manipulator. IEEE Trans Syst Man Cybern Syst 48(10):1701–1714

    Article  Google Scholar 

  20. Ni Z, He H, Wen J (2013) Adaptive learning in tracking control based on the dual critic network design. IEEE Trans Neural Netw Learn Syst 24(6):913–928

    Article  Google Scholar 

  21. Shen H, Huo S, Cao J, Huang T (2019) Generalized state estimation for Markovian coupled networks under round-robin protocol and redundant channels. IEEE Trans Cybern 49(4):1292–1301

    Article  Google Scholar 

  22. Liang H, Liu G, Zhang H, Huang T (2020) Neural-network-based event-triggered adaptive control of nonaffine nonlinear multiagent systems with dynamic uncertainties. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2020.3003950

    Article  Google Scholar 

  23. Liang H, Liu G, Huang T, Lam HK, Wang B (2020) Cooperative fault-tolerant control for networks of stochastic nonlinear systems with non-differential saturation nonlinearity. IEEE Trans Syst Man Cybern Syst. https://doi.org/10.1109/TSMC.2020.3020188

    Article  Google Scholar 

  24. Vamvoudakis KG, Lewis FL (2010) Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 46(5):878–888

    Article  MathSciNet  Google Scholar 

  25. Vrabie D, Pastravanu O et al (2009) Adaptive optimal control for continuous-time linear systems based on policy iteration. Automatica 45(2):477–484

    Article  MathSciNet  Google Scholar 

  26. Tran DH, Hamker F, Nassour J (2020) A humanoid robot learns to recover perturbation during swinging motion. IEEE Trans Syst Man Cybern Syst 50(10):3701–3712

    Article  Google Scholar 

  27. Liu M, Wan Y, Li S, Lewis FL, Fu S (2020) Learning and uncertainty-exploited directional antenna control for robust long-distance and broad-band aerial communication. IEEE Trans Veh Technol 69(1):593–606

    Article  Google Scholar 

  28. Corona D, Buisson J, De Schutter B, Giua A (2007) Stabilization of switched affine systems: an application to the buck-boost converter. In: 2007 American control conference, New York, NY, pp 6037–6042

  29. Lee JY, Park JB, Choi YH (2012) Integral Q-learning and explorized policy iteration for adaptive optimal control of continuous-time linear systems. Automatica 48(11):2850–2859

    Article  MathSciNet  Google Scholar 

  30. Zhang J, Feng T, Zhang H, Wang X (2020) The decoupling cooperative control with dominant poles assignment. IEEE Trans Syst Man Cybern Syst. https://doi.org/10.1109/TSMC.2020.3011142

    Article  Google Scholar 

  31. Jia Q, Sun M, Tang WKS (2019) Consensus of multiagent systems with delayed node dynamics and time-varying coupling. IEEE Trans Syst Man Cybern Syst. https://doi.org/10.1109/TSMC.2019.2921594

    Article  Google Scholar 

  32. Zhang J, Chen X, Gu G (2020) State consensus for discrete-time multi-agent systems over time-varying graphs. IEEE Trans Autom Control. https://doi.org/10.1109/TAC.2020.2979750

    Article  Google Scholar 

  33. Jia Q, Mwanandiye ES, Tang WKS (2020) Master–Slave synchronization of delayed neural networks with time-varying control. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2020.2996224

    Article  Google Scholar 

  34. Sun J, Zhang H, Wang Y, Sun S (2020) Fault-tolerant control for stochastic switched it2 fuzzy uncertain time-delayed nonlinear systems. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2020.2997348

    Article  Google Scholar 

  35. Sun XM, Liu GP, Rees D, Wang W (2008) Delay-dependent stability for discrete systems with large delay sequence based on switching techniques. Automatica 44(11):2902–2908

    Article  MathSciNet  Google Scholar 

  36. Xu X, Antsaklis PJ (2002) Optimal control of switched systems via nonlinear optimization based on direct differentiations of value functions. Int J Control 75(16):1406–1426

    Article  Google Scholar 

  37. Xu X, Antsaklis PJ (2004) Optimal control of switched systems based on parameterization of the switching instants. IEEE Trans Autom Control 49(1):2–16

    Article  MathSciNet  Google Scholar 

  38. Seatzu C, Corona D, Giua A, Bemporad A (2006) Optimal control of continuous-time switched affine systems. IEEE Trans Autom Control 51(5):726–741

    Article  MathSciNet  Google Scholar 

  39. Egerstedt M, Wardi Y, Axelsson H (2006) Transition-time optimization for switched-mode dynamical systems. IEEE Trans Autom Control 51(1):110–115

    Article  MathSciNet  Google Scholar 

  40. Vrabie D, Pastravanu O, Abu-Khalaf M, Lewis FL (2009) Adaptive optimal control for continuous-time linear systems based on policy iteration. Automatica 45(2):477–484

    Article  MathSciNet  Google Scholar 

  41. Lee JY, Park JB et al (2012) Integral Q-learning and explorized policy iteration for adaptive optimal control of continuous-time linear systems. Automatica 48(11):2850–2859

    Article  MathSciNet  Google Scholar 

  42. Lewis FL, Vrabie D, Syrmos V (2012) Optimal control, 3rd edn. Wiley, New York

    Book  Google Scholar 

  43. Kleinman D (1968) On an iterative technique for Riccati equation computations. IEEE Trans Autom Control 13(1):114–115

    Article  Google Scholar 

  44. Liu D, Li H, Wang D (2014) Online synchronous approximate optimal learning algorithm for multi-player non-zero-sum games with unknown dynamics. IEEE Trans Syst Man Cybern Syst 44(8):1015–1027

    Article  Google Scholar 

  45. Wang L, Lam H (2020) Further study on observer design for continuous-time Takagi–Sugeno fuzzy model with unknown premise variables via average dwell time. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2019.2933696

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by National Key R&D Program of China (2018YFA0702200), National Natural Science Foundation of China (61627809), and Liaoning Revitalization Talents Program (XLYC1801005).

Author information

Authors and Affiliations

  1. College of Information Science and Engineering, Northeastern University, Box 134, Shenyang, 110819, People’s Republic of China

    Jiayue Sun, Yingchun Wang & Mingrui Fu

  2. State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, Liaoning, 110004, China

    Huaguang Zhang

Authors
  1. Jiayue Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Huaguang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yingchun Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mingrui Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huaguang Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest. All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards. This article does not contain any studies with animals performed by any of the authors. Informed consent was obtained from all individual.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, J., Zhang, H., Wang, Y. et al. Optimal tracking control of switched systems applied in grid-connected hybrid generation using reinforcement learning. Neural Comput & Applic 33, 9363–9374 (2021). https://doi.org/10.1007/s00521-021-05696-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-021-05696-2

Keywords

Search

Navigation