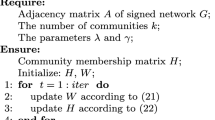Abstract
Community detection in networks including singed edges is a primary challenge that has already attracted substantial attention. In this paper, we show that this task could be reformulated as a combinatorial optimization concerning the trace of the signed modularity matrix. Keeping the orthogonal and nonnegative constraints in the relaxation, we propose a multiplicative update rule, named the SMON algorithm, which results in a solution that is a close approximation to the genuine community indication matrix. In addition, the rows of the solution can be referred to as the probabilities of corresponding vertex falling into each community, which can help us to discover the overlapping community structure of the network and identify vertices that reside on the watersheds between different communities. Experimental results on real-life social networks as well as synthetic signed networks verify that our method is effective and superior to the existing approaches.







Similar content being viewed by others
Notes
How to choose an optimal value of c will be discussed in Sect. 4.3, and we take it as a given here.
References
Palla G, Barabási A-L, Vicsek T (2007) Quantifying social group evolution. Nature 446(7136):664–667
Traud AL, Kelsic ED, Mucha PJ, Porter MA (2011) Comparing community structure to characteristics in online collegiate social networks. SIAM Rev 53(3):526–543
Flake GW, Lawrence SR, Giles CL, Coetzee FM (2002) Self-organization and identification of web communities. IEEE Comp 35(3):66–70
Guimerà R, Nunes Amaral LA (2005) Functional cartography of complex metabolic networks. Nature 433(7028):895–900
Palla G, Derényi I, Farkas I, Vicsek T (2005) Uncovering the overlapping community structure of complex networks in nature and society. Nature 435:814–818
Huss M, Holme P (2007) Currency and commodity metabolites: their identification and relation to the modularity of metabolic networks. IET Syst Biol 1(5):280–285
Newman MEJ (2003) The structure and function of complex networks. SIAM Rev 45(2):167–256
Porter MA, Onnela J-P, Mucha PJ (2009) Communities in networks. Not Am Math Soc 56(9):4294–4303
Fortunato S (2009) Community detection in graphs. Phys Rep 486(3):75–174
Girvan M, Newman MEJ (2002) Community structure in social and biological networks. Proc Natl Acad Sci USA 99(12):7821–7826
Newman MEJ (2006) Finding community structure in networks using the eigenvectors of matrices. Phys Rev E 74:036104
Newman MEJ, Leicht EA (2007) Mixture models and exploratory analysis in networks. Proc Natl Acad Sci USA 104:9564–9569
Holme P, Liljeros F, Edling CR, Kim BJ (2003) Network bipartivity. Phys Rev E 68:056107
Newman MEJ, Girvan M (2004) Finding and evaluating community structure in networks. Phys Rev E 69:026113
Guha R, Kumar R, Raghavan P, Tomkins A (2004) Propagation of trust and distrust. In: Proceedings of 13th international conference on World Wide Web, pp 403–412
Kunegis J, Lommatzsch A, Bauckhage C (2009) The slashdot zoo: mining a social network with negative edges. In: Proceedings of 18th international conference on World Wide Web, pp 741–750
Traag VA, Bruggeman J (2009) Community detection in networks with positive and negative links. Phys Rev E 80:036115
Mason MJ, Fan G, Plath K, Zhou Q, Horvath S (2009) Signed weighted gene co-expression network analysis of transcriptional regulation in murine embryonic stem cells. BMC Genom 10:327
Heider F (1946) Attitude and cognitive organization. J Psychol 21:107–112
Cartwright D, Harary F (1956) Structural balance: a generalisation of Heider’s theory. Psychol Rev 63:277–293
Davis JA (1967) Clustering and structural balance in graphs. Human Relat 20:181–187
Kaplan TD, Forrest S (2008) arXiv preprint arXiv:0801.3290
Jiang JQ (2015) Stochastic block model and exploratory analysis in signed networks. Phys Rev E 91(6):062805
Szell M, Lambiotte R, Thurner S (2010) Multirelational organization of large-scale social networks in an online world. Proc Nat Acad Sci USA 107:13636–13641
Leskovec J, Huttenlocher D, Kleinberg J (2010) Engaging with Massive Online Courses. In: Proceedings of 19th international conference on World Wide Web, pp 641–650
Huang ZX, Qiu YH (2010) A multiple-perspective approach to constructing and aggregating citation semantic link network. Future Gen Comput Syst 26(3):400–407
Gómez S, Jensen P, Arenas A (2009) Analysis of community structure in networks of correlated data. Phys Rev E 80:016114
Anchuri P, Magdon-Ismail M (2012) Communities and balance in signed networks: A spectral approach. In: Proceedings of international conference on advances in social networks analysis and mining, pp 235–242
Kernighan BW, Lin S (1970) An efficient heuristic procedure for partitioning graphs. Bell Syst Tech J 49:291–307
Yang B, Cheung WK, Liu JM (2007) Community mining from signed social networks. IEEE Trans knowl Data Eng 19(10):1333–1348
Amelio A, Pizzuti C (2013) Community mining in signed networks: A multiobjective approach. In: Proceedings of the 2013 IEEE/ACM international conference on advances in social networks analysis and mining, pp 95–99
Luo D, Ding CHQ, Huang H, Li T (2009) Non-negative Laplacian Embedding. In: Proceedings of 9th IEEE international conference on data mining, pp 337–346
Nie F, Ding C, Luo D, Huang H (2010) Multi-subspace representation and discovery. In: Proceedings of European conference on machine learning and principles and practice of knowledge discovery in databases, pp 451–466
Jiang JQ, McQuay LJ (2012) Modularity functions maximization with nonnegative relaxation facilitates community detection in networks. Physica A 391(3):854–865
Gfeller D, Chappelier JC, De Los Rios P (2005) Finding instabilities in the community structure of complex networks. Phys Rev E 72(5):056135
Nepusz T, Petróczi A, Negyessy L, Bazsó F (2008) Fuzzy communities and the concept of bridgeness in complex networks. Phys Rev E 77:016107
Psorakis I, Roberts S, Ebden M, Sheldon B (2011) Overlapping community detection using Bayesian non-negative matrix factorization. Phys Rev E 83:066114
ropivnik S, Mrvar A (1996) An analysis of the slovene parliamentary parties network. In: Ferligoj A, Kramberger A (eds) Developments in statistics and methodology, pp 209–216
Read KE (1954) Cultures of the Central Highlands, New Guinea. Southwest J Anthropol 10:1–43
Huang C, Hu B, Yang R, Wu G (2018) SNMFP: A two-stage approach to community detection in signed networks. Phys A: Stat Mech Appl 510:754–764
Jiang F, Zhao X, Bai Q (2018) Simulation and stability analysis of conflict events between employees and organization based on the social network. Concurrency and Computation: Practice and Experience, p e5097
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, Y., Liu, Y., Ma, X. et al. Community detection in signed networks by relaxing modularity optimization with orthogonal and nonnegative constraints. Neural Comput & Applic 32, 10645–10654 (2020). https://doi.org/10.1007/s00521-019-04597-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-019-04597-9