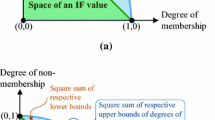
Abstract
This paper extends one of the most extensively used multiple criteria decision analysis (MCDA) methods, the technique for order preference by similarity to ideal solutions (TOPSIS), to adapt to highly complicated uncertain environments based on interval-valued Pythagorean fuzzy (IVPF) sets. In contrast to classical TOPSIS methods, this paper develops a novel concept of Pearson-like IVPF correlation coefficients instead of distance measures to not only construct a useful and effective association measure between two IVPF characteristics but also depict the outranking relationship of IVPF information. Moreover, this paper proposes the (weighted) IVPF correlation-based closeness coefficients to establish a Pearson-like correlation-based TOPSIS model to manage MCDA problems within the IVPF environment. In particular, there is a definite improvement in determining the closeness coefficient required in the TOPSIS procedure. This paper considers anchored judgments with respect to the positive- and negative-ideal IVPF solutions and provides new approach- and avoidance-oriented definitions for the IVPF correlation-based closeness coefficient, which is entirely different from the traditional definition of relative closeness in TOPSIS. Furthermore, this paper proposes a comprehensive IVPF correlation-based closeness index to balance the consequences between ultra-approach orientation and ultra-avoidance orientation and acquire the ultimate compromise solution for decision support and aid. The feasibility and practicability of the developed methodology are illustrated by a practical MCDA problem of rehabilitation treatment for hospitalized patients with acute stroke. The application results, along with experimentations and comparative analyses, demonstrate that the developed methods are rational and effective.





Similar content being viewed by others
References
Ang YH, Chan DK, Heng DM, Shen Q (2003) Patient outcomes and length of stay in a stroke unit offering both acute and rehabilitation services. Med J Australia 178(7):333–336
Biswas A, Sarkar B (2019) Interval-valued Pythagorean fuzzy TODIM approach through point operator-based similarity measures for multicriteria group decision making. Kybernetes 48(3):496–519
Cabrerizo FJ, Ureña MR, Pedrycz W, Herrera-Viedma E (2014) Building consensus in group decision making with an allocation of information granularity. Fuzzy Sets Syst 255:115–127
Cayir Ervural B, Zaim S, Demirel OF, Aydin Z, Delen D (2018) An ANP and fuzzy TOPSIS-based SWOT analysis for Turkey’s energy planning. Renew Sustain Energy Rev 82(1):1538–1550
Chen T-Y (2018) A novel risk evaluation method of technological innovation using an inferior ratio-based assignment model in the face of complex uncertainty. Expert Syst Appl 95:333–350
Chen T-Y (2018) A novel VIKOR method with an application to multiple criteria decision analysis for hospital-based post-acute care within a highly complex uncertain environment. Neural Comput Appl 1:11. https://doi.org/10.1007/s00521-017-3326-8
Chen T-Y (2019) Multiple criteria decision analysis under complex uncertainty: a Pearson-like correlation-based Pythagorean fuzzy compromise approach. Int J Intell Syst 34(1):114–151
Çoban V, Onar SÇ (2018) Pythagorean fuzzy engineering economic analysis of solar power plants. Soft Comput 22(15):5007–5020
Du Y, Hou F, Zafar W, Yu Q, Zhai Y (2017) A novel method for multiattribute decision making with interval-valued Pythagorean fuzzy linguistic information. Int J Intell Syst 32(10):1085–1112
Dwivedi G, Srivastava RK, Srivastava SK (2018) A generalised fuzzy TOPSIS with improved closeness coefficient. Expert Syst Appl 96:185–195
Farajpour F, Yousefli A (2018) Information flow in supply chain: a fuzzy TOPSIS parameters ranking. Uncertain Supply Chain Manag 6(2):181–194
Garg H (2017) A novel improved accuracy function for interval valued Pythagorean fuzzy sets and its applications in the decision-making process. Int J Intell Syst 32(12):1247–1260
Garg H (2018) Generalised Pythagorean fuzzy geometric interactive aggregation operators using Einstein operations and their application to decision making. J Exp Theor Artif Intell 30(6):763–794
Gul M, Ak MF (2018) A comparative outline for quantifying risk ratings in occupational health and safety risk assessment. J Clean Prod 196:653–664
Guleria A, Bajaj RK (2018) On Pythagorean fuzzy soft matrices, operations and their applications in decision making and medical diagnosis. Soft Comput 1:11. https://doi.org/10.1007/s00500-018-3419-z
Hwang C-L, Lai Y-J, Liu T-Y (1993) A new approach for multiple objective decision making. Comput Oper Res 20(8):889–899
Hwang C-L, Yoon K (1981) Multiple attribute decision making: methods and applications. Springer, Berlin
Khan F, Khan MSA, Shahzad M, Abdullah S (2019) Pythagorean cubic fuzzy aggregation operators and their application to multi-criteria decision making problems. J Intell Fuzzy Syst 36(1):595–607
Langhorne P, Pollock A (2002) What are the components of effective stroke unit care? Age Aging 31(5):365–371
Liang D, Darko AP, Xu Z, Quan W (2018) The linear assignment method for multicriteria group decision making based on interval-valued Pythagorean fuzzy Bonferroni mean. Int J Intell Syst 33(11):2101–2138
Liang D, Xu Z (2017) The new extension of TOPSIS method for multiple criteria decision making with hesitant Pythagorean fuzzy sets. Appl Soft Comput 60:167–179
Liang D, Xu Z, Liu D, Wu Y (2018) Method for three-way decisions using ideal TOPSIS solutions at Pythagorean fuzzy information. Inf Sci 435:282–295
Liang W, Zhang X, Liu M (2015) The maximizing deviation method based on interval-valued Pythagorean fuzzy weighted aggregating operator for multiple criteria group decision analysis. Discrete Dyn Nat Soc 2015, Article ID 746572: 15 pages. http://dx.doi.org/10.1155/2015/746572
Liao H, Xu Z, Herrera-Viedma E, Herrera F (2018) Hesitant fuzzy linguistic term set and its application in decision making: a state-of-the-art survey. Int J Fuzzy Syst 20(7):2084–2110
Lin Y-L, Ho L-H, Yeh S-L, Chen T-Y (2019) A Pythagorean fuzzy TOPSIS method based on novel correlation measures and its application to multiple criteria decision analysis of inpatient stroke rehabilitation. Int J Comput Intell Syst 12(1):410–425
Liu Y, Qin Y, Han Y (2018) Multiple criteria decision making with probabilities in interval-valued Pythagorean fuzzy setting. Int J Fuzzy Syst 20(2):558–571
Massanet S, Riera JV, Torrens J, Herrera-Viedma E (2014) A new linguistic computational model based on discrete fuzzy numbers for computing with words. Inf Sci 258:277–290
Nguyen VQ, PrvuBettger J, Guerrier T, Hirsch MA, Thomas JG, Pugh TM, Rhoads CF (2015) Factors associated with discharge to home versus discharge to institutional care after inpatient stroke rehabilitation. Arch Phys Med Rehabil 96(7):1297–1303
Nie R-X, Tian Z-P, Wang J-Q, Hu J-H (2019) Pythagorean fuzzy multiple criteria decision analysis based on Shapley fuzzy measures and partitioned normalized weighted Bonferroni mean operator. Int J Intell Syst 34(2):297–324
Peng X, Li W (2019) Algorithms for interval-valued Pythagorean fuzzy sets in emergency decision making based on multiparametric similarity measures and WDBA. IEEE Access 7:7419–7441
Peng X, Yang Y (2016) Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int J Intell Syst 31(5):444–487
Rahman K, Ali A, Abdullah S, Amin F (2018) Approaches to multi-attribute group decision making based on induced interval-valued Pythagorean fuzzy Einstein aggregation operator. New Math Nat Comput 14(3):343–361
Rahman K, Khan MA, Ullah M, Fahmi A (2017) Multiple attribute group decision making for plant location selection with Pythagorean fuzzy weighted geometric aggregation operator. Nucleus 54(1):66–74
Rice DB, McIntyre A, Mirkowski M, Janzen S, Viana R, Britt E, Teasell R (2017) Patient-centered goal setting in a hospital-based outpatient stroke rehabilitation center. PM & R 9(9):856–865
Ringelstein EB, Chamorro A, Kaste M, Langhorne P, Leys D, Lyrer P, Thijs V, Thomassen L, Toni D (2013) European Stroke Organisation recommendations to establish a stroke unit and stroke center. Stroke 44(3):828–840
Sadic S, de Sousa JP, Crispim JA (2018) A two-phase MILP approach to integrate order, customer and manufacturer characteristics into dynamic manufacturing network formation and operational planning. Expert Syst Appl 96:462–478
Sangaiah AK, Gopal J, Basu A, Subramaniam PR (2017) An integrated fuzzy DEMATEL, TOPSIS, and ELECTRE approach for evaluating knowledge transfer effectiveness with reference to GSD project outcome. Neural Comput Appl 28(1):111–123
Sawabe M, Momosaki R, Hasebe K, Sawaguchi A, Kasuga S, Asanuma D, Suzuki S, Miyauchi N, Abo M (2018) Rehabilitation characteristics in high-performance hospitals after acute stroke. J Stroke Cerebrovasc Dis 27(9):2431–2435
Shen F, Ma X, Li Z, Xu Z, Cai D (2018) An extended intuitionistic fuzzy TOPSIS method based on a new distance measure with an application to credit risk evaluation. Inf Sci 428:105–119
Singh S, Garg H (2017) Distance measures between type-2 intuitionistic fuzzy sets and their application to multicriteria decision-making process. Appl Intell 46(4):788–799
Viswanathan A, Rakich SM, Engel C, Snider R, Rosand J, Greenberg SM, Smith EE (2006) Antiplatelet use after intracerebral hemorrhage. Neurology 66(2):206–209
Walczak D, Rutkowska A (2017) Project rankings for participatory budget based on the fuzzy TOPSIS method. Eur J Oper Res 260(2):706–714
Wan S-P, Li S-Q, Dong J-Y (2018) A three-phase method for Pythagorean fuzzy multi-attribute group decision making and application to haze management. Comput Ind Eng 123:348–363
Wan S-P, Qin Y-L, Dong J-Y (2017) A hesitant fuzzy mathematical programming method for hybrid multi-criteria group decision making with hesitant fuzzy truth degrees. Knowl Based Syst 138:232–248
Wu T, Liu X, Liu F (2018) An interval type-2 fuzzy TOPSIS model for large scale group decision making problems with social network information. Inf Sci 432:392–410
Xing Y, Zhang R, Wang J, Zhu X (2018) Some new Pythagorean fuzzy Choquet–Frank aggregation operators for multi-attribute decision making. Int J Intell Syst 33(11):2189–2215
Yager RR (2013) Pythagorean fuzzy subsets. In: Proceedings of the 2013 joint IFSA world congress and NAFIPS annual meeting, Edmonton, Canada, June 24–28, pp 57–61
Yager RR (2014) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965
Yager RR (2016) Properties and applications of Pythagorean fuzzy sets. In: Angelov P, Sotirov S (eds) Imprecision and uncertainty in information representation and processing, studies in fuzziness and soft computing, vol 332. Springer, Basel, pp 119–136
Yager RR, Abbasov AM (2013) Pythagorean membership grades, complex numbers, and decision making. Int J Intell Syst 28(5):436–452
Yilmazlar S, Abas F, Korfali E (2005) Comparison of ventricular drainage in poor grade patients after intracranial hemorrhage. Neurol Res 27(6):653–656
Yoon K (1987) A reconciliation among discrete compromise solutions. J Oper Res Soc 38(3):277–286
Yu C, Shao Y, Wang K, Zhang L (2019) A group decision making sustainable supplier selection approach using extended TOPSIS under interval-valued Pythagorean fuzzy environment. Expert Syst Appl 121:1–17
Zavadskas EK, Mardani A, Turskis Z, Jusoh A, Nor KM (2016) Development of TOPSIS method to solve complicated decision-making problems—an overview on developments from 2000 to 2015. Int J Inf Technol Decis Mak 15(3):645–682
Zeng S, Chen J, Li X (2016) A hybrid method for Pythagorean fuzzy multiple-criteria decision making. Int J Inf Technol Decis Mak 15(2):403–422
Zhang X (2016) Multicriteria Pythagorean fuzzy decision analysis: a hierarchical QUALIFLEX approach with the closeness index-based ranking methods. Inf Sci 330:104–124
Zhang X (2017) Pythagorean fuzzy clustering analysis: a hierarchical clustering algorithm with the ratio index-based ranking methods. Int J Intell Syst 33(9):1798–1822
Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29(12):1061–1078
Zhou J, Su W, Baležentis T, Streimikiene D (2018) Multiple criteria group decision-making considering symmetry with regards to the positive and negative ideal solutions via the Pythagorean normal cloud model for application to economic decisions. Symmetry 10(5):140. https://doi.org/10.3390/sym10050140
Zyoud SH, Fuchs-Hanusch D (2017) A bibliometric-based survey on AHP and TOPSIS techniques. Expert Syst Appl 78:158–181
Acknowledgements
The authors acknowledge the assistance of the respected editor and the anonymous referees for their insightful and constructive comments, which helped to improve the overall quality of the paper. The authors are grateful for grant funding support from the Taiwan Ministry of Science and Technology (MOST 105-2410-H-182-007-MY3) and Linkou Chang Gung Memorial Hospital (BMRP 574 and CMRPD2F0203) during the completion of this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflict of interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ho, LH., Lin, YL. & Chen, TY. A Pearson-like correlation-based TOPSIS method with interval-valued Pythagorean fuzzy uncertainty and its application to multiple criteria decision analysis of stroke rehabilitation treatments. Neural Comput & Applic 32, 8265–8295 (2020). https://doi.org/10.1007/s00521-019-04304-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-019-04304-8