Skip to main content
SpringerLink
Log in

A modified discrete antlion optimizer for the ring star problem with secondary sub-depots

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

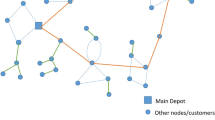
This paper introduces a new problem in the field of combinatorial optimization. This problem can be named as the ring star problem with secondary sub-depots (RSPSSD). RSPSSD has one fixed main depot, and it allows a network to be divided into three types of nodes, namely primary sub-depots (includes the main depot too), secondary sub-depots and left out nodes. The challenge of the problem is to select some primary and secondary sub-depots that minimize the total routing cost which has three components. The first one is the routing cost of the main circuit that covers all the primary sub-depots including the main depot. The second one is the total routing cost of all the secondary circuits, each of which covers a set of few secondary sub-depots and their nearest primary sub-depot. The secondary circuits also have a constraint on the number of secondary sub-depots in it. The last one is the assignment cost of the left out nodes to their nearest concentrators which is nothing but anyone from the main depot, primary or secondary sub-depots. The proposed RSPSSD problem is solved with the proposed modified discrete antlion optimizer and tested using some TSP benchmark instances. The random walk of an antlion and an ant is encoded with ternary number system. The statistical analysis and comparison of the result against some other algorithms are also presented. A real-life case study has also been shown to validate the proposed model and algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. http://www.discoveringdonana.com/wp-content/uploads/2016/06/hormiga-leon-larva-2.jpg.

  2. https://i.ytimg.com/vi/E76T8eKMVF8/maxresdefault.jpg.

References

  1. Baldacci R, Dell’Amico M (2010) Heuristic algorithms for the multi-depot ring star problem. Eur J Oper Res 203(1):270–281

    Article  Google Scholar 

  2. Baldacci R, Dell’Amico M, Salazar González JJ (2007) The capacitated m-ring star problem. Oper Res 55(6):1147–1162

    Article  MathSciNet  Google Scholar 

  3. Bodin P, Horton S (2004) Source parameters and tectonic implications of aftershocks of the \(M_w\) 7.6 Bhuj earthquake of 26 January 2001. Bull Seismol Soc Am 94(3):818–827

    Article  Google Scholar 

  4. Calvete HI, Galé C, Iranzo JA (2013) An efficient evolutionary algorithm for the ring star problem. Eur J Oper Res 231:22–33

    Article  MathSciNet  Google Scholar 

  5. Dias TCS, de Sousa Filho GF, Macambira EM, Cabral LAF, Fampa MHC (2006) An efficient heuristic for the ring star problem. In: Alvarez C, Serna M (eds) Experimental algorithms. Lecture notes in computer science. Springer, Berlin, pp 24–35 (No. 4007)

    Chapter  Google Scholar 

  6. Kedad-Sidhoum S, Nguyen VH (2010) An exact algorithm for solving the ring star problem. Optimization 59(1):125–140

    Article  MathSciNet  Google Scholar 

  7. Labbe M, Laporte G, Rodriguez Martin I, Salazar Gonzalez JJ (2004) The ring star problem: polyhedral analysis and exact algorithm. Networks 43(3):177–189

    Article  MathSciNet  Google Scholar 

  8. Labbe M, Laporte G, Rodriguez Martin I, Salazar Gonzalez JJ (1999) The median cycle problem. Working paper, CRT-99-29, Université de Montréal

  9. Mirjalili S (2015) The ant lion optimizer. Adv Eng Softw 83:80–98

    Article  Google Scholar 

  10. Mirjalili S, Jangir P, Saremi S (2016) Multi-objective ant lion optimizer: a multiobjective optimization algorithm for solving engineering problems. Appl Intell 45(1):79–95

    Article  Google Scholar 

  11. Moreno Perez JA, Moreno Vega JM, Rodriguez Martin I (2003) Variable neighborhood tabu search and its application to the median cycle problem. Eur J Oper Res 151(2):365–378

    Article  MathSciNet  Google Scholar 

  12. Naji-Azimi Z, Salari M, Toth P (2012) An integer linear programming based heuristic for the capacitated m-ring-star problem. Eur J Oper Res 217(1):17–25

    Article  MathSciNet  Google Scholar 

  13. Rikalovic A, Soares GA, Ignjatic J (2018) Spatial analysis of logistics center location: a comprehensive approach. Decis Mak Appl Manag Eng 1(1):38–50. https://doi.org/10.31181/dmame180138r

    Article  Google Scholar 

  14. Simonetti L, Frota Y, de Souza CC (2011) The ring-star problem: a new integer programming formulation and a branch-and-cut algorithm. Discrete Appl Math 159(16):1901–1914

    Article  MathSciNet  Google Scholar 

  15. Sinha A (2016) The Gujarat earthquake 2001, Asian Disaster Reduction Center. Asian Disaster Reduction Center. Retrieved 20 July 2016

  16. TSPLIB. http://elib.zib.de/pub/mp-testdata/tsp/tsplib/tsp

  17. web: http://distancecalculator.globefeed.com

  18. web: http://vassarstats.net/wilcoxon.html

  19. web: http://www.gujaratplus.com/earthquake/vil_situat.htm

  20. Yang J, Shi X, Marchese Y, Liang Y (2008) An ant colony optimization method for generalized TSP problem. Prog Nat Sci 18:1417–1422

    Article  MathSciNet  Google Scholar 

  21. Yogaranjan G, Revathi T (2016) A discrete ant lion optimization (DALO) algorithm for solving data gathering tour problem in wireless sensor networks. Middle-East J Sci Res 24(10):3113–3120

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Durgapur, Durgapur, West Bengal, 713209, India

    Anupam Mukherjee, Goutam Panigrahi & Samarjit Kar

  2. Department of Computer Science, NSHM Knowledge Campus, Durgapur, West Bengal, 713212, India

    Partha Sarathi Barma & Joydeep Dutta

  3. Department of Applied Mathematics, Vidyasagar University, Midnapore, West Bengal, 721102, India

    Manoranjan Maiti

Authors
  1. Anupam Mukherjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Partha Sarathi Barma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Joydeep Dutta
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Goutam Panigrahi
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Samarjit Kar
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Manoranjan Maiti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Samarjit Kar.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mukherjee, A., Barma, P.S., Dutta, J. et al. A modified discrete antlion optimizer for the ring star problem with secondary sub-depots. Neural Comput & Applic 32, 8143–8156 (2020). https://doi.org/10.1007/s00521-019-04292-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-019-04292-9

Keywords

Search

Navigation