Skip to main content
SpringerLink
Log in

A new comprehensive possibilistic group decision approach for resilient supplier selection with mean–variance–skewness–kurtosis and asymmetric information under interval-valued fuzzy uncertainty

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

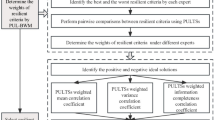
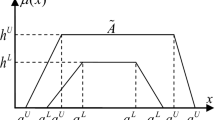
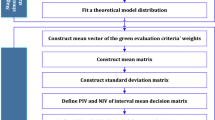
Since resilient supplier selection problems (RSSPs) are regarded vague, uncertain and complex, interval-valued fuzzy sets (IVFSs) and possibilistic statistical theories can assist to deal with preferences and experience of group of experts into meaningful results to appraise the potential suppliers. This research presents a novel comprehensive possibilistic statistical group decision approach with IVFSs and asymmetric information to solve RSSPs in the supply chain networks (SCNs). Possibilistic statistical concepts, including mean, variance, skewness and kurtosis, are proposed for the first time in the literature of SCNs for the group decision process. Also, asymmetric information with IVFSs is provided in the presented approach along with introducing two new extensions of weighting methods for experts as well as evaluation criteria. In addition, new relations, new separation measures and novel distinguish indices are introduced regarding to the preference by similarity to ideal solutions with mean–variance–skewness–kurtosis modeling. Then, the proposed comprehensive decision approach is implemented to an application in automobile industry for the RSSPs to assess the resilience strategy in the SCNs under uncertain conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Azadfallah M (2016) Improving preference assessment in TOPSIS method for multi-criteria supplier selection problem. Int J Supply Chain Oper Resil 2(3):233–245

    Article  Google Scholar 

  2. Baležentis T, Baležentis A (2014) A survey on development and applications of the multi-criteria decision making method multimoora. J Multi-Criteria Decision Anal 21(3–4):209–222

    Article  Google Scholar 

  3. Chai J, Liu JN, Ngai EW (2013) Application of decision-making techniques in supplier selection: a systematic review of literature. Expert Syst Appl 40(10):3872–3885

    Article  Google Scholar 

  4. Chang KH (2017) A novel supplier selection method that integrates the intuitionistic fuzzy weighted averaging method and a soft set with imprecise data. Ann Oper Res. https://doi.org/10.1007/s10479-017-2718-6

    Article  Google Scholar 

  5. Deng Y, Chan FT, Wu Y, Wang D (2011) A new linguistic MCDM method based on multiple-criterion data fusion. Expert Syst Appl 38(6):6985–6993

    Article  Google Scholar 

  6. Deng Y, Sadiq R, Jiang W, Tesfamariam S (2011) Risk analysis in a linguistic environment: a fuzzy evidential reasoning-based approach. Expert Syst Appl 38(12):15438–15446

    Article  Google Scholar 

  7. Ebrahimnejad S, Mousavi SM, Tavakkoli-Moghaddam R, Heydar M (2014) Risk ranking in mega projects by fuzzy compromise approach: a comparative analysis. J Intell Fuzzy Syst 26:949–959

    MathSciNet  MATH  Google Scholar 

  8. Foroozesh N, Tavakkoli-Moghaddam R, Mousavi SM (2017) Resilient supplier selection in a supply chain by a new interval-valued fuzzy group decision model based on possibilistic statistical concepts. J Ind Syst Eng 10(2):113–133

    Google Scholar 

  9. Gitinavard H, Mousavi SM, Vahdani B (2017) Soft computing-based new interval-valued hesitant fuzzy multi-criteria group assessment method with last aggregation to industrial decision problems. Soft Comput 21(12):3247–3265

    Article  MATH  Google Scholar 

  10. Gitinavard H, Mousavi SM, Vahdani B (2017) Soft computing based on hierarchical evaluation approach and criteria interdependencies for energy decision-making problems: a case study. Energy 118:556–577

    Article  Google Scholar 

  11. Haldar A, Ray A, Banerjee D, Ghosh S (2012) A hybrid MCDM model for resilient supplier selection. Int J Manag Sci Eng Manag 7(4):284–292

    Google Scholar 

  12. Haldar A, Ray A, Banerjee D, Ghosh S (2014) Resilient supplier selection under a fuzzy environment. Int J Manag Sci Eng Manag 9(2):147–156

    Google Scholar 

  13. Hosseini S (2016) Modeling and measuring resilience: applications in supplier selection and critical infrastructure. https://shareok.org/handle/11244/44886. Accessed 1 Aug 2016

  14. Hosseini S, Al Khaled A (2016) A hybrid ensemble and AHP approach for resilient supplier selection. J Intell Manuf. https://doi.org/10.1007/s10845-016-1241-y

    Article  Google Scholar 

  15. Hosseini S, Barker K (2016) A Bayesian network model for resilience-based supplier selection. Int J Prod Econ 180:68–87

    Article  Google Scholar 

  16. Junior FRL, Osiro L, Carpinetti LCR (2014) A comparison between fuzzy AHP and fuzzy TOPSIS methods to supplier selection. Appl Soft Comput 21:194–209

    Article  Google Scholar 

  17. Kamdem JS, Deffo CT, Fono LA (2012) Moments and semi-moments for fuzzy portfolio selection. Insur Math Econ 51(3):517–530

    Article  MathSciNet  MATH  Google Scholar 

  18. Kuo MS, Liang GS (2012) A soft computing method of performance evaluation with MCDM based on interval-valued fuzzy numbers. Appl Soft Comput 12(1):476–485

    Article  Google Scholar 

  19. Mohagheghi V, Mousavi SM, Vahdani B (2015) A new optimization model for project portfolio selection under interval-valued fuzzy environment. Arab J Sci Eng 40:3351–3361

    Article  MathSciNet  MATH  Google Scholar 

  20. Mohagheghi V, Mousavi SM, Vahdani B (2016) A new multi-objective optimization approach for sustainable project portfolio selection: a real-world application under interval-valued fuzzy environment. Iran J Fuzzy Syst 13(6):41–68

    MathSciNet  Google Scholar 

  21. Parkouhi SV, Ghadikolaei AS (2017) A resilience approach for supplier selection: using fuzzy analytic network process and grey VIKOR techniques. J Clean Prod 161:431–451

    Article  Google Scholar 

  22. Pettit TJ, Fiksel J, Croxton KL (2010) Ensuring supply chain resilience: development of a conceptual framework. J Bus Logist 31(1):1–21

    Article  Google Scholar 

  23. Ponomarov SY, Holcomb MC (2009) Understanding the concept of supply chain resilience. Int J Logist Manag 20(1):124–143

    Article  Google Scholar 

  24. Pramanik D, Haldar A, Mondal SC, Naskar SK, Ray A (2017) Resilient supplier selection using AHP-TOPSIS-QFD under a fuzzy environment. Int J Manag Sci Eng Manag 12(1):45–54

    Google Scholar 

  25. Rajagopal V, Venkatesan SP, Goh M (2017) Decision-making models for supply chain risk mitigation: a review. Comput Ind Eng 113:646–682

    Article  Google Scholar 

  26. Rajesh R, Ravi V (2015) Supplier selection in resilient supply chains: a grey relational analysis approach. J Clean Prod 86:343–359

    Article  Google Scholar 

  27. Sahu AK, Datta S, Mahapatra SS (2016) Evaluation and selection of resilient suppliers in fuzzy environment: exploration of fuzzy-VIKOR. Benchmark Int J 23(3):651–673

    Article  Google Scholar 

  28. Sanayei A, Mousavi SF, Yazdankhah A (2010) Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Syst Appl 37(1):24–30

    Article  Google Scholar 

  29. Sheffi Y (2006) Resilience reduces risk. Logist Q 12(1):12–14

    Google Scholar 

  30. Shemshadi A, Shirazi H, Toreihi M, Tarokh MJ (2011) A fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting. Expert Syst Appl 38(10):12160–12167

    Article  Google Scholar 

  31. Vahdani B, Mousavi SM, Ebrahimnejad S (2014) Soft computing-based preference selection index method for human resource management. J Intell Fuzzy Syst 26(1):393–403

    MathSciNet  MATH  Google Scholar 

  32. Vahdani B, Mousavi SM, Tavakkoli-Moghaddam R, Ghodratnama A, Mohammadi M (2014) Robot selection by a multiple criteria complex proportional assessment method under an interval-valued fuzzy environment. Int J Adv Manuf Technol 73(5–8):687–697

    Article  Google Scholar 

  33. Wang JW, Cheng CH, Huang KC (2009) Fuzzy hierarchical TOPSIS for supplier selection. Appl Soft Comput 9(1):377–386

    Article  Google Scholar 

  34. Wang X, Herty M, Zhao L (2016) Contingent rerouting for enhancing supply chain resilience from supplier behavior perspective. Int Trans Oper Res 23(4):775–796

    Article  MathSciNet  MATH  Google Scholar 

  35. Yeh Tsu-Ming, Pai Fan-Yun, Liao Cheng-Wei (2014) Using a hybrid MCDM methodology to identify critical factors in new product development. Neural Comput Appl 24(3–4):957–971

    Article  Google Scholar 

  36. Zimmermann HJ (2001) Fuzzy set theory and its applications, 4th edn. Springer, Dordrecht

    Book  Google Scholar 

Download references

Acknowledgements

The authors are grateful to four anonymous referees for their valuable suggestions and comments that improved the quality of the primary version.

Author information

Authors and Affiliations

  1. School of Industrial Engineering, College of Engineering, University of Tehran, Tehran, Iran

    N. Foroozesh & R. Tavakkoli-Moghaddam

  2. Laboratoire de Conception, Fabrication Commande, Arts et Métier Paris Tech, Centre de Metz, Metz, France

    R. Tavakkoli-Moghaddam

  3. Department of Industrial Engineering, Faculty of Engineering, Shahed University, Tehran, Iran

    S. Meysam Mousavi

  4. Department of Industrial Engineering, Faculty of Industrial and Mechanical Engineering, Qazvin Branch, Islamic Azad University, Qazvin, Iran

    B. Vahdani

Authors
  1. N. Foroozesh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Tavakkoli-Moghaddam
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Meysam Mousavi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. B. Vahdani
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The authors of this research confirm their names’ arrangement based on their contributions in the revised version.

Corresponding author

Correspondence to N. Foroozesh.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Foroozesh, N., Tavakkoli-Moghaddam, R., Mousavi, S.M. et al. A new comprehensive possibilistic group decision approach for resilient supplier selection with mean–variance–skewness–kurtosis and asymmetric information under interval-valued fuzzy uncertainty. Neural Comput & Applic 31, 6959–6979 (2019). https://doi.org/10.1007/s00521-018-3506-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-018-3506-1

Keywords

Search

Navigation