Abstract
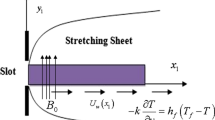
The present study emphases on the three-dimensional (3D) Casson nanofluid flow across a slendering sheet in porous layers by considering the thermophoresis and Brownian motion effect. The proposed mathematical model has a tendency to characterise the effect of the non-uniform heat source/sink. In the present simulation, the graphene–water-based nanoparticles have been used at two different temperatures namely 10 and 50 °C. The nonlinear ordinary differential equations are solved using the Runge–Kutta Feldberg integration method. The characteristics of velocity, temperature and concentration boundary layers in the presence of graphene–water nanoparticles are presented for different physical parameters such as heat source/sink parameter, thermophoresis parameter, Brownian motion parameter, Casson fluid parameter, porosity parameter, volume fraction and velocity power index parameter. Moreover, the friction factor coefficients, Nusselt number and Sherwood number are also estimated and discussed for aforesaid physical parameters. It is found that there is a significant increase in the thermal and concentration boundary layer thickness when the strength of the thermophoresis parameter is increased. In contrast, thermal boundary layer increases with the rise in the Brownian motion parameter, while the reverse trend holds true for concentration field. In addition, the rate of heat and mass transfer rate are higher in case of graphene–water nanoparticle at 50 °C compared to 10 °C temperature.
















Similar content being viewed by others
Abbreviations
- u, v, w :
-
Velocity components in x, y and z directions
- C p :
-
Specific heat capacity at constant pressure
- f, g :
-
Dimensionless velocities
- A :
-
Coefficient related to stretching sheet
- m :
-
Velocity power index parameter
- B(x):
-
Magnetic field parameter
- T :
-
Temperature of the fluid
- k :
-
Thermal conductivity
- D m :
-
Molecular diffusivity of the species concentration
- C s :
-
Concentration susceptibility
- C :
-
Concentration of the fluid
- T m :
-
Mean fluid temperature
- T ∞ :
-
Temperature of the fluid in the free stream
- C ∞ :
-
Concentration of the fluid in the free stream
- \(j_{1}^{*}\) :
-
Dimensional velocity slip parameter
- \(j_{2}^{*}\) :
-
Dimensional temperature jump parameter
- \(j_{3}^{*}\) :
-
Dimensional concentration jump parameter
- f 1 :
-
Maxwell’s reflection coefficient
- a :
-
Thermal accommodation coefficient
- b :
-
Physical parameter related to stretching sheet
- d :
-
Concentration accommodation coefficient
- m :
-
Velocity power index parameter
- Pr :
-
Prandtl number
- q′′′:
-
Non-uniform heat source/sink parameter
- B(x):
-
Dimensional magnetic field parameter
- M :
-
Magnetic interaction parameter
- K :
-
Porosity parameter
- Nt:
-
Thermophoresis parameter
- Le :
-
Lewis number
- Nb:
-
Brownian motion parameter
- j 1 :
-
Dimensionless velocity slip parameter
- j 2 :
-
Dimensionless temperature jump parameter
- j 3 :
-
Dimensionless concentration jump parameter
- C f :
-
Wall skin friction coefficient
- Nu x :
-
Local Nusselt number
- Sh x :
-
Local Sherwood number
- Re x :
-
Local Reynolds number
- ϕ :
-
Dimensionless concentration
- η :
-
Similarity variable
- σ :
-
Electrical conductivity of the fluid
- γ :
-
Ratio of specific heats
- θ :
-
Dimensionless temperature
- ρ nf :
-
Density of the nanofluid
- k nf :
-
Thermal conductivity of the nanofluid
- μ nf :
-
Dynamic viscosity of nanofluid
- υ f :
-
Kinematic viscosity
- δ :
-
Wall thickness parameter
- ξ 1, ξ 2 :
-
Mean free path (constant)
- ξ 3, ξ 4 :
-
Mean free path (constant)
- Γ:
-
Positive characteristic time
References
Lee SW, Lee SS, Yang EH (2009) A study on field emission characteristics of planar graphene layers obtained from a highly oriented pyrolyzed graphite bloc. Nanoscale Res Lett 4:1218–1221
Malesevic A, Kemps R, Vanhulsel A, Chowdhury PM, Alexander V, Chris VH (2008) Field emission from vertically aligned few-layer graphene. J Appl Phys 104:084301
Mao LF (2011) A theoretical analysis of field emission from graphene nanoribbons. Carbon 49(8):2709–2714
Haque AKMM, Kwon S, Kim J, Noh J, Huh S, Chung H, Jeong H (2015) An experimental study on thermal characteristics of nanofluid with graphene and multi-wall carbon nanotubes. J Cent South Univ 22:3202–3210
Baby TT, Prabhu SR (2012) Experimental study on the field emission properties of metal oxide nanoparticle–decorated graphene. J Appl Phys 111:034311
Bhargava R, Goyal M (2014) MHD non-Newtonian nanofluid flow over a permeable stretching sheet with heat generation and velocity slip. Int J Math Comput Nat Phys Eng 8(6):910–916
Cortell R (2014) MHD (magneto-hydrodynamic) flow and radiative nonlinear heat transfer of a viscoelastic fluid over a stretching sheet with heat generation/absorption. Energy 74:896–905
Raju CSK, Sandeep N, Sugunamma V, Babu MJ, Reddy JVR (2016) Heat and mass transfer in magnetohydrodynamic Casson fluid over an exponentially permeable stretching surface. Eng Sci Technol Int J 19(1):45–52
Hayat T, Imtiaz M, Alsaedi A, Kutbi MA (2015) MHD three dimensional flow of nanofluid with velocity slip and nonlinear thermal radiation. J Magn Magn Mater 396:31–37
Animasaun IL, Raju CSK, Sandeep N (2016) Unequal diffusivities case of homogeneous–heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation. Alex Eng J 55(2):1595–1606
Nelson E (1967) Dynamical theories of Brownian motion, vol 3. Princeton University Press, Princeton
Nadeem S, Haq RU, Akbar NS (2014) MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans Nanotechnol 13(1):109–115
Raju CSK, Hoque MM, Anika NN, Mamatha SU, Sharma P (2017) Natural convective heat transfer analysis of MHD unsteady Carreau nanofluid over a cone packed with alloy nanoparticles. Powder Technol 317:408–416
Raju CSK, Hoque MM, Sivasankar T (2016) Radiative flow of Casson fluid over a moving wedge filled with gyrotactic microorganisms. Adv Powder Technol 28(2):575–583
Raju CSK, Sandeep N (2016) Unsteady three-dimensional flow of Casson–Carreau fluids past a stretching surface. Alex Eng J 55(2):1115–1126
Beg OA, Hoque MM, Wahiduzzaman M, Alam MM, Ferdows M (2014) Spectral numerical simulation of mageneto-physiological laminar Dean flow. J Mech Med Biol 14(4):1450047
Hoque MM, Alam MM (2013) Effects of Dean number and curvature on fluid flow through a curved pipe with magnetic field. Procedia Eng 56:243–253
Hoque MM, Alam MM, Ferdows M, Beg OA (2013) Numerical simulation of Dean number and curvature effects on magneto-bio-fluid flow through a curved conduit. Proc Inst Mech Eng H J Eng Med 227(11):1155–1170
Hoque MM, Anika NN, Alam MM (2013) Numerical analysis of magnetohydrodynamics flow in a curved duct. Int J Sci Eng Res 4(7):607–617
Hoque MM, Alam MM (2015) A numerical study of MHD laminar flow in a rotating curved pipe with circular cross section. Open J Fluid Dyn 5:121–127
Hoque MM, Anika NN, Alam MM (2013) Magnetic effects on direct numerical solution of fluid flow through a curved pipe with circular cross section. Eur J Sci Res 103(3):343–361
Reddy GJ, Kethireddy B, Kumar M, Hoque MM (2018) A molecular dynamics study on transient non-Newtonian MHD Casson fluid flow dispersion over a radiative vertical cylinder with entropy heat generation. J Mol Liq 252:245–262
Sulochana C, Ashwinkumar GP, Sandeep N (2016) Similarity solution of 3D Casson nanofluid flow over a stretching sheet with convective boundary conditions. J Niger Math Soc 35:128–141
Babu MJ, Sandeep N (2016) 3D MHD slip flow of a nanofluid over a slendering stretching sheet with thermophoresis and Brownian motion effects. J Mol Liq 222:1003–1009
Sandeep N, Koriko OK, Animasaun IL (2016) Modified kinematic viscosity model for 3D Casson fluid flow within boundary layer formed on a surface at absolute zero. J Mol Liq 221:1197–1206
Choi SUS (1995) Enhancing thermal conductivity of fluids with nanoparticles. Paper presented at the international mechanical engineering congress and exposition, San Francisco, USA
Buongiorno J (2005) Convective transport in nanofluids. J Heat Transf 128(3):240–250
Gireesha BJ, Mahanthesh B, Rashidi MM (2015) MHD boundary layer heat and mass transfer of a chemically reacting Casson fluid over a permeable stretching surface with non-uniform heat source/sink. Int J Ind Math 7:247–260
Sheikholeslami M, Ganji DD (2015) Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Comput Methods Appl Mech Eng 283:651–663
Malvandi A, Heysiattalab S, Ganji DD (2016) Thermophoresis and Brownian motion effects on heat transfer enhancement at film boiling of nanofluids over a vertical cylinder. J Mol Liq 216:503–509
Fani B, Kalteh M, Abbassi A (2015) Investigating the effect of Brownian motion and viscous dissipation on the nanofluid heat transfer in a trapezoidal micro channel heat sink. Adv Powder Technol 26:83–90
Angayarkanni SA, Philip J (2015) Review on thermal properties of nanofluids: recent developments. Adv Colloid Interface Sci 225:146–176
Khan WA, Aziz A (2011) Natural convection flow of a nanofluid over a vertical plate with uniform surface heat flux. Int J Therm Sci 50(7):1207–1214
Kim J, Kang YT, Choi CK (2004) Analysis of convective instability and heat transfer characteristics of nanofluids. Phys Fluids 16:2395–2401
Sheikholeslami M (2017) Numerical simulation of magnetic nanofluid natural convection in porous media. Phys Lett A 381(5):494–503
Sheikholeslami M (2017) Influence of Lorentz forces on nanofluid flow in a porous cylinder considering Darcy model. J Mol Liq 225:903–912
Sheikholeslami M (2017) Magnetic field influence on nanofluid thermal radiation in a cavity with tilted elliptic inner cylinder. J Mol Liq 229:137–147
Sheikholeslami M (2017) Magnetohydrodynamic nanofluid forced convection in a porous lid driven cubic cavity using Lattice Boltzmann method. J Mol Liq 231:555–565
Sheikholeslami M (2017) Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann method. J Mol Liq 234:364–374
Sheikholeslami M, Rokni HB (2017) Nanofluid two phase model analysis in existence of induced magnetic field. Int J Heat Mass Transf 107:288–299
Sheikholeslamia M, Bhattib MM (2017) Active method for nanofluid heat transfer enhancement by means of EHD. Int J Heat Mass Transf 109:115–122
Sheikholeslamia M, Hayat T, Alsaedic A (2017) Numerical study for external magnetic source influence on water based nanofluid convective heat transfer. Int J Heat Mass Transf 106:745–755
Sheikholeslamia M, Shehzadb SA (2017) Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. Int J Heat Mass Transf 106:1261–1269
Sheikholeslamia M, Shehzadb SA (2017) Thermal radiation of ferrofluid in existence of Lorentz forces considering variable viscosity. Int J Heat Mass Transf 109:82–92
Khader M, Megahed AM (2003) Numerical solution for boundary layer flow due to a nonlinearly stretching sheet with variable thickness and slip velocity. Eur Phys J Plus 128:100–108
Devi SPA, Prakash M (2016) Slip flow effects over hydromagnetic forced convective flow over a slendering stretching sheet. J Appl Fluid Mech 9(2):683–692
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this paper.
Rights and permissions
About this article
Cite this article
Durgaprasad, P., Varma, S.V.K., Hoque, M.M. et al. Combined effects of Brownian motion and thermophoresis parameters on three-dimensional (3D) Casson nanofluid flow across the porous layers slendering sheet in a suspension of graphene nanoparticles. Neural Comput & Applic 31, 6275–6286 (2019). https://doi.org/10.1007/s00521-018-3451-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-018-3451-z