Skip to main content
SpringerLink
Log in

Synchronization of single-degree-of-freedom oscillators via neural network based on fixed-time terminal sliding mode control scheme

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

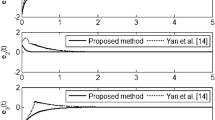
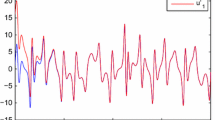
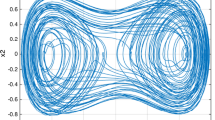
In this paper, the synchronization problem is investigated for two single-degree-of-freedom oscillators via neural network based on fixed-time terminal sliding mode control. First, a fixed-time terminal sliding mode is constructed. Then, in order to deal with the unknown function in master system, the neural network technique is introduced. Combining fixed-time terminal sliding mode surface and adaptive control scheme plus neural network technique, an adaptive fixed-time terminal sliding mode controller is presented. The stability of the closed-loop system is analyzed. Finally, simulation results are provided to demonstrate the effectiveness of the proposed two control strategies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Chung SJ, Slotine JJE (2009) Cooperative robot control and concurrent synchronization of Lagrangian systems. IEEE Trans Rob 25(3):686–700

    Article  Google Scholar 

  2. Du HB, Li SH (2014) Attitude synchronization control for a group of flexible spacecraft. Automatica 50(2):646–651

    Article  MathSciNet  Google Scholar 

  3. Zhang Z, Shen H, Li J (2011) Adaptive stabilization of uncertain unified chaotic systems with nonlinear input. Appl Math Comput 218(8):4260–4267

    MathSciNet  MATH  Google Scholar 

  4. Jia Q (2007) Adaptive control and synchronization of a new hyperchaotic system with unknown parameters. Phys Lett A 362(5–6):424–429

    Article  Google Scholar 

  5. Li R, Xu W, Li S (2009) Anti-synchronization on autonomous and non-autonomous chaotic systems via adaptive feedback control. Chaos Solitons Fractals 40(3):1288–1296

    Article  MathSciNet  Google Scholar 

  6. Li HQ, Liao XF, Li CD, Li CJ (2011) Chaos control and synchronization via a novel chatter free sliding mode control strategy. Neurocomputing 74(17):3212–3222

    Article  Google Scholar 

  7. Li HQ, Liao XF, Chen G, Hill DJ, Dong ZY, Huang TW (2015) Event-triggered asynchronous intermittent communication strategy for synchronization in complex dynamical networks. Neural Netw 66:1–10

    Article  Google Scholar 

  8. Li CJ, Gao DY, Liu C, Chen G (2014) Impulsive control for synchronizing delayed discrete complex networks with switching topology. Neural Comput Appl 24(1):59–68

    Article  Google Scholar 

  9. Li CJ, Yu XH, Huang TW, He X (2017) Distributed optimal consensus over resource allocation network and its application to dynamical economic dispatch. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2017.2691760

    Article  Google Scholar 

  10. Li CJ, Yu XH, Yu WW, Huang TW, Liu ZW (2016) Distributed event-triggered scheme for economic dispatch in smart grids. IEEE Trans Ind Inf 12(5):1775–1785

    Article  Google Scholar 

  11. Lei Y, Xu W, Shen J, Fang T (2006) Global synchronization of two parametrically excited systems using active control. Chaos Solitons Fractals 28(2):428–436

    Article  MathSciNet  Google Scholar 

  12. Wu XF, Cai JP, Wang MH (2008) Global chaos synchronization of the parametrically excited Duffing oscillators by linear state error feedback control. Chaos Solitons Fractals 36(1):121–128

    Article  MathSciNet  Google Scholar 

  13. Lei Y, Yung KL, Xu Y (2010) Chaos synchronization and parameter estimation of single-degree-of-freedom oscillators via adaptive control. J Sound Vib 329(8):973–979

    Article  Google Scholar 

  14. Zhang Z, Wang Y, Du Z (2012) Adaptive synchronization of single-degree-of-freedom oscillators with unknown parameters. Appl Math Comput 218(12):6833–6840

    MathSciNet  MATH  Google Scholar 

  15. Yan JJ, Hung ML, Liao TL (2006) Adaptive sliding mode control for synchronization of chaotic gyros with fully unknown parameters. J Sound Vib 298(1–2):298–306

    Article  MathSciNet  Google Scholar 

  16. Yuan J, Shi B, Xiu G (2016) Sliding control for single-degree-of-freedom fractional oscillators. arXiv preprint arXiv:1608.04850

  17. Haibo Du, Xinghuo Yu, Michael Z.Q. Chen, Shihua Li, (2016) Chattering-free discrete-time sliding mode control. Automatica 68:87-91

    Article  MathSciNet  Google Scholar 

  18. Du HB, Wen GH, Cheng YY, He YG, Jia RT (2017) Distributed finite-time cooperative control of multiple high-order nonholonomic mobile robots. IEEE Trans Neural Netw Learn Syst 28(12):2998–3006

    Article  MathSciNet  Google Scholar 

  19. Du HB, Wen GH, Yu XH, Li SH, Chen MZQ (2015) Finite-time consensus of multiple nonholonomic chained-form systems based on recursive distributed observer. Automatica 62(12):236–242

    Article  MathSciNet  Google Scholar 

  20. Du HB, He YG, Cheng YY (2014) Finite-time synchronization of a class of second-order nonlinear multi-agent systems using output feedback control. IEEE Trans Circuits Syst I Regul Pap 61(6):1778–1788

    Article  Google Scholar 

  21. Sun H, Hou L, Zong G (2016) Continuous finite time control for static var compensator with mismatched disturbances. Nonlinear Dyn 85(4):2159–2169

    Article  Google Scholar 

  22. Aghababa MP, Khanmohammadi S, Alizadeh G (2011) Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique. Appl Math Model 35(6):3080–3091

    Article  MathSciNet  Google Scholar 

  23. Li S, Tian YP (2003) Finite time synchronization of chaotic systems. Chaos Solitons Fractals 15(2):303–310

    Article  MathSciNet  Google Scholar 

  24. Filippov AF (1988) Differential equations with discontinuous right-hand sides. Kluwer Academic, New York

    Book  Google Scholar 

  25. Polyakov A (2012) Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans Autom Control 57(8):2106–2110

    Article  MathSciNet  Google Scholar 

  26. Zuo ZY (2015) Non-singular fixed-time terminal sliding mode control of non-linear systems. IET Control Theory Appl 9(4):545–552

    Article  MathSciNet  Google Scholar 

  27. Ni JK, Liu L, Liu CX, Hu XY, Li SL (2017) Fast fixed-time nonsingular terminal sliding mode control and its application to chaos suppression in power system. IEEE Trans Circuits Syst II Express Briefs 64(2):151–155

    Article  Google Scholar 

  28. Park J, Sandberg IW (1991) Universal approximation using radial-basis-function networks. Neural Comput 3(2):246–257

    Article  Google Scholar 

  29. Sanner RM, Slotine JJ (1992) Gaussian networks for direct adaptive control. IEEE Trans Neural Netw 3(6):837–863

    Article  Google Scholar 

  30. Sun H, Guo L (2017) Neural network-based DOBC for a class of nonlinear systems with unmatched disturbances. IEEE Trans Neural Netw Learn Syst 28(2):482–489

    Article  MathSciNet  Google Scholar 

  31. Li CJ, Yu XH, Huang TW, Chen G, He X (2016) A generalized Hopfield network for nonsmooth constrained convex optimization: Lie derivative approach. IEEE Trans Neural Netw Learn Syst 27(2):308–321

    Article  MathSciNet  Google Scholar 

  32. Bhat SP, Bernstein DS (1995) Lyapunov analysis of finite-time differential equations. In: Proceedings of the American control conference, 1831–1832

  33. Bhat SP, Bernstein DS (1998) Continuous finite-time stabilization of the translational and rotational double integrators. IEEE Trans Autom Control 43(5):678–682

    Article  MathSciNet  Google Scholar 

  34. Feng Y, Yu X, Man Z (2002) Non-singular terminal sliding mode control of rigid manipulators. Automatica 28(11):2159–2167

    Article  MathSciNet  Google Scholar 

  35. Sun HB, Li SH, Sun CY (2013) Finite time integral sliding mode control of hypersonic vehicles. Nonlinear Dyn 73(1–2):229–244

    Article  MathSciNet  Google Scholar 

  36. Li YK, Sun HB, Zong GD, Hou LL (2017) Composite anti-disturbance resilient control for Markovian jump nonlinear systems with partly unknown transition probabilities and multiple disturbances. Int J Robust Nonlinear Control 27(14):2323–2337

    Article  MathSciNet  Google Scholar 

  37. Xu B, Sun FC (2018) Composite intelligent learning control of strict feedback systems with disturbance. IEEE Trans Cybern 48(2):730–741

    Article  Google Scholar 

  38. Sun HB, Li YK, Zong GD, Hou LL (2018) Disturbance attenuation and rejection for stochastic Markovian jump system with partially known transition probabilities. Automatica 89:349–357

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National natural Science Foundation of China (Nos. 61773236, 61773235), and the Postdoctoral Science Foundation of China (2017M612236, 2017M611222).

Author information

Authors and Affiliations

  1. School of Engineering, Qufu Normal University, Rizhao, P. R. China

    Haibin Sun

  2. School of Information Science and Engineering, Qufu Normal University, Rizhao, P. R. China

    Linlin Hou

  3. School of Engineering, RMIT University, Melbourne, Australia

    Chaojie Li

Authors
  1. Haibin Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Linlin Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chaojie Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chaojie Li.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interests.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, H., Hou, L. & Li, C. Synchronization of single-degree-of-freedom oscillators via neural network based on fixed-time terminal sliding mode control scheme. Neural Comput & Applic 31, 6365–6372 (2019). https://doi.org/10.1007/s00521-018-3445-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-018-3445-x

Keywords

Search

Navigation