Abstract
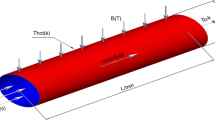
The present study analyzes the heat transfer in the flow of copper–water nanofluids between parallel plates. For effective thermal conductivity of nanofluids, Hamilton and Crosser's model has been utilized to examine the flow by considering different shape factors. By employing the suitable similarity transformations, the equations governing the flow are transformed into a set of nonlinear ordinary differential equations. The resulting set of equations is solved numerically with the help of Runge–Kutta–Fehlberg numerical scheme. The graphical simulation presents the analysis of variations, in velocity and temperature profiles, for emerging parameters. A comprehensive discussion also accompanies the graphical results. Moreover, the effects of relevant parameters, on skin friction coefficient and Nusselt number, are highlighted graphically. It is noticed that the velocity field is an increasing function of all the parameters involved. Furthermore, the temperature of the fluid is maximum for the platelet-shaped particles followed by the cylinder- and brick-shaped particles.











Similar content being viewed by others
Abbreviations
- \(\check{u}\) :
-
Component of velocity in x direction
- \(\check{v}\) :
-
Component of velocity in y direction
- \(\check{T}\) :
-
Temperature of the fluid
- p :
-
Pressure
- \({\rho_{\text{nf}}}\) :
-
Density of nanofluid
- \({\mu_{\text{nf}}}\) :
-
Viscosity of the fluid
- \({\alpha_{\text{nf}}}\) :
-
Thermal diffusivity of the fluid
- \({\sigma_{\text{nf}}}\) :
-
Electrical conductivity of the nanofluid
- \({k_{\text{f}}}\) :
-
Conductivity of the base fluid
- \({k_{\text{s}}}\) :
-
Conductivity of the nanoparticles
- \(\theta\) :
-
Dimensionless temperature
- \(\phi\) :
-
Volume fraction of nanoparticles
- \(m\) :
-
Shape factor of nanoparticles
- \({\rho_{\text{f}}}\) :
-
Density of base fluid
- \({\rho_{\text{s}}}\) :
-
Density of nanoparticles
- \({\left( {\rho {C_{\text{p}}}} \right)_{\text{f}}}\) :
-
Heat capacity of base fluid
- \({\left( {\rho {C_{\text{p}}}} \right)_{\text{s}}}\) :
-
Heat capacity of nanoparticles
- \({\sigma_{\text{s}}}\) :
-
Electrical conductivity of the base fluid
- \({\sigma_{\text{f}}}\) :
-
Electrical conductivity of the nanoparticles
- \(\eta\) :
-
Dimensionless variable
- \(F\) :
-
Dimensionless velocity along the x direction
- \(F^{\prime}\) :
-
Dimensionless velocity along the y direction
- \(\varTheta\) :
-
Dimensionless temperature
- \({C_{\text{f}}}\) :
-
Skin friction coefficient
- \(Nu\) :
-
Nusselt number
References
Choi SUS (1995) Enhancing thermal conductivity of fluids with nanoparticle. In: Siginer DA, Wang HP (eds) Developments and applications of non-newtonian flows, ASME FED, vol 231/MD 66, pp 99–105
Choi SUS, Zhang ZG, Yu W, Lockwood FE, Grulke EA (2001) Anomalously thermal conductivity enhancement in nanotube suspensions. Appl Phys Lett 79:2252–2254
Buongiorno J (2006) Convective transport in nanofluids. ASME J Heat Transf 128:240–250
Timofeeva Elena V, Routbort JL, Singh D (2009) Particle shape effects on thermophysical properties of alumina nanofluids. J Appl Phys 106(1):014304–014310
Murshed SMS, Nieto de Castro CA, Lourenço MJV, Lopes MLM, Santos FJV (2011) A review of boiling and convective heat transfer with nanofluids. Renew Sustain Energy Rev 15(5):2342–2354
Khan W, Pop I (2010) Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transf 53(11):2477–2483
Sheikholeslami M, Ellahi R, Hassan M, Soleimani S (2014) A study of natural convection heat transfer in a nanofluid filled enclosure with elliptic inner cylinder. Int J Numer Methods Heat Fluid Flow 24(8):1906–1927
Nawaz M, Zeeshan A, Ellahi R, Abbasbandy S, Rashidi S (2015) Joules heating effects on stagnation point flow over a stretching cylinder by means of genetic algorithm and Nelder–Mead method. Int J Numer Methods Heat Fluid Flow 25(3):665–684
Mohyud-Din ST, Khan U, Ahmed N, Hassan SM (2015) Magnetohydrodynamic flow and heat transfer of nanofluids in stretchable convergent/divergent channels. Appl Sci 5:1639–1664
UlHaq R, Nadeem S, Khan ZH, Noor NFM (2015) Convective heat transfer in MHD slip flow over a stretching surface in the presence of carbon nanotubes. Phys B 457:40–47
Mohyud-Din ST, Ahmed N, Khan U, Waheed A, Hussain S, Darus M (2016) On combined effects of heat transfer and chemical reaction for the flow through asymmetric channel with orthogonally deformable porous walls. Math Probl Eng. Article ID 2568785. doi:10.1155/2016/2568785
Mabood F, Khan WA, Ismail AIM (2015) MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: a numerical study. J Magn Magn Mater 374:569–576
Khan U, Mohyud-Din ST, Mohsin BB (2016) Convective heat transfer and thermo-diffusion effects on flow of nanofluid towards a permeable stretching sheet saturated by a porous medium. Aerosp Sci Technol 50:196–203
Mohyud-Din ST, Zaidi ZA, Khan U, Ahmed N (2015) On heat and mass transfer analysis for the flow of a nanofluid between rotating parallel plates. Aerosp Sci Technol 46:514–522
Khan U, Ahmed N, Mohyud-Din ST (2015) Heat transfer effects on carbon nanotubes suspended nanofluid flow in a channel with non-parallel walls under the effect of velocity slip boundary condition: a numerical study. Neural Comput Appl. doi:10.1007/s00521-015-2035-4 (Accepted)
Noor NFM, Haq Rizwan Ul, Nadeem S, Hashim I (2015) Mixed convection stagnation flow of a micropolar nanofluid along a vertically stretching surface with slip effects. Meccanica. doi:10.1007/s11012-015-0145-9
Kandelousi MS (2014) Effect of spatially variable magnetic field on ferrofluid flow and heat transfer considering constant heat flux boundary condition. Eur Phys J Plus 129:248
Kandelousi MS (2014) KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel. Phys Lett A 378(45):3331–3339
Sheikholeslami M (2015) Effect of uniform suction on nanofluid flow and heat transfer over a cylinder. J Braz Soc Mech Sci Eng 37:1623–1633
Sheikholeslami M, Ganji DD, Rashidi MM (2016) Magnetic field effect on unsteady nanofluid flow and heat transfer using Buongiorno model. J Magn Magn Mater 16:164–173
Sheikholeslami M, Chamkha AJ (2016) Flow and convective heat transfer of a ferro-nanofluid in a double-sided lid-driven cavity with a wavy wall in the presence of a variable magnetic field. Numer Heat Transfer Part A 69(10):1186–1200
Sheikholeslami M, Rashidi MM, Hayatd T, Ganji DD (2016) Free convection of magnetic nanofluid considering MFD viscosity effect. J Mol Liq 218:393–399
Sheikholeslami M, Hayat T, Alsaedi A (2016) MHD free convection of Al2O3–water nanofluid considering thermal radiation: a numerical study. Int J Heat Mass Transf 96:513–524
Sheikholeslami M, Rashidi MM (2016) Non-uniform magnetic field effect on nanofluid hydrothermal treatment considering Brownian motion and thermophoresis effects. J Braz Soc Mech Sci Eng 38:1171–1184
Sheikholeslami M, Vajravelu K, Rashidi MM (2016) Forced convection heat transfer in a semi annulus under the influence of a variable magnetic field. Int J Heat Mass Transf 92:339–348
Sheikholeslami M, Rashidi MM, Ganji DD (2015) Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4–water nanofluid. Comput Methods Appl Mech Eng 294:299–312
Sheikholeslami M, Ganji DD (2014) Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer. Energy 75:400–410
Ul R (2016) Haq, N.F.M. Noor, Z.H. Khan, Numerical simulation of water based magnetite nanoparticles between two parallel disks, 2016. Adv Powder Technol 27(4):1568–1575
Ul Haq R, Nadeem S, Khan ZH, Noor NFM (2015) MHD squeezed flow of water functionalized metallic nanoparticles over a sensor surface. Phys E 73:45–53
Hatami M, Ganji DD (2014) Heat transfer and nanofluid flow in suction and blowing process between parallel disks in presence of variable magnetic field. J Mol Liq 190:159–168
Sheikholeslami M, Ganji DD (2013) Heat transfer of Cu–water nanofluid flow between parallel plates. Powder Technol 235:873–879
Sheikholeslami M, Hatami M, Ganji DD (2014) Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J Mol Liq 190:112–120
Mahmoodi M, Kandelousi S (2015) Analysis of the hydrothermal behavior and entropy generation in a regenerative cooling channel considering thermal radiation. Nucl Eng Des 291:277–286
Hamilton RL, Crosser OK (1962) Thermal conductivity of heterogeneous two-component systems. Ind Eng Chem Fundam 1(3):187–191
Ellahi R, Hassan M, Zeeshan A (2015) Shape effects of nanosize particles in Cu–H2O nanofluid on entropy generation. Int J Heat Mass Transf 81:449–456
Sher Akber N, Butt AW (2015) Ferromagnetic effects for peristaltic flow of Cu–water nanofluid for different shapes of nanosize particles. Appl Nanosci. doi:10.1007/s13204-015-0430-x
Ellahi R, Hassan M, Zeeshan A, Khan AA, The shape effects of nanoparticles suspended in HFE-7100 over wedge with entropy generation and mixed convection. Appl Nanosci. doi:10.1007/s13204-015-0481-z
Sheikholeslami M, Rashidi MM, Al Saad DM, Firouzi F, Rokni HB, Domairry G, Steady nanofluid flow between parallel plates considering thermophoresis and Brownian effects. J King Saud Univ Sci. doi:10.1016/j.jksus.2015.06.003
Mahmoodi M, Kandelousi S (2015) Application of DTM for kerosene-alumina nanofluid flow and heat transfer between two rotating plates. Eur Phys J Plus 130:142
Sheikholeslami M, Ganji DD (2014) Three dimensional heat and mass transfer in a rotating system using nanofluid. Powder Technol 253:789–796
Noor NFM, Kechil SA, Hashim I (2010) Simple non-perturbative solution for MHD viscous flow due to a shrinking sheet. Commun Nonlinear Sci Numer Simul 15(2):144–148
Nadeem S, Haq RU, Lee C (2012) MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci Iran 19:1150–1553
Khan U, Ahmed N, Khan SIU, Bano S, Mohyud-din ST (2014) Unsteady squeezing flow of Casson fluid between parallel plates. World J Model Simul 10(4):308–319
Ebaid A (2008) A new numerical solution for the MHD peristaltic flow of a bio-fluid with variable viscosity in a circular cylindrical tube via Adomian decomposition method. Phys Lett A 372:5321–5328
Ebaid A (2011) A new analytical and numerical treatment for singular two-point boundary value problems via the Adomian decomposition method. J Comput Appl Math 235:1914–1924
Ebaid A (2011) Approximate analytical solution of a nonlinear boundary value problem and its application in fluid mechanics. Zeitschrift für Naturforschung A 66:423–426
Aly EH, Ebaid A, Rach R (2012) Advances in the Adomian decomposition method for solving two-point nonlinear boundary value problems with Neumann boundary conditions. Comput Math Appl 63:1056–1065
Chun C, Ebaid A, Lee M, Aly E (2012) An approach for solving singular two point boundary value problems: analytical and numerical treatment. Aust N Z Ind Appl Math J 53E:21–43
Ebaida A, Aljoufi MD, Wazwaz AM (2015) An advanced study on the solution of nanofluid flow problems via Adomian’s method. Appl Math Lett 46:117–122
Mohyud-Din ST, Noor MA, Waheed A (2010) Variation of parameter method for initial and boundary value problems. World Appl Sci J 11:622–639
Khan U, Ahmed N, Zaidi ZA, Jan SU, Mohyud-Din ST (2013) On Jeffery-Hamel Flows. Int J Mod Math Sci 7:236–247
Mohyud-Din ST, Noor MA, Waheed A (2009) Variation of parameter method for solving sixth-order boundary value problems. Commun Korean Math Soc 24:605–615
Khan U, Ahmed N, Sikander W, Mohyud-Din ST (2015) A study of Velocity and temperature slip effects on flow of water based nanofluids in converging and diverging channels. Int J Appl Comput Math 1(4):569–587
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors of this manuscript declare that there is no conflict of interest regarding the publication of this manuscript.
Rights and permissions
About this article
Cite this article
Khan, U., Ahmed, N. & Mohyud-Din, S.T. Analysis of magnetohydrodynamic flow and heat transfer of Cu–water nanofluid between parallel plates for different shapes of nanoparticles. Neural Comput & Applic 29, 695–703 (2018). https://doi.org/10.1007/s00521-016-2596-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-016-2596-x