Estimation of nearshore wave transmission for submerged breakwaters using a data-driven predictive model

Abstract

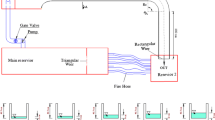
The functional design of submerged breakwaters is still developing, particularly with respect to modelling of the nearshore wave field behind the structure. This paper describes a method for predicting the wave transmission coefficients behind submerged breakwaters using machine learning algorithms. An artificial neural network using the radial-basis function approach has been designed and trained using laboratory experimental data expressed in terms of non-dimensional parameters. A wave transmission coefficient calculator is presented, based on the proposed radial-basis function model. Predictions obtained by the radial-basis function model were verified by experimental measurements for a two dimensional breakwater. Comparisons reveal good agreement with the experimental results and encouraging performance from the proposed model. Applying the proposed neural network model for predictions, guidance is given to appropriately calculate wave transmission coefficient behind two dimensional submerged breakwaters. It is concluded that the proposed predictive model offers potential as a design tool to predict wave transmission coefficients behind submerged breakwaters. A step-by-step procedure for practical applications is outlined in a user-friendly form with the intention of providing a simplified tool for preliminary design purposes. Results demonstrate the model’s potential to be extended to three dimensional, rough, permeable structures.

Appendices

Appendix 1: A simplified tool and initial prediction scheme with a step by step procedure (K _t calculator)

The algorithm used in this appendix is based closely on the algorithm introduced by [12] and the later work by Sharif Ahmadian [36].

As explained in Sect. 5, the final optimized RBF network has one radial basis function layer with 15 nodes. A K _t calculator including details about the model mathematics is described below, based on the proposed non-dimensional RBF model. A step-by-step procedure for practical applications is outlined in a user-friendly form [12, 36] with the intention of providing an initial prediction scheme according to the proposed ANN model described in the paper. For more details and theoretical aspects see [63] or [64].

Referring first to the non-dimensional parameters used throughout the paper, an input vector I should be considered:

$$I = \left[ {\xi_{o} ,H_{i} /h,h_{s} /H_{i} ,B/H_{i} } \right].$$

(20)

The normalization process according to the Eq. (7) is performed:

$$I_{n} = {{\left( {I - I_{\hbox{min} } } \right)} \mathord{\left/ {\vphantom {{\left( {I - I_{\hbox{min} } } \right)} {\left( {I_{\hbox{max} } - I_{\hbox{min} } } \right)}}} \right. \kern-0pt} {\left( {I_{\hbox{max} } - I_{\hbox{min} } } \right)}}$$

(21)

where vectors I _min, I _max are characterized by values:

$$I_{\hbox{min} } = \left[ {3.7066,0.0348,0.0000,1.8775} \right]$$

(22)

$$I_{\hbox{max} } = \left[ {15.4525,0.5384,10.7259,51.5480} \right].$$

(23)

Considering the center and weight matrices defined below, the input signals are passed through the network. The center matrix c and weight vector w are applied in the transfer functions Eqs. (26) and (30) respectively. The values in the last column of the center matrix c and the weight vector w are the bias values for the hidden and output layers respectively.

$$c = \left( {\begin{array}{*{20}l} {0.8994} \hfill & {0.0000} \hfill & {1.0000} \hfill & {0.3382} \hfill & {0.8326} \hfill \\ {0.6765} \hfill & {0.0093} \hfill & {0.2950} \hfill & {0.8542} \hfill & {0.8326} \hfill \\ {0.6631} \hfill & {0.0115} \hfill & {0.5742} \hfill & {0.7062} \hfill & {0.8326} \hfill \\ {0.5942} \hfill & {0.0086} \hfill & {0.2979} \hfill & {0.8629} \hfill & {0.8326} \hfill \\ {0.4123} \hfill & {0.0193} \hfill & {0.7819} \hfill & {0.2562} \hfill & {0.8326} \hfill \\ {0.4341} \hfill & {0.0269} \hfill & {0.2410} \hfill & {0.5867} \hfill & {0.8326} \hfill \\ {0.4268} \hfill & {0.0288} \hfill & {0.4728} \hfill & {0.4726} \hfill & {0.8326} \hfill \\ {0.7090} \hfill & {0.0868} \hfill & {0.0000} \hfill & {0.2296} \hfill & {0.8326} \hfill \\ {1.0000} \hfill & {0.0433} \hfill & {0.4084} \hfill & {0.2396} \hfill & {0.8326} \hfill \\ {0.5901} \hfill & {0.0093} \hfill & {0.2952} \hfill & {0.9821} \hfill & {0.8326} \hfill \\ {0.2849} \hfill & {0.0608} \hfill & {0.5321} \hfill & {0.1623} \hfill & {0.8326} \hfill \\ {0.3095 \, } \hfill & {0.0954} \hfill & {0.1406} \hfill & {0.1444} \hfill & {0.8326} \hfill \\ {0.4292} \hfill & {0.0977} \hfill & {0.1350} \hfill & {0.1727} \hfill & {0.8326} \hfill \\ {0.6522} \hfill & {0.0133} \hfill & {0.5615} \hfill & {0.9322} \hfill & {0.8326} \hfill \\ {0.3449} \hfill & {0.1031} \hfill & {0.0000} \hfill & {0.2043} \hfill & {0.8326} \hfill \\ \end{array} } \right)$$

(24)

$$w = \left\{ {35.2393\quad - 186.0468\quad - 179.6246\quad 733.9377\quad - 66.3753\quad - 180.8649\quad 57.2453\quad - 2.2679\quad - 2.3436\quad - 379.9198\quad 85.0211\quad - 76.2526\quad 39.5692\quad 93.4942\quad 29.6973} \right\}$$

(25)

Activation functions of radial basis type are used to determine the values of hidden neurons, such as:

$$a_{1} (i,1) = \exp ( - ({\text{dist}}(c(i,:),a_{o} ) \cdot d)^{2} );\quad {\text{for}}\;i:1 \ldots 15$$

(26)

where

$$a_{o} (5,1) = 1$$

(27)

and constant value d is:

$$d = {\text{sqrt}}( - \log (.5))/{\text{sp}}$$

(28)

where sp = 1.0.

The Euclidean distance between the vectors a _o and c, is defined as follows:

$${\text{dist}}(c_{i} - a_{o,i} ) = \sqrt {\left( {\sum {\left( {c_{i} - a_{o,i} } \right)^{2} } } \right)} \quad {\text{for}}\;i:1 \ldots 5$$

(29)

where c _i and a _o,i are the coordinates of c and a _o,i in dimension i.

Whereas a linear activation function has been applied, the scaled model outcome can be computed as follows:

$$a_{2} = w \cdot a_{1} + b_{2}$$

(30)

where b ₂ =  0.3438 is the bias neuron for the output layer.

Finally, the model output needs to be rescaled. Thus, K _t is calculated as follows:

$$K_{t} = \left( {O_{\hbox{max} } - O_{\hbox{min} } } \right) \cdot *a_{2} + O_{\hbox{min} }$$

(31)

where O _min = 0.1187 and O _max = 0.8416.

The main aim is to introduce a simplified tool for preliminary design purposes which can be used in submerged breakwater design. Although the model is calibrated and designed using regular wave data, similar predictions can be made using significant wave height (H _s )/zero moment wave height (H _mo) and peak wave period, T _p as inputs. However, some considerations might be required in applying regular wave results to random sea‐states [12, 36].

Appendix 2: Radial basis function (RBF) network

This appendix gives a concise description of the training algorithm adopted in this paper for the RBF network.

In engineering applications, the most popular artificial neural network is the multi-layer perceptron (MLP). Radial basis function (RBF) networks with universal non-linear approximation properties are similar to the multi-layer perceptron in that they also use memory-based learning algorithms for their design [63, 71].

RBF networks are used widely for non-linear function approximation comparable to MLP networks [72, 73], with some additional benefits, for instance, RBFs are trained usually with a relatively higher speed [74]. The concept of a RBF neural network was introduced by Broomhead and Lowe [72]. In the same way as for a MLP network, the entire data set is split into two main data sets and training and testing performed in two distinct stages [72, 73].

While the number of layers in MLP can be variable, RBF networks are always designed with three layers of neurons: input layer, hidden layer and output layer. Working as a feed-forward RBF network: the input layer receives the input data, the hidden layer computes the outcome of the RBF units and the output layer combines the outputs from the RBF units linearly. The input and output layers in a RBF network are thus the same as in MLP, while the hidden layer is not. The main difference is related to the transfer functions applied in the hidden layer. The Euclidean distance between the input vector and the RBF unit’s centre vector c is calculated in the RBF networks while an MLP unit applies a transfer function which computes the inner product of the weight and the input vectors [63].

RBF models include biases in their hidden and output layers similar to MLP. However, RBF models usually have more computational units in the hidden layer than MLP as their transfer functions respond to a smaller area of the input space than MLP. This is of benefit as it requires less training time to design RBF compared with MLP. The outputs are also weighted. Hence, an expression of the RBF network can be presented as [75]:

$$y(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} ) = \sum\limits_{k = 1}^{n} {w_{k} \phi \left( {\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} - c_{k} } \right\|} \right) + b}$$

(32)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$ is the input vector, $w_{1} ,w_{2} , \ldots w_{n}$ are weight factors, c _k represents the centre of the kth RBF unit, b is bias value and Φ is the hidden layer transfer function (Gaussian function):

$$\phi \left( {\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} - c_{k} } \right\|} \right) = e^{{ - \left( {{{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} - c_{k} } \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} - c_{k} } \right\|^{2} } {2s_{k}^{2} }}} \right. \kern-0pt} {2s_{k}^{2} }}} \right)}}$$

(33)

where s _k is the scaling factor of the kth RBF unit [75].

Basically, the learning process in RBF networks is a form of supervised learning. Determining and making an appropriate decision on the number of computational neurons is basically an essential step since it influences the network complexity and its generalizing capability. Insufficient computational units mean the RBF network may not estimate the underlying function adequately. However, increasing the size of hidden layer (number of the computational neurons) may cause an overlearning situation [76]. In addition, carefully specifying the optimal locations of the centres and scaling factors in the computational neurons of the hidden layer would be important tasks over the training process and very essential to obtain proper results. The most preferred form of transfer functions for a computational neuron is the Gaussian function [75, 77, 78].

The next step is for the weights of the network to be computed. At last, the bias values added to each output are calculated. A derivative-based gradient descent algorithm [78] is used in this study, chosen from the various algorithms proposed in the literature for training RBF networks.

Following the training procedure and having decided on the number of hidden units, c, s, w and b parameters are determined. The sum of squared errors (SSE) is typically applied over the training process to check the manner of functioning of the RBF network and is defined as follows [79]:

$$E(c,s,w,b) = \sum\limits_{j = 1}^{J} {(y_{j} - \hat{y}_{j} )^{2} }$$

(34)

where y and $\hat{y}$ are the actual and desired outputs respectively.

The training procedure for a RBF network is organised using the following procedure [63]. The hidden layer initially has zero number of units. Data samples are presented to the network, signals pass through the network and the error is computed. The calculated output is compared to the target value of the respective sample. An RBF unit is added. The process is performed repeatedly and the connection weight parameters are then computed to meet the desired error. Basically, the calculated error, which is statistically described as the sum of squared errors (SSE), must be lower than the desired error. In addition, the maximum number of hidden neurons should be met before stopping training [63].

In the present case in this study, a 15-node hidden layer network was chosen. The training of the RBF model was terminated once the calculated error reached the desired values (in this study 0.01) or the chosen number of training iterations (here 100) had been completed.