Abstract
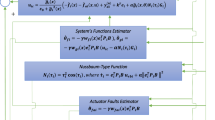
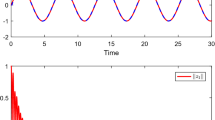
In this paper, a delay replacement-based adaptive fault-tolerant control method is proposed for a double inverted pendulum connected by an unknown device. By combining fuzzy approximation and integer backstepping, a new time-delay assumption-independent state feedback decentralized control scheme is developed based on directly replacing the unbounded time-delay argument of fuzzy approximators with the bounded reference signals. Furthermore, all of the two typical types of actuator faults can be compensated for on-line. Compared with the existing results, the time-delay assumptions that need to be test and verify in applications are eliminated, and global bounded stability of the closed-loop system is guaranteed. Simulation results are provided to show the effectiveness of the control approach.










Similar content being viewed by others
References
Yi J, Yubazaki N, Hirota K (2002) A new fuzzy controller for stabilization of parallel-type double inverted pendulum system. Fuzzy Sets Syst 126(1):105–119
Spooner JT, Passino KM (1999) Decentralized adaptive control of nonlinear systems using radial basis neural networks. IEEE Trans Autom Control 44(11):2050–2057
Chen WS, Li JM (2008) Decentralized output-feedback neural control for systems with unknown interconnections. IEEE Trans Syst Man Cybern Part B-Cybern 38(1):258–266
Nguang SK (2000) Robust stabilization of a class of time-delay nonlinear systems. IEEE Trans Autom Control 45(4):756–762
Fu YS, Tian ZH, Shi SJ (2003) State feedback stabilization for a class of stochastic time-delay nonlinear systems. IEEE Trans Autom Control 48(2):282–286
Guo T, Liu GY (2011) Adaptive fuzzy control for unknown nonlinear time-delay systems with virtual control functions. Int J Control Autom Syst 9(6):1227–1234
Zhou Q, Shi P, Xu SY, Li HY (2013) Adaptive output feedback control for nonlinear time-delay systems by fuzzy approximation approach. IEEE Trans Fuzzy Syst 21(2):301–313
Wu J, Chen WS, Li J (2015) Fuzzy-approximation-based global adaptive control for uncertain strict-feedback systems with a priori known tracking accuracy. Fuzzy Sets Syst 273:1–25
Yoo SJ, Park JB (2012) Decentralized adaptive output-feedback control for a class of nonlinear large-scale systems with unknown time-varying delayed interactions. Inf Sci 186(1):222–238
Guo T, Wang AM (2012) Simplified output feedback stabilization for time-delay interconnected systems based on dynamic surface control. Int Rev Comput Softw 7(1):275–282
Yang Y, Yue D, Xue YS (2015) Decentralized adaptive neural output feedback control of a class of large-scale time-delay systems with input saturation. J Frankl Inst-Eng Appl Math 352(5):2129–2151
Zhou Q, Shi P, Xu SY, Li HY (2013) Observer-based adaptive neural network control for nonlinear stochastic systems with time delay. IEEE Trans Neural Netw Learn Syst 24(1):71–80
Chen B, Liu XP, Liu KF, Lin C (2013) Adaptive fuzzy tracking control of nonlinear MIMO systems with time-varying delays. Fuzzy Sets Syst 217:1–21
Chen B, Liu XP, Liu KF, Lin C (2013) Adaptive control for nonlinear MIMO time-delay systems based on fuzzy approximation. Inf Sci 222:576–592
Zhang X, Lin Y (2015) Adaptive control of nonlinear time-delay systems with application to a two-stage chemical reactor. IEEE Trans Autom Control 60(4):1074–1079
Ge SS, Hong F, Lee TH (2004) Adaptive neural control of nonlinear time-delay systems with unknown virtual control coefficients. IEEE Trans Syst Man Cyberns, Part B (Cybern) 34(1):499–516
Ge SS, Hong F, Lee TH (2005) Robust adaptive control of nonlinear systems with unknown time delays. Automatica 41(7):1181–1190
Chen B, Liu XP, Liu KF, Shi P, Lin C (2010) Direct adaptive fuzzy control for nonlinear systems with time-varying delays. Inf Sci 180(5):776–792
Tong SC, Li Y, Li YM, Liu YJ (2011) Observer-based adaptive fuzzy backstepping control for a class of stochastic nonlinear strict-feedback systems. IEEE Trans Syst Man Cybern, Part B (Cybern) 41(6):1693–1704
Choi JY, Farrell JA (2001) Adaptive observer backstepping control using neural networks. IEEE Trans Neural Netw 12(5):1103–1112
Wang C, Hill DJ, Ge SS, Chen GR (2006) An ISS-modular approach for adaptive neural control of pure-feedback systems. Automatica 42(5):723–731
Chen WS, Zhang ZQ (2010) Globally stable adaptive backstepping fuzzy control for output-feedback systems with unknown high-frequency gain sign. Fuzzy Sets Syst 161(6):821–836
Chen WS, Jiao LC, Wu JS (2012) Globally stable adaptive robust tracking control using RBF neural networks as feedforward compensators. Neural Comput Appl 21(2):351–363
Huang JT (2012) Global tracking control of strict-feedback systems using neural networks. IEEE Trans Neural Netw Learn Syst 23(11):1714–1725
Wu J, Chen WS, Yang FZ, Li J, Zhu Q (2015) Global adaptive neural control for strict-feedback time-delay systems with predefined output accuracy. Inf Sci 301:27–43
Wang ML, Zhang ZQ (2015) Globally adaptive asymptotic tracking control of nonlinear systems using nonlinearly parameterized fuzzy approximator. J Frankl Inst-Eng Appl Math 352(7):2783–2795
Wu J, Chen WS, Zhao D, Li J (2013) Globally stable direct adaptive backstepping NN control for uncertain nonlinear strict-feedback systems. Neurocomputing 122:134–147
Wu J, Li J, Chen WS (2014) Semi-globally/globally stable adaptive NN backstepping control for uncertain MIMO systems with tracking accuracy known a priori. J Frankl Inst-Eng Appl Math 351(12):5274–5309
Huang JT (2015) Global adaptive neural dynamic surface control of strict-feedback systems. Neurocomputing 165:403–413
Fu J, Ma RC, Chai TY (2015) Global finite-time stabilization of a class of switched nonlinear systems with the powers of positive odd rational numbers. Automatica 54:360–373
Xu B, Yang CG, Pan YP (2015) Global neural dynamic surface tracking control of strict-feedback systems with application to hypersonic flight vehicle. IEEE Trans Neural Netw Learn Syst 26(10):2563–2575
Chen WS, Ge SS, Wu J, Gong MG (2015) Globally stable adaptive backstepping neural network control for uncertain strict-feedback systems with tracking accuracy known a priori. IEEE Trans Neural Netw Learn Syst 26(9):1842–1854
Tang XD, Tao G, Joshi SM (2003) Adaptive actuator failure compensation for parametric strict feedback systems and an aircraft application. Automatica 39(11):1975–1982
Li P, Yang GH (2009) Backstepping adaptive fuzzy control of uncertain nonlinear systems against actuator faults. J Control Theory Appl 7(3):248–256
Meng LY, Jiang B (2009) Backstepping-based active fault-tolerant control for a class of uncertain SISO nonlinear systems. J Syst Eng Electron 20(6):1263–1270
Wang W, Wen CY (2010) Adaptive actuator failure compensation control of uncertain nonlinear systems with guaranteed transient performance. Automatica 46(12):2082–2091
Fan HJ, Liu B, Shen YD, Wang W (2014) Adaptive failure compensation control for uncertain systems with stochastic actuator failures. IEEE Trans Autom Control 59(3):808–814
Fan HJ, Liu B, Wang W, Wen CY (2015) Adaptive fault-tolerant stabilization for nonlinear systems with Markovian jumping actuator failures and stochastic noises. Automatica 51:200–209
Zhang ZQ, Xu SY, Guo Y, Chu YM (2010) Robust adaptive output-feedback control for a class of nonlinear systems with time-varying actuator faults. Int J Adapt Control Signal Process 24(9):743–759
Tong SC, Huo BY, Li YM (2014) Observer-based adaptive decentralized fuzzy fault-tolerant control of nonlinear large-scale systems with actuator failures. IEEE Trans Fuzzy Syst 22(1):1–15
Xu YY, Tong SC, Li YM (2015) Adaptive fuzzy decentralised fault-tolerant control for nonlinear large-scale systems with actuator failures and unmodelled dynamics. Int J Syst Sci 46(12):2195–2209
Krstic M, Kokotovic PV, Kanellakopoulos I (1995) Nonlinear and adaptive control design. Wiley, New York
Boskovic JD, Mehra RK, Stable multiple model adaptive flight control for accommodation of a large class of control effector failures. In: Proceedings of the 1999 American control conference. IEEE, 2–4 June 1999, vol 3, pp 1920–1924
Wang LX (1994) Adaptive fuzzy systems and control: design and stability analysis. Prentice-Hall, Englewood Cliffs
Wang LX (1995) Design and analysis of fuzzy identifiers of nonlinear dynamic systems. IEEE Trans Autom Control 40(1):11–23
Tang XD, Tao G, Joshi SM (2007) Adaptive actuator failure compensation for nonlinear MIMO systems with an aircraft control application. Automatica 43(11):1869–1883
Polycarpou MM (1996) Stable adaptive neural control scheme for nonlinear systems. IEEE Trans Autom Control 41(3):447–451
Acknowledgments
This work was supported by the Innovation Scientists and Technicians Troop Construction Projects of Henan Province (C20150028), the Program for Science & Technology Innovation Talents in Universities of Henan Province (15HASTIT021), the Science and Technology Project of Henan Province (142300410114), and the Foundation of Henan Educational Committee (13A520017).
Conflict of interest
The authors declared that they have no conflicts of interest to this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Guo, T., Xiong, J. A new global fuzzy fault-tolerant control for a double inverted pendulum based on time-delay replacement. Neural Comput & Applic 29, 467–476 (2018). https://doi.org/10.1007/s00521-016-2576-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-016-2576-1