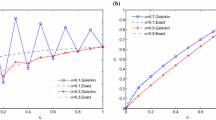
Abstract
The advection–dispersion phenomenon can be observed in various fields of science. Mathematically, this process can be studied by considering empirical models, high-order differential equations, and fractional differential equations. In this paper, a fractional model considered to represent the transport of passive tracers carried out by fluid flow in a porous media is studied both in the direct and inverse contexts. The studied mathematical model considers a one-dimensional fractional advection–dispersion equation with fractional derivative boundary conditions. The solutions of both direct and inverse problems are obtained by using the orthogonal collocation method and the differential evolution optimization algorithm approaches, respectively. In this case, the source term along the spatial and time coordinates is taken as a design variable. The obtained results with the solution of the direct problem are compared with those determined by using an implicit finite difference scheme. The results indicate that the proposed approach characterizes a promising methodology to solve the direct and inverse fractional advection–dispersion problems.







Similar content being viewed by others
References
Aslefallah M, Rostamy D (2014) A numerical scheme for solving space-fractional equation by finite differences theta-method. Int J Adv Appl Math Mech 1(4):1–9
Benítez T, Sherif SA (2017) Modeling spatial and temporal frost formation with distributed properties on a flat plate using the orthogonal collocation method. Int J Refrig 76:193–205
Benson DA, Wheatcraft SW, Meerschaert MM (2000) Application of a fractional advection-dispersion equation. Water Resour Res 36(6):1403–1412
Demirci E, Ozalp N (2012) A method for solving differential equations of fractional order. J Comput Appl Math 236:2754–2762
Ebrahimi AA, Ebrahim HA, Jamshidi E (2008) Solving partial differential equations of gas–solid reactions by orthogonal collocation. Comput Chem Eng 32:1746–1759
Ebrahimzadeh E, Shahrak MN, Bazooyar B (2012) Simulation of transient gas flow using the orthogonal collocation method. Chem Eng Res Des 90:1701–1710
Guo B, Xu Q, Yin Z (2016) Implicit finite difference method for fractional percolation equation with Dirichlet and fractional boundary conditions. Appl Math Mech 37(3):403–416
Gupta S, Kumar D, Singh J (2015) Numerical study for systems of fractional differential equations via Laplace transform. J Egypt Math Soc 23:256–262
Hernández-Calderón OM, Rubio-Castro E, Rios-Iribe EY (2014) Solving the heat and mass transfer equations for an evaporative cooling tower through an orthogonal collocation method. Comput Chem Eng 71:24–38
Jia J, Wang H (2015) Fast finite difference methods for space-fractional diffusion equations with fractional derivative boundary conditions. J Comput Phys 293:359–369
Jiang W, Lin Y (2010) Approximate solution of the fractional advection–dispersion equation. Comput Phys Commun 181:557–561
Kashan MH, Kashan AH, Nahavandi N (2013) A novel differential evolution algorithm for binary optimization. Comput Optim Appl 55:481–513
Kirchner JW, Feng X, Neal C (2000) Fractal stream chemistry and its implications for contaminant transport in catchments. Nature 403:524–526
Li X, Rui H (2018) A high-order fully conservative block-centered finite difference method for the time-fractional advection–dispersion equation. Appl Numer Math 124:89–109
Li C, Zhao T, Deng W, Wu Y (2014) Orthogonal spline collocation methods for the subdiffusion equation. J Comput Appl Math 255(1):517–528
Liang X, Yang Y-G, Gao F, Yang X-J, Xue Y (2018) Anomalous advection–dispersion equations within general fractional-order derivatives: models and series solutions. Entropy 20(1):78–85
Liu T, Hou M (2017) A fast implicit finite difference method for fractional advection-dispersion equations with fractional derivative boundary conditions. Adv Math Phys, 1–8
Magin RL (2006) Fractional calculus in bioengineering. Begell House Publishers, New York
Meerschaert MM, Tadjeran C (2004) Finite difference approximations for fractional advection–dispersion flow equations. J Comput Appl Math 172(1):65–77
Podlubny I (1999) Fractional differential equations. Academic Press, San Diego
Rehman M, Khan RA (2012) A numerical method for solving boundary value problems for fractional differential equations. Appl Math Model 36:894–907
Risken H (1984) Fokker-Planck equation: methods of solution and applications. Springer, Berlin, Heidelberg
Sabatelli L, Keating S, Dudley J, Richmond P (2002) Waiting time distributions in financial markets. Eur Phys J B 27:273–275
Schumer R, Benson DA, Meerschaert MM, Baeumer B (2003) Multiscaling fractional advection–dispersion equation and their solutions. Water Resour Res 39:1022–1032
Singh S, Patel V, Singh V (2018) Application of wavelet collocation method for hyperbolic partial differential equations via matrices. Appl Math Comput 320:407–424
Sonmezoglu A (2015) Exact solutions for some fractional differential equations. Adv Math Phys 2015:1–10
Storn R, Price K (1995) Differential evolution: a simple and efficient adaptive scheme for global optimization over continuous spaces. Int Comput Sci Inst 12:1–16
Storn R, Price K, Lampinen JA (2005) Differential evolution—a practical approach to global optimization. Springer—natural computing series. Springer, Berlin
Szekeres BJ, Izsák F (2015) A finite difference method for fractional diffusion equations with Neumann boundary conditions. Open Math 13:581–600
Villadsen J, Michelsen ML (1978) Solution of differential equation models by polynomial approximation. Prentice-Hall, Englewood Cliffs
Villadsen JV, Stewart WE (1967) Solution of boundary-value problems by orthogonal collocation. Chem Eng Sci 22:1483–1501
Yang X-J, Gao F, Machado JAT, Baleanu D (2017a) A new fractional derivative involving the normalized sinc function without singular kernel. Eur Phys J Spec Top 226:3567–3575
Yang X-J, Machado JAT, Baleanu D (2017b) Exact traveling-wave solution for local fractional boussinesq equation in fractal domain. Fractals 25(4):1740006
Yang X-J, Machado JAT, Nieto JJ (2017c) A new family of the local fractional PDEs. Fundam Inform 151:63–75
Yang X, Zhang H, Xu D (2018a) Orthogonal spline collocation method for the fourth-order diffusion system. Comput Math Appl 75:3172–3185
Yang X-J, Gao F, Ju Y, Zhou H-W (2018b) Fundamental solutions of the general fractional-order diffusion equations. Math Methods Appl Sci. 41:9312–9320
Yang X-J, Feng Y-Y, Cattani C, Inc M (2019) Fundamental solutions of anomalous diffusion equations with the decay exponential kernel. Math Methods Appl Sci 42:1–7
Yıldırım A, Koçak H (2009) Homotopy perturbation method for solving the space-time fractional advection–dispersion equation. Adv Water Resour 32:1711–1716
Yuan ZB, Nie YF, Liu F, Turner I, Zhang GY, Gu YT (2016) An advanced numerical modeling for Riesz space fractional advection–dispersion equations by a meshfree approach. Appl Math Model 40:7816–7829
Zhang J (2018) A stable explicitly solvable numerical method for the Riesz fractional advection–dispersion equations. Appl Math Comput 332:209–227
Zhang X, Liu L, Wu Y, Wiwatanapataphee B (2017) Nontrivial solutions for a fractional advection–dispersion equation in anomalous diffusion. Appl Math Lett 66:1–8
Acknowledgements
The authors are thankful for the financial support provided to the present research effort by CAPES, CNPq (574001/2008-5, 304546/2018-8, 439126/2018-5 and 431337/2018-7), FAPEMIG (TEC-APQ-3076-09, TEC-APQ-02284-15, TEC-APQ-00464-16, and PPM-00187-18), and CAPES through the INCT-EIE.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest.
Additional information
Communicated by V. Loia.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Lobato, F.S., Lima, W.J., Borges, R.A. et al. The solution of direct and inverse fractional advection–dispersion problems by using orthogonal collocation and differential evolution. Soft Comput 24, 10389–10399 (2020). https://doi.org/10.1007/s00500-019-04541-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-019-04541-y