Abstract
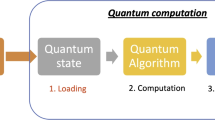
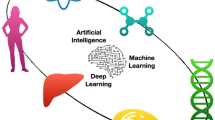
In the past few decades, researchers have extensively investigated the applications of quantum computation and quantum information to machine learning with remarkable results. This, in turn, has led to the emergence of quantum machine learning as a separate discipline, whose main goal is to transform standard machine learning algorithms into quantum algorithms which can be implemented on quantum computers. One further research programme has involved using quantum information to create new quantum-like algorithms for classical computers (Sergioli et al. in Int J Theor Phys 56(12):3880–3888, 2017; PLoS ONE 14:e0216224, 2019. https://doi.org/10.1371/journal.pone.0216224; Int J Quantum Inf 16(8):1840011, 2018a; Soft Comput 22(3):691–705, 2018b). This brief survey summarises and compares both approaches and also outlines the main motivations behind them.


Similar content being viewed by others
Notes
It should be stressed that quantum-like algorithms implemented by the NQiML approach are not a mere translation of classical algorithms. For instance, in Sergioli et al. (2018b, Section 2.1), the author introduces a quantum-like version of the NMC, which is very different from a mere quantum-theoretic translation of the NMC.
For instance, a very usual pre-processing consists in the normalisation of all the vectors of the dataset.
References
Aaronson S (2007) The learnability of quantum states. Proc R Soc Lond A Math Phys Eng Sci 463:3089–3114
Aïmeur E, Brassard G, Gambs S (2006) Machine learning in a quantum world. In: Conference of the Canadian Society for Computational Studies of Intelligence. Springer, Berlin
Audenaert KMR, Calsamiglia J, Munoz-Tapia R, Bagan E, Masanes LI, Acin A, Verstraete F (2017) Discriminating states: the quantum Chernof bound. Phys Rev Lett 98:160501
Bergou J, Herzog U, Hillery M (2004) Discrimination of quantum states. In: Lectures notes in Physics, vol 649. Springer, Berlin, pp 417–465
Bisio A, Chiribella G, Mauro G, Ariano D, Facchini S, Perinotti P (2010) Optimal quantum learning of unitary transformation. Phys Rev A 82(3):032324
Carrasquilla J, Melko RG (2017) Machine learning phases of matter. Nat Phys 13:431–434
Castelvecchi D (2017) IBM’s quantum cloud computer goes commercial. Nature 543(7664):159
Chefles A (2000) Quantum state discriminator. Contemp Phys 41(6):401–424
Dalla Chiara ML, Giuntini R, Leporini R, Negri E, Sergioli G (2015) Quantum information, cognition and music. Front Psychol 6:1583
Deutsch D (1985) Quantum theory, the Church–Turing principle and the universal quantum computer. Proc R Soc Lond A 400:97–117
Duda RO, Hart PE, Stork DG (2000) Pattern classification, 2nd edn. Wiley Interscience, New York
Feynamn R (1982) Simulating physics with computers. Int J Theor Phys 21(6/7):467–488
Freytes H, Sergioli G (2014) Fuzzy approach for Toffoli gate in quantum computation with mixed states. Rep Math Phys 74(2):159–180
Gambs S (2008) Quantum classification. arXiv:0809.0444v2
Guta M, Kotlowski W (2010) Quantum learning: asymptotically optimal classification of qubit states. New J Phys 12:123032
Hayashi A, Horibe M, Hashimoto T (2005) Quantum pure-state identification. Phys Rev A 72(5):052306
Helstrom CW (1976) Quantum detection and estimation theory. Academic Press, New York
Hilbert M, Lopez P (2011) The World’s technological capacity to store, communicate, and compute information. Science 332:60
Holik F, Sergioli G, Freytes H, Plastino A (2017) Pattern recognition in non-Kolmogorovian structures. Found Sci 23(1):119–132
Lloyd S, Mohseni M, Rebentrost P (2013) Quantum algorithms for supervised and unsupervised machine learning. arXiv:1307.0411
Lloyd S, Mohseni M, Rebentrost P (2014) Quantum principal component analysis. Nat Phys 10(9):631–633
Lu S, Braunstein SL (2014) Quantum decision tree classifier. Quantum Inf Process 13(3):757–770
Manju A, Nigam MJ (2014) Applications of quantum inspired computational intelligence: a survey. Artif Intell Rev 42(1):79–156
Melkikh AV, Khrennikov A, Yampolskiy RV (2019) Quantum metalanguage and new cognitive synthesis. NeuroQuantology 17:72–96
Nielsen MA, Chuang IL (2010) Quantum computation and quantum information, 10th Anniversary edn. Cambridge University Press, Cambridge
Qiu D (2007) Minimum-error discrimination between mixed states. arXiv:0707.3970 [quant-phis]
Santucci E (2017) Quantum minimum distance classifier. Entropy 19(12):659
Santucci E, Sergioli G (2018) Classification problem in a quantum framework. In: Khrennikov A, Bourama T (eds) Quantum foundations, probability and information, proceedings of the quantum and beyond conference, Vaxjo, Sweden, 13–16 June 2016. Springer, Berlin, Germany, in press
Sasaki M, Carlini A (2002) Quantum learning and universal quantum matching machine. Phys Rev A 66(2):022303
Schuld M, Petruccione F (2018) Supervised learning with quantum computers. In: Quantum science and technology. Springer, Berlin
Schuld M, Sinayskiy I, Petruccione F (2014a) An introduction to quantum machine learning. Contemp Phys 56(2):172–185
Schuld M, Sinayskiy I, Petruccione F (2014b) The quest for a quantum neural network. Quantum Inf Process 13(11):2567–2586
Schuld M, Fingerhuth M, Petruccione F (2017) Implementing distance-based classifier with a quantum interference circuit. Europhys Lett 119(6):60002
Sergioli G, Santucci E, Didaci L, Miszczak J, Giuntini R (2016) A quantum-inspired version of the nearest mean classifier. Soft Comput 22(3):691–705
Sergioli G, Bosyk GM, Santucci E, Giuntini R (2017) A quantum-inspired version of the classification problem. Int J Theor Phys 56(12):3880–3888
Sergioli G, Santucci E, Didaci L, Miszczak JA, Giuntini R (2018a) A quantum inspired version of the NMC classifier. Soft Comput 22(3):691–705
Sergioli G, Russo G, Santucci E, Stefano A, Torrisi SE, Palmucci S, Vancheri C, Giuntini R (2018b) Quantum-inspired minimum distance classification in biomedical context. Int J Quantum Inf 16(8):1840011
Sergioli G, Giuntini R, Freytes H (2019) A new quantum approach to binary classification. PLoS ONE 14:e0216224. https://doi.org/10.1371/journal.pone.0216224
Trugenberg CA (2002) Quantum pattern recognition. Quantum Inf Process 1(6):471–493
Wiebe N, Kapoor A, Svore KM (2015) Quantum nearest-neighbor algorithms for machine learning. Quantum Inf Comput 15(34):318–358
Wittek P (2014) Quantum machine learning: what quantum computing means to data mining. Academic Press, New York
Acknowledgements
I warmly thank Claudio Ternullo for the careful linguistic revision of the last version of the manuscript.
Funding
This work has been partially supported by the Project “Strategies and Technologies for Scientific Education and Dissemination” (CUP No. F71I17000330002) founded by Fondazione di Sardegna.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author does not have any conflicts of interest.
Ethical standard
This article does not contain any studies with human participants performed by any of the authors.
Additional information
Communicated by F. Holik.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Sergioli, G. Quantum and quantum-like machine learning: a note on differences and similarities. Soft Comput 24, 10247–10255 (2020). https://doi.org/10.1007/s00500-019-04429-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00500-019-04429-x