Method with horizontal fuzzy numbers for solving real fuzzy linear systems

Abstract

The paper presents a method for solving real fuzzy systems of linear equations with the usage of horizontal fuzzy numbers (HFNs). Based on the multidimensional RDM interval arithmetic and a fuzzy number in a parametric form, the definition of a horizontal fuzzy number with nonlinear left and right borders was given. Additionally, the paper presents the properties of basic algebraic operations on these numbers. The usage of horizontal fuzzy numbers with linear and nonlinear borders was illustrated in the examples with $n \times n$ fuzzy linear systems. The obtained results are multidimensional and satisfy the fuzzy linear systems. Calculated solutions of fuzzy linear systems were compared with the results of other methods. The solution obtained with horizontal fuzzy numbers satisfies any equivalent form of fuzzy linear system, whereas the results of existing methods do not satisfy the equivalent forms of the system. The presented examples also show that the method with HFN delivers a full multidimensional solution (direct solution). The analyzed results of standard methods, which are only a part of span (indicator, indirect solution) of a full solution and/or include values that do not satisfy the fuzzy linear systems, are underestimated or overestimated. The proposed method gives a possibility to obtain a crisp solution together with a crisp system of equations; other methods do not possess these properties.

1 Introduction

Fuzzy sets and fuzzy arithmetic play an important role in the problems where variables are uncertain. It helps to describe real problems in the form of mathematical models and finds a solution of tasks with uncertain variables. Fuzzy arithmetic and fuzzy sets are used in the uncertainty theory (Bhiwani and Patre 2009), computing with words (Zadeh 2002), grey systems (Liu and Forest 2010), granular computing (Pedrycz et al. 2008).

The idea of fuzzy numbers and arithmetic on fuzzy numbers was first presented in (Chang and Zadeh 1972; Mizumoto and Tanaka 1976; Dubois and Prade 1978). Currently, the most popular and often used fuzzy numbers have vertical form and are used to solve, e.g., fuzzy equations (Bhiwani and Patre 2009; Buckley and Qu 1990; Buckley et al. 2002), fuzzy nonlinear equations with an uncertain variable (Abbasbandy and Asady 2004; Dymova 2010; Jafarian and Nia 2013). However, fuzzy systems of linear equations describe systems from the real world with parameters that are rather fuzzy than crisp numbers. These systems appear in different areas, for example in mathematics, engineering, physics and economics. The usage of fuzzy numbers for solving fuzzy system of linear equations is presented in, e.g., (Abbasbandy and Alavi 2005; Abbasbandy and Jafarian 2006; Behera and Chakraverty 2012; Dehghan et al. 2006; Friedman et al. 1998; Jafari et al. 2009; Yeh 2007; Lodwick and Dubois 2015); in these papers the triangular or trapezoidal fuzzy numbers are considered. In Boroujeni et al. (2015), the method for solving the fuzzy systems of dual form with triangular fuzzy numbers is presented.

The standard fuzzy arithmetic is based on vertical fuzzy sets (Aliev et al. 2012; Dubois and Prade 1978; Hanss 2005; Klir 1997; Nguyen 2006; Rajati and Mendel 2012; Rajati et al. 2011; Zadeh 1996, 2002, 2007). Unfortunately, there were gaps because more complicated operations on the vertical representation of fuzzy numbers, e.g., a solution of fuzzy system of linear equations, provide the results that are not a full solution or are just a span of the solution (indirect result). Standard methods give the results which preclude obtaining the crisp solutions that satisfy the system of equations. Existing versions of fuzzy arithmetic assume that only vertical fuzzy number is the result of operations on fuzzy numbers. This assumption leads to many computational paradoxes observed in fuzzy arithmetic.

Why is the differentiation of direct and indirect solution important? Because the use of indirect results (e.g., span $[\underline{x}, \overline{x}])$, leads to imprecise, false or partly false solution. In Example 1, the differences between the results obtained by standard interval arithmetic (S-IA) and multidimensional RDM interval arithmetic were shown. The concept of the multidimensional Relative Distance Measure interval arithmetic (RDM-IA) was developed by A. Piegat (Piegat and Landowski 2013, 2017b; Landowski 2015, 2017).

Example 1

Solve interval equation $AX+B=AB$, where $A=[1,2]$ and $B=[4,6]$.

Standard interval arithmetic (S-IA)

$$\begin{aligned} X= & {} (AB-B)/A=([1,2][4,6]-[4,6])/[1,2]\\= & {} ([4,12]-[4,6])/[1,2]=[-2,8] / [1,2] =[-2,8] . \end{aligned}$$

Solution X does not satisfy the equation.

RDM interval arithmetic—multidimensional solution

Intervals A and B in RDM notation have a form: $A=1+\alpha _A$, $B=4+2\alpha _B$, where $\alpha _A$, $\alpha _B \in [0,1]$.

$$\begin{aligned} X= & {} (AB-B)/A=[(1+\alpha _A) (4+2\alpha _B) \\&- (4+2\alpha _B)] / (1+\alpha _A) =(4\alpha _A + 2\alpha _A \alpha _B)/(1+\alpha _A),\\&\quad \alpha _A, \alpha _B \in [0,1]. \end{aligned}$$

RDM solution $X(\alpha _A,\alpha _B)$ satisfies the equation. It is true solution of the equation.

Deriving span from RDM solution

$$\begin{aligned} s(X) = [\mathop {\min }\limits _{\alpha _A ,\alpha _B } X(\alpha _A ,\alpha _B ),\mathop {\max }\limits _{\alpha _A ,\alpha _B } X(\alpha _A ,\alpha _B )] = [0,3] \end{aligned}$$

Spans comparison

The S-IA gives span $s(X)=[-2,8]$, span with the RDM-IA equals $s(X) = [0,3]$.

Conclusions of Example 1:

• 1. The solution’s span calculated according to S-IA is usually considerably greater than the span calculated with RDM-IA.

• 2. Condition of the correct span determining is possessed by the multidimensional RDM arithmetic.

• 3. The solution span does not have to be calculated stepwise, sequentially as in the case of S-IA. It should be calculated only on the basis of the full multidimensional RDM solution.

To fill the gaps, the article presents the method with the usage of horizontal fuzzy number (HFN) to find the solution of fuzzy system of linear equations.

The main contributions of the paper are as follows:

• 1. In the paper, the definition and the examples of the horizontal fuzzy number where the left and right borders can be nonlinear were presented. The previous papers (Piegat and Landowski 2015, 2017a, c) considered only triangular and trapezoidal horizontal fuzzy numbers.

• 2. The proofs of the properties of basic algebraic operations on horizontal fuzzy numbers are given.

• 3. The paper presents the multidimensional approach to the solution of the fuzzy linear system. The proposed method gives a possibility to solve the fuzzy linear systems with various types of fuzzy numbers, not only with triangular or trapezoidal fuzzy numbers.

• 4. The presented method gives the multidimensional solution which has a possibility of generation of every crisp solution of the fuzzy systems of linear equations and can also generate crisp system of linear equations from fuzzy linear system for the considered crisp solution.

• 5. In the article, it is shown that in multidimensional approach the solution of the fuzzy system of linear equations in a vertical fuzzy number form is only the secondary information (indicator); the direct solution is a multidimensional set.

• 6. The examples show that the methods in the cited papers do not give full solutions and/or generate results that do not satisfy the equivalent forms of the fuzzy linear systems. The proposed method gives full solutions which satisfy the fuzzy systems of linear equations and their equivalent forms.

The correctness of the results obtained in the examples is easy to check by substituting calculated values to a given problem. Many researchers do not check the correctness of the results in presented examples. This way of comparing of the obtained solutions by method with horizontal fuzzy numbers with results by other methods is called the testing point method (TP method). By using the TP method, the points in incorrect solution that does not satisfy the fuzzy linear system or points that are solutions but are not included in the obtained results can be found.

2 Horizontal fuzzy number

In the following section, the theoretical foundations of the horizontal fuzzy number and its arithmetic are presented.

In RDM interval arithmetic, a given value x from interval $X = \left[ {\underline{x} ,\overline{x} } \right]$ is described using RDM variable $\alpha _x$, where $\alpha _x \in [0,1]$, as shown in (1).

$$\begin{aligned} x = \underline{x} + \alpha _x (\overline{x} - \underline{x}) \end{aligned}$$

(1)

Definition 1

(Landowski 2015) In notation RDM, the interval $X=\left[ {\underline{x} ,\overline{x} } \right]$ is described as a set of numbers given by (2).

$$\begin{aligned} X=\{x: x = \underline{x} + \alpha _x (\overline{x} - \underline{x}), \ \alpha _x \in [0,1] \} \end{aligned}$$

(2)

A fuzzy number in a parametric form is defined as intervals for every r-cut.

Definition 2

(Friedman et al. 1998) An arbitrary fuzzy number is an ordered pair of functions $(\underline{u} (r), \overline{u} (r))$, $0\le r \le 1$, which satisfy the following requirements:

• 1. $\underline{u} (r)$ is a bounded left continuous nondecreasing function over [0, 1].

• 2. $\overline{u} (r)$ is a bounded left continuous nonincreasing function over [0, 1].

• 3. $\underline{u} (r) \le \overline{u} (r)$, $0\le r \le 1$.

Fuzzy number is a model of uncertain value of variable.

Based on RDM interval notation and parametric definition of fuzzy number, a horizontal fuzzy number with linear or/and nonlinear left and right borders can be defined as:

Definition 3

A horizontal fuzzy number $U^r$ of an arbitrary fuzzy number $(\underline{u} (r), \overline{u} (r))$ is a set of numbers $u^r$ for every $r,\alpha _u \in [0,1]$ given by (3).

$$\begin{aligned} {U^r} {=} {\{u^r \in \mathbb {R}: u^r = \underline{u} (r) + \alpha _u (\overline{u} (r) - \underline{u} (r)),}{ r, \alpha _u \in [0,1] \} } \end{aligned}$$

(3)

The variable $\alpha _u$ gives a possibility to obtain any value between left border $\underline{u} (r)$ and right border $\overline{u} (r)$ of a fuzzy number. For $\alpha _u = 0$ value of the left endpoint $\underline{u} (r)$ of s fuzzy number and for $\alpha _u = 1$ the right endpoint $\overline{u} (r)$ of a fuzzy number are obtained.

The four basic arithmetic operations $* \in \{+,-,\cdot ,/\}$ on horizontal fuzzy numbers $U^r= \{u^r : u^r = \underline{u} (r) + \alpha _u (\overline{u} (r) - \underline{u} (r)), r, \alpha _u \in [0,1] \}$ and $V^r=\{v^r : v^r = \underline{v} (r) + \alpha _v (\overline{v} (r) - \underline{v} (r)), r, \alpha _v \in [0,1] \}$ are defined as set (4), operation  /  occurs only if $0 \notin V^r$.

$$\begin{aligned} \begin{array}{lll} {U^r*V^r} &{} {=} &{} {\{u^r*v^r:}\\ &{}&{} { u^r*v^r=[\underline{u} (r) + \alpha _u (\overline{u} (r) - \underline{u} (r))]}\\ &{} &{} { *[\underline{v} (r) + \alpha _v (\overline{v} (r) - \underline{v} (r))],}\\ &{}&{} { r, \alpha _u,\alpha _v \in [0,1]\} }\\ \end{array} \end{aligned}$$

(4)

The horizontal fuzzy number (HFN) $U^r = \{u^r \in \mathbb {R}: u^r = \underline{u} (r) + \alpha _u (\overline{u} (r) - \underline{u} (r)), r, \alpha _u \in [0,1] \}$ can be written as $u(r,\alpha _u)$ defined by Eq. (5)

$$\begin{aligned} u(r,\alpha _u)=\underline{u} (r) + \alpha _u (\overline{u} (r) - \underline{u} (r)), \end{aligned}$$

(5)

where $r, \alpha _u \in [0,1]$.

Definition 4

(The direct solution) The direct solution of operation on n horizontal fuzzy numbers $u_1(r, \alpha _{u_1})$, $\ldots ,$$u_n(r, \alpha _{u_n})$, where r, $\alpha _{u_1}$, $\ldots$, $\alpha _{u_n} \in [0,1]$, is a set of numbers expressed in the form of multidimensional formula $Z^r=z(r,\alpha _{u_1},\ldots , \alpha _{u_n})$ with up to n HFN variables $\alpha _{u_1}$, $\ldots$, $\alpha _{u_n} \in [0,1]$.

Example 2

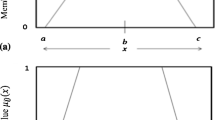
(Asady 2013) The fuzzy numbers A and B with nonlinear left and right borders, in parametric form $A=(-10+20r^{1/4},14-4r^3)$ and $B= (1+\sqrt{r}, 30 -27 \sqrt{r})$, $r\in [0,1]$, as horizontal fuzzy numbers are:

$$\begin{aligned} a(r, \alpha _a)= -10+20r^{1/4} + \alpha _a (24 -4r^3 - 20 r ^{1/4}), \end{aligned}$$

and

$$\begin{aligned} b(r,\alpha _b )= 1+\sqrt{r}+ \alpha _b ( 29-28 \sqrt{r}) \end{aligned}$$

where $\alpha _a$, $\alpha _b$, $r\in [0,1]$. Figures 1 and  2 show fuzzy numbers A and B in standard and horizontal forms.

Fig. 1

Fuzzy number $A=(-10+20r^{1/4},14-4r^3)$ in standard (a) and horizontal (b) form

Fig. 2

Fuzzy number $B= (1+\sqrt{r}, 30 -27 \sqrt{r})$ in standard (a) and horizontal (b) form

Basic operations on horizontal fuzzy numbers $X^r$, $Y^r$ and $Z^r$ hold the algebraic properties.

Both horizontal fuzzy number addition and multiplication are commutative and associative. For three HFNs $X^r=x(r,\alpha _x)$, $Y^r=y(r,\alpha _y)$ and $Z^r=z(r,\alpha _z)$, where $\alpha _x$, $\alpha _y$, $\alpha _z$, $r \in [0,1]$, Eq. (6) hold.

$$\begin{aligned} X^r+Y^r= & {} Y^r+X^r \nonumber \\ X^r \cdot Y^r= & {} Y^r \cdot X^r \nonumber \\ X^r + (Y^r + Z^r)= & {} (X^r + Y^r ) + Z^r \nonumber \\ X^r \cdot (Y^r \cdot Z^r)= & {} (X^r \cdot Y^r ) \cdot Z^r \end{aligned}$$

(6)

Proof

$X^r+Y^r=x(r,\alpha _x) + y(r,\alpha _y) = y(r,\alpha _y) + x(r,\alpha _x) = Y^r+X^r$, $X^r \cdot Y^r =x(r,\alpha _x) \cdot y(r,\alpha _y) = y(r,\alpha _y) \cdot x(r,\alpha _x) =Y^r \cdot X^r$, $X^r+(Y^r+Z^r)=x(r,\alpha _x) + [y(r,\alpha _y) + z(r,\alpha _z)] = [x(r,\alpha _x) + y(r,\alpha _y)] + z(r,\alpha _z) = (X^r+Y^r)+Z^r$, $X^r \cdot (Y^r \cdot Z^r) =x(r,\alpha _x) \cdot [y(r,\alpha _y) \cdot z(r,\alpha _z)] = [x(r,\alpha _x) \cdot y(r,\alpha _y)] \cdot z(r,\alpha _z) = (X^r \cdot Y^r ) \cdot Z^r$$\square$

In horizontal fuzzy number arithmetic, there exist neutral elements of addition and multiplication. For addition the neutral element is a degenerate fuzzy number 0; for multiplication the neutral element is a degenerate fuzzy number 1. For any fuzzy horizontal number $X^r$ hold Eq. (7).

$$\begin{aligned} X^r + 0= & {} 0 + X^r = X^r \nonumber \\ X^r \cdot 1= & {} 1 \cdot X^r = X^r \end{aligned}$$

(7)

The horizontal fuzzy number $X^r = x(r,\alpha _x)=\underline{x} (r) + \alpha _x (\overline{x} (r) - \underline{x} (r))$, where $r, \alpha _x \in [0,1]$, in HFN arithmetic has an additive inverse element (8).

$$\begin{aligned} -X^r = - x(r,\alpha _x)= -\underline{x} (r) - \alpha _x (\overline{x} (r) - \underline{x} (r)) \end{aligned}$$

(8)

Proof

$X^r+(-X^r)=[x(r,\alpha _x)]+[-x(r,\alpha _x)]=[\underline{x} (r) + \alpha _x (\overline{x} (r) - \underline{x} (r))] + [ -\underline{x} (r) - \alpha _x (\overline{x} (r) - \underline{x} (r)] = 0$ $\square$

In HFN arithmetic, there exists a multiplicative inverse element, so for $X^r = x(r,\alpha _x)=\underline{x} (r) + \alpha _x (\overline{x} (r) - \underline{x} (r))$, where $r, \alpha _x \in [0,1]$, $0\notin X^r$, the multiplicative inverse element is (9).

$$\begin{aligned} 1/X^r = 1/[ x(r,\alpha _x)]= 1/[\underline{x} (r) + \alpha _x (\overline{x} (r) - \underline{x} (r))] \end{aligned}$$

(9)

Proof

$X^r \cdot (1/X^r)=x(r,\alpha _x) \cdot [1/(x(r,\alpha _x))]= [\underline{x} (r) + \alpha _x (\overline{x} (r) - \underline{x} (r))] / [\underline{x} (r) + \alpha _x (\overline{x} (r) - \underline{x} (r))] = 1$ $\square$

In HFN arithmetic for every HFNs $X^r=x(r,\alpha _x)$, $Y^r=y(r,\alpha _y)$ and $Z^r=z(r,\alpha _z)$, where $\alpha _x$, $\alpha _y$, $\alpha _z$, $r \in [0,1]$, the distributive law holds, Eq. (10).

$$\begin{aligned} X^r(Y^r + Z^r) = X^r Y^r + X^r Z^r \end{aligned}$$

(10)

Proof

$X^r (Y^r + Z^r) = x(r,\alpha _x) \cdot [y(r,\alpha _y) + z(r,\alpha _z)]= x(r,\alpha _x) \cdot y(r,\alpha _y) + x(r,\alpha _x) \cdot z(r,\alpha _z) = X^r Y^r + X^r Z^r$ $\square$

The cancelation law for addition (11) holds for horizontal fuzzy numbers.

$$\begin{aligned} X^r + Z^r = Y^r + Z^r \Rightarrow X^r = Y^r \end{aligned}$$

(11)

Proof

For any horizontal fuzzy numbers $X^r=x(r,\alpha _x)$, $Y^r=y(r,\alpha _y)$ and $Z^r=z(r,\alpha _z)$, where $\alpha _x$, $\alpha _y$, $\alpha _z$, $r \in [0,1]$.

$$\begin{aligned} X^r + Z^r= & {} Y^r + Z^r, x(r,\alpha _x) + z(r,\alpha _z) \\= & {} y(r,\alpha _y) + z(r,\alpha _z). \end{aligned}$$

Adding to the both sides additive inverse element $-Z^r=-z(r,\alpha _z)$ there is:

$$\begin{aligned}&x(r,\alpha _x) + z(r,\alpha _z) +[-z(r,\alpha _z)] = y(r,\alpha _y) + z(r,\alpha _z) \\&\quad +[-z(r,\alpha _z)], x(r,\alpha _x) = y(r,\alpha _y) , X^r = Y^r \end{aligned}$$

$\square$

Also, for horizontal fuzzy numbers the multiplicative cancelation law (12) holds if $0\notin Z^r$.

$$\begin{aligned} X^r \cdot Z^r = Y^r \cdot Z^r \Rightarrow X^r = Y^r \end{aligned}$$

(12)

Proof

For any horizontal fuzzy numbers $X^r=x(r,\alpha _x)$, $Y^r=y(r,\alpha _y)$ and $Z^r=z(r,\alpha _z)$, where $\alpha _x$, $\alpha _y$, $\alpha _z$, $r \in [0,1]$, $0\notin Z^r$.

$$\begin{aligned} X^r \cdot Z^r= & {} Y^r \cdot Z^r,\\ x(r,\alpha _x) \cdot z(r,\alpha _z)= & {} y(r,\alpha _y) \cdot z(r,\alpha _z). \end{aligned}$$

Multiplying the obtained equation by multiplicative inverse element $1/Z^r=1/[z(r,\alpha _z)]$ there is:

$$\begin{aligned}&x(r,\alpha _x) \cdot z(r,\alpha _z) \cdot \{1/[z(r,\alpha _z)]\} \\&\quad =y(r,\alpha _y) \cdot z(r,\alpha _z) \cdot \{1/[z(r,\alpha _z)]\},\\&\qquad x(r,\alpha _x) = y(r,\alpha _y) , X^r = Y^r \end{aligned}$$

$\square$

The direct solution obtained with horizontal fuzzy numbers is presented by formula (granule of information), and also solution can be shown by result indicators (indirect solutions) like span, cardinality distribution or the center of gravity.

Definition 5

(span, secondary solution) For the direct solution $Z^r=z(r,\alpha _{u_1},\ldots , \alpha _{u_n})$ of the basic arithmetic operations on n horizontal fuzzy numbers span is a fuzzy number given by (13).

$$\begin{aligned} \begin{array}{l} s(Z^r)= (\mathop {\min }\limits _{\alpha _{u_1 } , \ldots ,\alpha _{u_n } } {z(r,\alpha _{u_1},\ldots , \alpha _{u_n})} ,\\ \qquad \qquad \qquad \qquad \mathop {\max }\limits _{\alpha _{u_1 } , \ldots ,\alpha _{u_n } } {z(r,\alpha _{u_1},\ldots , \alpha _{u_n})} )\\ \end{array} \end{aligned}$$

(13)

The special cases of fuzzy numbers are triangular $U=(a,b,c)$ and trapezoidal $V=(a,b,c,d)$ fuzzy numbers. Their parametric forms are $(\underline{u}(r), \overline{u}(r))=(a+(b-a)r,c+(b-c)r)$ and $(\underline{v}(r), \overline{v} (r))=(a+(b-a)r,d+(c-d)r)$, respectively, where $r \in [0,1]$. The triangular and trapezoidal horizontal fuzzy numbers are presented in Piegat and Landowski (2015, 2017a) as:

$$\begin{aligned} u(r,\alpha _u ) =[a+(b-a)r]+[(c-a)-r (c-a)]\alpha _u \end{aligned}$$

and

$$\begin{aligned} v(r,\alpha _v)=[a+(b-a)r]+ [(d-a)-r (d-a+b-c)]\alpha _v, \end{aligned}$$

where r, $\alpha _u$, $\alpha _v \in [0,1]$.

3 Solution of fuzzy linear systems with horizontal fuzzy numbers

Definition 6

(Abbasbandy and Alavi 2005; Friedman et al. 1998) (Fuzzy Linear System) The $n\times n$ linear system (14)

$$\begin{aligned} \begin{array}{*{20}c} {a_{11} x_1 + \cdots + a_{1n} x_n = y_1 } \\ {a_{21} x_1 + \cdots + a_{2n} x_n = y_2 } \\ \vdots \\ {a_{n1} x_1 + \cdots + a_{nn} x_n = y_n } \\ \end{array} \end{aligned}$$

(14)

where the coefficients matrix $A=(a_{ij})$, $1 \le i,j \le n$ is a $n\times n$ matrix and each $y_i$, $1 \le i \le n$, is a fuzzy number in parametric form which is called a fuzzy linear system in parametric form (FLS).

Steps to find the solution and the span of solution (indicator of solution) by the method with horizontal fuzzy numbers are as follows:

• Step 1: Write the given fuzzy numbers in algebraic system of equations in the HFN notation using HFN variables.

• Step 2: Calculate direct solution using algebraic operations.

• Step 3: To obtain span (indirect solution, indicator, secondary solution) of the solution find border values for HFN variable of the solution.

• Step 4: For border values find minimum and maximum that are span (secondary solution, indicator) of the direct solution.

4 Examples of solving fuzzy linear systems with horizontal fuzzy numbers

Example 3

(Friedman et al. 1998; Behera and Chakraverty 2012) Find a solution of $2\times 2$ fuzzy system of linear equation (15)

$$\begin{aligned} x_1 - x_2= & {} (r,2 - r), \nonumber \\ x_1 + 3x_2= & {} (4 + r,7 - 2r). \end{aligned}$$

(15)

In HFN notation, the fuzzy system of Eq. (15) has a form of (16),

$$\begin{aligned} x_1 - x_2= & {} r+ \alpha _1( 2 - 2r), \nonumber \\ x_1 + 3x_2= & {} 4 + r + \alpha _2 (3 - 3r ), \end{aligned}$$

(16)

where $r, \alpha _1, \alpha _2 \in [0,1]$.

The direct solution of fuzzy linear system (15) in HFN form is given by (17),

$$\begin{aligned} x_1(r,\alpha _1,\alpha _2)= & {} 1 + r + 1.5\alpha _1 (1 - r) + 0.75\alpha _2 (1 - r) \nonumber \\ x_2(r,\alpha _1,\alpha _2)= & {} 1 - 0.5\alpha _1 (1 - r) + 0.75\alpha _2 (1 - r) \end{aligned}$$

(17)

where $r, \alpha _1, \alpha _2 \in [0,1]$.

Figure 3 shows solution (17) of fuzzy system of linear equations in three-dimensional space.

Fig. 3

Three-dimensional horizontal fuzzy number solution of fuzzy system of linear equations, where $r\in [0:0.1:1]$

Substituting the obtained solution (17) to fuzzy system of Eq. (15) shows that the solution is correct, there is:

$x_1 - x_2 = 1 + r + 1.5\alpha _1 (1 - r) + 0.75\alpha _2 (1 - r) - [ 1 - 0.5\alpha _1 (1 - r) + 0.75\alpha _2 (1 - r)]= r + \alpha _1 (2 - 2r) = (r,2 - r)$, $x_1 + 3x_2 = 1 + r + 1.5\alpha _1 (1 - r) + 0.75\alpha _2 (1 - r) + 3 [ 1 - 0.5\alpha _1 (1 - r) + 0.75\alpha _2 (1 - r) ] = 4 + r + \alpha _2 (3 - 3r) = (4 + r,7 - 2r) .$

The direct solution of given fuzzy linear system (15) is presented by formula (17); every pair $(x_1(r,\alpha _1,\alpha _2),$$x_2(r, \alpha _1, \alpha _2))$ of solution depends on HFN variable $\alpha _1$, $\alpha _2 \in [0,1]$ and $r \in [0,1]$. For $2 \times 2$ fuzzy interval systems, point (crisp) solutions are coupled and cannot be considered separately.

The representation of the solution can be a span, but span is only the result indicator. Any two values from the span are not a pair of crisp solution. The choice of the crisp solution is possible for unique HFN variable $\alpha _1, \alpha _2 \in [0,1]$. For example, from formula (17) one of the crisp point solutions is a pair of numbers $(x_1(0.5,0,0),$$x_2(0.5,0,0)) = ( 1.5 , 1)$, $r =0.5$.

To find the span of the solution, border values should be calculated. Table 1 presents border values solution (17) for variables $\alpha _1$ and $\alpha _2$.

Table 1 Border values of solution with horizontal fuzzy numbers for HFN variable $\alpha _1$, $\alpha _2 \in [0,1]$ and $r\in [0,1]$

Considering the spans of (17), the solution $x_1 (r, \alpha _1,$$\alpha _2)$ has a minimum value for $\alpha _1 = \alpha _2 = 0$ and maximum for $\alpha _1 = \alpha _2 = 1$, solution $x_2 (r,\alpha _1,\alpha _2)$ has a minimum for $\alpha _1 = 1$ and $\alpha _2 = 0$ and maximum for $\alpha _1 =0$ and $\alpha _2 = 1$. The spans of (17) in parametric form are presented by (18) and in graphical form in Fig. 4,

$$\begin{aligned} s( x_1(r,\alpha _1,\alpha _2))= & {} (1 + r , 3.25 - 1.25r) \nonumber \\ s( x_2(r,\alpha _1,\alpha _2))= & {} (0.5+0.5r, 1.75-0.75r) \end{aligned}$$

(18)

where $r \in [0,1]$.

Fig. 4

Span of horizontal fuzzy number solution of fuzzy system of linear equations

The result for fuzzy system of linear equations (15) obtained by Friedman et al. (1998) and Behera and Chakraverty (2012) equals (19),

$$\begin{aligned} x_1= & {} (1.375 +0.625r,2.875-0.875r) \nonumber \\ x_2= & {} (0.875+0.125r, 1.375- 0.375r) \end{aligned}$$

(19)

where $r \in [0,1]$.

The results (19) satisfy the fuzzy system of linear equations only in the form of (15), but do not satisfy equivalent fuzzy linear system, for example in the form of (20).

$$\begin{aligned} x_1= & {} (r,2 - r) + x_2, \nonumber \\ x_1= & {} (4 + r,7 - 2r) - 3x_2. \end{aligned}$$

(20)

Substituting $x_1$ and $x_2$ from (19) to the right side of the equations of the fuzzy linear system in the form of (20) is:

$$\begin{aligned}&(r,2 - r) + x_2 = (r,2 - r) + (0.875+0.125r, \\&\qquad 1.375- 0.375r) = (0.875+1.125r, 3.375- 1.375r) \\&\quad \ne (1.375 +0.625r,2.875-0.875r)=x_1,\\&(4 + r,7 - 2r) - 3x_2 = (4 + r,7 - 2r) \\&\quad - 3 (0.875+0.125r, 1.375- 0.375r) \\&\quad = (-0.125 -0.125r, 4.375 - 2.375 r) \\&\quad \ne (1.375 +0.625r,2.875-0.875r) = x_1. \end{aligned}$$

Similarly it can be shown that results (19) do not satisfy other forms of fuzzy linear system (15).

The solution obtained with horizontal fuzzy number (17) satisfies any equivalent form of fuzzy linear system (15) and the universality conditions.

Results (19) are just spans (indicators, indirect solutions). From (19), it is difficult to find a pair of $(x_1,x_2)$ that satisfies the system of Eq. (15).

Spans of solutions (17) for $r=0$ are $s(x_1 ^{r=0} ) = (1,3.25)$, $s(x_2 ^{r=0} )=( 0.5,1.75)$ and the supports in (19) equal $x_1 ^{r=0} =(1.375, 2.875)$, $x_2 ^{r=0} = (0.875, 1.375)$. As it can be seen, the spans for $r=0$ in the solution obtained using horizontal fuzzy number have wider width than result (19). Result (19) is not a full span of solution of system (15); it can checked by testing point method. For example, from (17) for $r=0$, $\alpha _1 = 0.9$ and $\alpha _2 = 0.2$ values $x_1= 2.5$ and $x_2 = 0.7$ are one of the solutions of (15), but $x_2 = 0.7$ does not belong to “solution” (19).

Example 4

(Friedman et al. 1998; Behera and Chakraverty 2012) Find a solution of $3\times 3$ fuzzy system of linear equations (21),

$$\begin{aligned} x_1 + x_2 - x_3= & {} (r,2 - r), \nonumber \\ x_1 - 2 x_2 +x_3= & {} (2 + r,3), \nonumber \\ 2x_1 + x_2 + 3 x_3= & {} ( -2, -1- r), \end{aligned}$$

(21)

where $r \in [0,1]$.

The fuzzy system (21) using fuzzy horizontal number has a form of (22),

$$\begin{aligned} x_1 + x_2 - x_3= & {} r+ \alpha _1 (2-2r) , \nonumber \\ x_1 - 2 x_2 +x_3= & {} 2 + r + \alpha _2 (1-r), \nonumber \\ 2x_1 + x_2 + 3 x_3= & {} -2 + \alpha _3 (1-r), \end{aligned}$$

(22)

where $r, \alpha _1, \alpha _2, \alpha _3 \in [0,1]$.

The direct solution with horizontal fuzzy numbers is given by (23),

$$\begin{aligned} {x_1(r,\alpha _1,\alpha _2,\alpha _3)} =&\, [-\,6-11r-14\alpha _1 (1-r) \nonumber \\&-\,4 \alpha _2 (1-r) - \alpha _3 (1-r)]/(-\,13) , \nonumber \\ {x_2(r,\alpha _1,\alpha _2,\alpha _3)} =&\,[14+4r - 2\alpha _1 (1-r) \nonumber \\&+5 \alpha _2 (1-r) - 2 \alpha _3 (1-r) ] /(-\,13) , \nonumber \\ {x_3(r,\alpha _1,\alpha _2,\alpha _3) } =&\, [8+6r + 10 \alpha _1 (1-r) \nonumber \\&+ \alpha _2 (1-r) - 3 \alpha _3 (1-r)]/(\,-13), \end{aligned}$$

(23)

where $r, \alpha _1, \alpha _2, \alpha _3 \in [0,1]$.

By equations in (23), every three numbers $x_1$, $x_2$ and $x_3$ that satisfy the fuzzy system of linear equations (21) can be found.

It can be proved that solution (23) is corrected by substituting (23) to the fuzzy system of equations (21). For the first equation starting from the left side:

$$\begin{aligned}&x_1 + x_2 - x_3 = [-\,6-11r-14\alpha _1 (1-r) -4 \alpha _2 (1-r) \\&\quad -\,\alpha _3 (1-r)]/(-13) + [14+4r - 2\alpha _1 (1-r) \\&\quad +\,5 \alpha _2 (1-r) - 2 \alpha _3 (1-r) ] /(-13) \\&\quad -\, [8+6r + 10 \alpha _1 (1-r) + \alpha _2 (1-r) \\&\quad - \,3 \alpha _3 (1-r)]/(-13) = r+ \alpha _1 (2-2r) = (r,2 - r), \end{aligned}$$

the right side is obtained.

Similarly, it can be shown that solution (23) satisfies the second and third equations, so the solution obtained using horizontal fuzzy numbers satisfies the fuzzy system of linear equations (21) and also its equivalent form.

The solutions of fuzzy linear systems are dependent. The point solution of three values that satisfy the fuzzy system of linear equations (21) can be calculated from the solution with horizontal fuzzy numbers (23). For example, for $r=0$, $\alpha _1 = \alpha _3 = 0$ and $\alpha _2= 1$ from solution (23) the point solution is $(x_1,x_2,x_3)= (10/13,-19/13, -9/13)$.

For $r\in [0,1]$ the minimum and maximum values can be calculated. Table 2 presents border values of solution (23) for variables $\alpha _1$, $\alpha _2$ and $\alpha _3$.

Table 2 Border values of solution with horizontal fuzzy numbers for variables $\alpha _1$, $\alpha _2$, $\alpha _3 \in [0,1]$ and $r\in [0,1]$

The span (indicator, indirect solution) of solution (23) for $r \in [0,1]$ and RDM variables from Table 2 is presented by (24).

$$\begin{aligned}&s(x_1(r,\alpha _1,\alpha _2,\alpha _3))\nonumber \\&\quad = (6/13+11r/13, 25/13 - 8r/13) \nonumber \\&s(x_2(r,\alpha _1,\alpha _2,\alpha _3))\nonumber \\&\quad = (-19/13 +r/13, -10/13 -8r/13) \nonumber \\&s(x_3(r,\alpha _1,\alpha _2,\alpha _3))\nonumber \\&\quad = (-19/13 +5r/13, -5/13-9r/13) \end{aligned}$$

(24)

Figure 5 shows graphical form of spans (24) of solution with horizontal fuzzy numbers.

Fig. 5

Spans of horizontal fuzzy number solutions of $3\times 3$ fuzzy system of linear equations

The solution of the fuzzy system (21) obtained in (Friedman et al. 1998; Behera and Chakraverty 2012) according to M. Friedman et al. is not fuzzy numbers and cannot be used in practice because $\overline{x}_2 \le \underline{x}_2$ and $\overline{x}_3 \le \underline{x}_3$. Lodwick and Dubois (2015) wrote that improper intervals are not accepted. Changing the borders in $x_2$ and $x_3$, the indicator of “solution” is obtained. M. Friedman et al. called these results as a “weak solution” in a form of (25), but it can only be called the “weak indicator of solution”.

$$\begin{aligned} x_1= & {} (-\,30/13+47r/13,61/13-44r/13) \nonumber \\ x_2= & {} (-\,21/13+3r/13, -8/13-10r/13) \nonumber \\ x_3= & {} (-\,38/13 + 24r/13,14/13-28r/13 ) \end{aligned}$$

(25)

Results (25) from (Friedman et al. 1998; Behera and Chakraverty 2012) do not satisfy fuzzy linear system (21). Substituting $x_1$, $x_2$ and $x_3$ from (25) to the left side of fuzzy system of linear equations (21), there is:

$$\begin{aligned}&x_1 + x_2 - x_3 =(-30/13+47r/13, 61/13-44r/13) \\&\qquad +\, (-21/13 + 3r/13, -8/13 - 10r/13) \\&\qquad -\, (-38/13 + 24r/13, 14/13 - 28r/13 ) \\&\quad =\,(-65/13+78r/13, 91/13-78r/13) \ne (r,2 - r), \\&x_1 - 2 x_2 +x_3 = (-30/13+47r/13, 61/13-44r/13) \\&\qquad -\,2(-21/13 + 3r/13, -8/13-10r/13) \\&\qquad +\, (-38/13 + 24r/13, 14/13 - 28r/13 ) \\&\quad =\,(-52/13+91r/13, 117/13 - 75r/13) \ne (2 + r,3), \\&2x_1 + x_2 + 3 x_3 =2(-30/13 + 47r/13, 61/13-44r/13) \\&\qquad +\,(-21/13+3r/13, -8/13 - 10r/13) \\&\qquad +\, 3 (-38/13 + 24r/13, 14/13 - 28r/13 ) \\&\quad =\, ( -\,195/13 + 169r/13, 156/13 - 182r/13 ) \\&\quad \ne ( -\,2, -\,1-\, r). \end{aligned}$$

Also results (25) do not satisfy any fuzzy linear system equivalent to (21).

To compare results (23) and (25), spans (indirect solutions) for $r=0$ are presented in Table 3.

Table 3 Spans for $r=0$ of the solution obtained using horizontal fuzzy numbers and of the “weak solution” by methods presented in (Friedman et al. 1998; Behera and Chakraverty 2012)

Obtained fuzzy numbers in (Friedman et al. 1998; Behera and Chakraverty 2012) include values that are not a solution, and it is difficult to indicate the three points of solution of fuzzy linear system (21). For example, let us consider crisp solution from the obtained results in (Friedman et al. 1998; Behera and Chakraverty 2012). For $r=0$ values $x_1=-2$, $x_2=-1.2$ and $x_3=1$ belong to the solution presented in Table 3 and in (25), but these values do not satisfy system (21):

$$\begin{aligned} -2+ (-1.2) -1= & {} -4.2 \notin (0,2);\\ -2-2 \cdot (-1.2)+1= & {} 1.4\notin (2,3);\\ 2\cdot (-2) + (-1.2) + 3 \cdot 1= & {} -2.2 \notin (-2,-1). \end{aligned}$$

Spans in the form of intervals of HFN solution in (24) and for $r=0$ in Table 3 are just the representations (indicators) of the full solution.

Values $(x_1,x_2,x_3)$ that satisfy the fuzzy linear system (21) should be calculated from (23). Solutions $x_1 (r,$$\alpha _1, \alpha _2, \alpha _3)$, $x_2(r,\alpha _1,\alpha _2,\alpha _3)$ and $x_3(r,\alpha _1,\alpha _2,\alpha _3)$ are dependent. Three numbers of the solution that satisfy system (21) can be obtained for unique HFN variables $\alpha _1$, $\alpha _2$, $\alpha _3 \in [0,1]$ and $r \in [0,1]$. For example, let us consider the crisp solution with HFN: values $x_1=1.5$, $x_2=-1$ and $x_3=-1.3$ calculated from the obtained solution (23) for $r=0$, $\alpha _1=0.9$, $\alpha _2=0.2$ and $\alpha _3=0.1$ satisfy system (21):

$$\begin{aligned} 1.5+ (-1) - (-1.3)= & {} 1.8 \in (0,2);\\ 1.5-2 \cdot (-1)+(-1.3)= & {} 2.2 \in (2,3);\\ 2\cdot (1.5) + (-1) + 3 \cdot (- 1.3)= & {} -1.9 \in (-2,-1). \end{aligned}$$

The data in example 5 were taken from SalooKolayi et al. (2011), where authors solved linear fuzzy model to plan the feeding of the animals.

Example 5

(SalooKolayi et al. 2011) Find the plan of a diet for animals by seven feeds. The chemical compositions of feeds are given in Table 4, where: E—energy, Pr—protein, F—fat, NDF—neutral detergent fiber, NFC—non-fibrous carbohydrate, Ca—calcium and P—phosphor.

Table 4 Chemical compositions of feeds (SalooKolayi et al. 2011)

The fuzzy values of nutrient requirements of feeds are presented in Table 5, $r \in [0,1]$.

Table 5 Fuzzy values of nutrient requirements (SalooKolayi et al. 2011)

To find the feeding plan the $7\times 7$ fuzzy system of linear equations (26) has to be solved,

$$\begin{aligned}&1190 x_1 + 1860 x_2 + 5020 x_3 + 1840 x_4 + 2130 x_5 + 1380 x_6 \nonumber \\&\quad +\, 1610 x_7 = (1480+40r,1700-100r)\nonumber \\&192 x_1 + 124 x_2 + 85 x_4 + 499 x_5 + 284 x_6 + 173 x_7\nonumber \\&\quad =\,(150+10r,190-20r) \nonumber \\&25 x_1 +22 x_2 + 845 x_3 + 2 x_4 + 16 x_5 + 14 x_6 + 43 x_7 \nonumber \\&\quad = \,(25+10r,90-20r)\nonumber \\&416 x_1 + 208 x_2 + 149 x_5 + 403 x_6 + 425 x_7\nonumber \\&\quad =\, (280+40r,420-40r)\nonumber \\&257 x_1+ 617 x_2 + 798 x_4 + 270 x_5 + 222 x_6 + 296 x_7\nonumber \\&\quad =\, (320+60r,440-40r) \nonumber \\&14.7 x_1 + 0.6 x_2 + 120 x_3 + 1.5 x_4 + 4 x_5 + 4.8 x_6 + 1.3 x_7\nonumber \\&\quad =\, (9.5+0.5r,10.5-0.5r) \nonumber \\&2.8 x_1 + 3.9 x_2 + 0.3 x_4 + 7.1 x_5 + 10 x_6 + 11.8 x_7 \nonumber \\&\quad =\, (4.75+0.25r,5.25-0.25r) \end{aligned}$$

(26)

where $r \in [0,1]$.

The fuzzy system (26) in the form of HFN notation, where $\alpha _1 , \ldots , \alpha _7, r \in [0,1]$, is presented by formula (27).

$$\begin{aligned}&1190 x_1 + 1860 x_2 + 5020 x_3 + 1840 x_4 + 2130 x_5 + 1380 x_6 \nonumber \\&\quad +\, 1610 x_7 = 1480 + 40r + (220 - 140r) \alpha _1\nonumber \\&192 x_1 + 124 x_2 + 85 x_4 + 499 x_5 + 284 x_6 + 173 x_7\nonumber \\&\quad =\, 150 + 10r + (40 - 30r) \alpha _2 \nonumber \\&25 x_1 +22 x_2 + 845 x_3 + 2 x_4 + 16 x_5 + 14 x_6 + 43 x_7 \nonumber \\&\quad = \,25 + 10r + (65 - 30r) \alpha _3 \nonumber \\&416 x_1 + 208 x_2 + 149 x_5 + 403 x_6 + 425 x_7\nonumber \\&\quad =\, 280 + 40r + (140 - 80r) \alpha _4 \nonumber \\&257 x_1+ 617 x_2 + 798 x_4 + 270 x_5 + 222 x_6 + 296 x_7\nonumber \\&\quad =\, 320 + 60r + (120- 100r) \alpha _5 \nonumber \\&14.7 x_1 + 0.6 x_2 + 120 x_3 + 1.5 x_4 + 4 x_5 + 4.8 x_6 + 1.3 x_7\nonumber \\&\quad =\, 9.5 + 0.5r+ (1 - r) \alpha _6 \nonumber \\&2.8 x_1 + 3.9 x_2 + 0.3 x_4 + 7.1 x_5 + 10 x_6 + 11.8 x_7 \nonumber \\&\quad =\, 4.75 + 0.25r + (0.5 - 0.5r) \alpha _7 \end{aligned}$$

(27)

Solving fuzzy system of equations (27), the multidimensional solutions $x_i$ ($i \in \{1,\ldots ,7\}$) of fuzzy system of linear equations (26) expressed in the form of HFN notation using variable $\alpha _i \in [0,1]$ and $r \in [0,1]$ were obtained. Direct solutions are presented by formula (28).

$$\begin{aligned}&x_1(r,\alpha _1,\ldots ,\alpha _7)=- 0.8642 r + 1.5729 \nonumber \\&\quad -\, 0.0043 \alpha _1(140r - 220) \nonumber \\&\quad +\, 0.0128 \alpha _2(30r - 40) + 0.0436 \alpha _3(30r - 65) \nonumber \\&\quad +\, 0.0004 \alpha _4(80r - 140) + 0.0086 \alpha _5(100r - 120) \nonumber \\&\quad -\, 0.1292 \alpha _6 (r - 1) + 0.0195 \alpha _7 (0.5r - 0.5) \nonumber \\&x_2(r,\alpha _1,\ldots ,\alpha _7) = 1.9747r - 2.6044 \nonumber \\&\quad +\, 0.0076 \alpha _1(140r - 220)\nonumber \\&\quad -\, 0.0271 \alpha _2(30r - 40) - 0.0982 \alpha _3(30r - 65)\nonumber \\&\quad -\, 0.0099 \alpha _4(80 r - 140) - 0.0153 \alpha _5(100r - 120)\nonumber \\&\quad + 0.3722 \alpha _6(r - 1) + 0.4134 \alpha _7(0.5r - 0.5) \nonumber \\&x_3(r,\alpha _1,\ldots ,\alpha _7) = 0.0617r - 0.0612 \nonumber \\&\quad +\, 0.0003 \alpha _1(140r - 220) \nonumber \\&\quad - \,0.0008 \alpha _2(30r - 40) - 0.0034 \alpha _3(30r - 65) \nonumber \\&\quad -\, 0.0001 \alpha _4(80r - 140) - 0.0005 \alpha _5(100r - 120) \nonumber \\&\quad +\, 0.0040 \alpha _6(r - 1) + 0.0006 \alpha _7(0.5r - 0.5) \nonumber \\&x_4(r,\alpha _1,\ldots ,\alpha _7) = - 0.8729r + 1.4080 \nonumber \\&\quad -\, 0.0033 \alpha _1(140r - 220) \nonumber \\&\quad +\, 0.0128 \alpha _2(30r - 40) + 0.0480 \alpha _3(30r - 65) \nonumber \\&\quad +\, 0.0060 \alpha _4(80r - 140) + 0.0053 \alpha _5(100r - 120) \nonumber \\&\quad -\, 0.2014 \alpha _6(r - 1) - 0.2452 \alpha _7(0.5r - 0.5) \nonumber \\&x_5(r,\alpha _1,\ldots ,\alpha _7) = - 0.5966r + 0.7205 \nonumber \\&\quad -\, 0.0029 \alpha _1(140r - 220) \nonumber \\&\quad +\, 0.0060 \alpha _2(30r - 40) + 0.0234 \alpha _3(30r - 65) \nonumber \\&\quad +\, 0.0018 \alpha _4(80r - 140) + 0.0061 \alpha _5(100r - 120) \nonumber \\&\quad -\, 0.0436 \alpha _6(r - 1) + 0.0083 \alpha _7(0.5r - 0.5) \nonumber \\&x_6(r,\alpha _1,\ldots ,\alpha _7) = 2.2621r - 2.7735 \nonumber \\&\quad +\, 0.0112 \alpha _1(140r - 220) \nonumber \\&\quad -\, 0.0330 \alpha _2(30r - 40) - 0.0956 \alpha _3(30r - 65) \nonumber \\&\quad -\, 0.0045 \alpha _4(80r - 140) - 0.0225 \alpha _5(100r - 120) \nonumber \\&\quad +\, 0.2043 \alpha _6(r - 1) + 0.0043 \alpha _7(0.5r - 0.5) \nonumber \\&x_7(r,\alpha _1,\ldots ,\alpha _7) = - 1.9622r + 2.7712 \nonumber \\&\quad -\, 0.0092 \alpha _1(140r - 220) \nonumber \\&\quad +\, 0.0299 \alpha _2(30r - 40) + 0.0878 \alpha _3(30r - 65) \nonumber \\&\quad +\, 0.0057 \alpha _4(80r - 140) + 0.0183 \alpha _5(100r - 120) \nonumber \\&\quad -\, 0.2341 \alpha _6(r - 1) - 0.2284 \alpha _7(0.5r - 0.5) \end{aligned}$$

(28)

The spans (indirect solutions) of solutions (28) of fuzzy system of equations (26) are presented in parametric form by (29) and graphically in Fig. 6,

$$\begin{aligned} s(x_1(r,\alpha _1,\ldots ,\alpha _7))= & {} (-\,2.87+1.73r,2.64-1.59r) \nonumber \\ s(x_2(r,\alpha _1,\ldots ,\alpha _7))= & {} (-\,4.89+3.64r,8.13-4.13r) \nonumber \\ s(x_3(r,\alpha _1,\ldots ,\alpha _7))= & {} (-\,0.13+0.1r,0.26-0.12r )\nonumber \\ s(x_4(r,\alpha _1,\ldots ,\alpha _7))= & {} (-\,3.72+1.97r,2.46-1.66r )\nonumber \\ s(x_5(r,\alpha _1,\ldots ,\alpha _7))= & {} (-\,2.04+1.05r,1.44-1.05r )\nonumber \\ s(x_6(r,\alpha _1,\ldots ,\alpha _7))= & {} (-\,5.46+4.05r,8.1-4.21r )\nonumber \\ s(x_7(r,\alpha _1,\ldots ,\alpha _7))= & {} (-\,7.15+3.87r,5.16-3.61r ) \nonumber \\ \end{aligned}$$

(29)

where $r \in [0,1]$.

Fig. 6

Spans of horizontal fuzzy numbers solution of fuzzy system of linear equations $7 \times 7$

In this case, where the solution is a plan of diet for animals obtained values should be greater than or equal to zero. So the values that satisfy this condition should be picked from the solution. With HFN method, the crisp solution where values are greater than or equal to zero can be obtained. One of this crisp solution equals $(x_1,x_2,x_3,x_4,$$x_5,x_6,x_7)= (0.29,0.22, 0.05, 0.05, 0, 0.13,0.15)$; it can be obtained for $r=0$, $\alpha _1 = 0$, $\alpha _2 = 0$, $\alpha _3 = 0.5$, $\alpha _4 = 0$, $\alpha _5 = 0$, $\alpha _6 = 1$ and $\alpha _7 = 0$. Because of the knowledge of the values r and $\alpha _i$, the system of linear equations for this crisp solution can be obtained.

Example 6

Let us consider the fuzzy system of linear equations (30) where the border values are not linear,

$$\begin{aligned} x_1 - x_2= & {} (1+r^2,4-r^3) \nonumber \\ 3 x_1 -2 x_2= & {} (3+2r^2, 6- \sqrt{r}) \end{aligned}$$

(30)

where $r \in [0,1]$.

The fuzzy numbers $M=(1+r^2,4-r^3)$ and $N=(3+2r^2, 6- \sqrt{r})$, using variables $\alpha _1 \in [0,1]$ and $\alpha _2 \in [0,1]$, in HFN notation have a form $m(r,\alpha _1)=1 + r^2 + \alpha _1 (3-r^2 - r^3 )$ and $n(r,\alpha _2) = 3+2r^2 +\alpha _2 (3- \sqrt{r} - 2 r^2)$, respectively.

The graphical presentation of fuzzy numbers M and N in standard and horizontal forms is shown in Figs. 7 and 8.

Fig. 7

Fuzzy number $M=(1+r^2,4-r^3)$ in standard (a) and horizontal (b) form

Fig. 8

Fuzzy number $N= (3+2r^2, 6- \sqrt{r})$ in standard (a) and horizontal (b) form

The fuzzy system of linear equations (30) with horizontal fuzzy numbers $m(r,\alpha _1)$ and $n(r,\alpha _2)$ is presented by (31),

$$\begin{aligned} x_1 - x_2= & {} 1 + r^2 + \alpha _1 (3-r^2 - r^3 ) \nonumber \\ 3 x_1 -2 x_2= & {} 3+2r^2 +\alpha _2 (3- \sqrt{r} - 2 r^2) \end{aligned}$$

(31)

where $\alpha _1, \alpha _2, r \in [0,1]$.

The direct solution of fuzzy system of linear equations (31) is given by (32),

$$\begin{aligned}&{x_1(r,\alpha _1,\alpha _2) = 1 - 2 \alpha _1 (3-r^2 - r^3 ) }\nonumber \\&\quad {+ \alpha _2 (3- \sqrt{r} - 2 r^2)}\nonumber \\&{x_2(r,\alpha _1,\alpha _2) = -r^2 - 3 \alpha _1 (3-r^2 - r^3 ) }\nonumber \\&\quad { +\alpha _2 (3- \sqrt{r} - 2 r^2 )} \end{aligned}$$

(32)

where $\alpha _1, \alpha _2, r \in [0,1]$.

Figure 9 shows solutions $x_1$ and $x_2$ in 3-dimensional space for $r\in [0:0.1:1]$ and $\alpha _1, \alpha _2 \in [0,1]$.

Fig. 9

Three-dimensional horizontal fuzzy number solution of fuzzy system of linear equations, where $r\in [0:0.1:1]$

The obtained solutions (32) satisfy the fuzzy system of linear equations (30). Substituting solutions (32) to the left side of (30), the correctness of the solution can be checked:

$$\begin{aligned} x_1 - x_2= & {} [1 - 2 \alpha _1 (3-r^2 - r^3 ) + \alpha _2 (3- \sqrt{r} - 2 r^2) ] \\&\quad -\, [-r^2 - 3 \alpha _1 (3-r^2 - r^3 ) \\&\quad +\,\alpha _2 (3- \sqrt{r} - 2 r^2) ] = 1+r^2\\&\quad +\, \alpha _1 (3 - r^2 - r^3 ) = (1+r^2 , 4-r^3), \\ 3x_1 - 2x_2= & {} 3 [1 - 2 \alpha _1 (3-r^2 - r^3 ) + \alpha _2 (3- \sqrt{r} - 2 r^2) ] \\&\quad -\, 2[-r^2 - 3 \alpha _1 (3-r^2 - r^3 ) \\&\quad +\,\alpha _2 (3- \sqrt{r} - 2 r^2) ] = 3+2r^2\\&\quad +\, \alpha _2 (3- \sqrt{r} - 2 r^2) = (3+2r^2, 6- \sqrt{r}) . \end{aligned}$$

The spans (indirect solutions) of the solution present (33) and are shown in graphical form in Fig. 10,

$$\begin{aligned} s(x_1(r,\alpha _1,\alpha _2))= & {} (-5 +2 r^2 +2 r^3, 4 - \sqrt{r} - 2 r^2) \nonumber \\ s(x_2(r,\alpha _1,\alpha _2))= & {} (-9 +2 r^2 +3r^3, 3 - \sqrt{r} - 3 r^2) \end{aligned}$$

(33)

where $r \in [0,1]$.

Fig. 10

Span of horizontal fuzzy number solution of fuzzy system of linear equations

Using solution (32) of fuzzy system of linear equations, any crisp solution with appropriate crisp system of linear equations can be generated. For example for $r=1$, $\alpha _1 = 0$ and $\alpha _2 =1$ the crisp solution equals $x_1=1$ and $x_2=-1$. From HFN notation of fuzzy system of linear equations (31), the crisp system of linear equations for the considered crisp solution can be obtained: $x_1-x_2=2$, $3x_1-2x_2=5$.

5 Conclusions

The paper presents a method with horizontal fuzzy number for solving fuzzy systems of linear equations. The definition and the examples of horizontal fuzzy number where border values are nonlinear were given. Also it was proved that operations on horizontal fuzzy numbers hold basic algebraic properties. The solved numerical examples show that the solution is multidimensional and satisfies fuzzy linear systems. The solutions calculated with horizontal fuzzy numbers are associated, which means that every crisp value of a solution corresponds with other crisp values of solutions.

The solution obtained with the proposed method with HFN variables gives a possibility to calculate a crisp solution and a crisp system of linear equations which corresponds with this solution. This possibility is impossible with the methods that use vertical fuzzy numbers, because in these cases the results do not bring any information about crisp solution. Also it was proved that the obtained multidimensional solution satisfies the fuzzy system of linear equations. Moreover, in the analyzed examples it was shown that the obtained results as fuzzy numbers in (Friedman et al. 1998; Behera and Chakraverty 2012) are not full solutions and are underestimated or overestimated.

Existing methods for solving fuzzy linear systems assume that the direct solution is a vertical fuzzy number. This assumption leads to paradoxes. In the article, it was shown that the result in a vertical fuzzy number form is only the secondary information (indicator, indirect solution) of the solution being a multidimensional set. The method with horizontal fuzzy numbers gives a correct full multidimensional solution.

To show the applicability of the proposed method also the practical fuzzy system of linear equations and system with a fuzzy number where borders are nonlinear were solved. The proposed method solves the fuzzy linear system given in different equivalent forms. The methods with vertical fuzzy numbers for equivalent forms of fuzzy linear systems give different results.