1 Introduction

River discharge data is considered as an important source of hydrological information and is used in a number of water resources engineering applications. Therefore, accurate modeling and estimation of streamflow process along with the development of new approaches and the improvement of available ones are of high importance (Mohammadi et al. 2006; Kisi and Shiri 2011). Two different general groups for streamflow models can be identified: physically-based and mathematically-based methods. The physically-based methods are sophisticated models that consider a number of parameters and hydro-meteorological variables that affect streamflow phenomena. On the other hand, mathematical methods represent data-driven models that simulate streamflow variations, as the dynamical models separately, based on previously recorded observations of streamflow data itself (Modarres and Ouarda 2013a). The latter models are simpler to apply in practice due to the easiness of their implementation (Karimi et al. 2015). A large number of data-driven techniques can be identified, such as artificial neural networks (ANN), adaptive neuro-fuzzy inference systems (ANFIS), genetic programming (GP), wavelet transforms (WT), support vector regression (SVR), and time series analysis (TSA) models, which have been receiving increasing attention in the field of water resources engineering (Wang et al. 2006, 2015; Ouachani et al. 2011; Liang et al. 2018).

The present work intends to demonstrate the abilities of linear and nonlinear multivariate /multiple time series techniques to model streamflows. The complete review and use of other techniques are beyond the scope of this paper. Among a number of TSA approaches, linear time series models, such as the autoregressive moving average (ARMA) model, have been widely applied for the modeling of different hydro-climatic variables, especially streamflows, and are also mainly based on univariate streamflow time series (Livina et al. 2003; Wang et al. 2004; Mohammadi et al. 2006; Modarres and Ouarda 2013b). Multiple time series approaches provide valuable methods for applying information embedded in multiple (multisite) measures which have dependent behaviors temporally and cross-sectionally (Salas et al. 1980; Tsay 2013). These approaches are not very often used to model streamflow data. Consequently, in the planning and management of water resources systems, it is common to involve several time series for modeling multivariate hydrological series (Salas et al. 1980; Hipel and McLeod 1996).

Multivariate time series approaches are used in several fields of applied sciences and engineering because of the notable potential for modeling the simultaneous temporal behavior of many variables (Niedzielski 2007). In hydrology science, a multivariate time series approach is considered as the multidimensional phenomenon which allows one to analyze complex relationships between hydrologic variables measured at dissimilar sites within a watershed but at the same climatic zone (Hipel and McLeod 1996; Niedzielski 2007). On the other hand, since the structure of streamflow processes is dynamic and complex, in order to properly model linear and nonlinear multiple time series, the use of multivariate techniques is inevitable. In this regard, these techniques provide a better understanding of the dynamic relationship between multiple streamflow time series and capture more precisely their joint dynamics and nonlinearity both in space and time.

Various multivariate models have been proposed in this regard by several researchers, namely, Matalas (1967), Matalas and Wallis (1971), and others in the early 1970s. Although multivariate hydrologic data are often modeled using ANN, ANFIS, GP and WT techniques (Dawson and Wilby 2001; Shu and Ouarda 2008; Wang et al. 2015), linear and nonlinear multiple time series approaches and their combinations have not been applied to modeling streamflow time series. The potential of multiple time series approaches has not been examined in depth, although their remarkable advantages in hydrologic modeling have been pointed out in a few studies (Niedzielski 2007). The recent review by Nigam et al. (2014) on stochastic runoff modeling approaches points out to the lack of multiple time series model applications, such as the vector AR (VAR) model, in the literature for streamflow analysis. Niedzielski (2007) recently applied a multiple AR method for peak discharge prediction in the Odra River in Poland.

The VAR approach is applied for modeling and forecasting the first moment (the mean behavior) of multiple time series. This approach is commonly inadequate for removing the nonlinear properties such as heteroscedasticity (or volatility) in hydrological data that is related to second order moment, or the conditional variance-covariance structure (Liu et al. 2011; Fathian et al. 2018). Therefore, to fit these nonlinear processes adequately, and to capture the dynamics of the series more precisely, other more complex models such as nonlinear modeling methods have to be considered (Järas and Gishani 2010). In general, a number of modern nonlinear models, which were developed in systems theory and econometrics, focus on conditional variance; see Tong (1990). One of the nonlinear time series models is the generalized autoregressive conditional heteroscedasticity (GARCH) approach which provides an appropriate framework for studying the heteroscedasticity issue. This model was introduced by Engle (1982) and developed by Bollerslev (1986) for modeling conditional variance in order to describe the change in the time-varying variance of economic time series (Wang et al. 2005). The multiple GARCH (MGARCH) approach, as an extended mode of the univariate GARCH approach, was introduced by Engle and Kroner (1995) for modeling dynamic relationships between time-varying variance processes concerning multiple time series.

As mentioned earlier, a VAR approach is considered to model the conditional mean of multiple time series (Tsay 2013). Although the residuals or the innovations of a VAR model may show adequacy, conditional variance (time-varying variance) or volatility may exist in the multiple residuals, which can be removed by an MGARCH model. One of the main advantages of this approach is that it can capture and stabilize the heteroscedasticity of the multiple residuals of a VAR model. In addition, this approach gives the “time-varying” association between multiple residual time series for each time step and investigates the persistence of the second order moment of the variables of interest as well as their association. However, the main disadvantage of the MGARCH modeling approach is that it increases the number of parameters of the time series model without ensuring a better prediction accuracy for the variables of interest. In other terms, time-varying variance is related to the squared residuals in the field of hydrology, which presents the existence of a behavior in the residuals known as the ARCH effect. The MGARCH approaches are being usually used to examine the conditional variance-covariance structure of financial time series (e.g., Chang et al. 2011). However, it seems that the nonlinear associations through variance-covariance of the multiple streamflow time series have not been fully investigated by MGARCH models in hydro-climatic studies. Recent efforts to use the multivariate GARCH approach upon some original hydro-climatic variables, not upon residuals time series that are extracted from multiple linear models, have been observed (Modarres and Ouarda 2013a, 2014a, b; Modarres et al. 2014).

The objectives of the present study are (1) to apply the VAR approach to model the mean behavior of multiple daily streamflow time series, (2) to model the ARCH effect in the multiple residuals extracted from the VAR approach to develop the nonlinear bivariate diagonal vectorization heteroscedasticity (DVECH) model, considered as one of the key MGARCH models, (3) to demonstrate the structure of conditional variance-covariance that exists in the multiple residuals, (4) to assess the performances of the VAR and VAR–DVECH approaches for modeling multiple streamflow time series using a number of appropriate evaluation criteria.

2 Study area and data

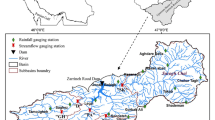
As a case study, the upstream subbasin of Zarrineh Rood dam is selected in this research as one of the largest subbasins of the Urmia Lake Basin. This subbasin is located south of Urmia Lake in northwestern Iran, with an area of 7081 km2 as shown in Fig. 1. The Zarrineh Rood River is the main source of the Lake’s water inflow from the south of Urmia Lake with approximately 230 km length (Fathian et al. 2015). The elevation of the study area varies between 1746 and 2121 m. The branches and all main tributaries of this river originate from the snow-covered mountains located in Kurdistan and West Azerbaijan provinces. The case study is constituted of Saghez Chai, Jighato Chai, Khorkhoreh Chai, and Sarogh Chai subbasins located from west to east, respectively (Fig. 1). The drainage lines of these subbasins discharge water into the reservoir of Zarrineh Rood dam (Fathian et al. 2018). In order to model streamflow processes, the six daily average streamflow data obtained from six hydrometric gauging stations are used. The length of the daily observations is 15 continuous years from 1 January 1997 to 31 December 2011. The data from 1 January 1997 to 31 December 2009 (4745 observations) were used for model calibration and the data from 1 January 2010 to 31 December 2011 (730 observations) were used for model validation. Figure 1 and Table 1 show the geographical distribution of the hydrometric gauging stations and their main properties, respectively. In the remainder of the paper, the abbreviations of the streamflow gauging stations are applied instead of their full names, as displayed in Table 1.

Fig. 1
figure 1

Locations of the rivers and their streamflow gauging stations in the study area

Full size image
Table 1 List of streamflow gauging stations used in this study
Full size table

3 Methods

3.1 VAR approach

The vector autoregressive (VAR) approach is one of the most widely applied forms of multiple time series approaches. This approach describes the dependency and interdependency of normalized data in time. A VAR approach with order p, VAR(p), as presented here, is given as follows Fathian et al. (2018):

$$z_{t} = \phi_{0} + \sum\limits_{i = 1}^{p} {\phi_{i} z_{t - i} } + a_{t}$$
(1)

where zt is the multiple hydrologic time series (more than one time series), ϕ0 is a k-dimensional constant vector, ϕi is a k × k matrix for i > 0, and at is a sequence of i.i.d random vectors with mean zero and covariance matrix Σa. For multivariate applications in hydrology, k can represent the number of stations. Equation 2 illustrates the form of this approach for the specific case of the bivariate VAR(1) model:

$$\begin{aligned} z_{1,t} & = \phi_{1,11} z_{1,t - 1} + \phi_{1,12} z_{2,t - 1} + a_{1,t} \\ z_{2,t} & = \phi_{1,21} z_{1,t - 1} + \phi_{1,22} z_{2,t - 1} + a_{2,t} \\ \end{aligned}$$
(2)

In this study, the deseasonalized modeling technique is used to acquire the normal and non-seasonal time series. For this purpose, two steps should be included. First, the logarithms of daily streamflows are calculated and a new time series is obtained. Second, the transformed times series is deseasonalized when the new time series are subtracted from the seasonal daily mean data and are divided by their own seasonal standard deviation. Moreover, before deseasonalization, streamflow series are smoothed using the Fourier harmonics to alleviate the stochastic variations of the daily means and standard deviations (Salas et al. 1980). After that, according to the structures of ACF (Auto-Correlation Function) and CCF (Cross-Correlation Function) concerning multiple series as well as the model selection criterion AIC (Akaike Information Criterion), the linear VAR-type approaches are fitted to the different multiple deseasonalized time series (Niedzielski 2007).

To check the model adequacy of a VAR approach, the structures of ACFs and CCF of the multiple residuals are first inspected. It should be noted that for an i.i.d series with length n, the lag k coefficients distribution of auto- and cross-correlation are normal with a mean zero and a variance 1/n, and a 95% confidence interval \(\pm 1.96/\sqrt n\). The model sufficiency of the fitted approach is not accepted when all coefficients of the ACFs and CCF don’t fall within the confidence intervals (Tsay 2013).

More formally, a multiple Ljung–Box test is also applied to test the sufficiency of the VAR model. This test computes a statistic Qk(m), which is χ2 distributed with (m − p)k2 degrees of freedom and is given as follows Tsay (2013):

$$Q_{k} (m) = T^{2} \sum\limits_{k = 1}^{m} {\frac{1}{T - k}tr\left( {\hat{R}_{k}^{{\prime }} \hat{R}_{0}^{ - 1} \hat{R}_{k} \hat{R}_{0}^{ - 1} } \right)}$$
(3)

where T is the sample size; m is the number of cross-correlation matrices of the multiple residuals, \(\hat{R}_{0}\) and \(\hat{R}_{k}\) are the lag zero and k sample of cross-correlation matrix relating to the multiple residuals, respectively, and the prime denotes the transpose of a matrix. The residuals are time-independent and the model is adequate if the statistic value Qk(m) is higher than the significant value. For more details concerning the model specification, estimation and diagnostic checking, the reader is referred to Box et al. (2008).

3.2 Multiple GARCH approach

3.2.1 Background

The MGARCH approach is generally used to model time series jointly that have multiple measurements. This approach explores the relationship between the conditional variance of a multiple time series in time (Francq and Zakoian 2011). For example, the present study aims to identify if there is a connection between the conditional variance in the twofold residuals that change through time, at, from a twofold streamflow series at different hydrometric stations.

The general MGARCH approach with a k-dimensional residuals matrix, \(a_{t} = (a_{1t} ,a_{2t} , \ldots ,a_{kt} )^{{\prime }}\), is given as follows:

$$E(a_{t} |F_{t - 1} ) = 0,\quad \varSigma_{t} = H_{t} = Cov(a_{t} |F_{t - 1} ) = E(a_{t} a_{t}^{{\prime }} |F_{t - 1} )$$
(4)
$$F_{t - 1} = \left\{ {a_{t - 1} ,a_{t - 2} , \ldots } \right\},\quad a_{t} |F_{t - 1} \sim\left( {0,\varSigma_{t} } \right)$$
(5)
$$a_{t} = H_{t}^{1/2} \varepsilon_{t}$$
(6)

where Ht is the conditional covariance matrix of at, given Ft−1 and ɛt is a k-dimensional i.i.d white noise (mean zero and identity covariance matrix) and. Let Ft−1 denote the σ-field generated by the past data {zt−i|i = 1, 2, …}. Then, it can be applied one form of the MGARCH approaches by describing the above conditional distribution of at. The readers can refer to Tsay (2010) and Francq and Zakoian (2011) for finding more details.

3.2.2 Diagonal VECH model

The diagonal VECH approach, called DVECH hereafter, was developed by Bollerslev et al. (1988) and represents one of the main types of the MGARCH approach. The VECH term presents the half-vectorization operator, which stacks the column of a square matrix from the diagonal downwards in a vector. The DVECH approach can be generally written as follows:

$$H_{t} = \omega + \sum\limits_{i = 1}^{m} {\varGamma_{i} \oplus ({\text{a}}_{t - i} {\text{a}}_{t - i}^{{\prime }} )} + \sum\limits_{j = 1}^{s} {G_{j} \oplus H_{t - j} }$$
(7)

where Γi and Gj are symmetric matrices, m and s are nonnegative integers, and ⊕ denotes the Hadamard product (element-by-element multiplication). A bivariate DVECH(1,1), for example, is given to illustrate the form of this approach as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {h_{11,t} } & {} \\ {h_{21,t} } & {h_{22,t} } \\ \end{array} } \right] & = \left[ {\begin{array}{*{20}c} {\omega_{11} } & {} \\ {\omega_{21} } & {\omega_{22} } \\ \end{array} } \right]\, + \left[ {\begin{array}{*{20}c} {\gamma_{11} } & {} \\ {\gamma_{21} } & {\gamma_{22} } \\ \end{array} } \right] \oplus \left[ {\begin{array}{*{20}c} {a_{1,t - 1}^{2} } & {} \\ {a_{1,t - 1} a_{2,t - 1} } & {a_{2,t - 1}^{2} } \\ \end{array} } \right] \\ & \quad + \left[ {\begin{array}{*{20}c} {g_{11} } & {} \\ {g_{21} } & {g_{22} } \\ \end{array} } \right] \oplus \left[ {\begin{array}{*{20}c} {h_{11,t - 1} } & {} \\ {h_{21,t - 1} } & {h_{22,t - 1} } \\ \end{array} } \right] \\ \end{aligned}$$
(8)

The number of parameters in the DVECH(1,1) model is equal to 3(k(k + 1)/2) and the matrix structure is as lower triangular. According to Eq. 6, it can be seen nine parameters to estimate for the bivariate mode. Here, h11,t and h22,t represent the conditional variances of streamflow series at the first and second hydrometric stations, respectively. Additionally, h21,t represents the conditional covariance (co-volatility) between those time series (Modarres and Ouarda 2014b).

3.2.3 Conditional heteroscedasticity test

One assumption for the residuals obtained from the VAR approach (as the linear multiple time series model) is that the residuals are time-invariant. It can be said in another way that if the conditional covariance matrix (Σt) is independent in time, then there is no conditional heteroscedasticity. However, the squared residual time series (or second-order moment) is occasionally autocorrelated. This behavior in these time series presents the existence of an ARCH effect. The presence of conditional heteroscedasticity or ARCH effect is checked using the Portmanteau test prior to volatility modeling. For sufficiently fixed m, the Ljung–Box Q * k (m)-statistic of the Portmanteau test is calculated as follows:

$$Q_{k}^{ * } (m) = T^{2} \sum\limits_{i = 1}^{m} {\frac{1}{T - i}b_{i}^{{\prime }} } (\hat{\rho }_{0}^{ - 1} \otimes \hat{\rho }_{0}^{ - 1} )b_{i}$$
(9)

where T denotes the sample size, k is the dimension of at, and \(b_{i} = vec(\hat{\rho }_{i}^{{\prime }} )\) with \(\hat{\rho }_{i}\) being the lag-i sample cross-correlation matrix of the squared residuals, a 2 t . Under the null hypothesis that at has no conditional heteroscedasticity, Q * k (m) is asymptotically distributed as \(\chi_{{k^{2} m}}^{2}\). It should be noted that Q * k (m) is asymptotically equivalent to the multivariate generalization of the Lagrange Multiplier (LM) test of Engle (1982) for conditional heteroscedasticity (Li 2004; Tsay 2013).

3.3 Experiments

In this section, the number of stations (k-dimension) should be chosen before applying the VAR and DVECH approaches for hydrologic modeling within the upstream basin of the Zarrineh Rood dam. Some experiments can be presented in order to compare the performances of the applied approaches. In the present study, the five distinct bivariate-experiments and a combination of both upstream and downstream stations were conducted (see Table 2). In another way, the five bivariate-VAR(p) and DVECH(m, s) approaches are applied for modeling, in which each of the experiments considers two stations (k = 2). The experiments are conducted independently.

Table 2 List of experiments used in this study
Full size table

3.4 Model comparison

The time series models used in the present study are evaluated through a multi-criteria comparison by applying a set of evaluation metrics for each of the experiments, independently. These evaluation metrics are, namely the absolute maximum error (AME), the peak difference (PDIFF), the root mean squared error (RMSE), the mean absolute error (MAE), the relative absolute error (RAE), and the coefficient of determination (R2). More details about the mathematical formulations of these criteria can be found in Modarres and Ouarda (2012, 2013b) and Fathian et al. (2016).

4 Empirical results and discussion

4.1 Modeling of VAR approach

In order to build a VAR model for the selected experiment, first, the order of the fitted model should be determined. For this purpose, the ACF of streamflows, CCF structure between two selected streamflow data and the obtained value of information criteria approach are checked. In the present study, experiment 1 as an example is used to demonstrate and describe the properties of the streamflow time series. Both of the two streamflows data in experiment 1 are related to flow series at the upstream (“GH” site) and downstream (“D” site) hydrometric stations, respectively. Figure 2a, b present the time series evolution of two original streamflows data of “GH” and “D” with their corresponding transformed (or standardized) time series as shown in Fig. 2c, d, respectively. According to the Fig. 2a, b, they are not detected any trend; however, the annual seasonalities are observed in these time series. The time series are transformed to the deseasonalized series using the standardization technique as shown in Fig. 2c, d.

Fig. 2
figure 2

Examples of daily streamflow (m3/s) of “GH” and “D” (a, b), and the corresponding standardized series (c, d)

Full size image

In the following, Fig. 3a–c demonstrate the ACF and CCF structures of the two daily time series. According to these figure, it can be observed a high persistence and non-stationarity behavior in those daily streamflow time series. By applying the standardization approach, persistence is reduced and the non-stationarity is removed (Fig. 3d–f). Moreover, the standardized series (Fig. 2c, d) show a fast decaying ACFs and CCF (Fig. 3d–f). This allows one to assume an autoregressive structure for the time series. For the VAR approach fitting procedure, finding out the statistical ACFs and CCFs behavior become the essential information on dependencies. Thus, this study attempts to fit a VAR approach to two standardized time series.

Fig. 3
figure 3

ACF and CCF plots for the daily streamflow time series recorded at “GH” and “D” stations; (a–c) analysis of the original data; (d–f) the analysis of the standardized data

Full size image

Among a number of candidates, the best fitted model for the adequacy is selected by trial and error for each experiment based on the minimum value of AIC and testing the multiple residuals of the fitted model. Therefore, the VAR models with orders 5, 9, 12, 5, and 7 for experiments 1–5, respectively, are fitted to the daily streamflows data. Figure 4a, as an example for experiment 1, show the adequacy of the fitted VAR(5) approach according to the multiple Ljung–Box test as all p-values are above the critical level (α = 0.05). In other words, as shown in Fig. 4b–d, there are no auto- and cross-correlation structures in the multiple residuals according to the ACF and CCF structures (as all coefficients fall within the confidence intervals).

Fig. 4
figure 4

aP-values of the multiple Ljung-Box test, b–d ACFs and CCF of the twofold residuals for VAR(5) model at “GH” and “D” stations

Full size image

Though the residual time series obtained from VAR approach seem to be visually and statistically uncorrelated (as mentioned in the above paragraph), the behavior of the auto-correlation coefficients of the squared multiple residuals were examined to control the existence of the ARCH effect. Figure 5a–c show the ACF and CCF structures of the squared residual time series. According to this figures, it can be confirmed the presence of conditional heteroscedasticity (or an ARCH effect) in the squared residuals from the fitted VAR(5) approach (as the auto- and cross-correlation coefficients fall outside the confidence limit at different lags). Figure 5d also show the existence of the conditional heteroscedasticity in the squared residual time series from the VAR(5) approach according to the p-values of the Portmanteau test. As seen, the p-values of this test are less than the critical value (α = 0.05) for all time lags; therefore, the alternative hypothesis of no ARCH effect is accepted. For this reason, applying a DVECH model to remove the heteroscedasticity from the multiple residual time series of the VAR approaches is essential for each experiment.

Fig. 5
figure 5

a–c ACFs and CCF of the squared twofold residuals for VAR(5) model, and dP-values of the Portmanteau test for squared twofold residuals at “GH” and “D” stations

Full size image

4.2 Multiple GARCH modeling

According to the preceding section, the conditional heteroscedasticity of the multiple residual time series of streamflows obtained from the VAR models was found to be significant. Therefore, we need to fit the bivariate DVECH approach to remove the conditional variance-covariance in the multiple residual time series. For each experiment, the bivariate DVECH approaches with different orders are tested for daily twofold residual time series. For experiments 1 to 5, the best fitted models are the bivariate DVECH(1,1), DVECH(3,1), DVECH(2,1), DVECH(1,1) and DVECH(3,1), respectively. These models were selected based on the minimum value of AIC. The adequacy of the DVECH approaches fitted to each experiment were verified using the inspection of ACF structure of the squared and cross-product standardized residual time series based on the suggestions by Tse (2002). Figure 6a–c, as an example, show the ACF structures of the squared standardized residual time series for “GH” and “D” stations and their cross-products for experiment 1. As seen, it is not observed any significant autocorrelation structure, in other words; all correlation coefficients at all lags (up to lag k = 25) are located between the confidence intervals. Therefore, there is no effect of conditional heteroscedasticity according to the null hypothesis acceptance.

Fig. 6
figure 6

a–c ACFs of the squared and cross-product standardized twofold residuals for the VAR(5)-DVECH(1,1) model at “GH” and “D” stations of experiment 1

Full size image

The maximum likelihood method was used to estimate the parameters of bivariate DVECH approaches. As shown in Table 3, these estimated parameters are significant at 95% confidence level. Moreover, the matrix of conditional variance-covariance residual time series, as an example for “GH” and “D” stations for experiment 1, can be given as follows:

$$\begin{aligned} h_{11,t} & = 0.080 + 0.274a_{1,t - 1}^{2} + 0.685h_{11,t - 1} \\ h_{21,t} & = 0.035 + 0.167a_{1,t - 1} a_{2,t - 1} + 0.773h_{21,t - 1} \\ h_{22,t} & = 0.069 + 0.175a_{2,t - 1}^{2} + 0.774h_{22,t - 1} \\ \end{aligned}$$
(10)

Figure 7 demonstrates the conditional variance (h11,t and h22,t) and their covariance (h21,t) behaviors of the residual time series for “GH” and “D” stations. Furthermore, Fig. 8 illustrates the conditional covariance behavior of other experiments such as “PG” versus “PA”, “S” versus “SK”, “GH” versus “PG”, and “D” versus “PA”.

Table 3 Parameters of the fitted bivariate DVECH models for each experiment
Full size table
Fig. 7
figure 7

Conditional variance–covariance matrix for “GH” and “D” time series (experiment 1) by DVECH model

Full size image
Fig. 8
figure 8

Estimated conditional covariance time series for experiments 2–5 by DVECH model

Full size image

The estimated parameters in Table 3 show that the conditional covariances obtained from DVECH approaches depend mainly on the lagged covariances instead of the cross-products of the lagged residual series. The intensity of persistency is measured by the γ + g term, which for the covariance of streamflow residual series take the values 0.940, 0.983, 0.910, 0.959 and 0.994 for all experiments, respectively. The highest covariance persistency is observed for “D” versus “PA” process and the lowest value belongs to “S” versus “SK” process. In addition, it can be observed a high persistency in the variance behavior of the streamflow residual series for all experiments. According to the obtained results, the persistency (γ + g) of the residuals conditional variance for upstream stations is higher than downstream ones for experiments 1 and 2. Thus, the conditional variance of the upstream station (“GH”), according to the Fig. 7, appears to be more dynamic than the downstream one (“D”). For experiments 4 and 5 that consider jointly the two upstream and downstream stations the persistency of conditional variances for all stations, except “PG” station, is higher than those stations for experiments 1 and 2. Moreover, the estimated parameters present that the long-term persistency (g) is much stronger than the short-term persistency (γ) in the conditional variance-covariance structure between twofold streamflow residuals’ series for all experiments. In addition, in the comparative assessment for all experiments, the measures of long-term persistency for upstream stations, which drain the smaller sub-basins, are lower than for downstream ones.

Figures 7 and 8 illustrate that the behavior of conditional covariances between twofold streamflow residual series for each experiment has a high level of temporal fluctuations. The amount and limits of the conditional variance differ from experiment to experiment and from time to time. As seen, the conditional covariances fluctuate continuously; so that, they increase happening very quickly after a minor decrease, and then remains typically high for a short time. Additionally, the amount of conditional covariances seems to become higher during 2003–2006 for experiments 3 and 4 than other time periods. For other experiments, these covariances remain at higher levels during all time periods.

In what follows, to explore the behavior of correlation coefficients of twofold streamflow residuals over time, the conditional correlation coefficients are estimated for each experiment (Fig. 9). As seen, for experiments 1 and 2 as well as for experiments 4 and 5, the conditional correlation coefficients have the same patterns. The behaviors of conditional correlation coefficients for each experiment demonstrate a high level of relationship between twofold streamflows. The average amounts of the correlation coefficients for experiments 1–5 are 0.43, 0.45, 0.16, 0.68 and 0.66, respectively. As observed in Fig. 9, these coefficients usually keep near or below the average amounts over all time periods. The correlation coefficients of the twofold streamflows for experiment 4 (“GH” vs. “PG”) and for experiment 5 (“D” vs. “PA”) are more than those of other experiments. These coefficients suggest high fluctuations and don’t keep on a fixed status. They have a tendency to vary very quickly from one position to the opposite position over time.

Fig. 9
figure 9

Estimated conditional correlation coefficients between bivariate streamflow innovation time series for all experiments by DVECH model

Full size image

4.3 Evaluation of model performance

The performance of the VAR and VAR-DVECH approaches applied to modeling twofold streamflows for each experiment are evaluated in this section using the evaluation criteria presented in Sect. 3.4. Prior to describing the evaluation criteria, the scatter plots, time series plots, and QQ plots of the observed against estimated twofold streamflows (for experiment 1: “GH” and “D”) were demonstrated for VAR and VAR–DVECH approaches in Figs. 10, 11 and 12, respectively. According to the Fig. 10, the performance of VAR–DVECH approach is better than the VAR in estimating streamflows with high amounts; however, the performance of the two approaches is good in estimating streamflows with low amounts. As seen in the high flow observations, the performance of the VAR and VAR–DVECH approaches are almost the same for the “GH” station that located in the upstream part of sub-basin. On the other hand, the fluctuations of high flow observations display the better performance of the VAR–DVECH approach for the “D” station located in the downstream part of the sub-basin; so that, the distribution of observational flows is around the best fitting line. In this region, the months of January–April as well as the months of November and December (in total about 180 days per year) represent the wet season. Since streamflows have high fluctuations due to the variations in the presence of rain and snow, all models underestimate high streamflow quantiles in this season. On the other hand, low flow quantiles are better estimated during the months of May to October (dry season) because the daily mean standard deviation fluctuations of streamflows are low in this season. The time series plots of the observed and estimated streamflows for “GH” and “D” stations, given in Fig. 11, also confirm the above explanations. A similar discussion was also reported by Modarres and Ouarda (2013b).

Fig. 10
figure 10

Scatter plot of observed versus estimated streamflows for a, c VAR and b, d VAR-DVECH models for “GH” and “D” stations for experiment 1

Full size image
Fig. 11
figure 11

Time series plot of the observed and estimated streamflows for a, c VAR and b, d VAR-DVECH models for “GH” and “D” stations for experiment 1

Full size image
Fig. 12
figure 12

QQ plots of the observed and estimated streamflows for VAR and VAR-DVECH models for “GH” and “D” stations for experiment 1

Full size image

The QQ plots also show that all models estimate the low flow quantiles better than the high flow quantiles (Fig. 12). It is observable that the departure of the estimated quantiles from the observed ones is almost the same as for the VAR and VAR–DVECH approaches in the upstream station “GH”. However, the high flow quantiles are better estimated for the VAR–MGARCH model at the downstream station “D”. Moreover, the departure of quantiles from the y = x line for the VAR–DVECH model is less than that of the VAR model for both “GH” and “D” stations. This indicates that the DVECH model can reduce the variation of the model output as well as the model estimation uncertainty.

In the following paragraphs, Table 4 presents the numerical evaluation criteria for all experiments to evaluate and compare the performance of the VAR and VAR–DVECH approaches. According to this table, the VAR–DVECH approach performs better than that of the VAR approach according to the applied statistics. Consequently, the VAR–DVECH approach can be termed as “very good” model efficiency classification of R2 as reported by Dawson et al. (2007). The VAR model is considered “satisfactory”, according to its R2 values. The AME criterion presents less error for the VAR approach than the VAR–DVECH approach for almost all experiments/stations. The PDIFF criterion that describe the error value in the estimation of peak streamflow for the VAR–DVECH approach is less than that of the VAR approach for experiments 1, 2 and 4, whereas this result is reversed for the rest of the experiments. Therefore, the VAR–DVECH approach that suggests less error than VAR approach is more acceptable in estimating maximum streamflows when one upstream and downstream station or both upstream stations are jointly considered. Moreover, the general agreement between observed and estimated high streamflows according to the Fig. 10 is better in the VAR–DVECH approach. Therefore, the VAR–DVECH approach is recognized as better model compared to the VAR approach. In this way, the main advantage of this model is the use of DVECH model to remove the heteroscedasticity of the twofold residuals of the VAR approach.

Table 4 Evaluation criteria of VAR and VAR-DVECH models for all experiments
Full size table

4.4 Discussion

The topic of conditional heteroscedasticity (time-varying variance or volatility) is usually ignored in the field of modeling hydro-climatic variable. The present study shows that even though the VAR approach seems to be sufficient for modeling the conditional mean of the multiple daily streamflow time series, there is still an effect of ARCH in the multiple residuals. Fitting the VAR model to the streamflow data sets used in this study, we observed the inadequacy of the VAR model for capturing the conditional variance of daily streamflows for all experiments that consider various twofold data sets jointly.

The exploration of the ARCH effect existence and the insufficiency of the VAR approach in removing this effect is outside of the scope of the present study. However, the present of ARCH effect in daily streamflows may be partly due to the seasonal fluctuation in variances as reported by Wang et al. (2005). Other factors that may prove the presence of ARCH effect in hydrological time series are such as the perturbations of air temperature fluctuations, an influential factor for snowmelt, and variations of evapotranspiration and precipitation as dominant factors in streamflow processes. Similar reports have been presented by Modarres and Ouarda (2012, 2013b) about the reasons of this effect. In these reports, the conditional heteroscedasticity may be the result of the atmospheric and climatic factors that influence the variance variation of the hydrologic time series. Additionally, the heteroscedasticity term of the residuals may reveal the effect of physical characteristics of watershed such as rate of infiltration, drainage area, time of concentration, and surface abstraction.

The DVECH approach showed the ability of modeling conditional variance-covariance. On the other hand, this approach improved the performance of the VAR approach according to the multi-criteria error evaluation. This result can be an important aspect of streamflow time series modeling in the regions that consider some hydro gauging stations within the same climatic zone but at dissimilar sites. The normalization, as discussed in Sect. 4.1, can be a helpful transformation method to reduce the variance of streamflows as well as the uncertainty of model estimation as reported by Modarres and Ouarda (2012, 2013b). As a result, this study show that the DVECH model together with a proper transform can increase the performance of the vector time series approaches and stabilize the conditional heteroscedasticity.

In the case of structure of conditional variance-covariance and correlation, Modarres and Ouarda (2013a) presented that physical feature of watershed may affect the existence of the time-varying variance in the residuals. On the other hand, the presence of the conditional correlations in the residuals may be related to the driving factors behind excess runoff production such as the basin storage properties and soil moisture, which delay the generated excess runoff from reaching the drainage network.

5 Conclusions

Prior to our study, multiple linear and nonlinear time series approaches had not yet been applied to model the conditional mean behavior for multiple hydrology processes and to investigate the conditional variance–covariance behavior for innovations of multiple hydrology processes. In this study, we developed these approaches, namely, VAR and diagonal VECH models, to model the time-varying first order moment for multiple daily streamflow processes and second-order moments for their multiple innovation time series, respectively. This study selected the upstream basin of Zarrineh Rood dam located in northwestern Iran for regional scale streamflow modeling. From the VAR and VAR–DVECH models, the following conclusions can be taken:

  • The twofold residuals of the linear VAR approach show the sufficiency of the fitted approach for each experiment, which it is verified with a multiple Ljung–Box test. However, the Portmanteau test confirms that the variance-covariance of the twofold residuals of the VAR model is not homoscedastic and exhibits time-varying features. Therefore, the VAR model is not efficient to illustrate the ARCH effect for daily streamflows.

  • To fully capture the effect of ARCH in the twofold residuals from the linear VAR approach, the VAR–DVECH error model is proposed and applied. The VAR–DVECH model is basically a combination of a VAR model which is used to model mean behavior and a DVECH model to model the ARCH effect in the twofold residuals from the VAR model. Therefore, with such a developed VAR–DVECH model, the multiple daily streamflow series is well-fitted.

  • The structure of conditional variance-covariance between twofold residuals of streamflow shows that long-term persistency is much higher than short-term persistency. Furthermore, the values of long-term persistency for upstream stations, which drain the smaller sub-basins, are less than those of the downstream locations. Moreover, there is a high level of temporal fluctuation in the conditional covariances between upstream and downstream stations changing for different times and experiments. However, the conditional covariance remains usually high for a short time and mostly at above the zero line for each experiment. This process is observed about the conditional correlation between twofold streamflows with a high level of relationship between twofold streamflows. Consequently, they usually keep near or below average amounts and suggest high time-variations and fluctuations during the time periods.

  • The DVECH model exhibits the advantage of capturing the conditional heteroscedasticity of the twofold residual time series obtained from the VAR approach. Moreover, in terms of the measures of evaluation criteria, the performance of the fitted models combined with DVECH approach is better than those models without that approach. The better performance of the MGARCH model may be due to the fact that the DVECH model considers the cross-product of the twofold residuals, which may lead to the stabilization of the variance and reduces the error of the model.

  • This study illustrates the main advantage of the DVECH model for multiple streamflow time series modeling. The DVECH model shows the time-varying association between innovations of twofold time series, herein the streamflow series of two different stations, for each time step. In other words, the conditional correlation coefficients are obtained between two different streamflow stations for each day. In addition, the DVECH model illustrates the association between the second order moment of twofold innovations of streamflows and their variation in time. The persistency of the second order moment of twofold innovations of streamflows and their association is also investigated by DVECH outputs.