Skip to main content
SpringerLink
Log in

A hidden Markov model for earthquake prediction

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

Abstract

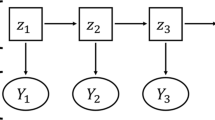
Earthquake occurrence is well-known to be associated with structural changes in underground dynamics, such as stress level and strength of electromagnetic signals. While the causation between earthquake occurrence and underground dynamics remains elusive, the modeling of changes in underground dynamics can provide insights on earthquake occurrence. However, underground dynamics are usually difficult to measure accurately or even unobservable. In order to model and examine the effect of the changes in unobservable underground dynamics on earthquake occurrence, we propose a novel model for earthquake prediction by introducing a latent Markov process to describe the underground dynamics. In particular, the model is capable of predicting the change-in-state of the hidden Markov chain, and thus can predict the time and magnitude of future earthquake occurrences simultaneously. Simulation studies and applications on a real earthquake dataset indicate that the proposed model successfully predicts future earthquake occurrences. Theoretical results, including the stationarity and ergodicity of the proposed model, as well as consistency and asymptotic normality of model parameter estimation, are provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • Adelfio G, Chiodi M (2015) Alternated estimation in semi-parametric space-time branching-type point processes with application to seismic catalogs. Stoch Environ Res Risk Assess 29:443450

    Google Scholar 

  • Bartolucci F, Farcomeni A (2009) A multivariate extension of the dynamic logit model for longitudinal data based on a latent Markov heterogeneity structure. J Am Stat Assoc 104:816–831

    Article  CAS  Google Scholar 

  • Bartolucci F, Farcomeni A (2015) A discrete time event-history approach to informative drop-out in mixed latent Markov models with covariates. Biometrics 71:80–89

    Article  Google Scholar 

  • Bartolucci F, Farcomeni A (2015a) Information matrix for hidden Markov models with covariates. Stat Comput 25:515–526

    Article  Google Scholar 

  • Bartolucci F, Farcomeni A, Pennoni F (2013) Latent Markov models for longitudinal data. Chapman & Hall, CRC Press, Boca Raton

    Google Scholar 

  • Baum LE, Petrie T, Soules G, Weiss N (1970) A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann Math Stat 41(1):164–171

    Article  Google Scholar 

  • Baum LE (1972) An equality and associated maximization technique in statistical estimation for probabilistic functions of Markov processes. Inequalities 3:1–8

    Google Scholar 

  • Bulla J, Berzel A (2008) Computational issues in parameter estimation for stationary hidden Markov models. Comput Stat 23(1):1–18

    Article  Google Scholar 

  • Cameletti M, De Rubies V, Ferrari C, Sbarra P, Tosi P (2016) An ordered probit model for seismic intensity data. Stoch Environ Res Risk Assess 1–10. doi:10.1007/s00477-016-1260-4

  • Cosentino P, Ficarra V, Luzio D (1977) Truncated exponential frequency-magnitude relationship in earthquake statistics. Bull Seismol Soc Am 67(6):1615–1623

    Google Scholar 

  • Davis PM, Jackson DD, Kagan YY (1989) The longer it has been since the last earthquake, the longer the expected time till the next? Bull Seismol Soc Am 79(5):1439–1456

    Google Scholar 

  • Ebel JE, Chambers DW, Kafka AL, Baglivo JA (2007) Non-Poissonian earthquake clustering and the hidden Markov model as bases for earthquake forecasting in California. Seismol Res Lett 78(1):57–65

    Article  Google Scholar 

  • Fierro R, Leiva V (2017) A stochastic methodology for risk assessment of a large earthquake when a long time has elapsed. Stoch Environ Res Risk Assess 1–10. doi:10.1007/s00477-016-1288-5

  • Finazzi F, Fassò A (2016) A statistical approach to crowdsourced smartphone-based earthquake early. Stoch Environ Res Risk Assess 1–10. doi:10.1007/s00477-016-1240-8

  • Huang Q, Ikeya M (1998) Seismic electromagnetic signals (SEMS) explained by a simulation experiment using electromagnetic waves. Phys Earth Planet Inter 109(3):107–114

    Article  CAS  Google Scholar 

  • Hughes JP, Guttorp P, Charles SP (1999) A non-homogeneous hidden Markov model for precipitation occurrence. J R Stat Soc Ser C (Appl Stat) 48(1):15–30

    Article  Google Scholar 

  • Hutton K, Woessner J, Hauksson E (2010) Earthquake monitoring in southern California for seventy-seven years (1932–2008). Bull Seismol Soc Am 100(2):423–446

    Article  Google Scholar 

  • Leroux BG (1992) Maximum-likelihood estimation for hidden Markov models. Stoch Process Appl 40(1):127–143

    Article  Google Scholar 

  • Leroux BG, Puterman ML (1992) Maximum-penalized-likelihood estimation for independent and Markov-dependent mixture models. Biometrics 48(2):545–558

    Article  CAS  Google Scholar 

  • Levinson SE, Rabiner LR, Sondhi MM (1983) An introduction to the application of the theory of probabilistic functions of a Markov process to automatic speech recognition. Bell Syst Tech J 62(4):1035–1074

    Article  Google Scholar 

  • Ogata Y (1981) On Lewis’ simulation method for point processes. IEEE Trans Inf Theory 27(1):23–31

    Article  Google Scholar 

  • Ogata Y (1988) Statistical models for earthquake occurrences and residual analysis for point processes. J Am Stat Assoc 83(401):9–27

    Article  Google Scholar 

  • Ogata Y (1998) Space-time point-process models for earthquake occurrences. Ann Inst Stat Math 50(2):379–402

    Article  Google Scholar 

  • Orfanogiannaki K, Karlis D, Papadopoulos GA (2010) Identifying seismicity levels via Poisson hidden Markov models. Pure Appl Geophys 167(8–9):919–931

    Article  Google Scholar 

  • Park SK, Johnston MJ, Madden TR, Morgan FD, Morrison HF (1993) Electromagnetic precursors to earthquakes in the ULF band: a review of observations and mechanisms. Rev Geophys 31(2):117–132

    Article  Google Scholar 

  • Reid HF (1910) The mechanics of the earthquake, vol. II of Lawson, A.C., chairman, The California earthquake of April 18, 1906: report of the State Earthquake Investigation Commission: Carnegie Institution of Washington Publication, p 192 (reprinted in 1969)

  • Seeber L, Armbruster JG (2000) Earthquakes as beacons of stress change. Nature 407(6800):69

    Article  CAS  Google Scholar 

  • Sornette D, Knopoff L (1997) The paradox of the expected time until the next earthquake. Bull Seismol Soc Am 87(4):789–798

    Google Scholar 

  • Team RC (2016) R: language and environment for statistical computing. R Foundation for Statistical Computing, 2005; Vienna, Austria

  • Telesca L, Giocoli A, Lapenna V, Stabile TA (2015) Robust identification of periodic behavior in the time dynamics of short seismic series: the case of seismicity induced by Pertusillo Lake, southern Italy. Stoch Environ Res Risk Assess 29:1437. doi:10.1007/s00477-014-0980-6

    Article  Google Scholar 

  • Utsu T (1961) A statistical study on the occurrence of aftershocks. Geophys Mag 30(4):521–605

    Google Scholar 

  • Viterbi AJ (1967) Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans Inf Theory 13(2):260–269

    Article  Google Scholar 

  • Welch LR (2003) Hidden Markov models and the Baum–Welch algorithm. IEEE Inf Theory Soc Newsl 53(4):10–13

    Google Scholar 

  • Zucchini W, MacDonald IL (2009) Hidden Markov models for time series: an introduction using R. CRC Press, Boca Raton

    Book  Google Scholar 

  • Zucchini W, Raubenheimer D, MacDonald IL (2008) Modeling time series of animal behavior by means of a latent-state model with feedback. Biometrics 64(3):807–815

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Medicine and Therapeutics, Chinese University of Hong Kong, Shatin, Hong Kong, China

    Cheuk Fung Yip

  2. Department of Statistics, Chinese University of Hong Kong, Shatin, Hong Kong, China

    Wai Leong Ng & Chun Yip Yau

Authors
  1. Cheuk Fung Yip
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wai Leong Ng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chun Yip Yau
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Cheuk Fung Yip.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 351 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yip, C.F., Ng, W.L. & Yau, C.Y. A hidden Markov model for earthquake prediction. Stoch Environ Res Risk Assess 32, 1415–1434 (2018). https://doi.org/10.1007/s00477-017-1457-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-017-1457-1

Keywords

Search

Navigation