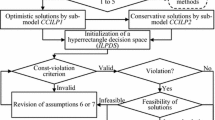
Abstract
Resources and environmental systems management (RESM) is challenged by the synchronic effects of interval uncertainties in the related practices. The synchronic interval uncertainties are misrepresented as random variables, fuzzy sets, or interval numbers in conventional RESM programming techniques including stochastic programming. This may lead to ineffectiveness of resources allocation, high costs of recourse measures, increased risks of unreasonable decisions, and decreased optimality of system profits. To fill the gap of few corresponding studies, a synchronic interval linear programming (SILP) method is proposed in this study. The proposition of interval sets and interval functions and coupling them with linear programming models lead to development of an SILP model for RESM. This enables incorporation of interval uncertainties in resource constraints and synchronic interval uncertainties in the programming objective into the optimization process. An analysis of the distribution-independent geometric properties of the feasible regions of SILP models results in proposition of constraint violation likelihoods. The tradeoff between system optimality and constraint violation is analyzed. The overall optimality of SILP systems under synchronic intervalness is quantified through proposition of integrally optimal solutions. Integration of these efforts leads to a violation-constrained interval integral method for optimization of RESM systems under synchronic interval uncertainties. Comparisons with selected existing methods reveal the effectiveness of SILP at eliminating negativity of synchronic intervalness, enabling risk management of and achieving overall optimality of RESM systems, and enhancing the reliability of optimization techniques for RESM problems. The exploited framework for analyzing synchronic interval uncertainties in RESM systems is helpful for addressing synchronisms of other uncertainties such as randomness or fuzziness and avoiding the resultant decision mistakes and disasters due to neglecting them.




Similar content being viewed by others
References
Ahmad A, El-Shafie A, Razali SFM, Mohamad ZS (2014) Reservoir optimization in water resources: a review. Water Resour Manage 28(11):3391–3405
Alefeld G, Mayer G (2000) Interval analysis: theory and applications. J Comput Appl Math 121(1):421–464
Anderson DR, Sweeney DJ, Williams TA, Camm JD (2015) An introduction to management science: quantitative approaches to decision making (Chapter 2). Cengage Learning, p 30
Banos R, Manzano-Agugliaro F, Montoya FG, Gil C, Alcayde A, Gómez J (2011) Optimization methods applied to renewable and sustainable energy: a review. Renew Sustain Energy Rev 15(4):1753–1766
Ben-Tal A, El Ghaoui L, Nemirovski A (2009) Robust optimization. Princeton Series in Applied Mathematics. Princeton University Press, Princeton, pp 9–16
Ben-Tal A, Nemirovski A (2002) Robust optimization–methodology and applications. Math Program 92(3):453–480
Bertsimas D, Brown DB, Caramanis C (2011) Theory and applications of robust optimization. SIAM Rev 53(3):464–501
Bertsimas D, Sim M (2004) The price of robustness. Oper Res 52(1):35–53
Birge JR, Louveaux F (2011) Introduction to stochastic programming. Springer, Berlin
Bitran GR (1980) Linear multiple objective problems with interval coefficients. Manage Sci 26(7):694–706
Chanas S, Kuchta D (1996) Multiobjetive programming in optimization of interval objective functions: a generalized approach. Eur J Oper Res 94:594–598
Charnes A, Cooper WW (1959) Chance-constrained programming. Manag Sci 6(1):73–79
Charnes A, Granot F, Phillips F (1977) An algorithm for solving interval linear programming problems. Oper Res 25:688–695
Cheng GH, Huang GH, Dong C (2015a) Synchronic interval Gaussian mixed-integer programming for air quality management. Sci Total Environ Elsevier 538(15):986–996
Cheng GH, Huang GH, Dong C (2015b) Interval recourse linear programming for resources and environmental systems management under uncertainty. J Environ Inf (International Society of Environmental Information Sciences). Online express
Cheng GH, Huang GH, Dong C (2017) Convex contractive interval linear programming for resources and environmental systems management. Stoch Env Res Risk Assess 31(1):205–224
Cheng GH, Huang GH, Li YP, Cao MF, Fan YR (2009) Planning of municipal solid waste management systems under dual uncertainties: a hybrid interval stochastic programming approach. Stoch Environ Res Risk Assess 23(6):707–720
Chinneck JW, Ramadan K (2000) Linear programming with interval coefficients. J Oper Res Soc 51(2):209–220
Dantzig GB (1947) Maximization of a linear function of variables subject to linear inequalities. Activity Analysis of Production and Allocation, New York-London 339–347
Dantzig GB (1963) Linear programming and extensions. Princeton University Press, Princeton
Dantzig GB, Wolfe P (1960) The decomposition principle for linear programs. Oper Res 8:101–111
Dong C, Huang GH, Cai YP, Li W, Cheng GH (2014a) Fuzzy interval programming for energy and environmental systems management under constraint-violation and energy-substitution effects: a case study for the city of Beijing. Energy Econ 11(2014):46. doi:10.1016/j.eneco.2014.09.024
Dong C, Huang GH, Cai YP, Liu Y (2012) An inexact optimization modeling approach for supporting energy systems planning and air pollution mitigation in Beijing City. Energy (Elsevier) 37(1):673–688
Dong C, Huang GH, Cai YP, Liu Y (2013a) Robust planning of energy management systems with environmental and constraint-conservative considerations under multiple uncertainties. Energy Convers Manag 65:471–486. doi:10.1016/j.enconman.2012.09.001
Dong C, Huang GH, Cai YP, Xu Y (2011) An interval-parameter minimax regret programming approach for power management systems planning under uncertainty. Appl Energy 88(8–88):2835–2845. doi:10.1016/j.apenergy.2011.01.056
Dong C, Huang GH, Cai YP, Yue WC, Rong QQ (2014b) An interval-parameter fuzzy linear programming approach for accounting and planning of energy-environmental management systems. J Environ Account Manag 2(1):13–29. doi:10.5890/JEAM.2014.03.002
Dong C, Huang GH, Tan Q (2015) A robust optimization modelling approach for managing water and farmland use between anthropogenic modification and ecosystems protection under uncertainties. Ecol Eng 76:95–109. doi:10.1016/j.ecoleng.2014.04.003
Dong C, Huang GH, Tan Q, Cai YP (2014c) Coupled planning of water resources and agricultural land-use based on an inexact-stochastic programming model. Front Earth Sci. doi:10.1007/s11707-013-0388-5
Dong C, Tan Q, Huang GH, Cai YP (2013b) A dual-inexact fuzzy stochastic model for water resources management and non-point source pollution mitigation under multiple uncertainties. Hydrol Earth Syst Sci. doi:10.5194/hessd-11-987-2014
Gabrel V, Murat C, Thiele A (2014) Recent advances in robust optimization: an overview. Eur J Oper Res 235(3):471–483
Grinstead C, Snell JL (1997) Introduction to probability. American Mathematical Society, Providence, pp 10–11
Hladık M (2012) Interval linear programming: a survey. In: Mann ZA (ed) Linear Programming-New frontiers in theory and applications, ch 2. Nova Science Publishers, New York, pp 85–120
Huang GH, Baetz BW, Patry GG (1992) An interval linear programming approach for municipal solid waste management planning under uncertainty. Civ Eng Syst 9:319–335
Inuiguchi M (1993) Fuzzy mathematical programming. Fuzzy Operations Research, Nikkan Kougyou Sinbunsha, Tokyo, pp 41–90
Inuiguchi M, Ramík J (2000) Possibilistic linear programming: a brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Sets Syst 111(1):3–28
Inuiguchi M, Ramik J, Tanino T, Vlach M (2003) Satisficing solutions and duality in interval and fuzzy linear programming. Fuzzy Sets Syst 135:151–177
Inuiguchi M, Sakawa M (1995) Minimax regret solution to linear programming problems with an interval objective function. Eur J Oper Res 86:526–536
Inuiguchi M, Sakawa M (1997) An achievement rate approach to linear programming problems with an interval objective function. J Oper Res Soc 48(1):25–33
Ishibuchi H, Tanaka H (1990) Multiobjective programming in optimization of the interval objective function. Eur J Oper Res 48:219–225
Ivanov D, Dolgui A, Sokolov B (2012) Applicability of optimal control theory to adaptive supply chain planning and scheduling. Annu Rev Control 36(1):73–84
Jamison KD, Lodwick WA (2001) Fuzzy linear programming using a penalty method. Fuzzy Sets Syst 119:97–110
Kahraman C (2008) Fuzzy multi-criteria decision making: theory and applications with recent developments. Springer, Berlin
Kantorovich LV (1940) A new method of solving some classes of extremal problems. Doklady Akad Sci USSR 28:211–214
Klaus M, Albert T (1995) Monte Carlo sampling of solutions to inverse problems. J Geophys Res 100(B7):12431–12447
Lee JH (2011) Model predictive control: review of the three decades of development. Int J Control Autom Syst 9(3):415–424
Levin VI (1994) Boolean linear programming with interval coefficients. Autom Remote Control 55:1019–1028
Lin MH, Tsai JF, Yu CS (2012) A review of deterministic optimization methods in engineering and management. Math Probl Eng 2012:1–15
Luhandjula MK (2014) Fuzzy optimization: milestones and perspectives. Fuzzy Sets Syst 274:4–11
Maqsood I, Huang GH (2003) A two-stage interval-stochastic programming model for waste management under uncertainty. J Air Waste Manag Assoc Air Waste Manag Assoc 53(5):540–552
Mérel P, Howitt R (2014) Theory and application of positive mathematical programming in agriculture and the environment. Annu Rev Resour Econ 6(1):451–470
Metropolis N, Ulam S (1949) The monte carlo method. J Am Stat Assoc 44(247):335–341
Moore RE (1979) Method and application of interval analysis. SIAM, Philadelphia
Peter K, Mayer J (1976) Stochastic linear programming. Springer, Berlin
Prékopa A (1990) Sharp bound on probabilities using linear programming. Oper Res 38:227–239
Psacharopoulos G (2014) Economics of education: research and studies. Elsevier, Amsterdam
Quaeghebeur E, Shariatmadar K, De Cooman G (2012) Constrained optimization problems under uncertainty with coherent lower previsions. Fuzzy Sets Syst 206:74–88
Rommelfanger H, Hanuscheck R, Wolf J (1989) Linear programming with fuzzy objectives. Fuzzy Sets Syst 29:31–48
Ruszczynski A, Shapiro A (2003) Stochastic programming. Handbooks in operations research and management science. Elsevier, Amsterdam
Sengupta A, Pal TK (2000) On comparing interval sets. Eur J Oper Res 127:28–43
Sengupta A, Pal TK, Chakraborty D (2001) Interpretation of inequality constraints involving interval coefficients and a solution to interval linear programming. Fuzzy Sets Syst 119:129–138
Soyster AL (1973) Technical note: convex programming with set-inclusive constraints and applications to inexact linear programming. Oper Res 21(5):1154–1157
Steuer RE (1981) Algorithms for linear programming problems with interval objective function coefficients. Math Oper Res 6:33–348
Tang SC, Zhou S (2012) Research advances in environmentally and socially sustainable operations. Eur J Oper Res 223(3):585–594
Tong SC (1994) Interval set and fuzzy number linear programming. Fuzzy Sets Syst 66:301–306
Acknowledgements
This research was supported by the National Key Research and Development Plan (2016YFC0502800, 2016YFA0601502), the Natural Sciences Foundation (51520105013, 51679087), the 111 Project (B14008) and the Natural Science and Engineering Research Council of Canada. We are very grateful to the editor and two anonymous peer reviewers who provided many constructive comments on how to improve our manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Lemma 1
Solutions under the conservative boundary are absolutely feasible, and that out of the optimistic boundary are infeasible.
Proof
Let R − = {X | A + X ≤ b − and X ≥ 0}, R + = {X | A − X ≤ b + and X ≥ 0}, and R(b, A) = {X | AX ≤ b; A − ≤ A ≤ A +; X ≥ 0; b − ≤ b ≤ b +; (b, A) ≠ (b −, A +) or (b +, A −); (b + − b −) + ∑ j=1,2,…,n (a + j − a − j ) > 0}. The lemma is equivalent with R − ⊂ R(b, A) ⊂ R +. Let X = (x 1,x 2,…,x n ) be any element in R −, and A be a real vector satisfying A − ≤ A ≤ A +. From definitions of R −, we have A + X ≤ b −, X ≥ 0, and AX ≤ A + X. Namely, AX ≤ A + X ≤ b − ≤ b where b − ≤ b ≤ b +. Thus, X ∈ R(b, A), i.e. R −⊆ R(b, A). Since (b, A) ≠ (b −, A +), R − absolutely belongs to R(b, A). Let X * = (x *1 , x *2 , …, x * n ) be any vector in R(b, A) and satisfy X *∉ R −. Similarly, we have X * ∈ R +, i.e. R(b, A) ⊆ R +. Accordingly, R(b, A) absolutely belongs to R + because (b, A) ≠ (b +, A −).□
Proposition 1
Let X be any solution in R s where R s = {X | X ≥ 0; A + X > b −; A − X ≤ b +; (b + − b −) + ∑ j=1,2,…,n (a + j − a − j ) > 0}. We have d X T + d X L > 0.
Proof
For any X ∈ R s, we have X ≥ 0, A + X > b −, A − X ≤ b +, and (b + − b −) + ∑ j=1,2,…,n (a + j − a − j ) > 0. Since A + X − b − > 0, b + − A − X ≥ 0, (A +)(A +)T > 0 and (A −)(A −)T > 0, we have d X T ≥ 0 and d X L ≥ 0. Accordingly, we have d X T + d X L ≥ 0. If d X T = 0 and d X L = 0, we have (A + X − b −)/((A +)(A +)T) = 0 and (b + − A − X) / ((A −)(A −)T) = 0, i.e. A + X = b − and A − X = b +. Equivalently, ∑ j=1,2,…,n (a + j ·x j ) = b −, ∑ j=1,2,…,n (a − j ·x j ) = b +, and ∑ j=1,2,…,n (a + j − a − j )·x j = b − − b +. Since ∑ j=1,2,…,n (a + j − a − j )·x j ≥ 0 and b − − b + ≤ 0, equality ∑ j=1,2,…,n (a + j − a − j )·x j = b − − b + holds for any solution of non-negative decision variables x j (j = 1, 2, …, n) if and only if b + = b − and a + j = a − j for any j ∈ {1, 2, …, n}. As a result, (b + − b −) + ∑ j=1,2,…,n (a + j − a − j ) = 0, which contradicts with the given condition (b + − b −) + ∑ j=1,2,…,n (a + j − a − j ) > 0. Thus, it does not hold that d X T = d X L = 0.□
Theorem 1
For any i ∈ {1, 2, …, t}, the ith constraint in SILP model (1) is equivalent to inequality (2).
Proof
From formulations of CVL i , we have inequality CVL i ≤ CVL imax is equivalent with [(A + i X − b − i )/((A + i )(A + i )T)]/{[(A i + X − b − i )/((A + i )(A + i )T)] + [(b i + − A − i X)/((A − i )(A i −)T)]} ≤ CVL imax. Since X ∈ R s, we have A + X > b −, A − X ≤ b +, and (b + − b −) + ∑ j=1,2,…,n (a + j − a − j ) > 0. Therefore, [(A + i )(A + i )T(b i + − A − i X) + (A − i )(A i −)T(A + i X − b − i )] > 0. Besides, it holds for any i ∈ {1, 2, …, t} that (A − i )(A i −)T ≥ 0 and (A + i )(A + i )T ≥ 0. Thus, we have inequality [(A i + X − b − i )/((A + i )(A + i )T)]/{[(A i + X − b − i )/((A + i )(A + i )T)] + [(b i + − A − i X)/((A − i )(A i −)T)]} ≤ CVL imax is equivalent to [(A + i X − b − i ) / ((A + i )(A i +)T)] ≤ (CVL imax){[(A + i X − b − i ) / ((A + i )(A + i )T)] + [(b i + − A − i X) / ((A − i )(A i −)T)]}, (1 − CVL imax)(A + i X − b − i )((A − i )(A i −)T) ≤ (CVL imax)(b + i − A − i X)((A + i )(A i +)T), and then [(1 − CVL imax)(A − i )(A i −)T A + i + (CVL imax)(A + i )(A i +)T A − i ]X ≤ (CVL imax)(A + i ) (A + i )T b i + + (1 − CVL imax)(A − i )(A − i )T b − i .□
Proposition 2
For any i ∈ {1, 2, …, t}, assume X ∈ R s and CVL imax1 and CVL imax2 are any two values of CVL imax. If CVL imax1 < CVL imax2 and A i (CVL imax1)X ≤ b i (CVL imax1), then A i (CVL imax2)X ≤ b i (CVL imax2).
Proof
Let X be any vector in {X | X ∈ R s; A i (CVL imax1)X ≤ b i (CVL imax1)}. Then X satisfies X ∈ R s and A i (CVL imax1)X ≤ b i (CVL imax1). From Theorem 1, we have inequality A i (CVL imax1)X ≤ b i (CVL imax1) is equivalent with [(A + i X − b − i )/((A + i )(A + i )T)]/{[(A + i X − b − i )/((A + i )(A + i )T)] + [(b + i − A − i X)/((A − i )(A − i )T)]} ≤ CVL imax1. Since CVL imax1 < CVL imax2, so [(A + i X − b − i )/((A + i )(A + i )T)]/{[(A + i X − b − i )/((A + i )(A + i )T)] + [(b + i − A − i X)/((A − i )(A − i )T)]} < CVL imax2. Namely, X belongs to {X | X ∈ R s and A i (CVL imax2)X ≤ b i (CVL imax2)}. No element in {X | X ∈ R s and A i (CVL imax1)X ≤ b i (CVL imax1)} can satisfy A i (CVL imax2)X = b i (CVL imax2), because CVL imax1 < CVL imax2. Therefore, {X | X ∈ R s and A i (CVL imax1)X ≤ b i (CVL imax1)} absolutely belongs to {X | X ∈ R s and A i (CVL imax2)X ≤ b i (CVL imax2)}.□
Remark 1
For any CVL imax ∈ [0, 1] and any i ∈ {1, 2, …, t}, L ij (CVL imax) ∈ [a − ij , a + ij ] and R i (CVL imax) ∈ [b − i , b + i ] where L ij (CVL imax) = [(1 − CVL imax)·a + ij ·(A − i )(A i −)T + (CVL imax)·a − ij ·(A + i )(A i +)T]/[(1 − CVL imax)·(A − i )(A i −)T + (CVL imax)·(A + i )(A i +)T] and R i (CVL imax) = [(CVL imax)·b + i ·(A + i )(A i +)T + (1 − CVL imax)·b − i ·(A − i )(A i −)T]/[(1 − CVL imax)·(A − i )(A i −)T + (CVL imax)·(A + i )(A i +)T].
Proof
Based on formulations of L ij (CVL imax) and R i (CVL imax), it is equivalent to prove [(1 − CVL imax)·a + ij ·(A − i )(A i −)T + (CVL imax)·a − ij ·(A + i )(A i +)T] ≥ [(1 − CVL imax)·(A − i )(A i −)T + (CVL imax)·(A + i ) (A i +)T]·a − ij , [(1 − CVL imax)·a + ij ·(A − i )(A i −)T + (CVL imax)·a − ij ·(A + i )(A i +)T] ≤ [(1 − CVL imax)·(A − i )(A i −)T + (CVL imax)·(A + i ) (A i +)T]·a + ij , [(CVL imax)·b + i ·(A i +)(A i +)T + (1 − CVL imax)·b − i ·(A i −)(A i −)T] ≥ [(1 − CVL imax)·(A − i )(A i −)T + (CVL imax)·(A + i )(A i +)T]·b − i , and [(CVL imax)·b + i ·(A i +)(A i +)T + (1 − CVL imax)·b − i ·(A i −) (A − i )T] ≤ [(1 − CVL imax)·(A − i )(A i −)T + (CVL imax)·(A + i )(A i +)T]·b i +. Namely, [(1 − CVL imax)·a + ij ·(A − i )(A − i )T] ≥ [(1 − CVL imax)·(A − i )(A i −)T]·a − ij , [(CVL imax)·a − ij ·(A + i )(A i +)T] ≤ [(CVL imax)·(A + i )(A i +)T]·a + ij , [(CVL imax)·b + i ·(A i +)(A i +)T] ≥ [(CVL imax)·(A + i )(A i +)T]·b − i , and [(1 − CVL imax)·b − i ·(A i −)(A i −)T] ≤ [(1 − CVL imax)·(A − i )(A i −)T]·b + i . These inequalities hold because, for any i ∈ {1, 2, …, t} and any j ∈ {1, 2, …, n}, we have 1 − CVL imax ≥ 0, CVL imax ≥ 0, (A − i )(A i −)T ≥ 0, (A + i )(A i +)T ≥ 0, a + ij ≥ a − ij and b + i ≥ b − i .□
Theorem 2
DCVL(CVL imax) < DCVL(CVL imax) if CVL imax1 < CVL imax2 where CVL imax1 and CVL imax2 are two levels of CVL imax.
Proof
Due to the formulation of DCVL(CVL imax), it is sufficient to prove that both F ij (L ij (CVL imax)) and G i (R i (CVL imax)) are monotonically decreasing with CVL imax for any i ∈ {1, 2, …, t} and j ∈ {1, 2, …, n}. It is equivalent to prove that a) L ij (CVL imax1) ≥ L ij (CVL imax2) and b) R i (CVL imax1) ≤ R i (CVL imax2), since both F ij (·) and G i (·) are monotonically increasing functions.
(a). Since CVL imax1 ≤ CVL imax2 and a − ij ≤ a + ij , we have (CVL imax1−CVL imax2)·(a − ij − a + ij ) ≥ 0. Because (A + i )(A i +)T·(A − i )(A i −)T > 0, we have (CVL imax1)·(1 − CVL imax2)·a − ij + (1 − CVL imax1)·(CVL imax2)·a + ij ≥ (CVL imax2)·(1 − CVL imax1)·a − ij + (1 − CVL imax2)·(CVL imax1)·a + ij . Equivalently, we have (1 − CVL imax1)·(1 − CVL imax2)·a + ij ·(A − i )(A − i )T·(A i −)(A i −)T + [(CVL imax1)·(1 − CVL imax2)·a − ij + (1 − CVL imax1)·(CVL imax2)·a + ij ]·(A + i ) (A i +)T·(A − i )(A i −)T + (CVL imax1)·(CVL imax2)·a − ij ·(A + i )(A i +)T·(A i +)(A i +)T ≥ (1 − CVL imax1)·(1 − CVL imax2)·a + ij ·(A − i )(A i −)T·(A i −)(A i −)T + [(1 − CVL imax1)·(CVL imax2)·a − ij + (CVL imax1)·(1 − CVL imax2)·a + ij ]·(A + i ) (A i +)T·(A − i )(A i −)T + (CVL imax1)·(CVL imax2)·a − ij ·(A + i )(A i +)T·(A i +)(A i +)T, and furthermore (1 − CVL imax1)·a + ij · (A − i )(A − i )T·(1 − CVL imax2)·(A − i )(A i −)T + (CVL imax1)·a − ij ·(A + i )(A i +)T·(1 − CVL imax2)·(A − i )(A − i )T + (1 − CVL imax1)·a + ij ·(A i −)(A i −)T·(CVL imax2)·(A + i )(A + i )T + (CVL imax1)·a − ij ·(A + i ) (A i +)T·(CVL imax2)·(A + i )(A i +)T ≥ (1 − CVL imax2)·a + ij ·(A − i )(A i −)T·(1 − CVL imax1)·(A − i )(A i −)T + (CVL imax2)·a − ij ·(A + i )(A i +)T·(1 − CVL imax1)·(A − i ) (A i −)T + (1 − CVL imax2)·a + ij ·(A i −)(A i −)T·(CVL imax1)·(A + i ) (A i +)T + (CVL imax2)·a − ij ·(A + i )(A i +)T·(CVL imax1)·(A + i ) (A i +)T. Since [(1 − CVL imax)·(A − i )(A i −)T + (CVL imax)·(A + i )(A i +)T] ≥ 0 for any CVL imax ∈ [0, 1] and any i ∈ {1, 2, …, t}, we have [(1 − CVL imax1)·a + ij ·(A − i )(A i −)T + (CVL imax1)·a − ij ·(A + i )(A i +)T]·[(1 − CVL imax2)·(A − i ) (A i −)T + (CVL imax2)·(A + i ) (A i +)T] ≥ [(1 − CVL imax2)·a + ij ·(A − i )(A i −)T + (CVL imax2)·a − ij ·(A + i )(A i +)T]·[(1 − CVL imax1)·(A − i )(A i −)T + (CVL imax1)·(A + i )(A i +)T]. Thus, [(1 − CVL imax1)·a + ij ·(A − i )(A i −)T + (CVL imax1)·a − ij ·(A + i ) (A i +)T]/[(1 − CVL imax1)·(A − i )(A i −)T + (CVL imax1)·(A + i )(A i +)T] ≥ [(1 − CVL imax2)·a + ij ·(A − i )(A i −)T + (CVL imax2)·a − ij ·(A + i ) (A i +)T]/[(1 − CVL imax2)·(A − i )(A i −)T + (CVL imax2)·(A + i )(A i +)T]. It is equivalent to L ij (CVL imax1) ≥ L ij (CVL imax2) from the formulation of L ij (CVL imax).□
(b). From the formulation of R i (CVL imax), we are going to prove [(CVL imax1)·b + i ·(A + i )(A i +)T + (1 − CVL imax1)·b − i ·(A i −)(A i −)T]/[(1 − CVL imax1)·(A − i )(A i −)T + (CVL imax1)·(A + i )(A i +)T] ≤ [(CVL imax2)·b + i ·(A i +) (A i +)T + (1 − CVL imax2)·b − i ·(A i −)(A i −)T]/[(1 − CVL imax2)·(A − i )(A i −)T + (CVL imax2)·(A + i )(A i +)T]. That is, [(CVL imax1)·b + i ·(A i +)(A i +)T + (1 − CVL imax1)·b − i ·(A i −)(A i −)T]·[(1 − CVL imax2)·(A − i )(A i −)T + (CVL imax2)·(A + i ) (A + i )T] ≤ [(CVL imax2)·b + i ·(A i +)(A i +)T + (1 − CVL imax2)·b − i ·(A i −)(A − i )T]·[(1 − CVL imax1)·(A − i )(A i −)T + (CVL imax1)·(A + i )(A + i )T], or (CVL imax1)·b + i ·(A i +)(A i +)T·(1 − CVL imax2)·(A − i )(A − i )T + (1 − CVL imax1)·b − i ·(A i −) (A − i )T·(1 − CVL imax2)·(A − i )(A i −)T + (CVL imax1)·b + i ·(A i +)(A i +)T·(CVL imax2)·(A + i )(A i +)T + (1 − CVL imax1)·b − i ·(A i −) (A i −)T·(CVL imax2)·(A + i )(A i +)T ≤ [(CVL imax2)·b + i ·(A i +)(A i +)T·(1 − CVL imax1)·(A − i )(A i −)T + (1 − CVL imax2)·b − i ·(A i −)(A i −)T·(1 − CVL imax1)·(A − i )(A i −)T + (CVL imax2)·b + i ·(A + i )(A i +)T·(CVL imax1)·(A + i ) (A i +)T + (1 − CVL imax2)·b − i ·(A − i )(A i −)T·(CVL imax1)·(A + i )(A + i )T. It is equivalent to [(CVL imax1)·(1 − CVL imax2)·b + i + (1 − CVL imax1)·b − i ·(CVL imax2)]·(A + i )(A + i )T·(A − i )(A − i )T + (1 − CVL imax1)·(1 − CVL imax2)·b − i ·(A − i )(A − i )T·(A − i )(A − i )T + (CVL imax1)·(CVL imax2)·b + i ·(A + i )(A + i )T·(A + i )(A + i )T ≤ [(1 − CVL imax1)·(CVL imax2)·b + i + (CVL imax1)·(1 − CVL imax2)·b − i ]·(A + i )(A i +)T·(A − i )(A i −)T + (1 − CVL imax1)·(1 − CVL imax2)·b − i ·(A − i )(A − i )T·(A − i )(A i −)T + (CVL imax1)·(CVL imax2)·b + i ·(A + i )(A i +)T·(A + i )(A i +)T. Since CVL imax1 ≤ CVL imax2 and b − i ≤ b + i , we have [(CVL imax1)·(1 − CVL imax2)·b + i + (1 − CVL imax1)·b − i ·(CVL imax2)] − [(1 − CVL imax1)·(CVL imax2)·b + i + (CVL imax1)·(1 − CVL imax2)·b − i ] = (CVL imax1−CVL imax2)·(b + i − b − i ) and (CVL imax1−CVL imax2)·(b + i − b − i ) ≤ 0. At the meantime, (A + i )(A + i )T·(A − i )(A − i )T ≥ 0. Thus, we have R i (CVL imax1) ≤ R i (CVL imax2).□
Theorem 3
If the necessarily optimal solution exists for SILP-2 model (3), the integrally optimal solution equals to the necessarily optimal solution.
Proof
Let X opt = (x 1opt, x 2opt, …, x nopt) be the integrally optimal solution of model (3). From Definition 6, we have \(\int \ldots \int \left\{ {\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{j} } \right]} } \right\}d\left( {d_{1} } \right) \ldots d\left( {d_{r} } \right)\) is maximized when X = X opt. Namely, there does not exist another feasible solution X ′ = (x ′1 , x ′2 , …, x ′ n ) such that \(\int \ldots \int \left\{ {\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{j}^{\prime } } \right]} } \right\}d\left( {d_{1} } \right) \ldots d\left( {d_{r} } \right) \, \quad > \, \int \ldots \int \left\{ {\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{{j{\text{opt}}}} } \right]} } \right\}d\left( {d_{1} } \right) \ldots d\left( {d_{r} } \right)\). Assume X opt is not the necessarily optimal solution that exists for SILP-2 model (3). From the definition of necessarily optimal solution, there must exist another vector of feasible solutions, assumed as X ″ = (x ″1 , x ″2 , …, x ″ n ), such that \(\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{j}^{\prime \prime } } \right]} \, \ge \, \sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{{j{\text{opt}}}} } \right]}\) for all combinations of d k ∈ [d − k , d + k ] (k = 1, 2, …, r) and \(\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{j}^{\prime \prime } } \right]} > \sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{{j{\text{opt}}}} } \right]}\) for at least one combination of d k ∈ [d − k , d + k ] (k = 1, 2, …, r). Thus, we have \(\int \ldots \int \left\{ {\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{j}^{\prime \prime } } \right]} } \right\}d\left( {d_{1} } \right) \ldots d\left( {d_{r} } \right) > \int \ldots \int \left\{ {\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{{j{\text{opt}}}} } \right]} } \right\}d\left( {d_{1} } \right) \ldots d\left( {d_{r} } \right)\). This is contradictory to the maximization of \(\int \ldots \int \left\{ {\sum\nolimits_{j = 1}^{n} {\left[ {\left[ {g_{j} \left( {d_{1} ,d_{2} , \ldots ,d_{r} } \right) \, + h_{j} } \right]x_{{j{\text{opt}}}} } \right]} } \right\}d\left( {d_{1} } \right) \ldots d\left( {d_{r} } \right)\). Therefore, the integrally optimal solution is also the necessarily optimal solution.□
Rights and permissions
About this article
Cite this article
Cheng, G., Huang, G., Dong, C. et al. Resources and environmental systems management under synchronic interval uncertainties. Stoch Environ Res Risk Assess 32, 435–456 (2018). https://doi.org/10.1007/s00477-017-1445-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-017-1445-5