Discrete convolution and FFT modified with double influence-coefficient superpositions (DCSS–FFT) for contact of nominally flat heterogeneous materials involving elastoplasticity

Abstract

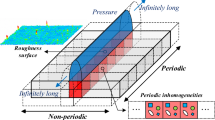
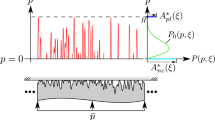
The contact of nominally flat surfaces can be treated as a bilateral periodic contact problem considering the stochastic surface similarity to the asperity distribution in a representative region. This similarity treatment method can be extended to material inhomogeneities. A novel numerical model for simulating the elastoplastic contact between nominally flat surfaces of materials containing inhomogeneities or coatings is developed via extending the concept of the discrete convolution and FFT (DC–FFT) algorithm with double superpositions of influence coefficients, which is named the DCSS–FFT algorithm. Several cases are analyzed with this new algorithm to examine its convenience, efficiency, and accuracy in dealing with complicated nominally flat–flat contact problems. The effects of surface roughness and material inhomogeneity are explored, and the mechanisms of contact surface failure are discussed.

Appendix

1.1 ICs for surface deformation of homogeneous materials based on the zero-order approximation

When a uniform pressure, p, is applied on the surface of an elastic half-space in a rectangular area of $2a_{1} \times 2a_{2}$, the normal surface displacement at point (x, y) can be obtained from the following expression [41].

$$ \begin{aligned} \frac{\pi E}{{1 - \upsilon^{2} }} \cdot \frac{{u_{Z} }}{p} & = \left( {x + a_{1} } \right)\left[ {\frac{{\left( {y + a_{2} } \right) + \sqrt {\left( {y + a_{2} } \right)^{2} + \left( {x + a_{1} } \right)^{2} } }}{{\left( {y - a_{2} } \right) + \sqrt {\left( {y - a_{2} } \right)^{2} + \left( {x + a_{1} } \right)^{2} } }}} \right] \\ & \quad + \,\left( {y + a_{2} } \right)\left[ {\frac{{\left( {x + a_{1} } \right) + \sqrt {\left( {y + a_{2} } \right)^{2} + \left( {x + a_{1} } \right)^{2} } }}{{\left( {x - a_{1} } \right) + \sqrt {\left( {y + a_{2} } \right)^{2} + \left( {x - a_{1} } \right)^{2} } }}} \right] \\ & \quad + \,\left( {x - a_{1} } \right)\left[ {\frac{{\left( {y - a_{2} } \right) + \sqrt {\left( {y - a_{2} } \right)^{2} + \left( {x - a_{1} } \right)^{2} } }}{{\left( {y + a_{2} } \right) + \sqrt {\left( {y + a_{2} } \right)^{2} + \left( {x - a_{1} } \right)^{2} } }}} \right] \\ & \quad + \,\left( {y - a_{2} } \right)\left[ {\frac{{\left( {x - a_{1} } \right) + \sqrt {\left( {y - a_{2} } \right)^{2} + \left( {x - a_{1} } \right)^{2} } }}{{\left( {x + a_{1} } \right) + \sqrt {\left( {y - a_{2} } \right)^{2} + \left( {x + a_{1} } \right)^{2} } }}} \right] \\ \end{aligned} $$

(27)

The general relationships between pressure and vertical surface deformation are defined as the form of discrete convolution:

$$ u_{z[\alpha ,\beta ]} = \sum\limits_{\xi = 0}^{Nx - 1} {\sum\limits_{\eta = 0}^{Ny - 1} {D_{[\alpha - \xi ,\beta - \eta ]} p_{[\xi ,\eta ]} } } $$

(28)

where $Nx$. and $Ny$ are the total numbers of elements in the target domain along the $x$ and $y$ direction, and $\alpha$, $\beta$, $\xi ,$ and $\eta$ are the element indices. According to Eq. (27), the ICs can be expressed as:

$$ \begin{aligned} D_{{\left[ {\alpha - \xi ,\beta - \eta } \right]}} & = \frac{{1 - \upsilon^{2} }}{\pi E}\left\{ {\left( {x_{\alpha } - x_{\xi } + a_{1} } \right)\left[ {\frac{{\left( {y_{\beta } - y_{\eta } + a_{2} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } + a_{1} } \right)^{2} } }}{{\left( {y_{\beta } - y_{\eta } - a_{2} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } + a_{1} } \right)^{2} } }}} \right]} \right. \\ & \quad + \,\left( {y_{\beta } - y_{\eta } + a_{2} } \right)\left[ {\frac{{\left( {x_{\alpha } - x_{\xi } + a_{1} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } + a_{1} } \right)^{2} } }}{{\left( {x_{\alpha } - x_{\xi } - a_{1} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } - a_{1} } \right)^{2} } }}} \right] \\ & \quad + \,\left( {x_{\alpha } - x_{\xi } - a_{1} } \right)\left[ {\frac{{\left( {y_{\beta } - y_{\eta } - a_{2} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } - a_{1} } \right)^{2} } }}{{\left( {y_{\beta } - y_{\eta } + a_{2} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } - a_{1} } \right)^{2} } }}} \right] \\ & \quad \left. { + \,\left( {y_{\beta } - y_{\eta } - a_{2} } \right)\left[ {\frac{{\left( {x_{\alpha } - x_{\xi } - a_{1} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } - a_{1} } \right)^{2} } }}{{\left( {x_{\alpha } - x_{\xi } + a_{1} } \right) + \sqrt {\left( {y_{\beta } - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha } - x_{\xi } + a_{1} } \right)^{2} } }}} \right]} \right\} \\ \end{aligned} $$

(29)

When using the ICs-superposition with the DCSS–FFT algorithm,

$$ D_{{\left[ {\alpha ,\beta } \right]}}^{sum} = \sum\limits_{t = - n}^{n} {\sum\limits_{r = - m}^{m} {D_{{\left[ {\alpha + tNx,\beta + rNy} \right]}}^{{\left( {0,0} \right)}} } } $$

(30)

Then the once forever ICs-superposition becomes:

$$ \begin{aligned} D_{{\left[ {\alpha - \xi ,\beta - \eta } \right]}}^{sum} & = \frac{{1 - \upsilon^{2} }}{\pi E}\sum\limits_{t = - n}^{n} {\sum\limits_{r = - m}^{m} {\left\{ {\left( {x_{\alpha + tNx} - x_{\xi } + a_{1} } \right)\left[ {\frac{{\left( {y_{\beta + rNy} - y_{\eta } + a_{2} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } + a_{1} } \right)^{2} } }}{{\left( {y_{\beta + rNy} - y_{\eta } - a_{2} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } + a_{1} } \right)^{2} } }}} \right]} \right.} } \\ & \quad + \,\left( {y_{\beta + rNy} - y_{\eta } + a_{2} } \right)\left[ {\frac{{\left( {x_{\alpha + tNx} - x_{\xi } + a_{1} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } + a_{1} } \right)^{2} } }}{{\left( {x_{\alpha + tNx} - x_{\xi } - a_{1} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } - a_{1} } \right)^{2} } }}} \right] \\ & \quad + \,\left( {x_{\alpha + tNx} - x_{\xi } - a_{1} } \right)\left[ {\frac{{\left( {y_{\beta + rNy} - y_{\eta } - a_{2} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } - a_{1} } \right)^{2} } }}{{\left( {y_{\beta + rNy} - y_{\eta } + a_{2} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } + a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } - a_{1} } \right)^{2} } }}} \right] \\ & \quad \left. { + \,\left( {y_{\beta + rNy} - y_{\eta } - a_{2} } \right)\left[ {\frac{{\left( {x_{\alpha + tNx} - x_{\xi } - a_{1} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } - a_{1} } \right)^{2} } }}{{\left( {x_{\alpha + tNx} - x_{\xi } + a_{1} } \right) + \sqrt {\left( {y_{\beta + rNy} - y_{\eta } - a_{2} } \right)^{2} + \left( {x_{\alpha + tNx} - x_{\xi } + a_{1} } \right)^{2} } }}} \right]} \right\} \\ \end{aligned} $$

(31)

This only need to be calculated once for all.