Abstract
Many engineering scenarios involve contact between beam structures or, eventually, self-contact. Specifically when dealing with a beam submitted to large torsion loads and considering large displacements and rotations, it is possible to occur self-contact. Beams with low bending stiffness loaded with large torsion can present a loop, followed by self-contact and sometimes a snarl formation. This work presents a numerical model and numerical procedures to solve such a kind of self-contact in beams under loop formation. Numerical examples are presented in the context of initially straight nitinol beams. Numerical tests showed that friction may influence loop and snarling formation. Numerical models could predict self-contact occurrence events with good agreement with experimental results already published in literature. Snarling patterns (when occurred) were also predicted correctly, but with delay when compared to experiments. This delay showed to be friction-dependent.

















Similar content being viewed by others
Notes
Alternatively one could also write the virtual power theorem, leading to different equations. This was done for instance in [19].
It was considered that the derivatives of matrices \({\varvec{\Psi } }^{\mathbf{i}+\mathbf{1}}\) and \({\varvec{\Upsilon }}^{\mathbf{i}+\mathbf{1}}\) have no important contributions to the tangent operator. The classical Newmark method was applied as described, considering the inertial and damping matrices. However, strictly speaking, the tangent operator should also contain Gateaux derivatives components from damping and inertia matrices, which were not considered. This does not imply in wrong solutions, once the weak form is complete and includes all contributions. The only possible implication would be a non-quadratic asymptotic convergence rate. However, good convergence rate was achieved in numerical examples here developed, even including large nonlinear behavior.
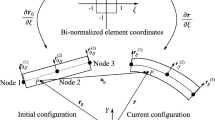
The solution \((\upzeta _{1\mathrm{c}},{\upzeta }_{2\mathrm{c}})\) is not necessarily unique, once it depends on the nature of the curves. For straight non-parallel beams the solution is unique but, for generic spatial curves one can have multiple points obeying criterion for local minimum distance points. The present work assumes, as Zavarise and Wriggers [28], that beams are parameterized as straight lines for contact detection purposes, even after suffering bending. Clearly this is a geometric approximation, which should lead to good results in cases of meshes with small-length beam elements.
This parameterization is used only in the contact evaluation of the here utilized model. It is completely different and independent from the parameterization used in structural model, presented in Sect. 2. For the simulations here presented, e.g., quadratic isoparametric interpolation was assumed for structural model, which is not consistent with the linear interpolation here assumed. This inconsistency, however, does not represent a drawback, once contact detection and structural interpolation are absolutely independent terms in problem weak form and can be with no problems be treated this way. Some tests were performed for frictionless contact considering higher order polynomials. However, increasing the interpolation degree would give a more precise contact detection, but does not ensure smoothness between beam elements, which could be achieved by Hermite interpolation using neighbor elements, such as done in [30]. This technique was not here applied and can be an object of future work.
To shorten notation \(\mathbf{z}_{\mathbf{1}}^{\mathbf{i}+\mathbf{1}} ({\upzeta }_{1\hbox {c}} )\) and \(\mathbf{z}_{\mathbf{2}}^{\mathbf{i}+\mathbf{1}} ({\upzeta }_{2\hbox {c}} )\) are simply written by \(\mathbf{z}_{\mathbf{1}}^{\mathbf{i}+\mathbf{1}} \) and \(\mathbf{z}_{\mathbf{2}}^{\mathbf{i}+\mathbf{1}}\). All calculations involving gap function and its consistent linearization (leading to the tangent operator) for contact computation are evaluated using \({\upzeta }_{1\hbox {c}}\) and \({\upzeta }_{2\hbox {c}}\) values.
The parameters are related to the initial-touch position on both beams. These values have to be reset and re-set in case of losing and re-establishing contact. Furthermore, the actual beam has non-null cross section dimensions and, even small, strictly speaking will not lead to a line to line interaction, as implicitly modeled by the here used approach. Physically the contact interaction takes place on both beams external surface. Then, a more elaborated tangential gap function would have to consider the actual surface points of contact in both beams, mapping then on surfaces. This kinematics is absolutely more complicated than the proposed by Zavarise and Wriggers [28] approach. The real importance of such an effect, however, may take place only in problems with larger dimensions of cross section (when compared to beam length) or situations in which torsion and rolling may occur. An enhanced kinematic description involving ideas to be generalized to beam to beam contact is presented by Gay Neto et al. [37].
Pinball radius value, once enough for detecting contact properly, does not affect contact forces, gap calculations, etc. It is only a first detection tool to help in efficiency of contact detection.
Initial conditions (displacement and velocity) of point “B” were considered to be null in the beginning of the third load-step. One can note that Fig. 8 imposed displacement is not a ramp loading, but a composition of a null derivative function in origin—actually a polynomial of second order, until the time achieves 1 s, followed by a constant slope function until the time 4.5 s is achieved. This imposed displacement series avoids a jerk in the very beginning of dynamics which could be done in a traditional ramp loading. This time-series showed smoother oscillation results along time than a traditional “ramp”. This was very useful, once dealing with a very low damping rate.
References
Love AEH (1944) A treatise on the mathematical theory of elasticity. Dover publications, New York
Liu FC (1975) Kink formation and rotational response of single and multi-strand electromechanical cables. Technical Note N-1403, Civil Engineering Lab, Naval Construction Batallion Center
Ross AL (1977) Cable kinking analysis and prevention. J Eng Ind 99:112–115
Yabuta T (1984) Submarine cable kink analysis. Bulletin of JSME 27:1821–1828
Coyne J (1990) Analysis of the formation and elimination of loops in twisted cable. IEEE J Ocean Eng 15:72–83
Thompson JMT, Champneys AR (1996) From helix to localized writhing in the torsional post-buckling of elastic rods. Proc R Soc Lond A 452:117–138 [Royal Society Publishing]
Goss VGA, van der Heijden GHM, Thompson JMT, Neukirch S (2005) Experiments on snap buckling, hysteresis and loop formation in twisted rods. Exp Mech 45(2):101–111
van der Heijden GHM, Neukirch S, Goss VGA, Thompson JMT (2003) Instability and self-contact phenomena in the writhing of clamped rods. Int J Mech Sci 45:161–196
Gay Neto A, Martins CA (2013) Structural stability of flexible lines in catenary configuration under torsion. Mar Struct 34:16–40
Miyazaki Y, Kondo K (1997) Analytical solution of spatial elastica and its application to kinking problem. Int J Solid Struct 27:3619–3636
Goyal S, Perkins NC, Lee CL (2008) Non-linear dynamic intertwining of rods with self-contact. Int J Nonlinear Mech 43:65–73
Antman SS (1974) Kirchhoff’s problem for nonlinearly elastic rods. Q Appl Math 32:221–240
Simo JC (1985) A finite strain beam formulation. Three-dimensional dynamic problem. Part I. Comput Methods Appl Mech Eng 49:55–70
Vu-Quoc L, Simo JC (1987) On the dynamics of Earth-orbiting flexible satellites with multibody components. AIAA J Guidance Control Dyn 10(6):549–558 paper G87–088
Simo JC, Vu-Quoc L (1986) Three-dimensional finite-strain rod model. Part II: Computational aspects. Comput Methods Appl Mech Eng 58(1):79–116
Simo JC, Vu-Quoc L (1988) On the dynamics in space of rods undergoing large motions-A geometrically exact approach. Comput Methods Appl Mech Eng 66:125–161
McRobie FA, Lasenby J (1999) Simo-Vu Quoc rods using Clifford algebra. Int J Numer Methods Eng 45(4):377–398
Pimenta PM, Yojo T, Pimenta PM (1993) Geometrically exact analysis of spatial frames. Appl Mech Rev 46:118–128
Pimenta PM, Campello EMB, Wriggers P (2008) An exact conserving algorithm for nonlinear dynamics with rotational DOF’s and general hyperelasticity. part 1: Rods. Comput Mech 42:715–732
Gay Neto A, Martins CA, Pimenta PM (2014) Static analysis of offshore risers with a geometrically-exact 3D beam model subjected to unilateral contact. Comput Mech 53:125–145
Chamekh M, Mani-Aouadi S, Moakher M (2014) Stability of elastic rods with self-contact. Comput Methods Appl Mech Eng 279:227–246
Gay Neto A, Pimenta PM, Martins CA (2013) Loop formation in catenary risers on installation conditions: a comparison of statics and dynamics. Proceedings of the \(32^{nd}\) International Conference on Ocean, Offshore and Arctic Engineering
Wriggers P (2008) Nonlinear Finite Element Methods. Springer-Verlag, Berlin Heidelberg
Pimenta PM, Campello EMB (2001) Geometrically nonlinear analysis of thin-walled space frames. Proceedings of the Second European Conference on Computational Mechanics, II ECCM, Krakow
Campello EMB, Pimenta PM, Wriggers P (2003) A triangular finite shell element based on a fully nonlinear shell formulation. Comput Mech 31:505–518
Pauletti RM, Pimenta PM (1995) Formulação de um elemento finito de cabo incorporando o efeito do atrito. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería 11(4):565–576
Wriggers P, Zavarise G (1997) On contact between three-dimensional beams undergoing large deflections. Commun Numer Methods Eng 13:429–438
Zavarise G, Wriggers P (2000) Contact with friction between beams in 3-D space. Int J Numer Methods Eng 49:977–1006
Litewka P, Wriggers P (2002) Friction contact between 3D beams. Comput Mech 28:26–39
Litewka P (2007) Hermite polynomial smoothing in beam-to-beam frictional contact. Comput Mech 40:815–826
Konyukhov A, Schweizerhof K (2008) On the solvability of closest point projection procedures in contact analysis: analysis and solution strategy for surfaces of arbitrary geometry. Comput Methods Appl Mech Eng 197:3045–3056
Konyukhov A, Schweizerhof K (2010) Geometrically exact covariant approach for contact between curves. Comput Methods Appl Mech Eng 199:2510–2531
Litewka P (2013) Enhanced multiple-point beam-to-beam frictionless contact finite element. Comput Mech 52:1365–1380
Durville D (2012) Contact-friction modeling within elastic beam assemblies: an application to knot tightening. Comput Mech 49:687–707
Wriggers P (2002) Computational contact mechanics. Wiley, West Sussex
Belytschko T, Neal MO (1991) Contact-impact by the Pinball algorithm with penalty and Lagrangian methods. Int J Numer Methods Eng 31:547–572
Gay Neto A, Pimenta PM, Wriggers P (2014) Contact between rolling beams and flat surfaces. Int J Numer Methods Eng 97:683–706
Acknowledgments
The authors acknowledge FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo) for the support under the Grants 2012/09912-0 and 2014/11910-0. The second author acknowledges also the support by CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) under the Grant 303091/2013-4.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (mp4 2096 KB)
Rights and permissions
About this article
Cite this article
Gay Neto, A., Pimenta, P.M. & Wriggers, P. Self-contact modeling on beams experiencing loop formation. Comput Mech 55, 193–208 (2015). https://doi.org/10.1007/s00466-014-1092-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-014-1092-3