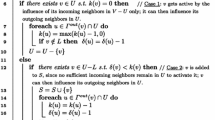Skip to main content
SpringerLink
Log in

Discovering Small Target Sets in Social Networks: A Fast and Effective Algorithm

  • Published:
Algorithmica Aims and scope Submit manuscript

Abstract

Given a network represented by a graph \(G=(V,E)\), we consider a dynamical process of influence diffusion in G that evolves as follows: Initially only the nodes of a given \(S\subseteq V\) are influenced; subsequently, at each round, the set of influenced nodes is augmented by all the nodes in the network that have a sufficiently large number of already influenced neighbors. The question is to determine a small subset of nodes S (a target set) that can influence the whole network. This is a widely studied problem that abstracts many phenomena in the social, economic, biological, and physical sciences. It is known that the above optimization problem is hard to approximate within a factor of \(2^{\log ^{1-\epsilon }|V|}\), for any \(\epsilon >0\). In this paper, we present a fast and surprisingly simple algorithm that exhibits the following features: (1) when applied to trees, cycles, or complete graphs, it always produces an optimal solution (i.e, a minimum size target set); (2) when applied to arbitrary networks, it always produces a solution of cardinality which improves on previously known upper bounds; (3) when applied to real-life networks, it always produces solutions that substantially outperform the ones obtained by previously published algorithms (for which no proof of optimality or performance guarantee is known in any class of graphs).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Notes

  1. Notice that in each of Cases 1, 2, and 3 ties are broken at random.

References

  1. Ackerman, E., Ben-Zwi, O., Wolfovitz, G.: Combinatorial model and bounds for target set selection. Theor. Comput. Sci. 411(44–46), 4017–4022 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bazgan, C., Chopin, M., Nichterlein, A., Sikora, F.: Parameterized approximability of maximizing the spread of influence in networks. J. Discrete Algorithms 27, 54–65 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  3. Ben-Zwi, O., Hermelin, D., Lokshtanov, D., Newman, I.: Treewidth governs the complexity of target set selection. Discrete Optim. 8(1), 87–96 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bond, R.M., Fariss, C.J., Jones, J.J., Kramer, A.D.I., Marlow, C., Settle, J.E., Fowler, J.H.: A 61-million-person experiment in social influence and political mobilization. Nature 489, 295–298 (2012)

    Article  Google Scholar 

  5. Centeno, C.C., Dourado, M.C., Penso, L.D., Rautenbach, D., Szwarcfiter, J.L.: Irreversible conversion of graphs. Theor. Comput. Sci. 412(29), 3693–3700 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen, N.: On the approximability of influence in social networks. SIAM J. Discrete Math. 23(3), 1400–1415 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen, W., Lakshmanan, L.V., Castillo, C.: Information and Influence Propagation in Social Networks. Morgan & Claypool, San Rafael (2013)

  8. Chiang, C.-Y., Huang, L.-H., Li, B.-J., Jiaojiao, W., Yeh, H.-G.: Some results on the target set selection problem. J. Comb. Optim. 25(4), 702–715 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chiang, C.-Y., Huang, L.-H., Yeh, H.-G.: Target set selection problem for honeycomb networks. SIAM J. Discrete Math. 27(1), 310–328 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chopin, M., Nichterlein, A., Niedermeier, R., Weller, M.: Constant thresholds can make target set selection tractable. Theory Comput. Syst. 55(1), 61–83 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  11. Christakis, N.A., Fowler, J.H.: Connected: The Surprising Power of Our Social Networks and How They Shape Our Lives—How Your Friends’ Friends’ Friends Affect Everything You Feel, Think, and Do. Back Bay Books (reprint edition) (2011)

  12. Cicalese, F., Cordasco, G., Gargano, L., Milanič, M., Peters, J., Vaccaro, U.: Spread of influence in weighted networks under time and budget constraints. Theor. Comput. Sci. 586, 40–58 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cicalese, F., Cordasco, G., Gargano, L., Milanič, M., Vaccaro, U.: Latency-bounded target set selection in social networks. Theor. Comput. Sci. 535, 1–15 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  14. Coja-Oghlan, A., Feige, U., Krivelevich, M., Reichman, D.: Contagious sets in expanders. In: Proceedings of the Twenty-Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 1953–1987 (2015)

  15. Cordasco, G., Gargano, L., Mecchia, M., Rescigno, A.A., Vaccaro, U.: A fast and effective heuristic for discovering small target sets in social networks. In: Proceedings of International Conference on Combinatorial Optimization and Applications, COCOA 2015, vol. 9486, pp. 193–208 (2015)

  16. Cordasco, G., Gargano, L., Rescigno, A.A., Vaccaro, U.: Optimizing spread of influence in social networks via partial incentives. In: Structural Information and Communication Complexity: 22nd International Colloquium, SIROCCO 2015, pp. 119–134 (2015)

  17. Cordasco, G., Gargano, L., Rescigno, A.A., Vaccaro, U.: Brief announcement: active information spread in networks. In: Proceedings of the 2016 ACM Symposium on Principles of Distributed Computing, PODC, vol. 16, pp. 435–437 (2016)

  18. Cordasco, G., Gargano, L., Rescigno, A.A., Vaccaro, U.: Evangelism in social networks. In: Proceedings of Combinatorial Algorithms—27th International Workshop, IWOCA 2016, pp. 96–108 (2016)

  19. Cordasco, G., Gargano, L., Rescigno, A.A.: On finding small sets that influence large networks. Soc. Netw. Anal. Min. SNAM 6(94), 2016 (2016)

    Google Scholar 

  20. Dinh, T.N., Zhang, H., Nguyen, D.T., Thai, M.T.: Cost-effective viral marketing for time-critical campaigns in large-scale social networks. IEEE/ACM Trans. Netw. 22(6), 2001–2011 (2014)

    Article  Google Scholar 

  21. Domingos, P., Richardson, M.: Mining the network value of customers. In: Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’01, pp. 57–66 (2001)

  22. Easley, D., Kleinberg, J.: Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge University Press, New York (2010)

    Book  MATH  Google Scholar 

  23. Fan, L., Weili, W., Zhai, X., Xing, K., Lee, W., Ding-Zhu, D.: Maximizing rumor containment in social networks with constrained time. Soc. Netw. Anal. Min. 4(1), 214 (2014)

    Article  Google Scholar 

  24. Gargano, L., Hell, P., Peters, J.G., Vaccaro, U.: Influence diffusion in social networks under time window constraints. Theor. Comput. Sci. 584(C), 53–66 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  25. Granovetter, M.: Threshold models of collective behavior. Am. J. Sociol. 83(6), 1420–1443 (1978)

    Article  Google Scholar 

  26. Kempe, D., Kleinberg, J., Tardos, É.: Maximizing the spread of influence through a social network. In: Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’03, pp. 137–146, New York, NY, USA (2003)

  27. Kempe, D., Kleinberg, J., Tardos, É.: Influential nodes in a diffusion model for social networks. In: Proceedings of the 32nd International Conference on Automata, Languages and Programming, ICALP’05, pp. 1127–1138, Berlin, Heidelberg (2005)

  28. Lately, D.: An Army of Eyeballs: The Rise of the Advertisee. The Baffler, Chicago (2014)

    Google Scholar 

  29. Leppaniemi, M., Karjaluoto, H., Lehto, H., Goman, A.: Targeting young voters in a political campaign: empirical insights into an interactive digital marketing campaign in the 2007 finnish general election. J. Nonprofit Public Sect. Market. 22(1), 14–37 (2010)

    Article  Google Scholar 

  30. Leskovec, J., Krevl, A.: SNAP Datasets: Stanford Large Network Dataset Collection (2015). http://snap.stanford.edu/data

  31. Leskovec, J., Adamic, L.A., Huberman, B.A.: The dynamics of viral marketing. ACM Trans. Web 1(1), 5 (2007)

    Article  Google Scholar 

  32. Lu, Z., Wu, W.: Influence maximization. In: Kao, M.-Y. (ed.) Encyclopedia of Algorithms. Springer, Berlin (2014)

    Google Scholar 

  33. Mark, E.J.: Newman modularity and community structure in networks. Proc. Natl. Acad. Sci. USA (PNAS) 103(23), 8577–8582 (2006)

    Article  Google Scholar 

  34. Nichterlein, A., Niedermeier, R., Uhlmann, J., Weller, M.: On tractable cases of target set selection. Soc. Netw. Anal. Min. 3(2), 233–256 (2013)

    Article  MATH  Google Scholar 

  35. Reddy, T.T., Pandu Rangan, C.: Variants of spreading messages. J. Gr. Algorithms Appl. 15(5), 683–699 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  36. Shakarian, P., Eyre, S., Paulo, D.: A scalable heuristic for viral marketing under the tipping model. Soc. Netw. Anal. Min. 3(4), 1225–1248 (2013)

    Article  Google Scholar 

  37. Sorokin, A., Murphey, R., Thai, M.T., Pardalos, P. (eds.): Dynamics of Information Systems: Mathematical Foundations. Springer, Berlin (2012)

    MATH  Google Scholar 

  38. Tumulty, K.: Obama’s Viral Marketing Campaign. TIME Magazine, New York (2007)

    Google Scholar 

  39. Wasserman, S., Faust, K.: Social Network Analysis: Methods and Applications. Cambridge University Press, Cambridge (1994)

    Book  MATH  Google Scholar 

  40. Zafarani, R., Liu, H.: Social computing data repository at ASU (2009). http://socialcomputing.asu.edu

  41. Zaker, M.: On dynamic monopolies of graphs with general thresholds. Discrete Math. 312(6), 1136–1143 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  42. Zhang, H., Mishra, S., Thai, M.T.: Recent advances in information diffusion and influence maximization in complex social networks. In: Wu, J., Wang, Y. (eds.) Opportunistic Mobile Social Networks. CRC Press, Boca Raton (2014)

    Google Scholar 

  43. Zhu, Y., Weili, W., Bi, Y., Lidong, W., Jiang, Y., Wen, X.: Better approximation algorithms for influence maximization in online social networks. J. Comb. Optim. 30(1), 97–108 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We are grateful to the reviewers for their careful reading of the paper and for their helpful comments.

Author information

Authors and Affiliations

  1. Department of Psychology, Università degli Studi della Campania “Luigi Vanvitelli”, Caserta, Italy

    Gennaro Cordasco

  2. Department of Computer Science, University of Salerno, Fisciano, Italy

    Luisa Gargano, Marco Mecchia, Adele A. Rescigno & Ugo Vaccaro

Authors
  1. Gennaro Cordasco
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luisa Gargano
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marco Mecchia
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Adele A. Rescigno
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ugo Vaccaro
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ugo Vaccaro.

Additional information

A preliminary version of this paper was presented at the 9th Annual International Conference on Combinatorial Optimization and Applications (COCOA’15), December 18–20, 2015, Houston, Texas, USA.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cordasco, G., Gargano, L., Mecchia, M. et al. Discovering Small Target Sets in Social Networks: A Fast and Effective Algorithm. Algorithmica 80, 1804–1833 (2018). https://doi.org/10.1007/s00453-017-0390-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00453-017-0390-5

Keywords

Search

Navigation