Introduction

Active volcanoes produce a great variety of infrasound signals during degassing and eruptive activity. To a first approximation, volcano infrasound signals can be characterized as (i) short-duration transients or (ii) long-duration tremors (McNutt et al. 2015). The short-duration transients are characterized by a rapid compression of the atmosphere followed by decompression and a gradually decaying coda with a duration of a few seconds to minutes. They are caused by discrete explosive events or bursting of large gas slugs (Fee and Matoza 2013). Long-duration tremor consists of a continuous vibration of the atmosphere lasting anywhere from seconds to months and is generated by a wide range of processes including continuous unsteady degassing, roiling of a lava lake surface, overlapping or closely spaced discrete explosive events, lava fountaining, and jet noise during sustained eruption columns (Fee and Matoza 2013; Garces et al. 2013). Different types of infrasonic tremor exist and are classified based on their time and frequency domain characteristics (harmonic tremor, monotonic tremor, broadband tremor, and spasmodic tremor; Johnson and Ripepe 2011; Fee and Matoza 2013).

During the last few decades, the study of infrasonic activity has played an important role for volcano research and monitoring purposes (e.g., Johnson and Ripepe 2011; Cannata et al. 2013; Fee and Matoza 2013; McNutt et al. 2015; Ripepe et al. 2018; Watson et al. 2022). In particular, researchers estimated eruptive parameters, such as plume height (Caplan-Auerbach et al. 2010), eruption mass rate (Fee et al. 2017), magma discharge rate (Ripepe et al. 2013), and lava fountain height (Sciotto et al. 2019) from infrasound amplitude observations or compared infrasonic data with other eruptive parameters (Ichihara 2016). For instance, Caplan-Auerbach et al. (2010) estimated volume flux and plume height from infrasonic recordings of the 2006 eruption of Augustine (Alaska). By using infrasound signals integrated with other data, Ripepe et al. (2013) calculated the plume exit velocity and mass eruption rate for the 2010 Eyjafjallajokull eruption in Iceland. Fee et al. (2017) used numerical Green’s functions that described acoustic wave propagation over realistic topography to invert infrasound observations for the erupted volumetric flow rate at Sakurajima (Japan) in 2015.

While infrasound signals can propagate hundreds or thousands of kilometers in the atmosphere, many volcano infrasound studies have focused on local observations where infrasound sensors are located within 15 km of the vent (Matoza et al. 2019; Johnson 2019). For local volcano infrasound studies, sensors are usually positioned on the flanks of volcanoes, where the topography is pronounced, and hence infrasonic signals can be strongly affected by the local topography (e.g., Fee and Matoza 2013; Lacanna and Ripepe 2013; Fee et al. 2017; Matoza et al. 2019; Ishii et al. 2020; Maher et al. 2021; Khodr et al. 2022). Infrasonic waveforms can experience diffraction or reflection due to the topographic barriers of volcanoes such as crater edges, ridges, and hills (Kim and Lees 2011; Kim et al. 2012; Spina et al. 2015). Accounting for topographic scattering is necessary to obtain accurate infrasound-derived source locations and volume rates (Kim et al. 2015; Fee et al. 2017, 2021).

Active volcanoes can undergo rapid changes in topography due to eruptions and mass movements (Wadge et al. 2011; Ebmeier et al. 2012). Although several studies have demonstrated how the interaction of infrasonic signals with the topography between the receiver and the source can significantly affect their propagation at local scales (Kim et al. 2015; Fee et al. 2021), the impact of changes in topography on the infrasonic signal has only been explored in very few cases (Gestrich et al. 2022; McKee et al. 2023).

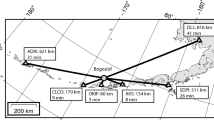
Mt. Etna (Italy) is an exceptional natural laboratory to investigate how changes in topography impact the observed infrasound signal. Since 2006, the Istituto Nazionale di Geofisica e Vulcanologia, Osservatorio Etneo (INGV-OE), has been recording and analyzing the infrasonic signal from Mt. Etna by using a permanent network composed of microphones distributed at different distances from the summit craters over almost all the volcano flanks (Fig. 1). Infrasonic volcanic tremor, accompanying the seismic volcanic tremor, has been recorded on Mt. Etna during lava fountaining episodes (also called lava fountains or paroxysms in this paper), banded seismic tremor, and degassing activities (e.g., Cannata et al. 2009, 2010; Sciotto et al. 2019). Eruptive activity occurs frequently at Mt. Etna from the numerous vents within the summit craters (Voragine (VOR); Bocca Nuova (BN); North East Crater (NEC); South East Crater (SEC); inset in Fig. 1), as well as along eruptive fissures that open on the flanks of the volcano (Andronico et al. 2021). Mt. Etna is a highly dynamic environment that has rapid and significant changes in topography (Behncke et al. 2014; Neri et al. 2017; Ganci et al. 2022).

Fig. 1
figure 1

Shaded relief of Mt. Etna (Gwinner et al. 2006) with the locations of the infrasound stations used in this work (red triangles). The inset in the upper right corner shows the summit area, updated on 16 September 2021: South-East Crater (SEC); Bocca Nuova (BN); Voragine (VOR); and North-East Crater (NEC)

Full size image

In this paper, we analyze infrasonic signals recorded at Mt. Etna during 57 paroxysmal lava fountains between 16 February and 23 October 2021, investigate how the near-vent topography changed throughout the eruptive sequence, and discuss the impact of changes in topography, infrasonic source location, and amplitude on the observed infrasound signal.

Volcanic framework

Mt. Etna is known for its persistent and variable eruptive activity from both the summit craters and the flanks of the volcano. Summit eruptions can last from a few hours to several months and are characterized by degassing phases alternated with Strombolian activity, lava overflows, and lava fountains (e.g., Harris et al. 2011; Behncke et al. 2014; Andronico et al. 2021). Over the past 20 years, frequent lava fountain events (also called paroxysms) have occurred at the summit craters of Mt. Etna with the majority occurring at the SEC (Andronico et al. 2021). Between 2011 and 2016, a series of paroxysms gave rise to a new pyroclastic cone at the eastern base of the SEC, initially called New South East Crater (NSEC). Over the last few years, the NSEC progressively coalesced with the SEC.

On 13 December 2020, lava fountaining activity resumed at SEC (Calvari et al. 2021). Additional episodes of lava fountains occurred on 14, 21, and 22 December 2020 and on 18 January 2021 (Bonaccorso et al. 2021). Eruptive activity at Mt. Etna during 2021 was characterized by 57 paroxysms that took place at the SEC from 16 February to 23 October and gave rise to lava flows that propagated to the East, South, and South-West. The eruptive activity was characterized by lava fountains that were heterogeneous in duration, number of active vents, and height of jets and eruptive columns (Andronico et al. 2021; Bonaccorso et al. 2021; Calvari and Nunnari 2022; Calvari et al. 2022). These paroxysms can be divided into two sequences based on lava output rates: the first one from 16 February to 1 April 2021, and the second one from 19 May to 23 October 2021. Ganci et al. (2023) estimated that the average output rate is 7.2 m3/s in the first sequence, while it is 2.9 m3/s during the second sequence. Guerrieri et al. (2023) retrieved the volcanic cloud top height, the ash, ice, and SO2 mass time series and the cumulative masses for the whole period. The retrievals indicate that the first episodes of the eruptive activity attained the highest values in all of these listed parameters. Musu et al. (2023) investigated the evolution of the magmatic system during the first sequence of paroxysms from a mineral chemistry perspective. They propose this eruptive sequence was initiated by the injection of a hotter and deeper magma in a storage volume at 1–3 kbar. In this work, we analyze the infrasonic signals recorded during the 2021 paroxysms.

As described by Alparone et al. (2003), each lava fountain episode can be divided into three main eruptive phases: (i) resumption phase, (ii) paroxysmal phase, and (iii) conclusive phase. The resumption phase, lasting from tens of minutes to a few days, is characterized by low-intensity episodic explosions that begin to open the volcanic conduit and by the gradual increase in volcanic tremor amplitude, which corresponds to an increase in explosive activity. During the paroxysmal phase, generally lasting from 10 to 60 min, a transition from Strombolian explosions to sustained lava fountains takes place. During this phase, the amplitude of volcanic tremor reaches its maximum peak. This phase is characterized by a sharp increase in effusive activity; the creation of a sustained column of ash, lapilli, and steam (up to 4.5 to 15 km a.s.l.); and pyroclastic fallout. Lava flows may also precede the onset of lava fountaining (Behncke et al. 2014). The third phase is characterized by a return to Strombolian activity, a decrease in volcanic tremor amplitude to the background level (i.e., those before the paroxysm onset), and finally cessation of the eruptive episode.

Data and methods

Topographic data

During 2021, several topographic surveys were performed with unoccupied aerial systems (UAS) for monitoring purposes in order to understand the structure and evolution of the SEC summit area. We focus on two surveys performed on 3 March 2021 and 16 September 2021 when 60 and 365 images were collected respectively, to produce digital surface models (DSMs) of the SEC crater.

The 3 March 2021 and the 16 September 2021 DSMs had a resolution of 0.55 m and 0.44 m, respectively. Safety considerations meant that there was only limited time for the UAS surveys and hence the UAS-derived DSMs are focused on the SEC cone. The SEC morphology was profoundly modified from 2020 and therefore it is not possible to identify unchanged areas for comparing DSM accuracy with previous topographic surveys. We assume that the accuracy is comparable with that (1.5–1.8 m) previously measured for UAS-derived DSMs of Mt. Etna (De Beni et al. 2020).

Best practices in photogrammetric UAS surveys (e.g., Huang et al. 2017) are to have ground control points (GCPs) spread evenly throughout the survey area. Due to safety constraints when operating on an active volcano, this was not possible. In order to improve the georeferencing and extend the spatial coverage of the UAS-derived DSMs, we integrated them with a satellite-derived DSM and aligned the DSMs by applying dense cloud techniques (De Beni et al. 2019; Fig. 2). The satellite-derived DSM was obtained by processing a Pléiades triplet acquired on 22 August 2020. These high-resolution satellite images provide three along-track views (before nadir, nadir, and after nadir) of the same target area at 0.5-m spatial resolution and can be processed using photogrammetric techniques to reconstruct the three dimensional surface of the target (Ganci et al. 2019a). We used the MicMac open-source library (Rupnik et al. 2017) to process the Pleiades triplet and obtain a 1-m spatial resolution DSM of Mt. Etna volcano. The vertical accuracy of this DSM is about 1 m and was computed considering the standard deviation of the difference between this DSM and a previous one, validated in those areas where no topographic changes occurred (Ganci et al. 2019b).

Fig. 2
figure 2

Shaded relief of the summit area of Mt. Etna obtained through the integration of the 22 August 2020 Pleiades DSM with the DSMs resulting from the UAS surveys performed on 3 March (a) and 16 September (b) 2021. c Height difference (HD) between the September and March DSMs. The red dots in a and b indicate the prevailing source location during the first and the second eruptive sequences, respectively. Coordinate system UTM WGS 84 33N

Full size image

During the two eruptive sequences, the SEC morphology changed dramatically. Until 3 March 2021, the external crater rim had a bean shape elongated for about 300 m in ENE-WSW direction and with minimum axis of about 170 m (Sciotto et al. 2022). Considering the video observations and the crater morphology, we can assume that the prevailing source of the lava fountains of the first eruptive sequence was located on the eastern portion of the crater (see red dot in Fig. 2a). The eastern portion of the crater rim was preserved with a ridge of about 35 m. The following volcanic activity filled this crater with a stack of volcanics about 90 m thick, building a plateau. Observation of the lava fountain by the permanent camera of the INGV-OE showed a shifting of the vent of about 200 m towards south west (see red dot in Fig. 2b). The 16 September DSM clearly shows a 60-m-deep scar in the south west flank of the SEC that is about 220 m long. By subtracting the two DSMs previously aligned, a vertical difference ranging from 0 up to 116 m was obtained (Fig. 2c).

Geophysical data and methods

Infrasonic signals accompanying 57 paroxysmal activities at Mt. Etna in 2021 were analyzed. In particular, the analyses were performed on the recordings from 7 stations (ECNE, ECPN, EMFO, EMFS, EPLC, ESLN, ESVO; Fig. 1) located at distances ranging from 1 to 8 km from SEC. Each station is equipped with a GRASS 40AN microphone with a flat response with a sensitivity of 50 mV/Pa in the frequency range 0.3–20,000 Hz (sampling rate equal to 50 Hz).

The paroxysmal episodes analyzed occurred in two distinct sequences: the first sequence began on 16 February and ended on 1 April 2021 and was characterized by 17 paroxysms with intervals from a few hours to 7 days; the second sequence began on 19 May and ended on 23 October 2021. In this sequence, 40 paroxysmal episodes occurred, with intervals ranging from a few hours to almost one month. Between the two sequences, the location of the main eruptive vent moved and the topography of the SEC changed significantly (Fig. 2).

Most of the analyzed paroxysmal events were recorded by all the above-mentioned 7 stations, except in some cases when only a subset of stations were functioning (Fig. S1). To define the amplitude of the infrasonic signals recorded during the paroxysms, we calculated the quadratic-reduced pressures as follows. First of all, the root mean square (RMS) amplitude was calculated as:

$$RMS=\sqrt{\frac{\sum_{n=0}^{N-1}{\left({s}_n^F\right)}^2}{N}}$$
(1)

where \({s}_n^F\) is the filtered infrasound signal, and N is the number of samples in the signal window. Infrasonic signals are considered stationary (Battaglia and Aki 2003).

The RMS amplitudes were calculated over 81.92-s-long sliding windows and the signals were filtered between 0.5 and 5 Hz (it has been shown that most of the energy of such signals is contained in this frequency band; Cannata et al. 2009, 2013). To produce more stable amplitude time series describing the pattern of the infrasonic tremor throughout each paroxysmal episode, RMS values were averaged across 5-min-long time windows (RMSav). Finally, to compute the quadratic reduced pressures (QRP), the average RMS amplitudes were multiplied by the source-station distance (r) and squared to be proportional to signal energy:

$$QRP={\left({RMS}_{av}\times r\right)}^2$$
(2)

According to the location of the main eruptive vent during the two eruptive sequences, the acoustic sources were considered to be located in SEC but at slightly different positions for the two sequences (Fig. 2). An example of infrasonic signals and corresponding spectrogram, RMS, and QRP time series is shown in Fig. 3.

Fig. 3
figure 3

a Infrasonic signals of the 22–23 May 2021 lava fountain recorded by the EMFO station, b corresponding spectrogram, c RMS amplitude, and d QRP time series

Full size image

For each paroxysmal episode, we calculated the maximum value of quadratic-reduced pressures (QRPmax; unit Pa2 m2) and the cumulative quadratic-reduced pressures (QRPcum; unit Pa2 m2 s) (Fig. 4). For the QRPcum, the interval analyzed for each episode had a duration of 6 h: 3 h before and 3 h after the peak of each eruptive event. Figure 4 shows that for stations ECPN and EMFO, the first paroxysmal episodes in each sequence were characterized by low values of QRP (maximum and cumulative) and during each sequence the amplitudes gradually increase.

Fig. 4
figure 4

Variation over time of a QRPcum for ECPN, b QRPmax for ECPN, c QRPcum for EMFO, and d QRPmax for EMFO. The vertical black line indicates the boundary between the first and the second sequences

Full size image

We computed the mean value of QRPmax and QRPcum for each station during the first (17 paroxysms, 16 February to 1 April) and the second (40 paroxysms, 19 May to 23 October) eruptive sequences. We then calculated the ratio between the QRP, for both cumulative and maximum values, between the first and second sequences of paroxysmal episodes (Fig. 5). The infrasonic signal during the considered time windows is dominated by the infrasonic eruptive tremor, as also observed during previous lava fountain activities. The Strombolian phases preceding and following the paroxysmal phases are characterized by infrasonic events (Cannata et al. 2009; Sciotto et al. 2019).

Fig. 5
figure 5

Contour maps of Mt. Etna with the locations of the infrasonic stations (colored dots). The color of the dots indicates the ratio between a QRPcum and b QRPmax between the first and the second eruptive sequences. Coordinate system UTM WGS 84 33N

Full size image

Modeling of infrasound signals

In order to examine the influence of the changing topography (Fig. 2) on the observed infrasound signal, we performed numerical simulations of the acoustic wavefield. We use infraFDTD (Kim and Lees 2011; Kim and Lees 2014), which is a 3D linear acoustic wave propagation code that handles realistic topography (with the staircasing approximation) and assumes a rigid boundary between the atmosphere and solid Earth. Absorbing outflow boundary conditions that prevent outgoing waves from reflecting at the computational domain boundary are applied using perfectly matched layers. InfraFDTD has been previously used in multiple volcano infrasound studies (e.g., Kim et al. 2015; Fee et al. 2017, 2021; Diaz-Moreno et al. 2019). The acoustic source is a Blackmann-Harris window function with a frequency of 1 Hz and maximum amplitude of 1 kg/s (infraFDTD is a linear acoustics code, which means that the amplitude of the pressure recorded by the receivers scales linearly with the source amplitude). We used a short-duration monopole source, which radiates acoustic waves isotropically. This is a simplification compared to lava fountains, which are a complex, extended-duration source with a directional radiation pattern (Matoza et al. 2013). We note that infrasonic tremor can be generated by multiple overlapping short-duration sources (e.g., Jolly et al. 2016). Therefore, when considering amplitude ratios, it is appropriate to compare between the observations with the real-world, long-duration lava fountain tremor source and the simulations with the short-duration impulsive source as the observations can be viewed as a superposition of multiple short-duration sources. Hence, rather than considering an arbitrary combination of sources with varying amplitudes and timing, we focus on a single explosive source (for more details see the “Discussion” section). Our simulation domain covers 14 km in the north-south and east-west directions and is centered approximately at the summit of Mt. Etna. The domain stretches from the bottom of the topography at 616 m to a maximum altitude of 4000 m (the maximum topographic elevation is 3362 m). In order to make the simulations computationally tractable, we downsample the high-resolution DSM to a grid spacing of Δx = 18 m, which corresponds to approximately 18 points per wavelength for a 1-Hz acoustic wave (see Wang (1996) and Kim and Lees (2011) for more discussion on sufficient spatial discretization for acoustic wave propagation). This downsampling results in 779 grid points in each horizontal direction and 189 in the vertical direction. The air density is 1.2 kg/m3 and the speed of sound is c = 335 m/s. We use a time step of Δt = 0.03 s, which corresponds to a one-dimensional Courant number of C = cΔt/Δx=0.56. For each station, the QRP is calculated from the simulated pressure time series, p, as QRP = (p × r)2 at each time step. Example pressure time series and QRP are shown in Fig. S2 and Fig. 6a, respectively.

Fig. 6
figure 6

a Simulated QRP for M1 (blue, solid) and S2 (red, dash-dotted). b Ratios between the QRPmax values observed during the first and the second eruptive sequences at the stations belonging to the permanent infrasonic network. c–g Ratios between the QRPmax values computed through 3D acoustic simulations. The plot titles in c–g indicate the details of the simulations: “M” and “S” indicate that the DSMs acquired in March and September 2021, respectively, were used; “1” and “2” indicate that the source locations prevailing during the first and the second eruptive sequences, respectively, were taken into account

Full size image

We examined the two different DSMs (Fig. 2) and denoted the DSM acquired in March “M” and the DSM acquired in September “S.” We also considered the two different source positions and denoted the average source position observed during the first sequence “1” (East coordinate=500,263 m UTM 33N, North coordinate=4,177,693 m UTM 33N) and the average source position observed during the second sequence “2” (East coordinate=500,038 m UTM 33N, North coordinate=4,177,642 m UTM 33N) (see Fig. S3). Between the two sequences, the average source position shifted 231 m to the SW (Fig. 2).

Results

Quadratic reduced-pressure ratios and spatial distribution

We calculated the ratio between the mean QRPcum and QRPmax for the first (17 paroxysms, 16 February to 1 April) and the second (40 paroxysms, 19 May to 23 October) eruptive sequences.

$${\textrm{QRP}}_{\textrm{cum}}\ \textrm{ratio}={\textrm{QRP}}_{\textrm{cum}}\left(\textrm{first}\ \textrm{sequence}\right)/{\textrm{QRP}}_{\textrm{cum}}\left(\textrm{second}\ \textrm{sequence}\right)$$
(3)
$${\textrm{QRP}}_{\textrm{max}}\textrm{ratio}={\textrm{QRP}}_{\textrm{max}}\left(\textrm{first}\ \textrm{sequence}\right)/{\textrm{QRP}}_{\textrm{max}}\left(\textrm{second}\ \textrm{sequence}\right)$$
(4)

The ratios exhibit significant spatial variation, with the QRPcum ratio ranging between 0.5 and 5.2 while the QRPmax ratio ranges from 0.6 to 4.1 (Fig. 5). Values greater than 1 indicate that the QRP is higher during the first sequence than the second sequence. In particular, stations on the southern and eastern flanks of the volcano (EMFO, EMFS, ESLN) exhibit high values of the ratio of both QRPcum and QRPmax.

To verify if the variation in the QRP ratios during the second sequence was gradual or sudden, we subdivided the second sequence into two periods according to Ganci et al. (2023): the first from 19 May to 4 June, and the second from 12 June to 23 October. In Fig. S4 we plotted (i) the QRPcum ratio between the first sequence (1) and the first period of the second sequence (2a) (Fig. S4a); (ii) the QRPcum ratio between the first sequence (1) and the second period of the second sequence (2b) (Fig. S4b); and (iii) the QRPcum ratio between the first period of the second sequence (2a) and the second period of the second sequence (2b) (Fig. S4c). We noted that the difference between the stations in the southern and eastern flanks and the others in the northern and western flanks is visible in Fig. S4a,b. On the other hand, in Fig. S4c, we cannot see any important difference, as the ratios exhibit similar values in all the stations during the two periods of the second sequence.

Changes in the observed infrasound signal amplitudes could be caused by multiple phenomena including changes in topography, source location, source amplitude, and radiation pattern, or propagation conditions, such as winds and atmospheric conditions. From the data, it is challenging to disentangle these multiple phenomena. Hence, we consider numerical simulations of the acoustic wavefield using the source locations, determined from visual and thermal observations, and the topography from the UAS surveys (Fig. 2). In the first simulation, we considered the DSM acquired on 3 March 2021 and the first source location for the first sequence (the simulation indicated as M1). In the second simulation, the DSM acquired on 16 September 2021 and the second source location were used for the second eruptive sequence (the simulation indicated as S2). The ratio between the QRPmax values computed through 3D acoustic simulations, called M1/S2, range from 0.2 to 0.8 (Figs. 6c, 7b), which is significantly less than the ratios observed in the data. Also, it is worth noting that the stations located on the southern and eastern flanks of the volcano show ratio values close to 1, while the others significantly smaller values. Hence, in spite of the absolute difference between observed and computed ratio values, in relative terms, the spatial pattern of the amplitude computed by the numerical simulations is similar to the pattern observed in the recorded data (Fig. 7a, b). We quantified the similarity by computing the correlation coefficient between the QRPmax ratios from the data and simulations (Table 1). For the M1/S2 simulation, the correlation coefficient is 0.96, indicating that the amplitude pattern is very similar between the data and simulations despite the simulated QRPmax ratios being substantially less than for the data.

Fig. 7
figure 7

Contour maps of Mt. Etna with the locations of the infrasonic stations (colored dots). The color of the dots indicates the ratios between the QRPmax values observed during the first and the second sequences (a) and computed through 3D acoustic simulations (b–f). The plot titles in (b–f) indicate the details of the simulations: “M” and “S” indicate that the DSMs acquired in March and September 2021, respectively, were used; “1” and “2” indicate that the source locations prevailing during the first and the second sequences, respectively, were taken into account. Coordinate system UTM WGS 84 33N

Full size image
Table 1 Correlation coefficient between the data QRPmax ratios and simulated QRPmax ratios
Full size table

To better understand the influence of the changes of both topography and source locations, two other simulations were carried out: (i) using the DSM acquired in March 2021 (during the first sequence) and the source location prevailing during the second sequence (M2); (ii) using the DSM acquired in September 2021 (during the second sequence) and the source location prevailing during the first sequence (S1). The QRPmax ratios were calculated for four possible combinations of the simulations: (i) M1/S1 (Figs. 6d, 7c); (ii) M2/S2 (Figs. 6e, 7d); (iii) M1/M2 (Figs. 6f, 7e); (iv) S1/S2 (Figs. 6g, 7f). It is possible to observe different spatial distributions of the synthetic QRP ratios in all the different cases. The spatial distribution that best matches the observed data, as quantified by the correlation coefficient (Table 1), is M1/S2 (Fig. 7b), which is expected as this is the most realistic simulation combination where both the topography and source location change. The second-best match was provided by M2/S2, where the topography changes but the source location is constant (Fig. 7d).

On the basis of the results of all the simulations, the stations located on the southern and eastern flanks (EMFS, ESLN, EMFO) show the ratio M1/S2 close to 1. Such a ratio derives from the opposite role played by the topography changes and the source shift at these stations, whose net effect seems to be to leave the ratio value around 1. On the other hand, at the other stations showing ratio M1/S2 values lower than 1, the effect of the topographic changes is much stronger than the source shift effect. In particular, the low ratio values, meaning an increase in the amplitude computed in S2 compared to the amplitude in M1, could be due to the less effective topographic barrier in S2 and/or to the increasing topographic focusing effects. For the simulations, the QRPmax ratio is less than 1 for all stations, which indicates that the signal is larger during the second sequence, while the observed QRPmax ratios are greater than 1 for almost all stations, which indicates that the signal is larger during the first sequence. For the simulations, we assume that the source amplitude is the same for both sequences. The source amplitude, however, will be variable for the different paroxysmal episodes and the mean value could vary between the two sequences. For example, the observed QRP can vary by an order of magnitude between lava fountains separated by days or hours (Fig. 4). Variations over these short time scales are likely due to variation in the source amplitude rather than changes in the topography. We note that the simulations are performed using a linear wave propagation code, which means that increasing the source amplitude increases the simulated pressure signals by the same factor. Hence, we multiply the pressure signals from the S2 simulation by a scaling factor, α, ranging from 10−2 to 102. The best-fitting scaling factor is chosen to minimize an objective function, Θ,which is defined as the Euclidean norm between the observed and simulated QRPmax ratios for all stations (Fig. 8a):

$$\varTheta ={\left\Vert \textrm{obs}\ {\textrm{QRP}}_{\textrm{max}}-\alpha\ \textrm{sim}\ \textrm{QRPmax}\right\Vert}_2$$
(5)
Fig. 8
figure 8

a Objective function, which is the sum of L2 norm (Euclidean distance) between the observed and simulated QRPmax ratios for all stations, as a function of the scaling parameter α. Lines show the result for the different simulation combinations. b Ratio between the QRPmax values observed during the first and the second eruptive sequences at the stations belonging to the permanent infrasonic network (blue circles) and ratios between the QRPmax values obtained with the simulations M1/S2 with the best-fitting scaling factor for the S2 simulation (α = 0.18; red squares) and M1/S2 without the scaling (yellow triangle). Error bars show the standard deviation in the data, which are exacerbated due to error propagation through division when calculating the QRP ratio

Full size image

The best-fitting scaling factor is α = 0.18 indicating that, on average, the source amplitude during the second sequence is 18% of the amplitude during the first sequence. Scaling the pressure time series of the second eruptive sequence by 0.18 results in a much better match with the observed QRPmax ratios with agreement within error for all stations (Fig. 8b).

Travel time and insertion loss

To better understand the role of the topography and of its variations over time in the simulations, the travel times from the simulations were compared with the travel times predicted by using the slant distance, as was done by Fee et al. (2021). Fig. S5 shows the simulated travel times minus the slant travel times for all the simulations (M1, M2, S1, S2). In M1 simulation (Fig. S5a), travel times are less delayed to the East than to the West, suggesting that during the first sequence the acoustic waves can easily propagate to the East without encountering any major topographic barriers. For S2 (Fig. S5d), the travel time lag to the South and East has increased, suggesting that a topographic barrier has formed and for this reason the acoustic radiation is delayed to the South and East.

Figure 9 shows the difference between the difference of the simulated and slant travel times for S2 and M1 (subtracting Fig. S5a from Fig. S5d). This shows that the difference between the simulated and slant travel times is much higher to the South-East for S2 than for M1, which indicates the hypothesis that the development of a topographic barrier delayed acoustic radiation to the South and East.

Fig. 9
figure 9

Contour map of Mt. Etna with the difference between the difference of the simulated and slant travel times for S2 and M1. The yellow and red dots represent the prevailing source location during the first and the second eruptive sequences, respectively. Coordinate system WGS 84 33N

Full size image

In order to quantify this phenomenon, we evaluated the insertion loss analytically and numerically, and compare the results. We first calculate the Fresnel number, N, using the code of Toney (2022), which is defined as:

$$N=\left({R}_t-{R}_d\right)/\left(\lambda /2\right),$$
(6)

where Rt is the length of the diffracted path, Rd is the length of the direct path (i.e., line-of-sight slant distance), and λ is the wavelength. The lava fountains have a dominant frequency of 1 Hz and hence we use λ = 335 m (as the sound speed used in the simulation is c = 335 m/s). Following Lacanna and Ripepe (2013) and Hantusch et al. (2021), we then calculated the insertion loss (IL) for all the stations using the analytical formula from Maekawa (1968):

$$IL=10\left(3+20N\right)$$
(7)

Previous work by Maher et al. (2021) showed that the Maekawa (1968) model, which was intended for situations when the source and receiver are both in the air, is inappropriate for sound propagation and diffraction over volcanic topography where source and receiver are both located on or near Earth’s surface. Maher et al. (2021) argued that the Maekawa (1968) model overestimates attenuation because it does not account for constructive interference of reflections down the concave volcano slopes that cause focusing of the acoustic energy. Hence, we also calculate the insertion loss numerically as (Lacanna and Ripepe 2013; Maher et al. 2021):

$$IL=-20\ \mathit{\log}\left({p}_s/{p}_r\right)$$
(8)

where ps is the maximum pressure at the station using the topography and pr is the maximum pressure at the station assuming a flat rigid semi-space topography. Simulated pressure time series with topography and for a flat plane are shown in Fig. S2. Positive values of insertion loss indicate that the pressure with topography is smaller than with the flat plane while negative values indicate that the pressure with topography is larger.

Figure 10a and b compare the maximum simulated pressure with topography and for a flat rigid plane. For M1, the maximum pressure with topography is similar to that for a flat plane for the majority of stations except for EMFO, EMFS, and ESLN where the maximum pressure is larger with topography. For S2, the maximum pressure with topography is larger than that for the flat plane for all stations. Figure 10c shows the numerical insertion loss calculated by Eq. 8. Insertion losses are smaller (more negative) for S2 than for M1 indicating that the pressure amplitudes are larger during S2 than M1. The difference in insertion loss between M1 and S2 is smallest for EMFO, EMFS, and ESLN indicating that QRPmax(first sequence) is closest to QRPmax(second sequence) for these stations (black circles and dotted line in Fig. 10c). This corresponds to the simulated QRPmax ratio where EMFO, EMFS, and ESLN are the largest ratios (still less than one) as observed in Fig. 7 b.

Fig. 10
figure 10

Maximum simulated pressure for M1 (a) and S2 (b) with topography (blue circles) and for a flat plane (red squares). The black line shows 1/R amplitude decay where R is the distance from source to receiver. Insertion loss for each infrasound station for M1 (orange) and S2 (purple) simulations calculated numerically from Eq. 8 following Lacanna and Ripepe (2013) and Maher et al. (2021) (c) and analytically from Eq. 7 using the Maekawa (1968) model (d). Negative insertion loss indicates that the maximum pressure is larger with topography than for the flat plane model. The black circles and dotted line in panel c show the percentage difference between the numerical insertion loss for S2 and M1 on a logarithmic scale (right axis). The insertion loss difference is smallest for EMFO, EMFS, and ESLN

Full size image

There are substantial differences between the numerical (Eq. 8, Fig. 10c) and analytical (Eq. 7, Fig. 10d) results. For the numerical solution, the insertion loss is negative for the majority of stations, indicating that the maximum pressure is larger for the simulation with topography than for the flat plane. For the analytical solution, the insertion loss is always positive indicating that topography causes a loss of amplitude compared to the flat plane case. The differences between Fig. 10 c and d support the results of Maher et al. (2021) and demonstrate that the Maekawa model (1968) is inappropriate for complex volcanic topographies where, as shown in Fig. 10 a and b, topographic focusing can cause substantial increases in amplitude compared to the flat plane case.

Atmospheric effects

We also considered the vertical variation in sound speed on the acoustic wavefield. The effective sound speed is given by:

$${c}_{eff}(z)=c\left(T(z)\right)+v(z)$$
(9)

where z is the height above sea level, T is the atmospheric temperature, and v is the horizontal wind velocity component in the direction of acoustic propagation. We examined the impact of a vertically variable temperature profile.

The temperature profiles were obtained from the spatial interpolation of the vertical profiles of the meteorological data provided by the HydroMeteorological Service of the Emilia-Romagna Regional Agency for Environmental Protection (ARPA-SIM) in northern Italy. These provide GRIB (GRIdded Binary) files packed in a binary format to increase storage efficiency. ARPA-SIM GRIB files are produced using the Cosmo model and are provided every 12 h with a time step of 1 h and the weather forecasts are given until 72 h. The ARPA-SIM grid covers an area rotated with respect to the Equator that is moved to the medium latitudes. It spans from 11.02° to 19.50° E and from 33.96° to 41.02° N and has 14 isobaric levels. The GRIB files are formed from 141×166 points stepped by 0.045°. In particular, we considered the nodes corresponding to the locations of the SEC and the stations EMFO, ESLN, and ESVO. The profiles in the different locations are very similar to each other, so we considered the temperature profile at the SEC. Then, we calculated two median temperature profiles for the lava fountain episodes belonging to the first and second sequences. By using these temperature profiles, we computed the median sound speed profiles for the first and second sequences for the bottom 4000 m of the atmosphere that are included in our modeling (Fig. S6a).

We performed a simulation with the variable sound speed for the first sequence (blue line in Fig. S6a) based on the observed atmospheric temperature profile. We calculated the percentage change in QRPmax between this simulation and the one with the constant sound speed, considering the same topography and source location (Fig. S6b-d). This is shown with the orange triangles in Fig. S6d. The maximum percentage change is less than 20% for all stations. We also calculated the percentage change in QRPmax comparing the results obtained by the simulation M1 and S2 (constant sound speed but varying topography/source location). This is shown with blue circles in Fig. S6d. The maximum percentage change is about 600% and the minimum change is slightly lower than 30%. Overall, the percentage changes are much greater for the topography/source location than for the sound speed.

Because infrasound propagation also depends on local wind conditions and stations located in the downwind direction record larger amplitudes than the stations in the upwind direction (de Groot-Hedlin et al. 2008, 2010; Gainville et al. 2006; Kim et al. 2012), additional analyses were performed using two different datasets. The first dataset of wind of Mt. Etna area (latitude: 37.84; longitude: 15.04; altitude between 1000 m and 3500 m a.s.l.) was provided by ERA5, the fifth generation ECMWF reanalysis for the global climate and weather (https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=overview; Hersbach et al. 2018) (Fig. S7). These data do not show any significant variation between the two eruptive sequences that could be responsible for the observed temporal and spatial variability of the acoustic amplitude. Furthermore, the GRIB files, used to calculate the vertical variation in sound speed due to the changes in temperature, also contain information on the vertical profile of the horizontal wind speed during each lava fountain. Also in this case, the profiles in the four different locations are very similar to each other; hence, the wind profile at the SEC is considered (Fig. 11). The prevailing wind direction is from the north-west to the south-east (as shown in Fig. S7) with wind speeds reaching their maximum value 10 to 15 km above sea level. The data are noisy with no clear differences between the two eruptive sequences. Figure 11b, d shows the mean wind speeds during the first and second sequences. The wind blows less strongly to the south during the second sequence (Fig. 11b), which would suggest lower pressure amplitudes and higher QRP ratios to the South of the vent. This is observed at stations EMFS and ESLN (Fig. 7a). The wind is stronger towards the east in the second sequence (Fig. 11d), which would suggest higher pressure amplitudes and hence lower QRP ratios. However, the observed QRP ratios are higher to the east (e.g., station EMFO; Fig. 7a).

Fig. 11
figure 11

Vertical and temporal variation in horizontal wind speed in South to North direction (a) and West to East direction (c). The red dots indicate the variation over time of QRPcum for ECPN station (a) and EMFO station (c). Positive wind speeds correspond to movement to the North and East. The mean wind speed profile for sequence one (blue) and sequence two (red) are shown in the South to North direction (b) and West to East direction (d). The vertical black lines in (a) and (c) indicate the transition between sequence 1 and 2

Full size image

Discussion

Strong temporal and spatial variability of the acoustic radiation at Mt. Etna during the two eruptive sequences of 2021 is documented here. Specifically, during the first eruptive sequence, stations located on the southern and eastern flanks of the volcano (EMFS, ESLN and EMFO) showed higher QRPcum and QRPmax values compared to the second sequence (Fig. 5).

The acoustic amplitude depends on numerous factors that can mainly be grouped into source and propagation effects. Focusing on source effects, it has been shown that complex source mechanisms (dipole, multipole, or jet noise) have anisotropic radiation patterns (e.g., Woulff and McGetchin 1976; Kim et al. 2012; Matoza et al. 2013; Iezzi et al. 2019; Watson et al. 2021; Iezzi et al. 2022). However, a similar spatial variation, at least in relative terms (the NW stations with higher amplitude values during the second sequence compared to the SE stations), is well reproduced by the numerical simulations (Fig. 7a, b) that used an isotropic source mechanism. Furthermore, while variations in source mechanism and radiation pattern are expected between individual lava fountains, we average over 17 lava fountains in the first sequence and 40 in the second sequence in order to minimize this variation. Hence, although we cannot exclude that complex acoustic source mechanisms, as expected during lava fountain activities, contribute to the anisotropic distribution of the acoustic wavefield, we infer that the source effects are not likely to be the main cause of the observed temporal and spatial variability of the acoustic amplitudes.

The two UAS surveys performed during the first and second eruptive sequences (on 3 March and 16 September 2021) illustrate how the near-vent topography changed during the eruptive sequence (Fig. 2). The 16 September survey shows the accumulation of approximately 90 m of volcanic products near the first sequence vent location. Similarly, more than 110 m of volcanic material was emplaced on the south crater rim. On the south-west flank, a funnel-shaped scar 220 m long and 60 m deep formed. This morphological modification is due to the presence of several fractures, which have substantially weakened the south-west flank of the volcano, and to the activity itself that causes continuous ground shaking promoting the collapse of portions of the flank. These two morphological changes contributed to the shift of the vent towards south-west. Such a topographic change affected the observed spatial distribution of the acoustic amplitude. A confirmation of the important role played by the topographic changes derives from the other two numerical simulations performed by exchanging source locations and DSMs and computing all the synthetic QRP ratios (Figs. 6d–g and 7c–f). Among the results of these simulations, the result showing a spatial distribution of the QRP ratio similar to the observed distribution (apart from M1/S2, showing the best match to the data) is the one obtained using a constant source location (the one considered for the second eruptive sequence) and both the DSMs of March and September 2021 (M2/S2; Figs. 6e, 7d, 8a) with a correlation coefficient of 0.92 (compared to 0.96 for M1/S2, Table 1). This similarity suggests that the low acoustic ratios observed at the NW stations (Figs. 6b and 7a), meaning relatively high acoustic amplitudes observed during the second sequence compared to the SE stations, are due to the topographic changes from M to S, together with the acoustic source located in position 2 during the second sequence. The correlation coefficient for M1/S1 is much lower at 0.23 compared to 0.74 for S1/S2. This illustrates that the observed acoustic radiation is a complex combination of topography and source effects, with the dominant factor depending on the specific topography.

Topography is able to modulate the acoustic wavefield in two different and contrasting ways: (i) barriers can produce a shielding effect attenuating the acoustic amplitude; (ii) concave slopes can generate constructive interference giving rise to amplification of the acoustic wavefield. As for the (i), according to the literature (e.g., Lacanna and Ripepe 2013; Ishii et al. 2020; Maher et al. 2021; Khodr et al. 2022), the amount of attenuation due to the barrier depends on several parameters such as the Fresnel number (function of the difference between the diffracted path and the direct path to a receiver, as well as of the signal wavelength), the ratio between the barrier height and the source-receiver distance, and the ratio between the source-receiver distance and the signal wavelength. Concerning (ii), according to Lacanna et al. (2014) and Maher et al. (2021), the correct estimation of the spatial variability of the acoustic amplitudes has to take into account also the possible constructive interferences of multiple reflections along concave volcano slopes that can counteract losses by barrier diffraction. Focusing of acoustic waves is not accounted for in the Maekawa (1968) insertion loss model (Eq. 7) and hence this analytical model overpredicts the attenuation compared to the numerical result (Eq. 8; Fig. 10). For the topography considered here, the analytical model predicts positive insertion loss for all stations (amplitude with topography is less than amplitude for a flat plane, Fig. 10d) whereas the numerical model predicts negative insertion loss (amplitude with topography is more than amplitude for a flat plane) for all stations apart from EPLC and ESVO for M1 (Fig. 10c). For the Maekawa (1968) analytical model, the average insertion loss is 5.7 dB for M1 and 6.4 for S2, which is contrasted with −2.1 dB for M1 and −7.0 dB for S2 for the numerical model (equation 8). These results reinforces the claim of Maher et al. (2021) that the “thin screen approximation proposed by Maekawa (1968) is an inappropriate model for diffraction by volcano topography because attenuation is overestimated in the topography case” and that “true attenuation is smaller than predicted by Maekawa’s empirical relationship because constructive interference of reflections down the concave volcano slopes (focusing) cause amplitude increases that counteract losses by diffraction.”

The spatial distribution of the synthetic acoustic amplitude ratios derived by the main numerical simulation (Figs. 6c and 7b) is similar to that observed in relative terms (correlation coefficient of 0.96, Figs. 6b and 7a), thus confirming how the aforementioned topography-related phenomena are able to strongly modify the spatial distribution of the infrasonic amplitude. It is also evident how the absolute values of the synthetic and observed acoustic amplitude ratios are different (QRP ratios are all greater than 1 for the observations but less than 1 for the M1/S2 simulations). This could be due to the higher acoustic amplitude at the source during the first eruptive sequence compared to the second sequence. The variability of the source acoustic amplitude was not taken into account in the numerical simulations. However, considering a scaling factor for the synthetic signals generated during the second sequence S2 (best-fitting scaling factor α = 0.18), the match is very good for most of the stations—differences are largest for EMFS, EPLC, and EMFO but still within the observation error (Fig. 8b). This means that the acoustic amplitude of the source during the first eruptive sequence is approximately five times higher than during the second sequence.

Combining the topography-related changes and the source amplitude variations, it is evident that the high values of the QRP ratio between the first and second sequence, observed at stations located in the southern and eastern flanks (the ones showing the lowest variations in insertion loss from M1 to S2; Fig. 10c), mostly reflect the decrease in source amplitude inferred for the second sequence. On the other hand, the stations located in the northern and western flanks exhibited the strongest changes in insertion loss, due to high negative values of insertion loss during S2 compared to what was obtained in M1 for these stations. Such a variation causes a strong amplification of the acoustic amplitude during the second sequence at these stations to cancel the effects of the source amplitude decrease, resulting in a QRP ratio between first and second sequence around 1. Although it is clear that the strong negative values of insertion loss obtained at the NW stations should be related to constructive interference of the acoustic wavefield along the concave volcano slopes, it is not trivial to understand why this amplification differs between M1 and S2 so significantly at NW stations. What we can infer by using all the numerical simulation results (Figs. 6 and 7) is that the combination between topography S and source location in 2 in the simulation placed as denominator of the QRP ratio is necessary to get very low values of the such a QRP ratio in the NW stations, meaning high amplification values in the denominator simulation results. However, the exact mechanism leading to such high amplification during the second sequence in this sector of the volcano compared to the first will be explored in a future work.

In addition, according to the results of Fig. S4, we can affirm that the variation in QRP ratio during the second sequence is not gradual but sudden; in fact, although the topography gradually changes, at the beginning of the second sequence the source location abruptly shifted of about 200 m towards SW.

The small differences between the results of the simulations and the observed data could be due to source anisotropy. Indeed, in the simulations, a simple monopole source, radiating acoustic waves equally in all directions, is considered, while the acoustic source during lava fountains is expected to be anisotropic (Matoza et al. 2013). Other factors to consider include the following: the simulations assume a simple point source explosion that lasts for ~1 s, while the real source mechanisms are complex lava fountain episodes that last for multiple hours; the possibility of under-resolved topography in the near vent region, either due to down-sampling to 18-m resolution in the simulations or the limits of the topographic survey; the data is averaged over multiple events whereas the simulations are for a single event; for the simulations, only two snapshots of the topography at different points in time were used whereas the topography could been changing continuously throughout the eruptive sequence, especially in the SEC region. Furthermore, also the possible upward refraction from the atmospheric boundary layers were not accounted for in this paper. These effects could contribute to explain the differences between synthetic and observed acoustic amplitude ratios. Despite the limitations with the simulations, the good agreement between the simulations and data suggests that topography and changing source location (in addition to the changing source amplitude) are important factors in controlling the observed infrasound amplitude.

Local infrasound observations also depend on variations in sound speed due to the temperature and local wind conditions (Johnson 2019) with higher amplitudes observed in the downwind direction. Fig. S6d shows that the percentage change in QRPmax in the case of changing topography and source location is greater than that in the case of changing sound speed profiles. Hence, we argue that the change in topography and source location has more impact on the observed infrasound signal than the variation in sound speed due to temperature changes. Wind speeds are shown in Figs. 11 and S7 and do not show substantial changes between the two sequences. Furthermore, the observed slight changes in the wind speed do not match the changes in the infrasound observations. The QRPmax ratios are higher at EMFO, EMFS, and ESLN the south and east of the vent (Fig. 7a), indicating that the pressure during the second eruptive sequence at these stations is relatively less than at the stations to the north and west. These findings are consistent with Fig. 11b, which shows that the winds are less strong to the south during the second sequence, which would suggest higher pressure amplitudes to the north. However, Fig. 11d shows that the winds are more strongly to the east during the second sequence, which would suggest lower pressure amplitudes to the west. This conflicting evidence suggests that local wind conditions are not the dominant factor controlling the temporal and spatial variation in infrasound radiation pattern in this instance. Future work could use a ray-tracing method to quantify the effect of variations in local wind conditions on the observed infrasound signal (Bowman and Krishnamoorthy 2021; De Negri and Matoza 2023).

Conclusions

This work demonstrates how the time variation of acoustic amplitudes during eruptive phenomena could be due not only to modifications in source parameters such as mass eruption rate, flow rate, and source depth but also to shifts (even very slight) in the source position and changes in topography, particularly in the near-vent region. This is particularly important for long-duration eruptive sequences that last for multiple weeks or months. Changes in topography and source location, which can be rapid and frequent at very active volcanoes as Mt. Etna, are able to strongly modify the acoustic wavefield. Hence, to reliably monitor the volcanoes through acoustic signals and their changes over time, accurate and up-to-date topographic information plays a very important role along with well-constrained source locations. In particular, UASs can produce high-resolution topographic surveys but can only fly when weather conditions allow and volcanic activity is low, permitting pilots to safely get close to vents to fly those UASs. This stresses the importance of high-resolution satellite-derived topographic observations and longer-range UASs that can fly into hazardous areas to get updated topography in near real time.