Evidence for near-source nonlinear propagation of volcano infrasound from Strombolian explosions at Yasur Volcano, Vanuatu

Abstract

Volcanic eruption source parameters may be estimated from acoustic pressure recordings dominant at infrasonic frequencies (< 20 Hz), yet uncertainties may be high due in part to poorly understood propagation dynamics. Linear acoustic propagation of volcano infrasound is commonly assumed, but nonlinear processes such as wave steepening may distort waveforms and obscure the sourcing process in recorded waveforms. Here we use a previously developed frequency-domain nonlinearity indicator to quantify spectral changes due to nonlinear propagation primarily in 80 signals from explosions at Yasur Volcano, Vanuatu. We find evidence for $\le$ 10⁻³ dB/m spectral energy transfer in the band 3–9 Hz for signals with amplitude on the order of several hundred Pa at 200–400 m range. The clarity of the nonlinear spectral signature increases with waveform amplitude, suggesting stronger nonlinear changes for greater source pressures. We observe similar results in application to synthetics generated through finite-difference wavefield simulations of nonlinear propagation, although limitations of the model complicate direct comparison to the observations. Our results provide quantitative evidence for nonlinear propagation that confirms previous interpretations made on the basis of qualitative observations of asymmetric waveforms.

Introduction

Volcanic eruptions produce acoustic waves dominant at infrasonic frequencies (< 20 Hz) that are increasingly studied in both research and monitoring contexts due to their usefulness in detecting, locating, and characterizing eruptive activity (e.g., De Angelis et al. 2019; Johnson 2019; Matoza et al. 2019). At local recording distances (< 15 km), infrasound has been used in attempts to make quantitative estimates of eruption source parameters such as vent and crater geometry (e.g., Johnson et al. 2018; Muramatsu et al. 2018; Watson et al. 2019), mass and volume flux (e.g., Moran et al. 2008; Johnson and Miller 2014; Kim et al. 2015; Fee et al. 2017), and plume height (e.g., Caplan-Auerbach et al. 2010; Ripepe et al. 2013; Lamb et al. 2015). These estimates have largely been made assuming linearity in the acoustic source process and during wave propagation (De Angelis et al. 2019), yet significant nonlinear dynamics are expected near the source (e.g., Morrissey and Chouet 1997; Yokoo and Ishihara 2007; Marchetti et al. 2013). Acoustic wavefields may be modulated at the source by processes such as fluid flow and jet turbulence (e.g., Matoza et al. 2009, 2013; Taddeucci et al. 2014; Watson et al. 2021) and during propagation by wave steepening and period lengthening (e.g., Hamilton and Blackstock 2008; Marchetti et al. 2013; Maher et al. 2020). These processes may distort the waveforms and frequency content of observed signals, causing inaccurate interpretation of the source mechanism when linear generation and propagation are assumed (Maher et al. 2020; Watson et al. 2021). An improved understanding of nonlinear dynamics is therefore needed to reduce uncertainty in the infrasound-based estimation of source parameters; here, we focus on nonlinear propagation.

Nonlinear propagation occurs when the applied pressure is significant compared to the ambient pressure, causing local changes in particle velocities and temperatures (Atchley 2005; Hamilton and Blackstock 2008). In this case, the sound speed becomes pressure dependent such that higher amplitude and compressional portions of the wave travel faster than lower-amplitude and rarefaction portions (Hamilton and Blackstock 2008). This differential speed causes the wavefield to steepen toward a shock wave, which is a pressure discontinuity where the point of peak pressure overtakes the wave onset (Hamilton and Blackstock 2008). Wave steepening in the time domain may be correlated with positive skewness of pressure and the first-time derivative of pressure, although these statistical analyses require large sampling rates and high signal-to-noise ratios (McInerny et al. 2006; Gee et al. 2013; Reichman et al. 2016b). In the frequency domain, wave steepening corresponds to spectral energy transfer: energy is lost from the dominant frequency components and gained at successively higher harmonics (Hamilton and Blackstock 2008). Energy may also be transferred to lower frequencies (period lengthening) once wave steepening has generated an N-wave, but this process is less efficient than upward energy transfer because the front and leading edges of the wave must be shock-like (Hamilton and Blackstock 2008). A consequence of these phenomena is that nonlinearly propagated volcano acoustic signals may be richer in high-frequency content and lower in peak pressure than expected for an equivalent source pressure based on linear acoustic theory (Morfey and Howell 1981; Hamilton and Blackstock 2008).

Although nonlinear propagation of volcano infrasound has long been suspected and cited as a source of uncertainty (e.g., Morrissey and Chouet 1997; Garcés et al. 2013), quantification of the nonlinear processes remains challenging. Asymmetric waveforms (large-amplitude short-duration compression phases followed by longer lower-amplitude rarefaction phases) have been interpreted as possible evidence of nonlinear sources and/or propagation (Fee et al. 2013; Marchetti et al. 2013; Goto et al. 2014; Anderson et al. 2018; Matoza and Fee 2018; Matoza et al. 2018), but they have also been explained in terms of crater rim diffraction (Kim and Lees 2011) and fluid flow at the source (Brogi et al. 2018; Watson et al. 2021). Similarly, visual observations of luminance changes corresponding to the passage of volcano-acoustic waves through water vapor have been interpreted as evidence of supersonic (nonlinear) propagation (Ishihara 1985; Yokoo and Ishihara 2007; Marchetti et al. 2013). However, the estimates of wavefront velocity are not always supersonic (Genco et al. 2014), and uncertainty ranges on the estimates do not rule out ambient (sonic) propagation speeds. Nonlinear propagation may still occur at sonic propagation speeds if shocks are balanced across zero dynamic pressure, such as for sawtooth waveforms (Hamilton and Blackstock 2008).

Several quantitative models for nonlinear infrasound propagation have recently been proposed. Dragoni and Santoro (2020) provided analytical relationships for shock wave properties, including pressure with distance from the source; however, these are valid for strong shocks (pressures greater than six times atmospheric pressure, or > 607,800 Pa at sea level), which are larger in amplitude than observed signals (up to 1200 Pa at 2 km; Anderson et al. 2018). Watson et al. (2021) performed aeroacoustic simulations that illustrate nonlinear waveform steepening and how erupted volumes are underestimated when linear propagation is assumed. Maher et al. (2020) applied a quantitative indicator of nonlinearity (developed by Reichman et al. 2016a) to data and synthetics corresponding to explosion signals at Sakurajima Volcano, Japan. Their results from numerical modeling suggested that the indicator could quantify several decibels of spectral energy transfer at Sakurajima explosion amplitudes, but applications to the observed data were complicated by additional outdoor propagation dynamics (e.g., refraction in wind gradients and topographic scattering). Topographic scattering was shown to dominate the distortion of the waveform, but nonlinear spectral energy transfer was found to be an important secondary process (Maher et al. 2020).

In this study, we extend the work of Maher et al. (2020) by applying a quantitative nonlinearity indicator to infrasound signals from explosions at Yasur Volcano, Vanuatu. While the analysis at Sakurajima (Maher et al. 2020) was complicated by complex topography and few stations with wide azimuthal coverage, a 2016 field campaign at Yasur (Jolly et al. 2017; Matoza et al. 2017, 2022; Iezzi et al. 2019) affords detailed study of the near-source wavefield (0.2–1 km). The topography in the Yasur deployment is relatively minimal compared to volcanoes such as Sakurajima, where the wavefield interacts with multiple topographic barriers such as ridges and valleys, although complexity may still be introduced by topography in the crater and around the crater rim. The infrasound deployment included 15 receivers, including two to three sensors aboard a tethered aerostat and a six-element radial line array, enabling observation of wavefield changes with distance and height (Jolly et al. 2017; Matoza et al. 2017). We primarily apply the indicator to signals from 80 explosions and to synthetics generated from two-dimensional (2D) axisymmetric finite-difference modeling of nonlinear infrasound propagation (de Groot-Hedlin 2012, 2017). We also consider 2068 events as recorded at a single station over a 2-day period to investigate changes through time, and we estimate potential errors in source volume estimates due to the nonlinear propagation effects.

Quadspectral density nonlinearity indicator

Although nonlinear acoustic propagation is a well-understood phenomenon from a theoretical perspective (Hamilton and Blackstock 2008), it is not straightforward to identify in recorded waveforms. Various methods have been proposed as indicators of nonlinearity, especially in studies of man-made jet noise signals at audible frequencies (20–20,000 Hz), such as the skewness of the waveform and its derivative (McInerny and Ölçmen 2005; Gee et al. 2013), bicoherence (Kim and Powers 1979; Gee et al. 2010), and quadspectral density (Morfey and Howell 1981; Petitjean et al. 2006; Pineau and Bogey 2021). Similarities in power spectra have been observed between volcano infrasound and man-made jet noise, leading to the hypothesis that both types of signals are created by similar processes (turbulence and shearing between ambient air and a momentum-driven fluid flow) (Matoza et al. 2009). As a result, methods designed for indicating nonlinearity in jet noise at audible frequencies, such as skewness, have found novel applications to volcanic signals at infrasonic frequencies (< 20 Hz) (e.g., Fee et al. 2013; Anderson et al. 2018). These approaches effectively yield proxies for nonlinearity without direct physical interpretation; for example, positive values of waveform derivative skewness indicate steep compressional onsets that may then be interpreted as shock fronts (e.g., Muhlestein and Gee 2011; Shepherd et al. 2011). Recently a quantitative quadspectrum-based indicator (ν_N) was developed, which gives the rate of change in spectral level (unit dB/m) at a single point due to nonlinear propagation processes (Reichman et al. 2016a). The method has been shown to yield results consistent with nonlinear acoustic theory for supersonic model-scale jet noise (Miller and Gee 2018) and full-scale military aircraft noise (Gee et al. 2018). Maher et al. (2020) were the first to apply ν_N to infrasonic frequencies and volcano acoustic data, using explosion signals from Sakurajima Volcano as a case study.

The ν_N indicator constitutes the nonlinear term of a frequency domain form of the generalized Burgers equation adapted by Reichman et al. (2016a) following work by Morfey and Howell (1981). This equation describes the spatial rate of change in a wave’s sound pressure level (L_p) due to geometrical spreading (ν_S), absorption (ν_α), and finite amplitude effects (ν_N):

$$\begin{array}{c}\frac{\partial {L}_{p}}{\partial r}= -10{\mathrm{log}}_{10}\left(e\right)\times \left(\frac{2m}{r}+2\alpha + \frac{\omega \beta }{{\rho }_{0}{c}_{0}^{3}}\frac{{Q}_{{pp}^{2}}}{{S}_{pp}}\right)\\ \equiv {\nu }_{S} + {\nu }_{\alpha } + {\nu }_{N},\end{array}$$

(1)

where $\frac{\partial {L}_{p}}{\partial r}= \nu$ is the dB/m rate of change in distance (r) of the sound pressure level:

$${L}_{p} = 10{\mathrm{log}}_{10}\frac{{p}_{i}}{{p}_{ref}^{2}},$$

(2)

where p_i is power spectral density in an arbitrary frequency band and p_ref is a reference pressure (here 20 µPa). The term m is a nondimensional geometrical spreading term equal to 0, 0.5, or 1 for planar, cylindrical, or spherical waves, respectively, and α is the frequency-dependent absorption coefficient of the medium. We are interested in the nonlinear term:

$${\nu }_{N} = -10{\mathrm{log}}_{10}\left(e\right)\times \left(\frac{\omega \beta }{{\rho }_{0}{c}_{0}^{3}}\frac{{Q}_{{pp}^{2}}}{{S}_{pp}}\right),$$

(3)

where e ≈ 2.718, ω is the angular frequency, β is the medium’s coefficient of nonlinearity, ρ₀ is ambient density, c₀ is ambient sound speed, and Q_pp2 is the quadspectral density (imaginary part of the cross-spectral density) of the waveform p and its square p², and S_pp is power spectral density (PSD) of the waveform. The nonlinearity coefficient β is a unitless constant that characterizes the effect of finite-amplitude wave propagation on sound speed; in the air $\beta \approx 1.2$ (Hamilton and Blackstock 2008). The quadspectrum Q_pp2 reflects phase coupling between frequency components that arises during nonlinear spectral energy transfer (Kim and Powers 1979; Gagnon 2011). The ν_N indicator quantifies the rate of spectral energy transfer (dB/m) at the measurement point, giving negative values at frequencies where energy is lost and positive values at frequencies where energy is gained.

The applicable frequency range of ν_N depends on sample rate (Fs) and recording distance (r). The theoretical upper-frequency limit is Fs/4 because Q_pp2 compares the waveform and its square, and squaring the waveform doubles its frequency components. The square of the Fs/4 component is, therefore, compared to the Nyquist frequency, and higher frequencies are not constrained. The lower frequency must satisfy the quasi-plane wave assumption of the GBE that kr >  > 1 (Hamilton and Blackstock 2008), where k is the angular wavenumber (k = 2πf/c). We limit our analysis to frequencies where kr > 10, which for c = 346 m/s and 200 ≤ r ≤ 1000 m corresponds to lower limits of 0.6–2.8 Hz depending on the source vent and receiver. Miller and Gee (2018) used kr > 29 in their analysis, but they observed significant spectral changes with distance due to source directivity of their model-scale jet (independent of nonlinear propagation) and therefore needed greater distances to avoid the near-field for low frequencies. At Yasur Volcano, the explosions are well-modeled by a monopole source (Iezzi et al. 2019), for which all frequency components are generated at the same location. Use of kr > 29 at Yasur Volcano would produce minimum frequency limits of 1.5–6.9 Hz and cut into a relevant band for ν_N analysis surrounding and immediately above the dominant frequencies (∼1–10 Hz). We, therefore, consider a lower kr > 10 thresholds appropriate.

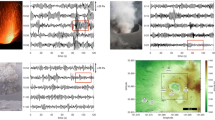
The expected behavior of ν_N for various signal types is illustrated in Fig. 1. Figure 1a shows an example waveform for sustained jet noise generated by a model scale jet with supersonic exit velocities, Fig. 1b shows the power spectra for several of these waveforms recorded at different distances, and Fig. 1c shows the corresponding ν_N results (data from Miller and Gee 2018). The analysis reveals negative ν_N values at frequencies just above the dominant observed frequency range of 3–10 kHz and positive values at higher frequencies (> 20 kHz). Maher et al. (2020) referred to this signature as a reclined S-shape that indicates upward spectral energy transfer, i.e., power is lost in the dominant frequency range of the sourcing process and transferred to higher harmonics. These data from Miller and Gee (2018) represent nonlinear propagation; results for linear propagation can be approximated by generating white noise waveforms sampled from normal distributions with the same means and standard deviations as the observed jet noise. Figure 1d shows an example of this corresponding to the jet noise in Fig. 1a, Fig. 1e shows the corresponding power spectra for each white noise waveform, and Fig. 1f shows the ν_N results. Clearly, for linear propagation, the ν_N magnitudes are reduced, and the reclined S-shape does not appear. Finally, in Figs. 1g–I, results are shown for a short-duration impulsive waveform representing the shock wave from an exploding oxyacetelyne balloon (data from Young et al. 2015). These results show that the expected reclined S-shape of ν_N is observed for impulsive nonlinear signal types in addition to sustained noise.

Fig. 1

Waveforms (a, d, g), power spectra (b, e, h) and ν_N results (c, f, i) for supersonic model scale jet noise (a, b, c), numerically generated white noise (d, e, f) and an exploding oxyacetelyne balloon (g, h, i). Model scale jet noise data are from Miller and Gee (2018) and the distances are scaled by jet diameter (D_j = 0.035 m). Waveforms in 1a and 1d correspond to 75 D_j. Exploding balloon data are from Young et al. (2015) and were recorded at 76.2 m distance and 0.9 m above the ground

While the examples shown in Fig. 1 demonstrate expected ν_N behavior for audible frequency acoustics (20 Hz–20 kHz), the method was previously validated for infrasonic frequencies in numerical simulations of volcano infrasound (Maher et al. 2020). The expected reclined S-shape was observed in results from synthetic waveforms generated by numerical modeling of nonlinear infrasound propagation, but not for observed signals from Sakurajima Volcano (Maher et al. 2020). These findings suggest that propagation nonlinearity is potentially observable with ν_N at the amplitudes observed at Sakurajima, but complicating factors in outdoor propagation (e.g., refraction, diffraction, and reflections) obscured its signature in ν_N. We hypothesize that ν_N is better able to quantify nonlinearity in Yasur Volcano explosion signals due to close source-receiver distances and less obstructive topography.

Yasur volcano and dataset

Background

Yasur volcano is a basaltic-andesitic cone of lava and pyroclastic deposits on the island of Tanna in the Vanuatu Archipelago of the South Pacific (Fig. 2). The volcano has produced consistent eruption activity for the past 800 years (Firth et al. 2014), with near-continuous gas emissions and up to several explosions occurring every minute (Métrich et al. 2011; Vergniolle and Métrich 2016). The eruptions are primarily Strombolian, and mildly Vulcanian activity is only rarely observed (Firth et al. 2014). Infrasound from the explosions is regularly detected 400 km away and has been used to probe seasonal changes in atmospheric structure (Le Pichon et al. 2005). The persistent eruptions and the approachability of the crater rim have made Yasur a research target for open-vent systems, with studies in recent years examining activity with visual, ultraviolet and thermal imaging, seismicity, infrasound, and Doppler radar (e.g., Kremers et al. 2013; Marchetti et al. 2013; Battaglia et al. 2016; Spina et al. 2016; Meier et al. 2016; Jolly et al. 2017; Iezzi et al. 2019; Fitzgerald et al. 2020; Simons et al. 2020; Fee et al. 2021; Matoza et al. 2022).

Fig. 2

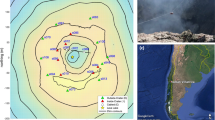
Map of the Yasur Volcano during the July–August 2016 deployment using a 2 m resolution digital elevation model (for details, see Iezzi et al. 2019) and 50 m contours. Downward triangles indicate ground-based infrasound stations, and circles represent aerostat locations during the 80 events studied here. The active north and south vents are indicated by black triangles. The dashed line corresponds to the topographic profile at the lower right. Inset globe shows the volcano location (black triangle) on Tanna Island in the Vanuatu archipelago

The edifice consists of a roughly 400 m wide crater with a maximum rim elevation of ∼360 m above sea level, steep slopes to the north and west, and a level ash plain to the south and east (Fig. 2). In 2016 the crater hosted three active vents in two sub-craters separated by a low barrier; these vents have been termed, from south to north, vents A and B in the south crater and vent C in the north crater (Oppenheimer et al. 2006). Vent A typically produces more frequent and violent explosions than vent B (e.g., Marchetti et al. 2013; Iezzi et al. 2019; Simons et al. 2020), and the separation between the two vents are small (∼20–40 m; Simons et al. 2020). Additionally, explosion sources from reverse time migration cluster in only one location in the south crater rather than two (Fee et al. 2021). We, therefore, simplify our terminology to consider the source locations as north crater and south crater, with the understanding that high-amplitude signals from the south crater are likely to arise from explosions at vent A (Jolly et al. 2017; Matoza et al. 2022). We use a 2 m resolution digital elevation model (DEM) previously developed by Iezzi et al. (2019), which combines ASTER Global and Worldview02 DEMS far from the crater with a higher-resolution DEM of the crater area created with data from an unmanned aerial vehicle and structure-from-motion methods (Fitzgerald 2019).

Infrasound deployment and dataset

In July and August 2016, a field campaign at Yasur Volcano was conducted by researchers at the University of California Santa Barbara, University of Alaska Fairbanks, GNS Science New Zealand, University of Canterbury, and the Vanuatu Meteorology and Geohazards Department (Jolly et al. 2017; Matoza et al. 2017, 2022; Iezzi et al. 2019; Fitzgerald et al. 2020; Fee et al. 2021). The infrasound deployment included six ground-based sensors around the crater rim (YIF1–YIF6), six ground-based sensors arranged in a line radiating 180° azimuth from the south crater (YIB11–YIB23), and three sensors suspended from an aerostat around the crater rim (YBAL1–3) (Fig. 2). Sensors YIF1 and YIB11–YIB23 did not have direct lines of sight to the vents due to the intervening crater rim. The ground-based sensors are Chaparral Physics Model 60 UHP with a ± 1000 Pa pressure range and flat response between 33 s and Nyquist. The aerostat sensors are InfraBSU type and have flat responses from 30 s to Nyquist. All data were digitized with Omnirecs DATA-CUBE digitizers. Ground-based sensors were sampled at 400 Hz, while aerostat sensors were sampled at 200 Hz. All ground-based sensors except YIF6.1 collected data from July 27 to 1 August 1, while some elements of the line array (YIB*) were operational on July 26 and August 2. Station YIF6 only collected data on July 28–29 and is excluded from this study.

The aerostat was floated between 30 and 100 m above the local topography with three sensors hung from a string at 10 m vertical spacing below the balloon. The bottom of the string was weighted with a digitizer and on-board GPS unit, giving location estimates with errors approximated at 10 m laterally and 15 m vertically (Jolly et al. 2017). The aerostat was moved every 15–60 min to 38 loiter positions around the north to southeast crater rim during daylight hours from July 29 to August 1 (for details, see Jolly et al. 2017).

Volcanic activity during the study period was nearly continuous with persistent degassing and explosions every ∼1 to 4 min. Jolly et al. (2017) used continuous phase lag processing between stations YIF1 and YIF4 to distinguish the dominant crater activity in 20 s time windows, finding 2132 windows that favored the south crater and 859 windows that favored the north crater. Fee et al. (2021) applied a new technique they term reverse time migration-finite-difference time-domain (RTM-FDTD) to 12 h of data on July 28–29, 2016 and identified 1589 events during this interval alone, with the majority relocating in clusters close to vent A (south crater) and vent C (north crater). Beginning on July 31, the activity increased in intensity and shifted from predominantly the north crater to the south crater (Jolly et al. 2017; Iezzi et al. 2019; Fitzgerald et al. 2020; Matoza et al. 2022). Iezzi et al. (2019) used STA/LTA detection on an aerostat sensor during time periods when the aerostat was tethered and with good constraints on its geographic location. They identified 201 impulsive events and used the relative arrival times at crater rim stations to distinguish between north and south vents. They then chose 40 events from each crater with a wide range in aerostat positions to invert for a multipole source mechanism and minimum residual source location. We primarily focus on the 80 events analyzed by Iezzi et al. (2019) because they feature good constraints on source location and aerostat position.

Observational results

To test for evidence of nonlinear propagation, we apply the ν_N indicator to data from all available sensors during each of the 80 explosive events analyzed by Iezzi et al. (2019). We use a multitaper method (Riedel and Sidorenko 1995) to estimate power spectra and cross spectra for p and p² in 20 s time windows centered on peak pressure at each sensor. Prior to spectral estimation, the waveforms are detrended and tapered with a 40% Tukey window. The Tukey window tapers a percentage of the edges of the series while leaving the center unaffected; a 0% shape factor represents a boxcar function while 100% is equivalent to a Hann function. We then smooth the power spectra and quadspectra using a locally weighted least squares method. This smoothing method allows users to control the percentage of input points fit in each window for least-squares smoothing; we choose 0.9% to reduce variance at high frequencies while preserving resolution at low frequencies. Finally, we estimate the PSD at all stations during a 2 min period without explosions due to relatively lower activity (July 31, 01:47:30–01:49:30) and average across the different sensor groups (crater rim, line array, and aerostat) to compare signals to noise as a function of frequency. We avoid interpreting ν_N at frequencies for which the signal-to-noise ratio (SNR) of power spectra in-unit Pa²/Hz is less than six.

When calculating ν_N, we assume c₀ = 346 m/s, ρ₀ = 1.18 kg/m³, corresponding to a representative air temperature value of 25 °C observed during the campaign (Iezzi et al. 2019), and β = 1.201 (Hamilton and Blackstock 2008). We present ν_N results directly in unit dB/m rather than integrating with respect to distance, as done by Maher et al. (2020). They assumed a constant rate of change with distance to obtain a cumulative estimate of the nonlinear changes (ν_Ntot); however, the rate is unlikely to be constant. Nonlinear changes increase with amplitude and thus proximity to the source and the behavior of each frequency component changes with distance as spectral energy is transferred.

Figure 3 shows an example set of waveforms, power spectra, and ν_N results for a single event in the south crater as recorded at all stations. For ease of viewing the results are grouped in three columns by sensor sets (aerostat, crater rim, and line array). The waveforms are generally asymmetric at the aerostat (Fig. 3a) and line array sensors (Fig. 3c) with a high-amplitude compressional onset followed by a lower amplitude rarefaction phase. The waveforms at the crater rim are more symmetric (Fig. 3b), suggesting a possible focalization effect whereby the wavefield is distorted by topography (Kim and Lees 2011; Lacanna and Ripepe 2020). The power spectra (Fig. 3d–f) show peak power around 2–3 Hz at the aerostat and crater rim stations that appears to move to lower frequencies (∼1 Hz) at the line array. The ν_N spectra (Fig. 3g–i) show the characteristic reclined S-shape between ∼3 and 8 Hz indicating 10⁻⁴ to 10⁻³ dB/m upward spectral energy from ∼5 to 7 Hz. At frequencies higher than 10 Hz, the variance in ν_N becomes too high to discern true nonlinear features, and at the line array, ν_N is screened by the SNR above 40 Hz. Note that at the aerostat and some crater rim stations, the lower frequencies (< 3 Hz) are not shown where kr < 10 (see “Quadspectral density nonlinearity indicator” section for details).

Fig. 3

a–c Waveforms, d–f PSD curves, and g–i) ν_N results for a single event at 03:21:59.42 on August 1, 2016 (UTC). Waveforms and spectra are grouped by aerostat sensors (first column), crater rim sensors (second column), and line array (third column). Waveform amplitudes are normalized by the maximum (p_max) at the top-most sensor in each group (e.g., by YBAL3 in 3a). Dashed black “noise” curves in 3d–i show spectra at one sensor in each group during a quiet period of ambient noise. Light gray ν_N curves in g–i indicate frequencies for which SNR ≤ 6.

While Fig. 3 shows one event at all stations, Fig. 4 shows ν_N results for all events at three stations with increasing distance from the craters: YIF4 on the crater rim (Fig. 4a), YIB21 on the near side of the line array (Fig. 4b) and YIB13 on the far side of the line array (Fig. 4c). In this figure, the smoothing parameter is increased to 2.5% to emphasize the dominant trend. Spectra are colored by the peak pressure in the corresponding waveform at YIB21 such that each event has the same color at each station shown. In general, the magnitude of ν_N increases with peak pressure and decreases with receiver distance as expected, since nonlinearity increases with amplitude (note that the scale is 10⁻³ dB/m for YIF4 vs 10⁻⁴ for YIB21 and YIB13). Conversely, the stability of the ν_N shape generally increases with receiver distance, e.g., at YIB13 ν_N, features consistent troughs at 4–6.5 Hz and peaks at 7–9 Hz, whereas at YIF4, these structures occur over broader and less consistent frequency ranges. Thus, the ν_N signature becomes clearer as a function of waveform amplitude and receiver distance for the cases considered here.

Fig. 4

Spectra of ν_N in the frequency range 3–9 Hz for south vent events recorded at a YIF4, b YIB21, and c YIB13, and for north vent events recorded at d YIF4, e YIB21, and f YIB13. Spectra are smoothed in 2% bands and colored by peak waveform pressure (p_max) at YIB21. Results are only plotted at frequencies where SNR > 6 and kr > 10

Numerical modeling

To further investigate possible topographic effects on the ability to recover nonlinearity in the Yasur Volcano explosion waves, we applied ν_N to synthetic pressure waveforms generated by numerical wavefield modeling that allows for nonlinear propagation and topography. We hypothesize that if the observed ν_N features (e.g., Figs. 3g–i) are caused by nonlinear propagation, then they should be closely reproduced by synthetics when comparable pressure amplitudes (∼250 Pa at ∼400 m) and frequencies (∼3–8 Hz) are simulated.

Finite-difference method

We ran numerical wavefield simulations using a finite-difference time-domain (FDTD) method for nonlinear infrasound propagation developed by de Groot-Hedlin (2012, 2017). The method solves the Navier–Stokes equations with second-order accuracy in the space and time derivatives (de Groot-Hedlin 2012, 2017). This method was previously used to investigate the effects of nonlinearity (Maher et al. 2020) and topographic diffraction (Maher et al. 2021) on explosion signals at Sakurajima Volcano, Japan. The simulations are run in a cylindrical coordinate system with an axisymmetric geometry about the left boundary, allowing for modeling of spherical spreading in a 2D source-receiver plane. The model includes rigid stair-step topography at the lower boundary and absorbing perfectly matched layers at the top and right boundaries (Berenger 1994). The source is initialized as a spatially distributed Gaussian pulse centered at the lower-left corner of the model space at time zero, requiring a flat topographic area within the source region. To accommodate this, we add an artificial 175 m wide flat area to the left side of each topographic profile at the elevation of the crater floor (e.g., see Fig. 5a). This configuration is required for numerical stability and precludes alteration of the source without significant modification to the method. This limitation means that we cannot manipulate the source-time function to minimize waveform residuals and are limited to reproducing comparable peak amplitudes.

Fig. 5

Synthetic wavefields at a t = 0 s over YIF1 topography, b t = 1.5 s over YIF3 topography, c t = 2.3 s over YIF5 topography, d t = 4.6 over YIF4 topography, and e comparison of synthetic waveforms (black) to observed (color) at aerostat and rim stations for an event at 04:53:12.87 on August 1, 2016. Amplitudes are normalized by maximum pressure at synthetic YBAL3 (p_max). Observed waveform times are matched by peak pressure at YBAL3. f Waveform comparison for line array stations. Amplitudes normalized by maximum pressure at synthetic YIB21

We ran five separate simulations with lower boundaries corresponding to the topographic profiles along azimuths between the south vent and each receiver in the rim network (YIF1–YIF5; Fig. 2). We modeled a single event when the aerostat was located near YIF3 (August 1, 2016, at 04:53:12.87 UTC). Since the method is a forward model, the source pressure must be adjusted to approximate the amplitudes observed at the receivers. We chose a maximum source pressure of 7000 Pa to approximate the peak pressure at YBAL3 (Fig. 5e). We used a homogeneous atmospheric sound speed of 346 m/s, which corresponds to observed temperatures during the deployment (Iezzi et al. 2019) and gives reasonable arrival times across the network (Fig. 5e). We used a 4 × 4 km model space and 10 s simulation run time such that the wavefront does not reach (or spuriously reflect from) the top or right boundaries.

Finite-difference models require adequate discretization in time and space to ensure numerical accuracy at the frequencies of interest. Taflove and Hagness (2005) stated that at least 10 grid nodes per wavelength are required. For a grid spacing ∆ and maximum sound speed c_max, the corresponding time step ∆t must also meet the Courant–Friedrichs–Lewy condition $\Delta \mathrm{t }\le \Delta {c}_{max}\sqrt{3}$ (Taflove and Hagness 2005). In our method, the discretization and frequency content is determined as a function of the number of nodes per wavelength desired at a maximum source frequency and minimum sound speed in the model. For example, an input of 10 nodes per wavelength at 5 Hz and 340 m/s yields ∆ = 5.9 m, ∆t = 4.7 ms, and 30–50 nodes per wavelength at dominant frequencies around 1 Hz (de Groot-Hedlin 2017). In this study, we chose 25 nodes per wavelength at 6 Hz and 346 m/s, yielding ∆ = 2.3 m and ∆t = 1.9 ms. This gives 75–125 nodes per wavelength at dominant frequencies around 1.5 Hz and 19–50 nodes per wavelength in our primary analysis band of 3–8 Hz. The Courant–Friedrichs–Lewy condition for numerical accuracy at 10 nodes per wavelength is met up to 15 Hz; above this frequency, artifacts from numerical dispersion may become significant. Note that Maher et al. (2020) performed a finely discretized simulation with 40 nodes per wavelength to check for inaccuracies due to numerical dispersion, but they did not observe changes to the frequency components of interest in their study. We are therefore confident in the numerical accuracy of our simulations at the frequencies of interest for ν_N analysis at Yasur Volcano (∼3–8 Hz).

Modeling results

We ran five simulations, one for each topographic profile from the south vent to each receiver in the crater rim network and recorded synthetic waveforms at 14 locations corresponding to the active sensors during an event on August 1, 2016, at 04:53:12.87 UTC. The three aerostat sensors were located near YIF3 and so were included in the YIF3 simulation with positions shown in Fig. 5b. The line array sensor positions coincide with the YIF4 profile and so were included in the YIF4 simulation as shown in Fig. 5d. Figures 5a–d shows example snapshots of the wavefield at different times in four of the simulations (YIF2 not shown). The maximum pressures are concentrated at the wavefront, though reflection from the crater walls and rim creates complexity in the trailing wavefield. Figure 5e shows that the synthetic waveforms (black lines) show good agreement in relative amplitudes and arrival times with the observations (colored lines). In some cases, the observed waveforms feature more rapid compressional onsets than the synthetics (e.g., YBAL3 and YIF3). This feature is likely a result of the spatially distributed Gaussian source function (see “Finite-difference method” section).

The PSD and ν_N spectra corresponding to the waveforms in Fig. 5e are shown in Fig. 6. Results are grouped in columns by sensor locations; i.e., results for aerostat sensors, crater rim stations, and line array elements are shown in the first, second, and third columns, respectively. The first row (Fig. 6a–c) shows PSD for synthetics (grayscale) and observations (color), the second row (Fig. 6d–f) shows ν_N spectra for the synthetics, and the third row (Fig. 6g–i) shows ν_N for the observations. Synthetic and observed power spectra generally agree in peak power and dominant frequencies (∼1–3 Hz), although the synthetic spectra roll off rapidly toward the upper limit of numerical accuracy at 15 Hz (“Finite-difference method” section). The ν_N spectra feature the expected reclined S-shape for both synthetics and observations, indicating energy transfer from ∼4–5 to 6–7 Hz. The ν_N magnitudes are larger for the synthetics than the observations (e.g., 10⁻³ dB/m at the synthetic line array vs 10⁻⁴ dB/m in the observations), and the minima in synthetic ν_N occur at frequencies approximately 0.5 Hz higher than in the observed ν_N.

Fig. 6

Spectra corresponding to the waveforms shown in Fig. 5e. a–c PSD curves for synthetic waveforms (grayscale) and corresponding observed waveforms (color) for an event at 04:53:12.87 on August 1, 2016. Spectra are grouped by sensors at the aerostat (first column), crater rim (second column), and line array (third column). d–f ν_N curves for synthetic signals at the aerostat, crater rim, and line array sensors, respectively. g–i) ν_N curves for observed signals at the aerostat, crater rim, and line array sensors, respectively. Note the smaller scale on the y-axis in g–i than d–f

Cumulative distortion and source volume estimation

Here we present a technique for using observed ν_N to estimate the error in source volume calculations due to nonlinear propagation effects. The principle is to estimate cumulative nonlinear distortion (ν_Ntot) and use it as a correction factor for a source spectrum obtained assuming linear propagation. The source volume estimates can then be compared using the linear and nonlinear-corrected source spectra as inputs.

Cumulative nonlinear distortion

The first step is to use observed ${\nu }_{N}$ measurements to estimate cumulative nonlinear changes (ν_Ntot) between the source and each station. Since the goal is to directly subtract ν_Ntot power spectra, ν_N must first be converted to a suitable unit. The decibel unit of ${\nu }_{N}$ is not the same as the unit used for sound-pressure levels representing power spectral density. Sound-pressure levels (L_p) are represented by Eq. 2, whereas ${\nu }_{N}$ represents a change in L_p with distance (Miller 2016) in unit dB/m:

$${\nu }_{N} = \underset{\mathit{dx}\to 0}{\mathrm{lim}}\frac{10{\mathrm{log}}_{10}\left({p}_{2}^{2}/{p}_{\mathrm{ref}}^{2}\right)-10{\mathrm{log}}_{10}\left({p}_{1}^{2}/{p}_{\mathrm{ref}}^{2}\right)}{dx} = \underset{\mathit{dx}\to 0}{\mathrm{lim}}\frac{10{\mathrm{log}}_{10}\left({p}_{2}^{2}/{p}_{1}^{2}\right)}{dx},$$

(4)

where p₁ is pressure measured at distance x and p₂ is hypothetical pressure at a small distance away (x + dx). Solving for the derivative of squared pressure gives ${\nu }_{N}$ in the desired unit of Pa²/m (Miller 2016):

$$\frac{d{p}^{2}}{dx}=\underset{\mathit{dx}\to 0}{\mathrm{lim}}\frac{{p}_{2}^{2}-{p}_{1}^{2}}{dx}=\underset{\mathit{dx}\to 0}{\mathrm{lim}}\frac{{p}_{1}^{2}}{dx}\left({10}^{{\nu }_{N}dx/10-1}\right)=\frac{{p}_{1}^{2}{\nu }_{N}}{10}ln\left(10\right).$$

(5)

The converted ${\nu }_{N}$ values have units of Pa²/m, so integration of each frequency component over the source-receiver distance will give a cumulative distortion estimate (ν_Ntot) in unit Pa². Since the evolution of ν_N between the source and most proximal receiver is not known, an assumption must be made as to the spatial rate of change. Maher et al. (2020) assumed a constant rate such that ${\nu }_{N\mathrm{tot}}={\nu }_{N}\times r$, but this is unlikely to be true because nonlinear propagation effects should increase with amplitude toward the source. Here we assume that the rate increases toward the source by 1/r, in proportion with pressure amplitudes for spherical spreading.

The ${\nu }_{N\mathrm{tot}}$ calculation process is illustrated in Fig. 8. Observed ${\nu }_{N}$ spectra (unit dB/m) are shown in Fig. 8a for a single event at stations along a single azimuth from the crater (YIF4 and YIB11–YIB23). In Fig. 8b, the ${\nu }_{N}$ spectra are converted to unit Pa²/m with Eq. 5. In Fig. 8c, ${\nu }_{N}$ values are extracted at six frequency components and plotted as a function of source-receiver distance. Curves for 1/r decay are fit to the values at the closest station (YIF4). The observed ${\nu }_{N}$ values at the line array are less than predicted by 1/r decay for lower frequencies (3, 4, and 5 Hz), however, the observed values are likely lower than true due to topographic effects, as illustrated by numerical modeling in Fig. 7f. Integration of the 1/r curves for every frequency component from r = 1 m to each station yields the cumulative distortion spectra (${\nu }_{N\mathrm{tot}}$) in Fig. 8d. These curves largely overlap since most of the distortion occurs in the near-source region.

Fig. 7

Comparison of synthetic spectra for simulations with topography (color) versus flat ground (grayscale). a–c PSD for aerostat, crater rim, and line array sensors, from left to right respectively. d–e ν_N for aerostat, crater rim, and line array sensors, from left to right, respectively

Fig. 8

a ν_N for the observed event at 04:53:12 on August 1, 2016. b The same ν_N converted to units of Pa²/m. c ν_N values as a function of distance for six frequency components. Colored lines show 1/r fit to ν_N values at YIF4. d Cumulative ν_N (ν_Ntot; unit Pa²) at each station. e Observed power spectral densities for the event. f Source power spectra (S_pp divided by the PSD of synthetic Green’s function, S_gg). g Source volume estimates based on linear source spectra (blue squares) and ν_Ntot–corrected source spectra (yellow diamonds). h Percentage difference in source volume estimate between linear and nonlinear source spectra

Volume estimation

The second step is to estimate source volumes (V) from power spectra using ${\nu }_{N\mathrm{tot}}$ (Fig. 8d) as a correction term for nonlinearity. Our motivation is to approximate the errors associated with the nonlinear propagation effect rather than to robustly determine source volume, which requires accounting for source directionality, atmospheric conditions, and other factors (Iezzi et al. 2019). Consequently, we use a relatively simple single-station approach to volume estimation, which assumes a monopole source and the equivalence of excess pressure to the rate of change of displaced atmosphere at the source (Lighthill 1978). The method is based on this classic monopole assumption (e.g., Vergniolle et al. 2004; Moran et al. 2008; Johnson and Miller 2014; Yamada et al. 2017):

$$V = \frac{2\pi r}{{\rho }_{0}}{\iint }_{{t}_{1}}^{{t}_{2}}[p(r,t)]{dt}^{2},$$

(6)

where t₁ and t₂ are the starting and ending times of the signal. We modify Eq. 6 to operate in the frequency domain assuming Parseval’s theorem, and we further correct the power spectra to account for topographic effects by dividing by the PSD of a synthetic Green’s function:

$$V = \frac{1}{{\rho }_{0}}{\iint }_{\sqrt{{f}_{1}}}^{\sqrt{{f}_{2}}}\left[\frac{\sqrt{{S}_{pp}}}{\sqrt{{S}_{gg}}}\right]d\sqrt{f},$$

(7)

where ${S}_{pp}$ are ${S}_{gg}$ power spectral densities of the signal and the Green’s function, respectively. Note that square roots are taken to ensure units of Pa, and the spherical spreading term in Eq. 6 ($2\pi r)$ is implicit in the Green’s function. We use Green’s functions generated by linear three-dimensional (3D) finite-difference simulations as described and parametrized by Iezzi et al. (2019), which account for topography (2-m grid spacing) and a homogenous sound speed of 346.4 m/s. We normalize the Green’s functions by the peak amplitude of the source function (1 Pa).

Equation 7 represents the volume based on linear propagation; accounting for nonlinearity takes the form:

$$V = \frac{1}{{\rho }_{0}}{\iint }_{\sqrt{{f}_{1}}}^{\sqrt{{f}_{2}}}\frac{\sqrt{{S}_{pp}}}{\sqrt{{S}_{gg}}}-{\nu }_{N\mathrm{tot}}d\sqrt{f}.$$

(8)

Subtraction of ${\nu }_{N\mathrm{tot}}$ means that that power lost to nonlinearity during propagation (negative ${\nu }_{N}$) is reintroduced to the source spectra and vice versa.

The volume estimation process is illustrated in Fig. 8. Observed power spectra are shown in Fig. 8e for a single event at stations along a single azimuth from the crater (YIF4 and YIB11–YIB23). In Fig. 8f, the power spectra are divided by the Green's functions to give the estimated source spectra for linear propagation. Source volume estimates for linear (Eq. 7) and nonlinear propagation (Eq. 8) are shown in Fig. 8 g. The volume estimates are reasonable (10⁴ m³) in comparison to previous results from full-waveform inversion (Iezzi et al. 2019). The percentage difference between linearly and nonlinearly estimated source volumes ($\Delta V$) are very small (10⁻⁸%) (Fig. 8h). Although the percentage difference is negligible, the negative values indicate that volumes are underestimated rather than overestimated using the linear assumption, in agreement with previous work (Watson et al. 2021). We expect larger differences for signals that are higher amplitude (more nonlinear) than considered here, such as for Vulcanian or Plinian eruptions.

In Fig. 9, we investigate variations in ${\nu }_{N}$, $V$, and $\Delta V$ with peak waveform amplitude (p_max) at one station (YIF4) for 2068 events on July 31st and August 1st, when explosivity increased and shifted predominantly to the south vent (Jolly et al. 2017; Iezzi et al. 2019; Fitzgerald et al. 2020; Matoza et al. 2022). We detect these events with a simple peak-finder algorithm (Duarte and Watanabe 2018; Matoza et al. 2022) using a minimum event separation time of 60 s and amplitude threshold of 1 Pa. As expected, the ${\nu }_{N}$ magnitudes (Fig. 9d) and linear volume estimates (Fig. 9e) increase with p_max. The relationships appear to be linear over the entire amplitude range (3–665 Pa), suggesting that there is not a threshold amplitude value below which nonlinear propagation effects are insignificant. The magnitudes (absolute values) of $\Delta V$ values also increase with p_max as expected (Fig. 9f), but the values are very small (< 10⁻⁷%). There are both positive and negative trends in Fig. 9f, but only the negative trend is expected since linearly estimated volumes are expected to be smaller than true (Maher et al. 2019; Watson et al. 2021). We interpret these results to suggest that nonlinear propagation effects are present, but they are either not accurately quantified by ${\nu }_{N}$ or they do not cause a significant error (i.e., > 1%) in source volume estimates.

Fig. 9

a Waveform at YIF4 on July 31 and August 1, 2016. b Peak amplitudes (p_max) of each picked event. c Maximum ν_N values between 3 and 8 Hz for each picked event. d Comparison of maximum ν_N with peak amplitudes. e Comparison of linear source volume estimates with peak amplitudes. f Percentage difference between linear and nonlinear source volume estimates as a function of peak amplitude

Discussion

We applied a single-point quadspectral density nonlinearity indicator (ν_N) to waveforms primarily from 80 explosion events at Yasur Volcano recorded by 14 sensors located between ∼200 and 1080 m from the source and to synthetic waveforms generated by nonlinear wavefield modeling for one event. In both the synthetic ν_N and many observational results, we observe a qualitative resemblance to the reclined S-shape previously observed for supersonic model-scale jet noise (Fig. 1; Miller and Gee 2018). The feature generally occurs below 10 Hz and suggests spectral energy transfer from lower frequencies (5–6 Hz) to higher frequencies (6–10 Hz), while results at frequencies greater than ∼10 Hz are made uncertain by high variance and low signal-to-noise ratio. The ν_N magnitudes decrease with distance as expected from theory (Reichman et al. 2016a) and previous observations for frequencies of 600–40,000 Hz (Miller and Gee 2018).

Comparison of observations to previous studies

The ν_N indicator is a relatively new method that has been applied to only a few datasets, making our results a novel contribution but also complicating their interpretation. Reichman et al. (2016a) derived the expression from the spectral generalized Burgers equation presented by Morfey and Howell (1981). They demonstrated the predicted behavior of ν_N through application to two numerical solutions to the generalized Burgers equation for an initially sinusoidal plane wave. They observed expected changes with distance in the spectral level of harmonics on the sinusoid frequency, showing that ν_N quantifies spectral energy transfer in an idealized case. Miller and Gee (2018) applied ν_N to jet noise signals (600–40,000 Hz) recorded over a range in distances and angles from a supersonic model-scale jet in an anechoic chamber. They found good agreement between observed ν_N and theory, with a reclined S-shape and magnitudes decreasing with range (Fig. 1c). Finally, Maher et al. (2020) were the first to apply ν_N to infrasonic frequencies, using data and synthetics corresponding to signals from eruptions at Sakurajima Volcano in Japan (0.1–10 Hz). Their results from the synthetic signals exhibited reclined S-shaped indicative of upward spectral energy transfer. However, they found inconclusive ν_N results from the observed waveforms and speculated on complications related to outdoor propagation (e.g., wind, topography, ground impedance) and source dynamics (e.g., fluid flow and jet turbulence).

We find good agreement in ν_N magnitudes between the Yasur Volcano observations and results from supersonic model scale jet noise at audible frequencies (Miller and Gee, 2018) and Sakurajima Volcano eruptions at infrasonic frequencies (Maher et al., 2020). For large-amplitude signals from the Yasur Volcano’s south vent at YIF4, we observe ν_N on the order of 10⁻³ dB/m at a distance of 261 m (Fig. 9d). Assuming an approximately 10 m vent diameter (D_j), our result corresponds to 10⁻² dB/D_j at 26 D_j, which is comparable to ν_N magnitudes observed by Miller and Gee (2018) at 20–30 D_j for frequencies ∼1–40 kHz (Fig. 1c). Maher et al. (2020) integrated Sakurajima Volcano ν_N results with respect to distance, assuming a constant rate of change to obtain a cumulative estimate of total nonlinear changes (ν_Ntot). They found consistent ν_Ntot magnitudes of ≤ 2 dB in observational results and synthetics with a wide range of topography and wind conditions. For ν_N = 10⁻³ dB/m at YIF4 and 261 m to the south vent, ν_Ntot = 0.261 dB. Although this value is smaller than obtained at Sakurajima Volcano, the waveform amplitudes at Yasur Volcano are also lower than at Sakurajima Volcano, so the nonlinear processes are expected to be weaker.

Marchetti et al. (2013) observed wavefront speeds of 341–403 m/s in thermal imagery and estimated Mach numbers (Ma = u/c₀, where u is wave velocity) of up to 1.28 using the Rankine–Hugoniot relation for fluid properties across a one-dimensional shock wave (Dewey 2018):

$${p}_{0}={p}_{\text{atm}}\left[1+\frac{2\upgamma }{\upgamma +1}\left(M{a}^{2}-1\right)\right],$$

(9)

where ${p}_{\text{atm}}$ is the atmospheric pressure (10⁵ Pa), $\gamma =1.4$ is heat capacity of dry air, ${p}_{0}$ = ${p}_{\text{atm}}$ + ${p}_{\text{acu}}$ $\times r$, and ${p}_{\text{acu}}$ is the observed acoustic pressure. The waveforms recorded in our experiment are higher in amplitude than those analyzed by Marchetti et al. (2013); they observed peak amplitudes of up to 106 Pa at 700 m, whereas we observe up to 665 Pa at 261 m (~ 248 Pa when scaled to 700 m) (e.g., Fig. 9). According to Eq. 9, this amplitude corresponds to Mach 1.58, or a propagation speed at the source of 546 m/s assuming an ambient velocity of 346 m/s.

Marchetti et al. (2013) also showed a comparison of amplitude-normalized waveform properties to the Friedlander equation (Reed 1977) for blast waves from chemical explosions. While the general shape of the Friedlander equation is reminiscent of Yasur explosion waveforms, appropriate scaling of the Friedlander equation for distance and amplitude is known to provide poor fits to observed waveforms (Garces 2019). Matoza et al. (2019) showed that accurate scaling of the Friedlander equation results in over-prediction of source strength for a waveform at Sakurajima Volcano. The Friedlander equation was empirically derived for blast waves from the detonation of chemical high explosives, whereas volcano acoustic source processes are slower and more closely resemble boiling liquid expanding vapor explosions (Garcés et al. 2013). In contrast, the ν_N indicator is based on the generalized Burgers equation, which is an analytical description of finite-amplitude wave steepening that makes no assumption of the sourcing process. The generalized Burgers equation is valid for weakly nonlinearity ($\left|p\right|\ll {\rho }_{0}{c}_{0}^{2}$) (Reichman et al. 2016a), or overpressures less than 141,265 Pa for ${\rho }_{0}$ = 1.18 kg/m³ and ${c}_{0}$ = 346 m/s.

Difference between observations and synthetics

We modeled waveforms, PSDs, and ν_N spectra for a single event Yasur Volcano using a finite-difference method for nonlinear infrasound propagation (de Groot-Hedlin 2017) and found good agreement in waveform arrival times and amplitudes (Fig. 5e), spectral power at dominant frequencies of 1 to 3 Hz (Fig. 6a–c), and ν_N spectral shape in the band 3–8 Hz (Fig. 6d–i). However, the magnitudes of ν_N are larger for the synthetics than the observations. This difference suggests stronger nonlinearity in the simulations than in the observed event, which may be related to the limitations of the modeling method. Although near-source topography may significantly modulate the acoustic wavefield (e.g., Kim and Lees 2011; Matoza et al., 2009), our modeling method requires that topography must be flat in the source region to maintain numerical stability (“Finite-difference method” section). This required us to add artificial 175 m-wide flat surfaces into the crater area of the topographic profiles for each simulation (see Figs. 5a–d), causing the receivers to fall further from the center of the source. We consequently used a higher maximum source pressure than expected in order to overcome the extra amplitude losses from geometrical spreading. Since the method uses a forward approach, we adjusted the source pressure to approximate the peak amplitude at the closest receiver (YBAL3). This same interpretation explains why the minima in synthetic ν_N occur at frequencies ∼0.5 Hz higher than in the observations (e.g., 5.5 Hz in Fig. 6e vs 5 Hz in Fig. 6h); stronger nonlinearity results in distortions at higher frequencies. Increased spectral energy transfer to higher frequencies at larger source pressures has been previously observed in nonlinear infrasound modeling (de Groot-Hedlin 2012, 2016, 2017; Maher et al. 2020).

We additionally tested for the effect of topography on synthetic ν_N by generating a simulation with the source and receivers on the ground at sea level. In this case, horizontal source distances were the same as in the topography simulations, and the aerostat receivers were the same height above the surface. The source pressure was kept the same to isolate the effect of topography. Figure 7 compares the synthetic PSD (Fig. 7a–c) and ν_N results (Fig. 7d–f) for the topography simulations (color) and flat ground (grayscale). The spectral shapes and magnitudes are comparable between the simulations for the crater rim (Fig. 7b,e) and line array sensors (Fig. 7c,f), suggesting minimal complications from topography. In contrast, at the aerostat sensors, the magnitudes of PSD (Fig. 7a) and ν_N (Fig. 7d) are lower for the flat ground simulation than the topography simulation. This result may reflect the influence of acoustic focusing: in the topography case, multiple reflections up the crater wall constructively interfere to increase pressure at the aerostat. In the case of a flat lower boundary, the ground reflection does not constructively interfere with the wavefront at the aerostat location, resulting in lower amplitudes.

Finally, we note 3D wavefield interactions with topography outside the source-receiver plane may introduce differences between synthetics and observations. The FDTD method used here operates in a 2D source-receiver plane with axisymmetry about the left boundary (de Groot-Hedlin 2017), so topographic complexity outside the plane is not accounted for. Infrasound simulations at Yasur Volcano using 3D finite differences suggest that full wavefield effects may be significant (Iezzi et al. 2019; Fee et al. 2021); however, those methods assume linear propagation and do not currently allow for investigation of nonlinear propagation effects. Maher et al. (2021) compared the effects of topography on simulated waveforms for Sakurajima Volcano using a linear version of the FDTD method used here (de Groot-Hedlin 2016) and the 3D Cartesian FDTD method developed by Kim and Lees (2014) and later used by Iezzi et al. (2019) and Fee et al. (2021). Maher et al. (2021) found that synthetic amplitudes were more strongly reduced by topographic effects (diffraction, scattering) in the 2D axisymmetric method than in the 3D Cartesian method, but both methods yielded similar relative amplitude distributions across an azimuthally distributed network with varying topography. From this, we conclude that the simulations with Yasur Volcano topography may feature stronger topographic attenuation than true; however, we also ran simulations with flat ground that produced similar ν_N results at the crater rim and line array stations (Fig. 7e,f). A FDTD method that incorporates both 3D topography and nonlinear propagation is desirable but outside the scope of the present work.

Limitations of the ν _N method

Although our ν_N results show strong evidence for nonlinear propagation in higher-amplitude Yasur Volcano signals, several challenges remain in using the method as a quantitative indicator.

Firstly, our assessment of a clear result is made on the basis of qualitative comparison to previous results from supersonic jet noise that is known to propagate nonlinearly (Fig. 1; Miller and Gee 2018). A more quantitative assessment of result quality is desired, but the construction of such a method is outside the scope of this study.

Secondly, we observe clear ν_N signatures in the band 3–9 Hz (e.g., Fig. 4) but find high variance results at higher frequencies that do not accurately quantify nonlinear energy transfer (∼10 Hz to Fs/4; Fig. 3g–i). In this study, we introduced a spectral signal-to-noise threshold that screens ν_N at some higher frequencies (e.g., > 40 Hz in Fig. 3i) but does not completely eliminate the ν_N results that are presumed spurious. Further work is needed to adapt ν_N to infrasound and determine appropriate frequency bounds in the presence of outdoor noise sources, which were not an issue for previous studies by Reichman et al. (2016a) and Miller and Gee (2018).

Finally, we note that the use of power spectral density is not ideal for discrete explosions since the assumption of signal stationarity in the Fourier transform is not met. For Yasur Volcano, the explosion signals are only a few seconds in duration, but PSD estimation requires longer time windows (10¹ s) to ensure accuracy at low frequencies. Several seconds of ambient noise must therefore be included in the windows, leading to underestimation of spectral power when values are averaged across signal and noise. Additionally, the asymmetric nature of the waveforms results in non-zero signal means, which translates to spectral leakage and spurious non-zero power at low frequencies. Despite these limitations, PSD estimates are commonly used in volcano infrasound studies, and it is required for the ν_N method as currently formulated (Eq. 3). Future work should consider the use of energy spectral density (e.g., Haskell 1964; Kanamori and Anderson 1975; Garces 2013) or wavelet transforms (e.g., Lees and Ruiz 2008; Cannata et al. 2013; Lapins et al. 2020), which are better suited to impulsive and nonstationary signals.

Conclusions

We investigated infrasound signals from Strombolian explosion events at Yasur Volcano using a single-point frequency-domain indicator of nonlinear propagation (ν_N; Reichman et al. 2016a). We hypothesized that the ν_N method would quantify spectral energy transfer associated with nonlinear wavefield changes at infrasonic frequencies (0.1–20 Hz) similar to what was previously observed in experiments with supersonic model-scale jet noise at audible frequencies (600–40,000 Hz) (Miller and Gee 2018). Our ν_N results for the larger amplitude events (∼102 Pa at 200–300 m) resemble those of the jet noise study both in relative spectral character (the reclined S-shape around 3–9 Hz) and in magnitude (10⁻² dB/D_j at 20–30 D_j). The clarity of the ν_N signature increases with peak waveform amplitude, consistent with expectations of stronger nonlinearity at higher pressures. We interpret these results as evidence for nonlinear acoustic propagation whereby wave steepening causes spectral energy transfer from frequency components at 3–6 Hz to higher frequencies (6–8 Hz).

We further performed finite-difference simulations of nonlinear infrasound propagation (de Groot-Hedlin 2017) to model waveforms, power spectra, and ν_N results for a representative Yasur Volcano event. Despite limitations in the model, we observe similar ν_N spectral shapes in synthetics in the band 3–8 Hz, corroborating the nonlinearity quantified in the observations. Challenges remain in accurately accounting for both topography and nonlinearity in finite-difference simulations.

Our results confirm previous interpretations of nonlinear propagation at Yasur Volcano on the basis of asymmetric waveforms (Marchetti et al. 2013). We also extend the work of Maher et al. (2020), who observed clear ν_N signatures for synthetics but not observations at Sakurajima Volcano by showing these ν_N spectral shapes for both observations and synthetics at Yasur Volcano. This suggests that infrasound-based source parameter estimates based on linear propagation at Yasur Volcano and other volcanoes may give inaccurate results, e.g., underestimation of erupted volume (Maher et al. 2019; Watson et al. 2021). We made preliminary calculations of < 1% error in source volume estimates using a simple single-station monopole approach, which suggests that source parameter estimates for these data are not greatly affected by nonlinear propagation effects. However, larger errors are expected for more explosive eruption styles at other volcanoes (e.g., Vulcanian and Plinian eruptions), and future work is needed to fully account for nonlinear processes in source parameter estimation.