Skip to main content
SpringerLink
Log in

Limits of the boundary of random planar maps

  • Published:
Probability Theory and Related Fields Aims and scope Submit manuscript

Abstract

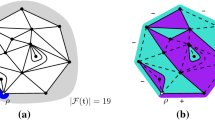
We discuss asymptotics for the boundary of critical Boltzmann planar maps under the assumption that the distribution of the degree of a typical face is in the domain of attraction of a stable distribution with parameter \(\alpha \in (1,2)\). First, in the dense phase corresponding to \(\alpha \in (1,3/2)\), we prove that the scaling limit of the boundary is the random stable looptree with parameter \(1/(\alpha -1/2)\). Second, we show the existence of a phase transition through local limits of the boundary: in the dense phase, the boundary is tree-like, while in the dilute phase corresponding to \(\alpha \in (3/2,2)\), it has a component homeomorphic to the half-plane. As an application, we identify the limits of loops conditioned to be large in the rigid \(O(n)\) loop model on quadrangulations, proving thereby a conjecture of Curien and Kortchemski.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Abraham, R., Delmas, J.-F.: Local limits of conditioned Galton–Watson trees: the condensation case. Electron. J. Probab. 19(56), 1–29 (2014)

    MathSciNet  MATH  Google Scholar 

  2. Abraham, R., Delmas, J.-F.: Local limits of conditioned Galton–Watson trees: the infinite spine case. Electron. J. Probab. 19, 1–19 (2014)

    MathSciNet  MATH  Google Scholar 

  3. Aldous, D.: The continuum random tree. I. Ann. Probab. 19(1), 1–28 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  4. Aldous, D.: The continuum random tree III. Ann. Probab. 21(1), 248–289 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  5. Ambjørn, J., Budd, T., Makeenko, Y.: Generalized multicritical one-matrix models. Nucl. Phys. B 913(Supplement C), 357–380 (2016)

    Article  MATH  Google Scholar 

  6. Baur, E., Richier, L.: Uniform infinite half-planar quadrangulations with skewness. arXiv:1612.08572 [math] (2016)

  7. Berestycki, N., Laslier, B., Ray, G.: Critical exponents on Fortuin Kasteleyn weighted planar maps. Commun. Math. Phys. 355(2), 427–462 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bernardi, O., Curien, N., Miermont, G.: A Boltzmann approach to percolation on random triangulations. arXiv:1705.04064 [math] (2017)

  9. Bertoin, J., Budd, T., Curien, N., Kortchemski, I.: Martingales in self-similar growth-fragmentations and their connections with random planar maps. arXiv:1605.00581 [math-ph] (2016)

  10. Bingham, N.H., Goldie, C.M., Teugels, J.L.: Regular Variation. Cambridge University Press, Cambridge (1989)

    MATH  Google Scholar 

  11. Björnberg, J.E., Stefánsson, S.O.: Random walk on random infinite Looptrees. J. Stat. Phys. 158(6), 1234–1261 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  12. Borot, G., Bouttier, J., Guitter, E.: Loop models on random maps via nested loops: case of domain symmetry breaking and application to the Potts model. J. Phys. A Math. Theor. 45(49), 494017 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. Borot, G., Bouttier, J., Guitter, E.: More on the O(n) model on random maps via nested loops: loops with bending energy. J. Phys. A Math. Theor. 45(27), 275206 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Borot, G., Bouttier, J., Guitter, E.: A recursive approach to the O(n) model on random maps via nested loops. J. Phys. A Math. Theor. 45(4), 045002 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Bouttier, J., Di Francesco, P., Guitter, E.: Planar maps as labeled mobiles. Electron. J. Combin. 11(1), R69 (2004)

    MathSciNet  MATH  Google Scholar 

  16. Bouttier, J., Guitter, E.: Distance statistics in quadrangulations with a boundary, or with a self-avoiding loop. J. Phys. A Math. Theor. 42(46), 465208 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  17. Brézin, E., Itzykson, C., Parisi, G., Zuber, J.-B.: Planar diagrams. Commun. Math. Phys. 59(1), 35–51 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  18. Budd, T.: The peeling process of infinite Boltzmann planar maps. Electron. J. Combin. 23(1), 1–28 (2016)

    MathSciNet  MATH  Google Scholar 

  19. Budd, T., Curien, N.: Geometry of infinite planar maps with high degrees. Electron. J. Probab. 22(35), 1–37 (2017)

  20. Budd, T.: With an appendix jointly with L. Chen. The peeling process on random planar maps coupled to an O(n) loop model (2017) (in preparation)

  21. Burago, D., Burago, Y., Ivanov, S.: A Course in Metric Geometry. Graduate Studies in Mathematics. American Mathematical Society, Providence (2001)

    MATH  Google Scholar 

  22. Chen, L.: Basic properties of the infinite critical-FK random map. Ann. Inst. Henri Poincaré Comb. Phys. Interact 4(3), 245–271 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  23. Chen, L., Curien, N., Maillard, P.: The perimeter cascade in critical Boltzmann quadrangulations decorated by an O(n) loop model. arXiv:1702.06916 [math-ph] (2017)

  24. Curien, N.: Peeling Random Planar Maps. Cours Peccot, Collège de France, Paris (2016)

    Google Scholar 

  25. Curien, N., Haas, B., Kortchemski, I.: The CRT is the scaling limit of random dissections. Random Struct. Alg. 47(2), 304–327 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  26. Curien, N., Kortchemski, I.: Percolation on random triangulations and stable looptrees. Probab. Theory Relat. Fields 163(1–2), 303–337 (2014)

    MathSciNet  MATH  Google Scholar 

  27. Curien, N., Kortchemski, I.: Random stable looptrees. Electron. J. Probab. 19(108), 1–35 (2014)

    MathSciNet  MATH  Google Scholar 

  28. Curien, N., Miermont, G.: Uniform infinite planar quadrangulations with a boundary. Random Struct. Alg. 47(1), 30–58 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  29. Duquesne, T.: A limit theorem for the contour process of conditioned Galton–Watson trees. Ann. Probab. 31(2), 996–1027 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  30. Duquesne, T., Le Gall, J.-F.: Random Trees, Lévy Processes and Spatial Branching Processes. Société Mathématique de France, Marseille (2002)

    MATH  Google Scholar 

  31. Duquesne, T., Le Gall, J.-F.: Probabilistic and fractal aspects of Lévy trees. Probab. Theory Relat. Fields 131(4), 553–603 (2005)

    Article  MATH  Google Scholar 

  32. Flajolet, P., Sedgewick, R.: Analytic Combinatorics. Cambridge University Press, Cambridge (2009)

    Book  MATH  Google Scholar 

  33. Gwynne, E., Mao, C., Sun, X.: Scaling limits for the critical Fortuin–Kasteleyn model on a random planar map I: cone times. arXiv:1502.00546 [math-ph] (2015)

  34. Gwynne, E., Sun, X.: Scaling limits for the critical Fortuin–Kastelyn model on a random planar map III: finite volume case. arXiv:1510.06346 [math-ph] (2015)

  35. Gwynne, E., Sun, X.: Scaling limits for the critical Fortuin–Kasteleyn model on a random planar map II: local estimates and empty reduced word exponent. Electron. J. Probab. 22(45), 1–56 (2017)

  36. Janson, S.: Simply generated trees, conditioned Galton–Watson trees, random allocations and condensation. Probab. Surv. 9, 103–252 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  37. Janson, S., Stefánsson, S.O.: Scaling limits of random planar maps with a unique large face. Ann. Probab. 43(3), 1045–1081 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  38. Jonsson, T., Stefánsson, S.O.: Condensation in nongeneric trees. J. Stat. Phys. 142(2), 277–313 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  39. Kesten, H.: Subdiffusive behavior of random walk on a random cluster. Ann. Inst. Henri Poincaré Probab. Stat. 22(4), 425–487 (1986)

    MathSciNet  MATH  Google Scholar 

  40. Kortchemski, I.: A simple proof of Duquesne’s theorem on contour processes of conditioned Galton–Watson trees. In: Donati-Martin, C., Lejay, A., Rouault, A. (eds.) Séminaire de Probabilités XLV. Lecture Notes in Mathematics, vol. 2078, pp. 537–558. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-319-00321-4

    MATH  Google Scholar 

  41. Kortchemski, I.: Limit theorems for conditioned non-generic Galton–Watson trees. Ann. Inst. Henri Poincaré Probab. Stat. 51(2), 489–511 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  42. Le Gall, J.-F.: Random trees and applications. Probab. Surv. 2, 245–311 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  43. Le Gall, J.-F.: The topological structure of scaling limits of large planar maps. Invent. Math. 169(3), 621–670 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  44. Le Gall, J.-F.: Geodesics in large planar maps and in the Brownian map. Acta Math. 205(2), 287–360 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  45. Le Gall, J.-F.: Uniqueness and universality of the Brownian map. Ann. Probab. 41(4), 2880–2960 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  46. Le Gall, J.-F., Miermont, G.: Scaling limits of random planar maps with large faces. Ann. Probab. 39(1), 1–69 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  47. Le Gall, J.-F., Paulin, F.: Scaling limits of bipartite planar maps are homeomorphic to the 2-sphere. GAFA Geom. Funct. Anal. 18(3), 893–918 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  48. Lyons, R., Peres, Y.: Probability on Trees and Networks. Cambridge University Press, Cambridge (2016)

    Book  MATH  Google Scholar 

  49. Marckert, J.-F., Miermont, G.: Invariance principles for random bipartite planar maps. Ann. Probab. 35(5), 1642–1705 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  50. Marckert, J.-F., Mokkadem, A.: Limit of normalized quadrangulations: the Brownian map. Ann. Probab. 34(6), 2144–2202 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  51. Marzouk, C.: Scaling limits of random bipartite planar maps with a prescribed degree sequence. arXiv:1612.08618 [math] (2016)

  52. Miermont, G.: An invariance principle for random planar maps. In: Fourth Colloquium on Mathematics and Computer Science. DMTCS Proceedings, vol. AG, pp. 39–58 (2006)

  53. Miermont, G.: The Brownian map is the scaling limit of uniform random plane quadrangulations. Acta Math. 210(2), 319–401 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  54. Miermont, G., Weill, M.: Radius and profile of random planar maps with faces of arbitrary degrees. Electron. J. Probab. 13, 79–106 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  55. Neveu, J.: Arbres et processus de Galton–Watson. Ann. Inst. Henri Poincaré Probab. Stat. 22(2), 199–207 (1986)

    MathSciNet  MATH  Google Scholar 

  56. Sheffield, S.: Quantum gravity and inventory accumulation. Ann. Probab. 44(6), 3804–3848 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  57. Stephenson, R.: Local convergence of large critical multi-type Galton–Watson trees and applications to random maps. J. Theor. Probab. (2016). https://doi.org/10.1007/s10959-016-0707-3

    Article  MathSciNet  MATH  Google Scholar 

  58. Stufler, B.: Limits of random tree-like discrete structures. arXiv:1612.02580 [math] (2016)

Download references

Acknowledgements

Many thanks to Grégory Miermont for enlightening discussions and for attentively reading this work. I would also like to thank warmly Erich Baur, Jérémie Bouttier, Timothy Budd, Nicolas Curien and Igor Kortchemski for very useful discussions and comments. Finally, I am deeply indebted to the anonymous referees for their careful rereading, crucial corrections and remarks.

Author information

Authors and Affiliations

  1. CMAP, École polytechnique, Palaiseau, France

    Loïc Richier

Authors
  1. Loïc Richier
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Loïc Richier.

Additional information

This work was partially accomplished at UMPA, École Normale Supérieure de Lyon and supported by the Grant ANR-14-CE25-0014 (ANR GRAAL).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Richier, L. Limits of the boundary of random planar maps. Probab. Theory Relat. Fields 172, 789–827 (2018). https://doi.org/10.1007/s00440-017-0820-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00440-017-0820-y

Mathematics Subject Classification

Search

Navigation