Control of a laminated composite plate resting on Pasternak’s foundations using magnetostrictive layers

Abstract

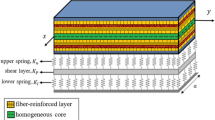
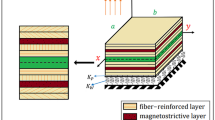
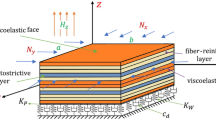
A higher-order shear deformation theory is utilized to discuss the vibration of a laminated composite plate containing four magnetostrictive layers based on Pasternak’s foundations in the current article. Hamilton’s principle is used to derive the governing dynamic equations related to the vibration of present smart structure under velocity feedback control with constant gain distributed. Navier’s approach is utilized to give a solution of simply supported laminated composite plates. Effects of all material properties, modes, thickness ratio, aspect ratio, lamination schemes, magnitude of the feedback parameter, the elastic foundations parameters and the thickness, location and number of magnetostrictive layers, on the vibration damping characteristics of the system are investigated and extensively discussed. Findings of the damping coefficients, damped natural frequencies, damping ratio, vibration time and maximum deflection for some different laminates are computed. The influences of studied parameters on the vibration suppression of plates are illustrated graphically. The results indicate increasing of smart layers structures tends to more control of structure and elastic foundations can contribute the stability of the plate significantly.

Appendices

Appendix A

The coefficients $\bar{Q}_{ij}^{\left( k \right) }$ and $\bar{q}_{ij}$ appeared in Eqs. (8) and (9) are determined as

$$\begin{aligned} \bar{Q}_{11}^{\left( k \right) }= & {} Q_{11}^{\left( k \right) }\cos ^{4}\theta ^{\left( k \right) }\mathrm {+2}\left( Q_{12}^{\left( k \right) }{\mathrm {+2}Q}_{66}^{\left( k \right) } \right) \cos ^{2}\theta ^{\left( k \right) }\sin ^{2}\theta ^{\left( k \right) } + Q_{22}^{\left( k \right) }\sin ^{4}\theta ^{\left( k \right) }, \\ \bar{Q}_{12}^{\left( k \right) }= & {} \left( Q_{11}^{\left( k \right) } + Q_{22}^{\left( k \right) }-{4Q}_{66}^{\left( k \right) } \right) \cos ^{2}\theta ^{\left( k \right) }\sin ^{2}\theta ^{\left( k \right) } + Q_{12}^{\left( k \right) }\left( \sin ^{4}\theta ^{\left( k \right) } + \cos ^{4}\theta ^{\left( k \right) } \right) , \\ \bar{Q}_{22}^{\left( k \right) }= & {} Q_{11}^{\left( k \right) }\sin ^{4}\theta ^{\left( k \right) }\mathrm {+2}\left( Q_{12}^{\left( k \right) }{\mathrm {+2}Q}_{66}^{\left( k \right) } \right) \cos ^{2}\theta ^{\left( k \right) }\sin ^{2}\theta ^{\left( k \right) } + Q_{22}^{\left( k \right) }\cos ^{4}\theta ^{\left( k \right) }, \\ \bar{Q}_{44}^{\left( k \right) }= & {} Q_{44}^{\left( k \right) }\cos ^{2}\theta ^{\left( k \right) } + Q_{55}^{\left( k \right) }\sin ^{2}\theta ^{\left( k \right) }, \\ \bar{Q}_{55}^{\left( k \right) }= & {} Q_{55}^{\left( k \right) }\cos ^{2}\theta ^{\left( k \right) } + Q_{44}^{\left( k \right) }\sin ^{2}\theta ^{\left( k \right) }, \\ \bar{Q}_{66}^{\left( k \right) }= & {} {\left( Q_{11}^{\left( k \right) } + Q_{22}^{\left( k \right) }-{2Q}_{12}^{\left( k \right) }-{2Q}_{66}^{\left( k \right) } \right) \sin ^{2}\theta ^{\left( k \right) }\cos ^{2}\theta ^{\left( k \right) } + Q}_{66}^{\left( k \right) }\left( \sin ^{4}\theta ^{\left( k \right) } + \cos ^{4}\theta ^{\left( k \right) } \right) , \\ Q_{11}^{\left( k \right) }= & {} \frac{\mathrm {1-}{\nu }_{23}^{\left( k \right) }{\nu }_{32}^{\left( k \right) }}{E_{22}^{\left( k \right) }E_{33}^{\left( k \right) }{\varDelta }}, Q_{12}^{\left( k \right) } = \frac{{\nu }_{21}^{\left( k \right) }+{\nu }_{31}^{\left( k \right) }{\nu }_{23}^{\left( k \right) }}{E_{22}^{\left( k \right) }E_{33}^{\left( k \right) }{\varDelta }} = \frac{{\nu }_{12}^{\left( k \right) }+{\nu }_{13}^{\left( k \right) }{\nu }_{32}^{\left( k \right) }}{E_{11}^{\left( k \right) }E_{33}^{\left( k \right) }{\varDelta }}, \\ Q_{22}^{\left( k \right) }= & {} \frac{\mathrm {1-}{\nu }_{13}^{\left( k \right) }{\nu }_{31}^{\left( k \right) }}{E_{11}^{\left( k \right) }E_{33}^{\left( k \right) }{\varDelta }}, G_{23}^{\left( k \right) }=Q_{44}^{\left( k \right) }, G_{13}^{\left( k \right) }=Q_{55}^{\left( k \right) }, G_{12}^{\left( k \right) }=Q_{66}^{\left( k \right) }, \\ \varDelta= & {} \frac{\mathrm {1- }{\nu }_{12}^{\left( k \right) }{\nu }_{21}^{\left( k \right) }-{\nu }_{23}^{\left( k \right) }{\nu }_{32}^{\left( k \right) }\mathrm {- }{\nu }_{13}^{\left( k \right) }{\nu }_{31}^{\left( k \right) }\mathrm {-2}{\nu }_{21}^{\left( k \right) }{\nu }_{13}^{\left( k \right) }{\nu }_{32}^{\left( k \right) }}{E_{11}^{\left( k \right) }E_{22}^{\left( k \right) }E_{33}^{\left( k \right) }}, \\ {\nu }_{21}^{\left( k \right) }= & {} \frac{{\nu }_{12}^{\left( k \right) }E_{22}^{\left( k \right) }}{E_{11}^{\left( k \right) }}, \\ \bar{q}_{31}= & {} q_{31}\cos ^{2}\theta + q_{32}\sin ^{2}\theta , \bar{q}_{32} = q_{32}\cos ^{2}\theta + q_{31}\sin ^{2}\theta , \\ \bar{q}_{14}= & {} \left( q_{15}-q_{24} \right) \sin \theta \cos \theta , \bar{q}_{24} = q_{24}\cos ^{2}\theta + q_{15}\sin ^{2}\theta , \\ \bar{q}_{15}= & {} q_{15}\cos ^{2}\theta + q_{24}\sin ^{2}\theta , \bar{q}_{25} = \left( q_{15}-q_{24} \right) \sin \theta \cos \theta , \\ \bar{q}_{36}= & {} \left( q_{31}-q_{32} \right) \sin \theta \cos \theta , \end{aligned}$$

where $E_{i}$, $v_{ij}$ and $G_{ij}$ are, respectively, Young’s moduli, Poisson’s ratios and shear moduli.

Appendix B

The coefficients $\hat{S}_{ij}$, $\hat{M}_{ij}$ and $\hat{C}_{ij}$ ($i=1,2,3)$ appeared in Eq. (24) can be obtained as

$$\begin{aligned} \hat{S}_{11}= & {} D_{11}\left( \frac{n\pi }{a} \right) ^{4} + D_{22}\left( \frac{m\pi }{b} \right) ^{4} + \left( 2D_{12}\mathrm {+4}D_{66} \right) \left( \frac{n\pi }{a} \right) ^{2}\left( \frac{m\pi }{b} \right) ^{2} + K_{\mathrm{W}} + K_{\mathrm{P}}\left[ \left( \frac{n\pi }{a} \right) ^{2} + \left( \frac{m\pi }{b} \right) ^{2} \right] , \\ \hat{S}_{12}= & {} - E_{11}^{1}\left( \frac{n\pi }{a} \right) ^{3}-\left( E_{21}^{1}\mathrm {+2}E_{66}^{1} \right) \frac{n\pi }{a}\left( \frac{m\pi }{b} \right) ^{2}, \\ \hat{S}_{13}= & {} - E_{22}^{1}\left( \frac{m\pi }{b} \right) ^{3}-\left( E_{12}^{1}\mathrm {+2}E_{66}^{1} \right) \left( \frac{n\pi }{a} \right) ^{2}\frac{m\pi }{b}, \\ \hat{S}_{22}= & {} E_{11}^{3}\left( \frac{n\pi }{a} \right) ^{2} + E_{66}^{3}\left( \frac{m\pi }{b} \right) ^{2} + E_{55}^{3}, \\ \hat{S}_{23}= & {} \left( E_{12}^{3} + E_{66}^{3} \right) \frac{n\pi }{a}\frac{m\pi }{b}, \\ \hat{S}_{33}= & {} E_{66}^{2}\left( \frac{n\pi }{a} \right) ^{2} + E_{22}^{3}\left( \frac{m\pi }{b} \right) ^{2} + E_{44}^{3}, \\ \hat{M}_{11}= & {} \beta _{31}\left( \frac{n\pi }{a} \right) ^{2} + \beta _{32}\left( \frac{m\pi }{b} \right) ^{2}, \hat{M}_{21} = \gamma _{31}\frac{n\pi }{a}, \hat{M}_{31} = \gamma _{32}\frac{m\pi }{b}, \\ \hat{M}_{12}= & {} \hat{M}_{13} = \hat{M}_{22} = \hat{M}_{23} = \hat{M}_{32} = \hat{M}_{33}=0, \\ \hat{C}_{11}= & {} I_{2}\left[ \left( \frac{n\pi }{a} \right) ^{2} + \left( \frac{m\pi }{b} \right) ^{2} \right] + I_{0}, \hat{C}_{12} = - I_{e}\frac{n\pi }{a}, \hat{C}_{13} = - I_{e}\frac{m\pi }{b}, \\ \hat{C}_{22}= & {} I_{e}^{2}, \hat{C}_{23}=0,\hat{C}_{33} = I_{e}^{2}. \end{aligned}$$