Vibration performance of a vertical conveyor system under two simultaneous resonances

Abstract

This study focused on the vibration behavior of a modified vertical conveyor system. The calculated system is exhibited by 2-degree-of-freedom counting quadratic and cubic nonlinearities among both external and parametric forces. Technique of multiple scales connected to gain approximate solutions and study stability of measured structure. All resonances from mathematical solution are extracted. The performance of the system is measured by means of Runge–Kutta fourth-order process (e.g., ode45 in MATLAB). Moreover, two simultaneous resonance cases of this system have been studied analytically and numerically. Stability of acquired numerical solution discovered via frequency response equations. Influences contained by important coefficients scheduled frequency response curves of the considered structure are studied inside numerical results. Methodical results obtained in this work agreed well through the numerical outcome. The description outcome is matched up to available recently published articles.

Appendix A

Starting Ref. [5] as:

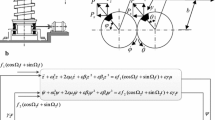
Equations of action for vertical shaking conveyor can be gained applying subsequently Lagrange’s equation

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( {\frac{\partial T}{\partial \dot{q}_i }} \right) +\frac{\partial D}{\partial \dot{q}_i }-\frac{\partial T}{\partial q_i }+\frac{\partial V}{\partial q_i }=Q_i \end{aligned}$$

(A.1)

where $q_i$ is the generalized coordinate, $Q_i$ be generalized force, and T is kinetic energy specified as

$$\begin{aligned} T=\frac{1}{2}m\dot{z}^{2}+\frac{1}{2}I_z \dot{\psi }^{2} \end{aligned}$$

(A.2)

where m is the mass of the trough of the conveyor, $I_z$ is the inertia moment of the conveyor about vertical axis, and V the potential energy, is known through

$$\begin{aligned} V=\frac{1}{2}k_1 z^{2}+\frac{1}{3}k_2 z^{3}+\frac{1}{4}k_3 z^{4}+\frac{1}{2}k_{t1} \psi ^{2}+\frac{1}{3}k_{t2} \psi ^{3}+\frac{1}{4}k_{t3} \psi ^{4} \end{aligned}$$

(A.3)

where z and $\psi$ are the vertical and angular positions of the trough, $k_1$, $k_2$, $k_3$, $k_{1t}$, $k_{2t}$, $k_{3t}$ are the linear, and nonlinear spring constants of the vertical and angular springs, respectively, and D be the Rayleigh dissipation function, is specified as

$$\begin{aligned} D=\frac{1}{2}c\dot{z}^{2}+\frac{1}{2}c_t \dot{\psi }^{2} \end{aligned}$$

(A.4)

where c and $c_t$ are the dumping constants of the vertical and angular springs, respectively. Purpose of Lagrange’s equation for two coordinates $q_1 =z$ and $q_2 =\psi$ provides the next differential equations of motion

$$\begin{aligned}&m\ddot{z}+c\dot{z}+k_1 z+k_2 z^{2}+k_3 z^{3}=\sum {P_z } \end{aligned}$$

(A.5)

$$\begin{aligned}&I_z \ddot{\psi }+c_B \dot{\psi }+k_{t1} \psi +k_{t2} \psi ^{2}+k_{t3} \psi ^{3}=\sum {M_z } \end{aligned}$$

(A.6)

where $\sum {P_z }$ is the total force of these four unbalanced masses, and $\sum {M_z }$ is the total moment of these forces about the axes of the conveyor. These four disks might be rotated synchronously in order to construct same angle as that between the unbalanced masses on the crossing disks in Fig. 1a. This situation is providing by the gears. The total force of these four unbalanced masses is calculated like

$$\begin{aligned} \sum {P_z } =2P\left( {\cos \theta +\sin \varphi } \right) \end{aligned}$$

(A.7)

The total moment about the axes of the conveyor of these forces is also computed as

$$\begin{aligned} \sum {M_z } =2Pb\left( {\cos \varphi +\sin \theta } \right) \end{aligned}$$

(A.8)

The angle $\theta$ is equal to $\varphi$ if the angles of unbalanced masses on the same side of the axes of disks are taken as equal, and the angle on the opposite side is $90^{^{\circ }}$. The force due to the inertia of unbalanced masses applied toward the system is printed as

$$\begin{aligned} P=m_0 r_0 \Omega ^{2} \end{aligned}$$

(A.9)

where $m_0$, $r_0$, $\Omega$ are the unbalanced mass, radius of the unbalanced mass and angular frequency of the unbalanced mass, respectively. Besides, if disks are assumed to rotate with a constant angular velocity, $\varphi$ and $\theta$ can be written as

$$\begin{aligned}&\varphi =\Omega _1 t \end{aligned}$$

(A.10)

$$\begin{aligned}&\theta =\Omega _2 t \end{aligned}$$

(A.11)

Then (A.7) and (A.8) can be computed as

$$\begin{aligned}&\sum {P_z } =2m_0 r_0 \Omega ^{2}\left( {\cos \Omega _1 t+\sin \Omega _1 t} \right) \end{aligned}$$

(A.12)

$$\begin{aligned}&\sum {M_z } =2m_0 r_0 \Omega ^{2}b\left( {\cos \Omega _2 t+\sin \Omega _2 t} \right) \end{aligned}$$

(A.13)

Substituting (A.12) and (A.13) into (A.5) and (A.6), we obtain vertical and angular movement equations of the vertical conveyor as

$$\begin{aligned}&m\ddot{z}+c\dot{z}+k_1 z+k_2 z^{2}+k_3 z^{3}=2m_0 r_0 \Omega ^{2}\left( {\cos \Omega _1 t+\sin \Omega _1 t} \right) \end{aligned}$$

(A.14)

$$\begin{aligned}&I_z \ddot{\psi }+c_B \dot{\psi }+k_{t1} \psi +k_{t2} \psi ^{2}+k_{t3} \psi ^{3}=2m_0 r_0 \Omega ^{2}b\left( {\cos \Omega _2 t+\sin \Omega _2 t} \right) \end{aligned}$$

(A.15)

Dividing (A.14) by m and (A.15) by $I_z$, we will attain the subsequent equations:

$$\begin{aligned}&\ddot{z}+\frac{c}{m}\dot{z}+\frac{k_1 }{m}z+\frac{k_2 }{m}z^{2}+\frac{k_3 }{m}z^{3}=\frac{2m_0 r_0 \Omega ^{2}}{m}\left( {\cos \Omega _1 t+\sin \Omega _1 t} \right) \end{aligned}$$

(A.16)

$$\begin{aligned}&\ddot{\psi }+\frac{c_B }{I_z }\dot{\psi }+\frac{k_{t1} }{I_z }\psi +\frac{k_{t2} }{I_z }\psi ^{2}+\frac{k_{t3} }{I_z }\psi ^{3}=\frac{2m_0 r_0 \Omega ^{2}b}{I_z }\left( {\cos \Omega _2 t+\sin \Omega _2 t} \right) \end{aligned}$$

(A.17)

Equations (A.16) and (A.17) can be lastly printed as

$$\begin{aligned}&\ddot{z}+\omega _1^2 z+2\mu _1 \dot{z}+\beta _1 z^{2}+\beta _2 z^{3}=f_1 (\cos \Omega _1 t+\sin \Omega _1 t) \end{aligned}$$

(A.18)

$$\begin{aligned}&\ddot{\psi }+\omega _2^2 \psi +2\mu _2 \dot{\psi }+\beta _3 \psi ^{2}+\beta _4 \psi ^{3}=f_2 (\cos \Omega _2 t+\sin \Omega _2 t) \end{aligned}$$

(A.19)

Then we modified theses equations as presented inside this manuscript in Eq. (1).