Abstract
This paper is a contribution to our understanding of the technical concept of given in Greek mathematical texts. By working through mathematical arguments by Menaechmus, Euclid, Apollonius, Heron and Ptolemy, I elucidate the meaning of given in various mathematical practices. I next show how the concept of given is related to the terms discussed by Marinus in his philosophical discussion of Euclid’s Data. I will argue that what is given does not simply exist, but can be unproblematically assumed or produced through some effective procedure. Arguments by givens are shown to be general claims about constructibility and computability. The claim that an object is given is related to our concept of an assignment—what is given is available in some uniquely determined, or determinable, way for future mathematical work.















Similar content being viewed by others
Notes
Greek philosophical texts, on the other hand, do speak in this more general way. See, for example, Proclus’ discussion of the parts of a proposition (Friedlein 1873, 203–205).
Here I mean “problem” as a unit of mathematical text that can be contrasted with a “theorem.” In Greek mathematical discourse, solving a problem generally means doing what one set out to do, and this is usually expressed by saying that the problem has been done, or produced.
Fournarakis and Christianidis (2006)—contrary to almost all other scholars—argue that there is a meaningful distinction between the perfect and aorist participles of
 that has both philosophical and mathematical implications. I do not see that this difference has, however, any meaning for the mathematical practice. Acerbi points out that, in the Data, finite verb forms are also used with what appears to be the same meaning, and he gives statistics for the occurrences of the various forms of the particle in canonical authors (Acerbi 2011a, 122, 127). In other authors, we also have a range of usage of finite verbs and particles. I cannot see any mathematically meaningful distinction between the different forms and I am dubious of our ability to propose emendations to the received manuscripts along these lines.
that has both philosophical and mathematical implications. I do not see that this difference has, however, any meaning for the mathematical practice. Acerbi points out that, in the Data, finite verb forms are also used with what appears to be the same meaning, and he gives statistics for the occurrences of the various forms of the particle in canonical authors (Acerbi 2011a, 122, 127). In other authors, we also have a range of usage of finite verbs and particles. I cannot see any mathematically meaningful distinction between the different forms and I am dubious of our ability to propose emendations to the received manuscripts along these lines.Diophantus’ use of given and the related concepts of posited, sought, found, determined and so on, in both Arithmetics and Polygonal Numbers is rather involved and, consequently, I will put off examining these texts for another time.
For example, a line that falls at a given angle on two parallels given in position.
For example, Marinus states that those who believe that what is given by hypothesis—which he also calls “the exposited (
 ) in the hypothesis of the problem”—is the given are mistaken (Menge 1896, 248, 236). He may be talking to his teacher in this passage. Proclus, in his discussion of the parts of a proposition, claims that in Elem. IV.10 nothing is given, because nothing is stated to be given in the enunciation and there is no exposition (Friedlein 1873, 203–204). But Proclus is wrong here. Although nothing is stated to be given, the construction of Elem. IV.10 begins by setting out an arbitrary line, AB, and an understanding of the practice in the Elements and Data makes it clear that when an arbitrary line segment is set out in a construction, it is set out as given in position and in magnitude. Hence, Elem. IV.10, in fact, shows us how to construct an isosceles triangle that has as one of its equal sides as a given line, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\). That is, although the Elem. IV.10 makes no mention of an object given in the sense of \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), there is an object given in the sense of \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\). Thus, although Marinus is correct that there is no logical difference between \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), we could ask for an isosceles triangle whose base is a given line, \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), which would be a different problem. This highlights the practical difference between \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\)—namely the enunciation of Elem. IV.10 leaves us free to set out a given line as either a leg or the base, so that the constraints of the problem, \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), leave us free in our choice of the line given in the sense of \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\). Acerbi (2011a, 121), following Marinus, takes \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\) to be the same.
) in the hypothesis of the problem”—is the given are mistaken (Menge 1896, 248, 236). He may be talking to his teacher in this passage. Proclus, in his discussion of the parts of a proposition, claims that in Elem. IV.10 nothing is given, because nothing is stated to be given in the enunciation and there is no exposition (Friedlein 1873, 203–204). But Proclus is wrong here. Although nothing is stated to be given, the construction of Elem. IV.10 begins by setting out an arbitrary line, AB, and an understanding of the practice in the Elements and Data makes it clear that when an arbitrary line segment is set out in a construction, it is set out as given in position and in magnitude. Hence, Elem. IV.10, in fact, shows us how to construct an isosceles triangle that has as one of its equal sides as a given line, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\). That is, although the Elem. IV.10 makes no mention of an object given in the sense of \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), there is an object given in the sense of \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\). Thus, although Marinus is correct that there is no logical difference between \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), we could ask for an isosceles triangle whose base is a given line, \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), which would be a different problem. This highlights the practical difference between \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\)—namely the enunciation of Elem. IV.10 leaves us free to set out a given line as either a leg or the base, so that the constraints of the problem, \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), leave us free in our choice of the line given in the sense of \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\). Acerbi (2011a, 121), following Marinus, takes \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\) to be the same.A clear example of this is Ptolemy’s claim that the theorems he sets out in Alm. I.10 can be used to compute the entries in the chord table “by means of lines” (
 ) despite his later claim that \(\text {Crd}(1/2{^{\circ }})\) “is not given in any way by means of lines” (
) despite his later claim that \(\text {Crd}(1/2{^{\circ }})\) “is not given in any way by means of lines” ( ), because it is \(\text {Crd}(11/2{^{\circ }}\div 3)\), where \(\text {Crd}(11/2{^{\circ }})_m\) is given (Heiberg 1898–1903, I.31–32, I.42). Indeed, in the derivation of the chord table, Alm. I.10, the metrical analyses treat \(\text {Crd}(1/2{^{\circ }})\) as given, despite the fact that he has claimed that it is not given “by means of lines.” That is, once the value of this chord has been determined as given, \(\mathbf{(G}_\mathbf{3}{} \mathbf{)}\), through his approximation technique it can be taken as given, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), in a new procedure.
), because it is \(\text {Crd}(11/2{^{\circ }}\div 3)\), where \(\text {Crd}(11/2{^{\circ }})_m\) is given (Heiberg 1898–1903, I.31–32, I.42). Indeed, in the derivation of the chord table, Alm. I.10, the metrical analyses treat \(\text {Crd}(1/2{^{\circ }})\) as given, despite the fact that he has claimed that it is not given “by means of lines.” That is, once the value of this chord has been determined as given, \(\mathbf{(G}_\mathbf{3}{} \mathbf{)}\), through his approximation technique it can be taken as given, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), in a new procedure. is a technical expression in Ptolemy’s writings (Heiberg 1898–1903, I.32, 42, 251, 335, 380, 383, 416, 449; II.193, 198, 201, 210, 321, 426, 427, 429; Heiberg 1907, 202, 203). It designates either a metrical analysis or an actual calculation—either through elementary geometry or chord-table trigonometry.
is a technical expression in Ptolemy’s writings (Heiberg 1898–1903, I.32, 42, 251, 335, 380, 383, 416, 449; II.193, 198, 201, 210, 321, 426, 427, 429; Heiberg 1907, 202, 203). It designates either a metrical analysis or an actual calculation—either through elementary geometry or chord-table trigonometry.The construction of the conic sections in both the analysis and the synthesis appears to produce the curves using a locus definition, for which we have no corresponding problem in the extant elementary treatises, including the Conics.
The function of these different constructions will become clearer in Sect. 4.
These lines may also be given in position as well, but that is not essential to the argument.
Acerbi (2011a, 139) also emphasizes this point.
In the text, we are simply told that the line is laid out “in position” (
 ), but this is the standard expression by ellipsis for given in position, often used in Euclid’s Data and probably in Apollonius’ Cutting off a Ratio. As just one example, see Data 43 , Sect. 3.3.
), but this is the standard expression by ellipsis for given in position, often used in Euclid’s Data and probably in Apollonius’ Cutting off a Ratio. As just one example, see Data 43 , Sect. 3.3.Furthermore, the point D is not explicitly said to be given in position, but \(DH_p\) is said to terminate at D, and will we see in the argument that follows that we do, in fact, assume \(d_p\) as given in position. Hence, the claim that line \(DH_p\) is terminating at D must be read to mean that point \(d_p\) is given. This is essentially the same as the initial constructive step of Elem. I.22.
It is a common practice to assume points and lines as given in position—see, for example, Data 28, 40–43, 55.
Some scholars want to avoid the claim that we must assume the existence of these objects by arguing that we are simply assuming a potential configuration. In this case, however, it is only their existence as lines having a certain mathematical constraint that is of any importance—their configuration is irrelevant.
This “directionality” of the argument by givens is crucial. It begins with the objects asserted as given in the enunciation of the problem itself, \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), not with the objects assumed in the analytical assumption—unless those later objects are assumed to be equal to the originally given objects. This makes it clear that Acerbi (2011a, 139) is incorrect in his assessment of the starting point of the resolution of Conics II.50. He claims that \(\angle \hbox {B}\Delta \Gamma \) is given because it is equal to another angle, and that it is irrelevant that this other angle is given. But the fact that this other angle is given is absolutely essential. In fact, \(\angle \hbox {B}\Delta \Gamma \) \(=\angle \hbox {EZH}_m\) is a key part of the analytical assumption, while \(\angle \hbox {EZH}_m\) being given in magnitude is one of the conditions of the problem. That is, what it means to assume that \(\angle \hbox {EZH}_m\) is given in the statement of the problem is that we assume that another angle, say \(\angle \hbox {B}\Delta \Gamma \), can be produced equal to it. Then, \(\angle \hbox {B}\Delta \Gamma _m\) is also given by Data Def. 1, because we can construct another angle equal to it—namely any angle equal to \(\angle \hbox {EZH}_m\). (See the discussion of Data Def. 1, Sect. 3.1.) The location of \(\angle \hbox {B}\Delta \Gamma _m\) is not yet relevant, but it will shortly be proven to be given in position. In order to start the resolution, however, all we need is to know that we can produce somewhere on line \(\hbox {B}\Delta \) an angle equal to \(\angle \hbox {EZH}_m\)—which, of course, can actually be done with Elem. I.23. The logical force of this “directionality” is also why the false arguments advanced by Berggren and Van Brummelen (2000, 25–26) that use Data 2 to show that the side of a square that is equal to a given circle is given, or that the third of a given angle is given, are not successful as analytical resolutions.
It is clear from the problems of the Elements and the theorems of the Data, that the assumption of points and lines as given was taken for granted. For points, see, for example, Elem. I.9, 11, 23, Data 32, 33, 37, 38. The case for lines can be seen in Elem. I.22, Data 39–43. That the points and lines set out in the problem-constructions of the Elements must be considered as given can be shown from the fact that they serve as the basis for further constructions that are performed through problems that themselves assume as given these very points and lines.
See Dijksterhuis (1987, 58) for a derivation of the symptoma from what is believed to be the pre-Apollonian construction of the conic section.
That is, taking \(z\,^{\prime }_p\) as given, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), we would have \(\mathbf {R}(a_m,dz\,^{\prime }_m\,)_m\) as given, by Data 26 and 52, so that \(\mathbf {S}(zQ\,)_m\) is given by Data Def. 1. Then, by Data 55, line \(zQ\,^{\prime }_m\) is given. And since \(\angle dz\,^{\prime }Q\,^{\prime }\) is right on line \(dH_p\) given in position, locally \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), line \(z\,^{\prime }Q\,^{\prime }_p\) is given in position, by Data 29, so that point \(q\,^{\prime }_p\) is given, \(\mathbf{(G}_\mathbf{3}{} \mathbf{)}\), by Data 27.
That is, taking \(z\,^{\prime }_p\) as given, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), we would have \(dz\,^{\prime }_m\) as given, by Data 26, so that \(z\,^{\prime }q\,^{\prime }_m\) is given, by Data 57. And, again, And since \(\angle dz\,^{\prime }Q\,^{\prime }\) is right on line \(dH_p\) given in position, locally \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), line \(z\,^{\prime }Q\,^{\prime }_p\) is given in position, by Data 29, so that point \(q\,^{\prime }_p\) is given, \(\mathbf{(G}_\mathbf{3}{} \mathbf{)}\), by Data 27.
See Sect. 3.
In fact, there are substantial issues with Conics II.4, which seems simply to reduce the problem to a different problem. Also, notice, that the parabola required for Menaechmus’ problem is produced by Conics I.52, but not by Conics VI.31, which may help us understand the difference between those two problems; see also the discussion of this issue by Fried and Unguru (2001, 264–268).
Vitrac (2005, 40–42) gives a discussion of the context in which Menaechmus and his circle argued for the primacy of problems.
Very nearly every step in the Data can be justified by a proposition, definition or postulate, either from earlier in the Data itself, or from Elements I–VI. The few exceptions require lemmas that can themselves be demonstrated using only Elements I–VI and the Data, such as in Data 24 and 67, or are corollaries of a definition, such as Data 25–30 (see note 28).
Data 25–29 are corollaries of Data Def. 4, the proofs of which simply involve pointing out that if they do not hold the consequence is contrary to the definition. Data 30 shows a contradiction with Elem. I.16, but it also depends on the assumption that Data Def. 4 does not hold.
Taisbak (2003, 32–33) points out that Data Def. 2 must often be read to mean that both of the terms of the instantiated ratio are themselves given.
See the commentary to Data 2, Sect. 3.2.
This restriction does not apply to objects introduced in theorems and in the demonstrations of problems, which do not need to be constructible through an effective procedure.
See note 28, above.
Here, I use “distance” as a translation of the Greek term
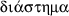 , the span with which a circle is drawn (Sidoli 2004b).
, the span with which a circle is drawn (Sidoli 2004b).Friberg (2007, 211–234) gives a recent reading of the enunciations of select theorems of the text along these lines.
Doubt has been expressed about whether or not angles can be considered to be magnitudes—largely because the definition of ratio in the Elements, Elem. V.def.4, cannot apply to the conception of angles in Greek geometrical texts as always being less than 180°. Among modern scholars, see for example Artmann (1999, 123) and Taisbak (2003, 23, 30). Rashed (2015) has provided a thorough study of various approaches taken to this topic by ancient and medieval scholars. Whatever the reservations that might be advanced, however, some of the propositions in the first part of the Data must be used to justify claims that angles are given in magnitude in the rest of the treatise, so angles must be included in this general treatment of given magnitudes. Moreover, Greek mathematicians worked with ratios between angles in practice, and applied theorems from Elements V to proportions resulting from such ratios. Hence, they were either willing to overlook the failure of Elem. V.def.4 to apply to angles or they regarded this definition as of use to the local foundational issues of Elements V but not as sufficient to invalidate the clear utility of working with ratios and proportions among angles—particularly, when represented by numerical values.
Data Def. 1.
Data Def. 2.
Elem. V.16.
Data Def. 1.
That is, \(de_{m,p}\) is assumed to be given in magnitude and in position, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\).
Elem. III.33.
Data Def. 8. Of course, there are two semicircles that could have been produced on \(DE_{m,p}\), but we are only concerned with the one that is actually produced.
This is the production of Z as a fourth proportional through Data Def. 2.
Data Def. 2, since there is a procedure for producing lines in the same ratio.
Data 2.
GB is the hypotenuse.
Elem. V.def.5.
Elem. IV.1. As Taisbak (2003, 128) points out, the construction for inserting line DH involves producing the same circle about center D with distance DH that will be explicitly introduced two steps later. But this “repeated construction” follows the conventions of constructions in Euclid’s problems. Whenever an object in invoked using a previously established problem, only the object itself is produced. Any auxiliary objects that may have been involved in its construction are not available for further work and have to be produced independently if they are needed—as is done here.
Elem. I.post.1.
Elem. I.post.3. See note 34, above, for my choice to use “distance.”
Data Def. 6.
Data 25.
Data 26.
Data 1, Def. 1 and Def. 3.
Elem. VI.7.
Data Def. 3.
It might appear that this can be done through Elem. VI.12, but this problem requires that we have three given lines, not merely one given line and a given ratio. If we consider the bundles of parallel lines discussed in Sect. 3.2, above, we can see an example of how this construction could actually be carried out with only one given line—all of which is simply taken as a primitive concept in Data Def. 2.
Notice that the only theorems of the Data that are applied in the argument that \(\mathbf {T}(deh)_{f,m,p}\) is fully given are Data 25 and 26, which are simply reiterations of Data Def. 4. That is, \(\mathbf {T}(deh)_{f,m,p}\) is fully given because it was so constructed, by the definition, and implications, of the concept of given in position. Hence, a figure whose points are given in position is fully given.
This is clear from the way right angles are treated in the Data. Acerbi (2011a, 123) gives an explanation for why this is so, based on the construction of right angles.
Proponents of the strong form of the geometrical algebra interpretation of Elements II, VI and Data 57–60 and 84–85—namely, the claim that certain propositions in these texts were motivated by a desire to justify arithmetical problem-solving techniques—must contend with the fact that this highly geometrical, and frankly rather peculiar, proposition is the only candidate in the text for propositions demonstrating that the product of two given numbers is given. This strong interpretation of the hypothesis of geometrical algebra is the claim GA2 set out by Blåsjö (2016, 326). His GA1 is simply another way talking about the theory of the application of areas, which is not in any dispute. For example, Dijksterhuis (1987, 51–52), who developed a notation for expressing the theory of the “Application of Areas” in a symbolic form that is both true to the original conception and reflects the abstract operational nature of the theory, refers to it also as “Geometrical Algebra” only the first time he introduces his terminology in order to alert the reader to the fact that he will use these symbols to treat what Zeuthen (1885, 7) had called geometrical algebra. Dijksterhuis (1987, 7) presumably preferred his own symbolism and the terminology “application of areas” because, as he says, “in a representation of Greek proofs in the symbolism of modern algebra it is often precisely the most characteristic qualities of the classical argument that are lost.”
Taisbak (2003, 139, n. 105) has pointed out the strangeness of speaking of a “form given in form” (
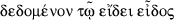 ). Data Def. 3 construes given in form as applying to rectilinear figures, and the proof of this proposition makes it clear that the “form” we are dealing with here is, in fact, a rectilinear figure.
). Data Def. 3 construes given in form as applying to rectilinear figures, and the proof of this proposition makes it clear that the “form” we are dealing with here is, in fact, a rectilinear figure.Elem. I.46.
Data Def. 3 and 1. The argument for this is detailed below. Taisbak (2003, 139, n. 106, 151, n. 110, 90–91), suggests that there is some circularity in this argument with Data 55 and, through two notes, refers the reader back to his commentary to Data 24 for this step, where he shows, for example, that \(a_m, b_m \Rightarrow \) \(\mathbf {R}(a_m,b_m)_m\) and \(\mathbf {S}(A\,)_m \Rightarrow a_m\). But the inference required for this proposition is \(a_m \Rightarrow \mathbf {S}(a_m)_m\), which, he correctly notes, follows directly from Elem. I.46, Data Def. 3 and 1—as I will flesh out below.
Data 49.
Data 2.
As Taisbak (2003, 139) has observed, this theorem could have been based directly on Data Def. 1, by constructing another figure equal to \(\mathbf {F}(ABGDE{\dots })_f\). This construction, however, would be no simpler than that of the square, and it would not explicitly relate the figure to a known square, which was presumably a goal of Euclid’s proof.
We will see an example of this in Sect. 4.
This problem is also discussed by Zheng (2012, 140–142), but he does not fully articulate the use of the propositions of the Data in the resolution—perhaps because he follows the translation of Decorps-Foulquier and Federspiel (2008–2010, 2.3.93), who do not provide justifications for the steps of the resolution of this analysis–synthesis pair.
This is the analytical assumption.
This is a purely hypothetical construction, because there is no problem in the Conics that shows how to produce ordinates—that is, parallel lines bisected by the diameter. See note 81.
Elem. 1.post.2.
Conics I.def.4.
These lines are simply assumed as given parallels, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\). As often, however, this can be reduced the assumption of points given in position. This is fleshed out in the commentary below.
Data 25, 26, 7 and 27 (see commentary below).
Data 26.
Elem. I.post.1, I.31.
Elem. I.10, twice.
Elem. I.posts.1, Conics I.def.4.
Point G is specified as the intersection of the conic section and the diameter simply by the fact that it occurs in both of these names.
In fact, ordinates would most simply be produced by drawing parallels to a tangent to the conic section, but tangents are produced in Conics II.49–51 and 53, which have yet to be established.
That a line intersecting a given object, \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), can be taken as given in position, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), is made clear in a number of propositions, such as Elem. III.1, Data 24, and 39, but see also the discussion by Taisbak (2003, 25). This is, of course, reducible to the assumption of two points, \(b_p\) and \(d_p\), given in position, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), joined by a line, Elem. I.post.1.
That an arbitrary point can be taken as given, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), on a line given in position, \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), is seen in its implicit use in Elem. I.9, I.11, Data 32–33, and 37–38, and so on.
Heath (1921, I.423) makes a similar point in his summary of the Data.
Acerbi (2007, 512–519) has discussed this type of reasoning in texts by Heron, Ptolemy and Diophantus. I have elsewhere analyzed the metrical analysis by Theon of Smyrna (Sidoli Forthcoming a).
This type of argument is called an “analysis” by Heron throughout his Measurements, and by Pappus in his commentary on Ptolemy’s Almagest V (Rome 1931–1943, 35). I have not found a passage where Ptolemy himself refers to this type of argument as an “analysis.” In fact, Ptolemy refers to his articulation of metrical analysis in the style of Heron as a “theorem” (Heiberg 1898–1903, 38, 40).
I originally introduced the term metrical analysis as a category to discuss Ptolemy’s practice and simply noted in passing the similarities between these types of arguments in Heron and Ptolemy (Sidoli 2004a, 17–19). I have elsewhere discussed the role of this type of argument with respect to mathematical tables in the Almagest (Sidoli 2014, 25–26). See also the discussion by Acerbi (2012, 201–208).
Acerbi and Vitrac (2014, 363–409) provide a complete analysis of Heron’s use of arguments by “chains of givens” and their relationship to computational algorithms. In this section, I give one example and develop a symbolic representation of Heron’s practice.
For our purposes here, we will ignore the argument concerning the fourth side.
Elem. I.10.
Elem. I.31.
Elem. I.post.2.
Elem. I.15 and 26.
That is, \(DZ+(AD+BH\,)=HG+(AD+BH\,)\).
Elem. I.c.n.2, since \(AZ=DZ+AD\) and \(BG=HG+BH\).
Data 3, and by assumption, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\).
Data Def. 1.
Elem. I.33.
Data 7.
By assumption, \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\).
Heron is using
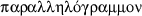 to mean rectangle. This is not uncommon in Greek mathematical texts. For example, Archimedes also employs the term in this way (Heiberg and Stamatis 1972, II.418, 426, 428).
to mean rectangle. This is not uncommon in Greek mathematical texts. For example, Archimedes also employs the term in this way (Heiberg and Stamatis 1972, II.418, 426, 428).Data 52.
That is, \(\mathbf {T}(DEZ\,)+\mathbf {Pent}(ABHED\,)=\mathbf {T}(EHG\,)+\mathbf {Pent}(ABHED\,)\).
Elem. I.c.n.2.
Data Def. 1.
One of the conditions of Data 52 also stipulates that the figure must be given in form, but, of course, \(\mathbf {Trap}(ABGD)\) meets this condition.
Heron’s use of this type of reasoning is also discussed by Acerbi (2011a, 143–144; 2012, 201–204).
See Christianidis and Oaks (2013) for study of Diophantus’ problem-solving techniques.
This is not always the case in the computations that correspond to metrical analysis. Sometimes a computed number can be taken up some steps later—as we will see below in the example drawn from Ptolemy.
The Almagest can be divided into units of text based on the types of mathematical argument involved. Alm. III.5.1 is a chord-table trigonometric computation that is followed by Alm. III.5.2 (I.241.14–242.24) and Alm. III.5.3 (I.243.1–243.15), which are both metrical analyses.
Alm. III.5.1 (I.241.1–242.13) uses chord-table trigonometry to compute \(\alpha = 1{;}9{^{\circ }}\) and \(\kappa =28{;}51{^{\circ }}\), where \(\bar{\kappa }\) is explicitly asserted to be given as 30\({^{\circ }}\), and \((e{:}r)_r\) is treated as the pair of numbers \(2;30^{\mathrm {p}}\) and \(60^{\mathrm {p}}\).
Elem. I.12.
That is, arc \(AB_m :=\kappa \).
Data 40, Def. 3.
Namely \((DQ:QZ\,)_r :=(e:r,)_r=(2;30^\text {P}:60^\text {P})\), as shown in Alm. III.4.
Data 8.
Data 43.
That is, the equation of anomaly, \(\angle QZL_m :=\alpha \).
That is arc \(EZ_m :=\bar{\kappa }\), by Elem. I.32 and Data 4. or Data 3
The strategy of the proof of Data 40 is essentially the same as that for Data 43. See Sect. 3.3, above.
Ptolemy’s use of this type of reasoning is also discussed by Acerbi (2012, 204–208).
In fact, we could say that this is either given in the sense of \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), because we can set it to whatever value we like, or given in the sense of \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\), because the use of Ptolemy’s chord table, Alm. I.11, always determines this value. This, again, shows the ambiguity between \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\), and reinforces the claim that the function of given is always local.
Or rather with a sort of pseudo-ratio—namely, a length given in terms of another length.
Or rather, entering a chord table with the value of the leg when the hypotenuse has an assumed value.
When we enter into an ancient chord table with a given angle we produce a length given in terms of the hypotenuse—that is, as a pair of numbers, a sort of pseudo-ratio—as is made clear from the fact that Ptolemy always expresses these lengths in terms of a certain hypotenuse. The 120th part of the diameter of the chord table is not understood as a unit in the normal sense, because we divide as many diameters into 120 parts as are required to solve the problem. For this reason, we should not follow Acerbi (2012, 204–208) in rewriting Ptolemy’s text. See also note 142.
Once again we see that the difference between \(\mathbf{(G}_\mathbf{1}{} \mathbf{)}\) and \(\mathbf{(G}_\mathbf{2}{} \mathbf{)}\) is merely local.
Compare, for example, the metrical analysis above with the calculation that proceeds it in Alm. III.5.1. The computation takes 39 lines of Heiberg’s text whereas the metrical analysis takes 9 (Heiberg 1898–1903, 241–243). Moreover, for someone familiar with reasoning by inferences from the Data the metrical analysis given above is trivial and rapid, whereas the computational effort involved in entering even one time into the chord table is rather time consuming for anyone not able to perform sexagesimal computations in their head.
At least by the classical Islamicate period, and probably from much earlier, this blending of the geometrical and arithmetical readings of geometrical books of Euclidean works was commonplace. Thābit ibn Qurra, who knew Euclid’s work as well as anyone, tells us in his Composition of Ratios that although Euclid only defined “quantity” or “magnitude” (
 ) to refer to geometric objects that have “extent” (
) to refer to geometric objects that have “extent” ( ), in his actual works the meaning of the term is broader and refers also to angles, numbers, movements, and so on; and that whenever we read quantity we should also understand number (Lorch 2001, 170; Rashed 2009, 431).
), in his actual works the meaning of the term is broader and refers also to angles, numbers, movements, and so on; and that whenever we read quantity we should also understand number (Lorch 2001, 170; Rashed 2009, 431).A possible exception is the analysis in the final theorem of Diophantus’ Polygonal Numbers.
I will flesh out the details of this in separate paper, focusing on Ptolemy’s use of metrical analysis.
This section of a Diophantine problem has been called the invention and the set up of the equation (Christianidis 2007, 296–298; Christianidis and Oaks 2013, 132–134).
It should be noted that, in general, premodern algebra does not employ the concept of given as part of its problem-solving procedure, but rather uses the practice of assigning actual numbers to stand in as examples of the values that are asserted to be given in the enunciation.
See, for example, the second line of the symbolic representation of the example from Heron above, Section 31.
Blåsjö (2016) has recently made a related argument in regards to the interpretation of certain theorems of Euclid’s Elements as so-called geometrical algebra. He argues, essentially, that this reading has not been definitively refuted. This is, of course, true, but it misses the point. Almost no one would argue that it is not possible to make a reading of Elements I and VI as motivated by and justifying computational problem-solving. The question is rather whether such a reading, or that through the theory of the application of areas, is more broadly successful in explicating the ancient sources.
A possible exception is Diophantus’ Polygonal Numbers, which is essentially arithmetical despite an outward veneer of geometrical language and concepts. (Heath (1921, II.516), for example, states that “the method of proof is strictly geometrical.”)
The vital role of loci and porisms in ancient analysis is elucidated by Knorr (1986) in his brilliant study of ancient geometric problem-solving. See Jones (1986, 547–602) for a summary of the mathematical contents of the lost treatises on porisms and loci. Acerbi (2011a, 137–138, 146–448) discusses the importance of locus theorems and porisms with respect to the language of givens. See also the reconstruction of Euclid’s Porisms by Simpson, which although speculative, can give us a sense for the mathematical concepts involved (Tweddle 2000).
See Edwards (1984, 152–182) for a discussion of the evidence concerning Diodorus. Ptolemy’s use of metrical analysis in Analemma 9 and 10 is described by Edwards in the notes to his translation of these passages.
As is well known,
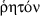 refers to what is precisely expressible in terms of some arbitrary measure, and hence relates to the distinction between what is commensurable and incommensurable—as, for example, in Elements X. Hence, the concept is mathematically related to our notion of a rational number, and the word is sometimes translated in this way. There is a long literature on this material that need not concern us here.
refers to what is precisely expressible in terms of some arbitrary measure, and hence relates to the distinction between what is commensurable and incommensurable—as, for example, in Elements X. Hence, the concept is mathematically related to our notion of a rational number, and the word is sometimes translated in this way. There is a long literature on this material that need not concern us here.For example, the verb
 is used by Apollonius, Conics II.44 to set out a line given in position, as seen above, Sect. 4;
is used by Apollonius, Conics II.44 to set out a line given in position, as seen above, Sect. 4;  is used as a synonym of given in Euclid’s Optics A 18 (Heiberg 1895, 28); and Heron uses
is used as a synonym of given in Euclid’s Optics A 18 (Heiberg 1895, 28); and Heron uses  in Dioptra 13, 14 and elsewhere to mean given (Schöne 1903, 234–236). (The use of
in Dioptra 13, 14 and elsewhere to mean given (Schöne 1903, 234–236). (The use of  by Apollonius in the enunciation and exposition of a number of theorems of the Conics is unrelated to the concept of given. The discussion by Acerbi (2011a, 135) of Apollonius’ usage is obscure to me—it does not introduce something which is “provided,” nor is it used in any problems. It introduces a constructive assumption without which the theorem would not hold—what we can call a contrivance.)
by Apollonius in the enunciation and exposition of a number of theorems of the Conics is unrelated to the concept of given. The discussion by Acerbi (2011a, 135) of Apollonius’ usage is obscure to me—it does not introduce something which is “provided,” nor is it used in any problems. It introduces a constructive assumption without which the theorem would not hold—what we can call a contrivance.)Perhaps this is why Ptolemy, in the metrical analyses of his chord-table trigonometry generally does not speak of a length being given in magnitude, because this would involve him in assigning the same line multiple times. Acerbi (2012, 208) observes this problem of multiple assignments. The end of the metrical analyses in Analemma 9 and 10 support this assessment. In each case Ptolemy first sets the radius of the analemma as given in magnitude and then all the other lengths that he has previously shown to be given in ratio to the radius are all given in magnitude—so that each length has only one assignment.
Lewis’ translation is concerned only with issues relating to surveying, and hence is not reliable with respect to the conventions of Greek mathematical prose, and especially with regards to the use of concepts like given and provided (Lewis 2001, 271–273).
References
Modern Scholarship
Acerbi, F. 2007. Euclide, Tutte le opere. Milano: Bompiani.
Acerbi, F. 2011a. The Language of the ‘Givens’: Its Form and Its Use as a Deductive Tool in Greek Mathematics. Archive for History of Exact Sciences 65: 119–153.
Acerbi, F. 2011b. De Polygonal Numeris, Diofanto. Pisa: Fabrio Serra.
Acerbi, F. 2012. I codici stilistici della matematica greca: dimostrazioni, procedure, algoritmi. Quaderni Urbinati Di Cultura Classica NS 101: 167–214.
Acerbi, F., and B. Vitrac. 2014. Metrica: Héron d’Alexandrie. Pisa: Fabrizio Serra.
Acerbi, F. 2017. The Mathematical Scholia Verera to the Almagest. SCIAMVS 18: 133–259.
Allard, A. 1980. Diophante d’Alexandrie, Les Arithmetiques, Histoire du text grec, édition critique, traductions et scolies. Tourpes: Chercheur du Fonds National Belge de la Recherche Scientifique.
Artmann, B. 1999. Euclid: The Creation of Mathematics. New York: Springer.
Berggren, J.L., and G. Van Brummelen. 2000. The Role and Development of Geometric Analysis and Synthesis in Ancient Greece and Medieval Islam. In Ancient & Medieval Traditions in the Exact Sciences: Essays in Memory of Wilbur Knorr, ed. P. Suppes, J.M. Moravcsik, and H. Mendell, 1–31. Stanford: CSLI Publications.
Blåsjö, V. 2016. In Defence of Geometrical Algebra. Archive for History of Exact Sciences 70: 325–359.
Christianidis, J. 2007. The Way of Diophantus. Historia Mathematica 34: 289–305.
Christianidis, J., and J. Oaks. 2013. Practicing Algebra in Late Antiquity: The Problem-Solving of Diophantus of Alexandria. Historia Mathematica 40: 127–163.
Decorps-Foulquier, M., and M. Federspiel. 2008–2010. Apollonius de Perge, Coniques, Texte grec (et arabe) établi, traduit et commenté, tomes 1.2, 2.3. Berlin: Walter de Gruyter.
Dijksterhuis, E.J. 1987. Archimedes. Princeton: Princeton University Press.
Edwards, D.R. 1984. Ptolemy’s
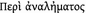 : An Annotated Transcription of Moebeke’s Latin Translation and of the Surviving Greek Fragments, with an English Version and Commentary. PhD Thesis, Department of Classics, Brown University.
: An Annotated Transcription of Moebeke’s Latin Translation and of the Surviving Greek Fragments, with an English Version and Commentary. PhD Thesis, Department of Classics, Brown University.Federspiel, M. 2000. Notes critiques sur le livre II des Coniques d’Apollonius de Perge Seconde partie. Revue des études greques 113: 359–391.
Federspiel, M. 2008. Les problèmes des livres grecs des Coniques d’Apollonius de Perge. Les études classiques 76: 321–360.
Friberg, J. 2007. Amazing Traces of a Babylonian Origin in Greek Mathematics. Singapore: World Scientific.
Fried, M., and S. Unguru. 2001. Apollonius of Perga’s Conica: Text, Context, Subtext. Leiden: Brill.
Friedlein, G. 1873. Procli Diadochi in primum Euclidis Elementorum librum commentarii. Leipzig: Teubner.
Fournarakis, P., and J. Christianidis. 2006. Greek Geometrical Analysis: A New Interpretation Through the ‘Givens’ Terminology. Bollettino di Storia delle Scienze Matematiche 26: 33–56.
Hankel, H. 1874. Zur Geschichte der Mathematik in Alterthum und Mittelalter. Leipzig: Teubner (Reprinted: Olms, Hildesheim, 1965).
Heath, T.L. 1908. The Thirteen Books of Euclid’s Elements, vol. 3. Cambridge: Cambridge University Press (Reprinted: Dover, New York, 1956).
Heath, T.L. 1921. A History of Greek Mathematics, vol. 2. Oxford: Oxford University Press (Reprinted: Dover, New York, 1981).
Heiberg, J.L. 1891–1893. Apollonii Pergaei quae graece extant cum commentariis antiquis. Leipzig: Teubner.
Heiberg, J.L. 1895. Euclidis Optica, Opticorum recensio Theonis, Catoptrica, cum scholiis antiquis. Leipzig: Teubner.
Heiberg, J.L. 1898–1903. Claudii Ptolemaei Syntaxis mathematica. Leipzig: Teubner.
Heiberg, J.L. 1907. Claudii Ptolemaei opera astronomica minora. Leipzig: Teubner.
Heiberg, J.L., and E.S. Stamatis. 1969–1977. Euclidis Elementa, Euclidis opera omnia, vols. 1–5. Leipzig: Teubner.
Heiberg, J.L., and E.S. Stamatis. 1972. Archimedes opera omnia. Stuttgart: Teubner.
Hintikka, J., and U. Remes. 1974. The Method of Analysis: Its Geometric Origin and Its General Significance. Dordrecht: Reidel.
Hughes, B.B. 1981. Jordanus de Nemore: De numeris datis. Berkeley: University of California Press.
Jones, A. 1986. Pappus of Alexandria: Book 7 of the Collection. New York: Springer.
Knorr, W. 1986. The Ancient Tradition of Geometric Problems. Boston: Birkhäuser (Reprinted: Dover, New York, 1993).
Lewis, M.J.T. 2001. Surveying Instruments of Greece and Rome. Cambridge: Cambridge University Press.
Lorch, R. 2001. Thābit ibn Qurra, On the Sector Figure and Related Texts. Islamic Mathematics and Astronomy 108. Frankfurt am Main: Institut für Geschichte der arabisch-islamischen Wissenschaften (Reprinted: Dr. Erwin Rauner Verlag, Augsburg, 2008).
Macierowski, E.M., and R.H. Schmidt. 1987. Apollonius of Perga, On Cutting off a Ratio: An Attempt to Recover the Original Argumentation through a Critical Translation of the Two Extant Medieval Arabic Manuscripts. Fairfield: The Golden Hind Press.
Manitius, K. 1912. Ptolemäus, Handbuch der Astronomie. Leipzig: Teubner (Second edition revised by O. Neugebauer, 1963).
Masià, R. 2015. On Dating Hero of Alexandria. Archive for History of Exact Sciences 69: 231–255.
Mcdowell, G.L., and M.A. Sololik. 1993. The Data of Euclid. Baltimore: Union Square.
Menge, H. 1896. Euclidis Data cum commentario Marini et scholiis antiquis, Euclidis opera omnia, 6. Leipzig: Teubner.
Netz, R. 2000. Why Did Greek Mathematicians Publish Their Analyses? In Ancient & Medieval Traditions in the Exact Sciences: Essays in Memory of Wilbur Knorr, ed. P. Suppes, J.M. Moravcsik, and H. Mendell, 139–157. Stanford: CSLI Publications.
Rashed, R. 1984. Diophante, Les Arithmétiques. Paris: Les Belles Lettres.
Rashed, R. 2008–2010. Apollonius de Perge, Coniques, Texte (grec et) arabe établi, traduit et commenté, tomes 1.1, 2.1, 2.2, 3, 4. Berlin: Walter de Gruyter.
Rashed, R. (ed.). 2009. Thābit ibn Qurra: Science and Philosophy in Ninth-Century Baghdad. Berlin: Walter de Gruyter.
Rashed, R. (ed.). 2015. Angles et grandeur, D’Euclide à Kamāl al-Dīn al-Fārisī. Berlin: Walter de Gruyter.
Rashed, R., and H. Bellosta. 2010. Apollonius de Perge, La section des droites selon des rapports. Berlin: Walter de Gruyter.
Ritter, J. 1989. Chacun se vérité : les mathématiques en Égypte et en Mésopotamie. In Élements d’histoire des sciences, ed. M. Serres. Paris: Bordas.
Ritter, J. 1995. Measure for Measure: Mathematics in Egypt and Mesopotamia. In A History of Scientific Thought, ed. M. Serres. Cambridge, MA: Blackwell.
Rome A. 1931–1943. Commentaires de Pappus et de Théon d’Alexandrie sur l’Almageste, vols. I–III. Biblioteca Apostolica Vatican: Vaticana.
Saito, K., and N. Sidoli. 2010. The Function of Diorism in Ancient Greek Analysis. Historia Mathematica 37: 579–614.
Schöne, H. 1903. Herons von Alexandria, Vermessungslehre und Dioptra, Opera quae supersunt omnia, vol. 3. Leipzig: Tuebner.
Sesiano, J. 1982. Books IV to VIII of Diophantus’ Arithmetica in the Arabic Translation Attributed to Qustā ibn Lūqā. New York: Springer.
Sidoli, N. 2004a. Ptolemy’s Mathematical Approach Applied Mathematics in the Second Century. PhD thesis, University of Toronto, Institute for the History and Philosophy of Science and Technology.
Sidoli, N. 2004b. On the Use of the Term Diastēma in Ancient Greek Constructions. Historia Mathematica 31: 2–10.
Sidoli, N. 2011. Heron of Alexandria’s Date. Centaurus 53: 55–61.
Sidoli, N. 2014. Mathematical Tables in Ptolemy’s Almagest. Historia Mathematica 41: 13–37.
Sidoli, N. Forthcoming a. Mathematical Discourse in Philosophical Authors: Examples from Theon of Smyrna and Cleomedes on Mathematical Astronomy. In Instruments Observations Theories: Studies in the History of Early Astronomy in Honor of James Evans, ed. C. Carman, A. Jones
Souffrin, P. 2000. Remarques sur la datation de la Dioptre d’Héron par l’éclipse de lune du 62. In Autour de le Dioptre d’Héron d’Alexandrie: Actes du Collogue international de Saint-Étienne, ed. G. Argoud and J.-Y. Guillaumin. Saint-Étienne: l’Université Saint-Étienne.
Taisbak, C.M. 1991. Elements of Euclid’s Data. Apeiron 24: 135–171.
Taisbak, C.M. 2003. \({\varDelta }E{\varDelta }OMENA\), Euclid’s Data: The Importance of Being Given. Copenhagen: Museum Tusculanum Press.
Tannery, P. 1893–1895. Diophanti Alexandrini, Opera omnia cum Graecis commentariis. Stuttgart: Teubner.
Thaer, C. 1962. Die Data von Euklid. Berlin: Springer.
Toomer, G.J. 1984. Ptolemy’s Almagest. London: Duckworth (Reprinted: Princeton University Press, Princeton, 1998).
Toomer, G.J. 1990. Apollonius, Conics Books V to VII: The Arabic Translation of the Lost Greek Original in the Version of the Banū Mūsā. New York: Springer.
Toomer, G.J. 1985. Galen on the Astronomers and the Astrologers. Archive for History of Exact Sciences 32: 193–206.
Tweddle, I. 2000. Simpson on Porisms: An Annotated Translation of Robert Simpson’s Posthumous Treatise on Porisms and Other Items on the Subject. London: Springer.
Ver Eecke, P. 1959. Diophante d’Alexandrie, Les six livres Arithmétiques et Le livre des nombres polygones. Paris: Albert Blanchard.
Vitrac, B. 1990–2001. Euclide d’Alexandrie, Les Éléments, vol. 4. Paris: Presses Universitaires de France.
Vitrac, B. 2005. Quelques remarques sur l’usage du mouvement en géométrie dans la tradition euclidienne: de Platon et Aristote à ‘Umar Khayyam. Fahrang: Quarterly Journal of Humanities & Cultural Studies 18: 1–56.
Zeuthen, H.G. 1885. Die Lehre von den Kegelschnitten im Altertum. A.F. Höst & Sohn, 1886 (originally published as “Kegelsnitlaeren in Oltiden,” Kongelig Danske videnskaberens Selskabs Skrifter, 6th ser., 1(3): 1–319).
Zheng, F. 2012. Des Data d’Euclide au De numeris datis de Jordanus de Nemore : Les donneés, l’analyse et les problemes. Thèse de doctorat, Histoire des mathématiques, Université Paris 7, Denis Diderot, Laboratoire SPHERE.
Acknowledgements
The core ideas of this paper go back some years now to my dissertation, and I thank Alexander Jones and Jan Hogendijk for their comments on that work. I presented an overview of this argument at a conference of the SAW Project, under the direction of Karine Chemla. The discussion following this presentation helped me to clarify some of my thinking. During the time that I was a guest of the SAW Project in Paris, 2015, some of the research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007–2013) / ERC Grant Agreement No. 269804. Ken Saito read an earlier draft of this paper and made a number of valuable suggestions. This paper has benefited considerably from the extensive notes made by Karine Chemla and Matthieu Husson.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jeremy Gray.
Ancient Mathematical Works Referenced by Title
Ancient Mathematical Works Referenced by Title
Almagest (Alm.) (properly Mathematical Treatise), Ptolemy: Greek text edited by Heiberg (1898–1903), German translation by Manitius (1912), English translation and corrections by Toomer (1984).
Analemma, Ptolemy: Greek and Latin texts edited by Heiberg (1907, 189–223), Latin text reedited with English translation and commentary by Edwards (1984).
Arithmetics, Diophantus: Greek text edited with Latin translation by Tannery (1893–1895), French translation by Ver Eecke (1959), Greek text reedited with French translation by Allard (1980), Arabic text edited with English translation by Sesiano (1982), Arabic text reedited with French translation by Rashed (1984).
Conics, Apollonius: Greek text of Books I–IV edited with Latin translation by Heiberg (1891–1893), Arabic text of Books V–VII edited with English translation and commentary by Toomer (1990), Greek text of Books I–IV reedited with French translation by Decorps-Foulquier and Federspiel (2008–2010), Arabic text of Books I–VII edited with French translation and commentary by Rashed (2008–2010).
Cutting off a Ratio, Apollonius: Arabic text edited with French translation by Rashed and Bellosta (2010). English translation, directly from the Arabic manuscripts, by Macierowski and Schmidt (1987).
Data, Euclid: Greek text edited with Latin translation by Menge (1896), German translation by Thaer (1962), English translation by Mcdowell and Sololik (1993), Greek text reprinted with English translation and commentary by Taisbak (2003), Greek text reprinted with Italian translation by Acerbi (2007, 1860–2113).
Dioptra, Heron: Greek text edited with German translation by Schöne (1903, 188–315). English translation of much of the text by Lewis (2001, 259–286).Footnote 142
Elements (Elem.), Euclid: Greek text edited with Latin translation by Heiberg and Heiberg and Stamatis (1969–1977), English translation with commentary by Heath (1908), French translation and commentary by Vitrac (1990–2001), Greek text reprinted with Italian translation by Acerbi (2007, 778–1857).
Measurements (Meas.), Heron: Greek text edited with German translation by Schöne(1903, 2–185), Greek text reedited with French translation and commentary by Acerbi and Vitrac (2014)
Polygonal Numbers, Diophantus: Greek text edited with Latin translation by Tannery (1893–1895, 450–481), French translation by Ver Eecke (1959, 275–295), Greek text reedited with Italian translation and commentary by Acerbi (2011b).
Rights and permissions
About this article
Cite this article
Sidoli, N. The concept of given in Greek mathematics. Arch. Hist. Exact Sci. 72, 353–402 (2018). https://doi.org/10.1007/s00407-018-0211-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00407-018-0211-5





 that has both philosophical and mathematical implications. I do not see that this difference has, however, any meaning for the mathematical practice. Acerbi points out that, in the Data, finite verb forms are also used with what appears to be the same meaning, and he gives statistics for the occurrences of the various forms of the particle in canonical authors (Acerbi
that has both philosophical and mathematical implications. I do not see that this difference has, however, any meaning for the mathematical practice. Acerbi points out that, in the Data, finite verb forms are also used with what appears to be the same meaning, and he gives statistics for the occurrences of the various forms of the particle in canonical authors (Acerbi  ) in the hypothesis of the problem”—is the given are mistaken (Menge
) in the hypothesis of the problem”—is the given are mistaken (Menge  ) despite his later claim that
) despite his later claim that  ), because it is
), because it is  is a technical expression in Ptolemy’s writings (Heiberg
is a technical expression in Ptolemy’s writings (Heiberg  ), but this is the standard expression by ellipsis for given in position, often used in Euclid’s Data and probably in Apollonius’ Cutting off a Ratio. As just one example, see Data 43 , Sect.
), but this is the standard expression by ellipsis for given in position, often used in Euclid’s Data and probably in Apollonius’ Cutting off a Ratio. As just one example, see Data 43 , Sect. 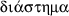 , the span with which a circle is drawn (Sidoli
, the span with which a circle is drawn (Sidoli 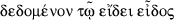 ). Data Def. 3 construes given in form as applying to rectilinear figures, and the proof of this proposition makes it clear that the “form” we are dealing with here is, in fact, a rectilinear figure.
). Data Def. 3 construes given in form as applying to rectilinear figures, and the proof of this proposition makes it clear that the “form” we are dealing with here is, in fact, a rectilinear figure. in relation to the concept of given. Federspiel (
in relation to the concept of given. Federspiel (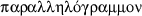 to mean rectangle. This is not uncommon in Greek mathematical texts. For example, Archimedes also employs the term in this way (Heiberg and Stamatis
to mean rectangle. This is not uncommon in Greek mathematical texts. For example, Archimedes also employs the term in this way (Heiberg and Stamatis  ) to refer to geometric objects that have “extent” (
) to refer to geometric objects that have “extent” ( ), in his actual works the meaning of the term is broader and refers also to angles, numbers, movements, and so on; and that whenever we read quantity we should also understand number (Lorch
), in his actual works the meaning of the term is broader and refers also to angles, numbers, movements, and so on; and that whenever we read quantity we should also understand number (Lorch 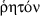 refers to what is precisely expressible in terms of some arbitrary measure, and hence relates to the distinction between what is commensurable and incommensurable—as, for example, in Elements X. Hence, the concept is mathematically related to our notion of a rational number, and the word is sometimes translated in this way. There is a long literature on this material that need not concern us here.
refers to what is precisely expressible in terms of some arbitrary measure, and hence relates to the distinction between what is commensurable and incommensurable—as, for example, in Elements X. Hence, the concept is mathematically related to our notion of a rational number, and the word is sometimes translated in this way. There is a long literature on this material that need not concern us here. is used by Apollonius, Conics II.44 to set out a line given in position, as seen above, Sect.
is used by Apollonius, Conics II.44 to set out a line given in position, as seen above, Sect.  is used as a synonym of given in Euclid’s Optics A 18 (Heiberg
is used as a synonym of given in Euclid’s Optics A 18 (Heiberg  in Dioptra 13, 14 and elsewhere to mean given (Schöne
in Dioptra 13, 14 and elsewhere to mean given (Schöne  by Apollonius in the enunciation and exposition of a number of theorems of the Conics is unrelated to the concept of given. The discussion by Acerbi (
by Apollonius in the enunciation and exposition of a number of theorems of the Conics is unrelated to the concept of given. The discussion by Acerbi (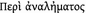 : An Annotated Transcription of Moebeke’s Latin Translation and of the Surviving Greek Fragments, with an English Version and Commentary. PhD Thesis, Department of Classics, Brown University.
: An Annotated Transcription of Moebeke’s Latin Translation and of the Surviving Greek Fragments, with an English Version and Commentary. PhD Thesis, Department of Classics, Brown University.