Abstract
Mei-yu fronts are often accompanied with prominent diabatic heating due to the development of frontal clouds and rain bands. The direct effect and relative importance of diabatic heating on the spatiotemporal morphology of Mei-yu fronts however remain unclear. Here a new frontogenesis function is derived to isolate the effect of diabatic heating and this function is then applied to the latest high resolution reanalysis product ERA5 to conduct an initial survey of dynamic and thermodynamic processes driving the intensity and structure evolutions of three typical Mei-yu fronts. It is found that the direct effect of latent heating (moisture depletion) is always frontogenetical (frontolytical) in the pre-frontal and frontal zone throughout the lifecycle of the front with latent heating (moisture depletion) in general dominates the front intensification (dissipation). Tilting is another critical process that turns the vertical gradient of equivalent potential temperature into horizontal gradient leading to frontogenesis during the front development stage, and, after the release of convective instability ahead of the front, flattens the front surface leading to frontolysis during the front decaying stage. Therefore titling maintains consistently positive contributions to the evolution of a Mei-yu front and its importance depends highly on the convective intensity near the front. The deformation effect appears frontogenetical but carries a much smaller weight compared to diabatic heating, moisture depletion and tilting. The structure evolutions of the three Mei-yu fronts studied here exhibit two distinct patterns: “bending and breaking”, and “moving and rotating”. Both patterns are dominated by the front propagation (i.e., frontogenesis through air parcels), further highlighting the critical roles played by diabatic heating, moisture depletion and titling in determining the spatiotemporal characteristics of Mei-yu fronts. As these three processes are all closely tied to updrafts, clouds and precipitation near the fronts, improved representations of clouds and convection are needed to accurately depict their feedbacks to frontal evolutions and ultimately achieve better predictions of heavy rainfall and floods associated with Mei-yu fronts.
Similar content being viewed by others
1 Introduction
The early- to mid-summer monsoon over East Asia is characterized by a quasi-stationary front known as the Mei-yu front (or Baiu front in Japan) typically extending from the middle and lower reaches of the Yangtze River basin to the southern Japan. On synoptic scales, the Mei-yu front develops and decays repeatedly, triggering the successive formation of frontal cloud bands and heavy rainfall during the Mei-yu season. The Mei-yu front and the associated rainfall have a profound socio-economic impact on the densely populated Yangtze River basin. The typical Mei-yu front or the western section of the Mei-yu and Baiu frontal system is characterized by weak baroclinicity, pronounced moisture contrast, an equivalent barotropic structure, and strong cyclonic wind shear at low-levels (Chen and Chang 1980; Ninomiya 1984; Ding 1992; Cui et al. 2019). These suggest that Mei-yu fronts differ substantially from classic polar/mid-latitude fronts featuring strong horizontal temperature gradients and vertical tilts.
Similar to polar and mid-latitude fronts, Mei-yu fronts are associated with strong diabatic heating due to the formation of frontal clouds and heavy rainfall that may provide effective feedbacks to the frontal circulation. For example, there have been extensive modeling studies using different microphysical and convective heating parameterizations to evaluate the effect of diabatic heating on mid-latitude fronts/cyclones (e.g., Mak and Bannon 1984; Thorpe and Emanuel 1985; Huang and Emanuel 1991; Lagouvardos et al. 1993; Parker and Thorpe 1995; Forbes and Clark 2003; Dearden et al. 2016; Lin et al. 2018). Among the findings are that diabatic heating could lead to local frontogenesis/cyclogenesis, enhanced frontal updraft/downdraft and narrowed horizontal scale of frontal circulations. Modeling analyses on selected cases of Mei-yu fronts also highlighted a positive feedback mechanism similar to the conditional instability of the second kind (CISK) where Mei-yu fronts organize the convection and condensation heating further intensifies Mei-yu frontal circulations (Cho and Chen 1995; Chen et al. 1998).
The dynamic impact of diabatic heating on frontal circulations is typically understood within the potential vorticity (PV) framework, as diabatic heating can produce a dipole of PV anomaly in the vertical direction (i.e., PV is increased below a region of the maximum heating source and decreased above; see Hoskins et al. 1985; Hoskins 1997). In the vicinity of a mid-latitude frontal-cyclone system, various diabatic heating processes along the slantwise updraft/downdraft could produce multiple dipoles of PV anomalies generating an overall complex pattern of PV production (e.g., Joos and Wernli 2012; Crezee et al. 2017; Attinger et al. 2019). Joos and Forbes (2016) showed that diabatic PV modification may influence the location of upper-level warm conveyor belt outflow and even the PV pattern far downstream of a mid-latitude frontal-cyclone system. The rate of diabatic PV modification is proportional to the magnitude of existing absolute vorticity. Therefore, even in a Mei-yu front background bearing little baroclinic forcing (i.e., ageostrophic response to thermal wind imbalance), the condensation heating effect may still be pronounced and efficient due to the strong vorticity associated with Mei-yu fronts. Additionally, the CISK-like interaction between low-level PV and convective heating is highly nonlinear and intensifies the Mei-yu front rapidly (Cho and Chen 1995). Chen et al. (2003, 2006, 2008) thus concluded that convective heating is the major contributor to the Mei-yu frontogenesis, the growth of wavelike frontal disturbances and the formation/intensification of low-level jet ahead of Mei-yu front. Zhang and Tan (2009) also suggested the key role of similar feedback processes in enhancing the Mei-yu frontal circulation and interactions among weather systems of multiple scales.
Despite all the efforts investigating the feedback of diabatic heating to frontal circulations, the direct effect of heating on frontogenesis has received limited attention so far and appears to be complex and controversial in moist front cases. Based on horizontal/vertical frontogenesis functions, Igel and van den Heever (2014) indicated that the primary impact of latent heating on a warm front is to weaken the front by decreasing the front slope even though the heating contributes to horizontal frontogenesis. Mak et al. (2017) found that the diabatic heating processes are comparably important as dry dynamical processes in surface frontogenesis of an extratropical cyclone and also contribute to the narrowing of cold fronts. In a Mei-yu front case, Chen et al. (2007) found that diabatic heating is frontogenetical during the formation stage but strongly frontolytical during the intensification stage with the front being maintained through the deformation and convergence effect. However, the findings of Chen et al. (2007) may be of limited applicability to typical Mei-yu fronts as the front considered there evolved into a strong baroclinic system under the influence of a blocking high at mid-high latitudes and was defined by potential temperature gradient similar to a mid-latitude front. Ninomiya (1984) put forward the Mei-yu/Baiu front frontogenesis function using equivalent potential temperature \(\left({\theta }_{e}\right)\) gradient to define the front intensity and it was shown that deformation is the predominant frontogenesis term. The importance of deformation flow was highlighted later by more studies where the large-scale flow associated with Mei-yu fronts were found to exhibit a deformation pattern favoring frontogenesis (Zhou et al. 2004; Gao et al. 2008; Yang et al. 2014; Yang et al. 2015).
Since total diabatic heating was considered in earlier studies (e.g., Ninomiya 1984; Zhou et al. 2004), the effect of latent heating alone has yet to be explicitly evaluated in terms of a classic Mei-yu frontogenesis function. The most recent work on the development of Mei-yu fronts and Mei-yu rainfall also tend to focus on dry dynamical processes (e.g., Gao et al. 2008; Yang et al. 2014, 2015). Therefore, it remains unclear how diabatic heating, especially latent heating, contributes to the spatiotemporal morphology of Mei-yu front throughout its lifecycle and what is the relative importance of diabatic heating compared to other dynamical and thermodynamical processes in determining the evolution of a Mei-yu front. To address these questions, we derive a new frontogenesis function to isolate the effect of diabatic heating (including latent heating) from the rest terms and also quantify with new metrics the contributions of different processes to the spatiotemporal morphology of typical Mei-yu fronts. The remaining part of this paper is organized as follows. Section 2 describes the data used and introduces the new frontogenesis function. Section 3 applies the new function to quantify and elucidate the contributions of multiple processes to the intensity and structural evolutions of selected typical Mei-yu fronts. A summary is given in Sect. 4.
2 Data and methodology
2.1 Data
Two sources of data were used in our study. The rainfall data is extracted from a gauge-satellite merged precipitation dataset developed by the China Meteorological Information Center (Shen et al. 2014). This gridded (0.1° × 0.1°) data merged the rain gauge data at more than 30,000 automatic weather stations in China and the Climate Prediction Center Morphing precipitation product. The atmospheric fields diagnosed are from the fifth generation of the European Centre for Medium-Range Weather Forecasts Reanalysis (ERA5), with an hourly time interval, a horizontal resolution of 0.25° × 0.25° (Copernicus Climate Change Service 2017). The variables used in our analysis include temperature, specific humidity, relative vorticity, horizontal and vertical wind velocity on 37 isobaric levels.
2.2 Definition of the Mei‐yu front
As the Mei-yu front is often characterized by a weak temperature gradient and strong moisture contrast at low-levels (Chen and Chang 1980; Ninomiya 1984; Cui et al. 2019), the Mei-yu front intensity is represented by the horizontal gradient of equivalent potential temperature (\(\left|\nabla {\theta }_{e}\right|\)) at 800 hPa in our study. In the analysis that follows, the Mei-yu frontal zone is defined as the region where the front intensity exceeds 10 K 100 km− 1 (\(\left|\nabla {\theta }_{e}\right|\) ≥ 10 K 100 km− 1) over continuous grids. \({\theta }_{e}\) is calculated following Eq. (35) of Bolton (1980) as
where \(\theta\) is the potential temperature (units: K); r is the mixing ratio (kg kg− 1). And TL is the temperature (units: K) at the lifting condensation level that can be obtained from the temperature, pressure and mixing ratio (see Eq. (21) in Bolton 1980).
2.3 Spatiotemporal morphology of the Mei‐yu front: intensity and structure evolution
The Mei-yu frontogenesis, defined as the total derivative of \(\left|\nabla {\theta }_{e}\right|\) with respect to time, is used to represent the evolution of the Mei-yu front intensity. To evaluate the contributions of various processes including latent heating to the Mei-yu frontogenesis, we expanded the diabatic term in the traditional frontogenesis function (Ninomiya 1984) using Eq. (1). The new frontogenesis function is
where the forcing terms (i.e., FGn) on the right-hand side include
Here ω is the vertical velocity in p-coordinates and the rest of the symbols and annotations are otherwise standard. FG1a is the new diabatic heating term containing all the heating/cooling effects from the phase changes of water substances, radiation and turbulent mixing. FG1b represents the effect of moisture changes. FG1c is associated with changes in lifting condensation temperature (TL), which was found negligible in our analysis. FG2, FG3 and FG4 are the convergence, deformation and tilting terms respectively as in the traditional frontogenesis function. The total derivative is computed following Eq. (9) as,
Centered finite differencing is used to approximate all the partial derivatives in Eqs. (2)–(9). The local derivative \(\left(\partial / \partial t \right)\) in Eq. (9) is evaluated at a higher temporal resolution of 10-min using the cubic spline fitting, which has been shown to effectively reduce the residual between F and the sum of its forcing terms (Chen et al. 2007).
The structure and shape of a Mei-yu front are influenced by the local front movement, which are related to the distribution of the local derivative of the front intensity (Chen et al. 2007; Wang et al. 2016; Mak et al. 2017). For instance, when the local derivative \({{\partial \left| {\nabla \theta _{e} } \right|} \mathord{\left/ {\vphantom {{\partial \left| {\nabla \theta _{e} } \right|} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}\) peaks ahead of (behind) a Mei-yu front, the local front tends to move forward (backward). The relative importance of factors contributing to a Mei-yu front’s structure evolution can be quantified by decomposing the local derivative \({{\partial \left| {\nabla \theta _{e} } \right|} \mathord{\left/ {\vphantom {{\partial \left| {\nabla \theta _{e} } \right|} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}\) into three components via rearranging Eq. (9): (1) the total derivative F \(\left(\frac{d\left|\nabla {\theta }_{e}\right|}{dt} \right)\), which is the front propagation (frontogenesis) following the movement of air parcels, (2) the horizontal advection term \(\left( -u\frac{\partial \left|\nabla {\theta }_{e}\right|}{\partial x}-v\frac{\partial \left|\nabla {\theta }_{e}\right|}{\partial y} \right)\) and (3) the vertical advection term \(\left( -\omega \frac{\partial \left|\nabla {\theta }_{e}\right|}{\partial p} \right)\). The two advection terms can be interpreted as the front transport by air parcels (Chen et al. 2007; Wang et al. 2016).
The projection coefficients (e.g., Jiang and Deng 2011) are used to quantify the contributions to a specific spatial pattern by individual components. For instance, the projection coefficient onto F by each forcing term (FGn) is expressed as
where \((j,i)\) indicates all grid points in the study domain. \(\left|\nabla {\theta }_{e}(j,i)\right|\) is used to assign greater weights to grid points closer to the frontal zone to focus on the spatiotemporal morphology of Mei-yu fronts.
3 Results
3.1 Overview of three representative cases of Mei‐yu fronts
We selected three cases of Mei-yu fronts that occurred on 2 July 2016 (Case 1), 19 June 2010 (Case 2) and 8 July 2010 (Case 3). These cases are selected and considered to be representative of Mei-yu fronts since (1) they share classic features of Mei-yu fronts (i.e., weak baroclinicity, large gradient of \({\theta }_{e}\)); (2) all of them triggered extreme rainfall and severe flooding over the middle and lower reaches of the Yangtze River basin and resulted in substantial economic losses and casualties; and (3) the three cases also bear differences (i.e., front intensity, front structure) that are representative of the diversity of typical high impact Mei-yu fronts.
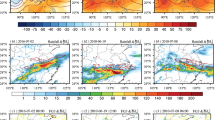
The daily rainfall and front intensity at 800 hPa are shown in Fig. 1 for all three cases. The close relationship between rainfall and fronts is evident as the rainbelt is located just ahead of the Mei-yu front and nearly parallel with the front in all three cases. Also slightly ahead of the front is the zone of maximum relative vorticity that always coincides with the Mei-yu front (Fig. 1). This vorticity maxima drives moisture convergence and rising motion, and provides the background vorticity for the nonlinear-CISK mechanism of front development (Chen and Chang 1980; Chen et al. 2006; Wang et al. 2016). All the three Mei-yu fronts have a semi-zonal orientation and are located at slightly different latitudes. The meridional ranges of the three cases are 31–33° N, 28.5–30.5° N and 29–32.5° N respectively. The front intensity is averaged along these latitude ranges and a time-longitude Hovmöller diagram of the averaged intensity is used to depict the evolution of the frontal zone in Fig. 2. The mature stage of the front is generally marked by a zonally elongated region of maximum \(\left|\nabla {\theta }_{e}\right|\) accompanied with a zone of strong relative vorticity. According to these features and the hourly \(\left|\nabla {\theta }_{e}\right|\) map (figures not shown), the mature time (labeled as t = 0 in Fig. 2) of the front is found to be 08:00 UTC 2 July 2016 in Case1, 12:00 UTC 19 June 2010 in Case 2, and 06:00 UTC 8 July 2010 in Case 3. The lifecycle of the front is generally completed between t = − 10 and t = 10 in Fig. 2 for each case. Based on Figs. 1 and 2, the study domains for the three typical Mei-yu fronts are selected as (31–33° N, 114–120° E), (28.5–30.5° N, 109–117° E) and (29–32.5° N, 116–122° E) respectively (see brown boxes in Figs. 8, 9, 10). In the following analysis, the study-domain averages and the projection coefficients are calculated based on all the grid points in the study domain, while the frontal mean are averaged over the frontal zone (\(\left|\nabla {\theta }_{e}\right|\) ≥ 10 K 100 km− 1) within the study domain.
Time-longitude Hovmöller diagram of front intensity (\(\left|\nabla {\theta }_{e}\right|\); color shading; units: K 100 km− 1) and relative vorticity (dotted; ≥ 5 × 10− 5 s− 1) at 800 hPa from 20 h before (t = − 20) and 20 h after (t = 20) the front mature time (t = 0 in Y-axis) in a Case 1, b Case 2 and c Case 3
Mean frontogenesis (F; solid lines; units: 10− 9 K m− 1 s− 1) and the sum of all contributory terms (FGn-Sum; dashed lines) over the frontal zone (\(\left|\nabla {\theta }_{e}\right|\) ≥ 10 K 100 km− 1) at 800 hPa from 10 h before (t = − 10) and 10 h after (t = 10) the front mature time (t = 0 in X-axis) in Case 1 (red lines; 31–33° N, 114–120° E), Case 2 (blue lines; 28.5–30.5° N, 109–117° E) and Case 3 (green lines; 29–32.5° N, 116–122° E)
a Mean frontogenesis (F; black dashed lines) and each contributory term (FGn; colored dashed lines) at 800 hPa over the frontal zone (left axis; units: 10− 9 K m− 1 s− 1) and b the projection coefficients (left axis) onto F by each FGn term and the sum of projection coefficients of all FGn terms (FGn-Sum; grey solid lines) over the study domain in Case 1 (left column), Case 2 (middle column) and Case 3 (right panel). The histogram represents the a frontal mean and b study-domain mean front intensity (\(\left|\nabla {\theta }_{e}\right|\); right axis; units: K 100 km− 1). The X-axis indicates the time (units: h) relative to the front mature time
The cross-sections of equivalent potential temperature (\({\theta }_{e}\); grey contours; units: K) and a frontogenesis (F; color shading; units: 10− 9 K m− 1 s− 1), b diabatic heating term (FG1a; color shading) and diabatic heating rate (blue contours; K day− 1) and c moisture change term (FG1b; color shading) at 04:00 UTC 2 July 2016 (Case 1) averaged along (116–118° E). The green dots indicate the frontal zone (\(\left|\nabla {\theta }_{e}\right|\) ≥ 10 K 100 km− 1)
Figure 3 shows the total frontogenesis F (solid lines) evaluated using the observed front intensity in the frontal zone as a function of time and the sum of FGn terms according to Eq. (2) (dashed lines). The small differences between the direct estimate and the sum of forcing terms on the right-hand side of Eq. (2) suggest that the frontogenesis function derived in our analysis successfully captures the actual evolution of the front intensity. Besides the consistency in averages over the frontal zone, the spatial pattern of F and the sum of FGn terms are also quite close over the study domain as the sum of the projection coefficients of FGn terms is close to 1 in general (grey solid lines in Fig. 4b). The developing (decaying) stage of the Mei-yu front is roughly from t = − 10 to t = 0 (t = 0 to t = 10) in Case 1 and Case 2, and from t = − 5 to t = 0 (t = 0 to t = 5) in Case 3. As it should be, F is positive with a large magnitude during the front developing stage. During the decaying stage, the mean front intensity over the frontal zone/study domain (grey histograms in Fig. 4) decreases with F being weakly negative or positive.
The cross-sections of equivalent potential temperature (\({\theta }_{e}\); grey contours; units: K), tilting term (FG4; color shading) and meridional circulation (units of the vertical and meridional velocity are 10− 1 Pa s− 1 and m s− 1 respectively) at a 04:00 UTC and b 09:00 UTC on 2 July 2016 (Case 1) averaged along (116–118° E). The green dots indicate the frontal zone (\(\left|\nabla {\theta }_{e}\right|\) ≥ 10 K 100 km− 1)
Same as Fig. 6 but at a 07:00 UTC and b 19:00 UTC on 19 June 2010 (Case 2) and averaged along 110–112° E and 115–117° E respectively
3.2 Mei‐yu frontogenesis and frontolysis
3.2.1 Contributions from individual forcing terms
The frontal mean values of each FGn term and their projection coefficients onto F in the study domain are shown in Fig. 4a and b respectively to illustrate individual dynamical and thermodynamical processes’ contributions to the Mei-yu frontogenesis throughout its lifecycle. As shown in Fig. 4a, the diabatic heating term (FG1a) is always positive and thus frontogenetical, while the moisture change term (FG1b) is always frontolytical within the entire Mei-yu front lifecycle. In the frontal zone, these two terms in general represent the frontogenesis and frontolysis term of the largest magnitude, respectively. The tilting term (FG4) remains a positive contribution to the evolution of the front throughout its lifecycle, i.e., being frontogenetical as the front develops and frontolytical as the front decays. During the developing stage, the magnitude of FG4 can be comparable to FG1a and even higher than FG1a in Case 3 where the front decays before FG1a reaches its peak. Although FG4 only has small negative values in the decaying stage, FG4 and FG1b are the only two terms contributing to frontolysis. FG3 (deformation term) is a distinct frontogenesis term as expected from classic dry front theory, but its magnitude is generally smaller than those of FG1a and FG4 in our three Mei-yu front cases. FG2 (convergence) and FG1c (TL variation term) are negligible in the frontal zone due to their small magnitudes.
The relative contribution of each forcing term to the Mei-yu frontogenesis pattern in the study domain shown in Fig. 4b is consistent with the frontal averages given in Fig. 4a. Specifically, FG1a (diabatic heating) nearly dominates the front development (except for being the second dominant term in Case 3), while FG1b (moisture change) dominates the front dissipation. FG4 (tilting) is an important positive contributor to F throughout the entire lifecycle of fronts. It is the most dominant (Case 3) or second most dominant (Case 2) contributor during the front developing stage; it is always the second most dominant term in the decaying stage except for being weak and fluctuating in Case 1. Similar to the results of frontal averages, FG3 (deformation) is the third (Case 2 and Case 3) or second (Case 1) important contributor to frontogenesis during the development stage. But the projection coefficients of FG3 onto F are generally small except in Case 1. Unlike the negligible frontal average values due to the cancellation of positive and negative values within the frontal zone, FG2 (convergence) has a weak but discernable frontogenesis contribution over the study domain with the projection coefficient ranging from 0.1 to 0.3. This is caused by the fact that FG2 bears a spatial pattern similar to that of F (figures not shown). FG1c’s contribution to F is negligible both in terms of average over the frontal zone and spatial projection over the study domain.
3.2.2 Forcing mechanisms: diabatic heating versus other dynamical processes
The cross-frontal structure passing through the center of the front (116–118° E) in Case 1 is shown in Figs. 5 and 6. These figures illustrate the structures of diabatic heating (FG1a; \(d\theta /dt\)), moisture change (FG1b; \(dr/dt\)) and tilting (FG4), the three most important frontogenesis and frontolysis terms. Note that we mainly focus on the effects of these forcing terms on the 800 hPa Mei-yu front, which captures the general features of Mei-yu fronts at low-levels from 750 to 850 hPa.
The actual front structure (represented by the map of \(\left|\nabla {\theta }_{e}\right|\); black contours; units: K) at 800 hPa and the reconstructed front structure (color shading) with a only frontogenesis (F; left column) and b only horizontal advection of front intensity (right column) from 5 h before (t = − 5) to 5 h after (t = 5) the front mature time in Case 1. The brown box indicates the study domain
Same as Fig. 8 but for Case 2
As shown in Fig. 5b, strong diabatic heating (\(d\theta /dt>0\)) associated with updraft (Fig. 6a) and latent heating is found ahead of the Mei-yu front (about 31–31.5° N) and along the front surface throughout the mid-low troposphere. According to Eq. (3), FG1a is determined by the projection of the gradient of diabatic heating onto the gradient of equivalent potential temperature \(\nabla {\theta }_{e}\). \(\nabla {\theta }_{e}\) generally points to the south (perpendicular to the Mei-yu front) in the vicinity of the Mei-yu front, while the strong heating gradient pointing to the south is found north of the heating center. Therefore, diabatic heating produces a distinct and vertically deep region of frontogenesis near the frontal zone to the north of the heating center. Note that FG1a also leads to a vertically shallower region of weaker frontogenesis south of the heating center in the pre-frontal region (around 31° N), where the gradients of \({\theta }_{e}\) and diabatic heating both point to the north. Note that the local \({\theta }_{e}\) perturbation leading to the reversed direction of \(\nabla {\theta }_{e}\) at mid-low levels also results from the strong diabatic heating in the updraft. Therefore, diabatic (latent) heating generally leads to strong frontogenesis in the pre-frontal and frontal zone. Again, while the maximum frontogenesis due to diabatic heating is found at mid-levels around 500–600 hPa, we focus on the contribution of FG1a at low-levels (around 800 hPa) where a Mei-yu front is typically defined. The same mechanism applies to the moisture change term (FG1b). As the moisture is depleted (\(dr/dt<0\)) in the updraft, FG1b tends to cause frontolysis in the pre-frontal and frontal region. The processes discussed above are active throughout the lifecycle of the Mei-yu front in Case 1 and are also clearly present in other two cases (figures not shown).
The titling effect (FG4) is associated with the horizontal variations of vertical motion according to Eq. (8) and is also dominated by the meridional component (i.e., \(-\frac{1}{\left|\nabla {\theta }_{e}\right|}\frac{\partial {\theta }_{e}}{\partial p} \frac{\partial {\theta }_{e}}{\partial y}\frac{\partial \omega }{\partial y}\)). As shown in Fig. 6, the developing stage (Fig. 6a) features strong pre-frontal updraft and weak post-frontal downdraft while the decaying stage (Fig. 6b) is characterized by weaker updraft and enhanced downdraft, producing a constant, north-pointing ω gradient (\(\partial \omega /\partial y>0\)). \(\partial {\theta }_{e}/\partial y\) is generally negative in the frontal zone (i.e., south-pointing \({\theta }_{e}\) gradient) leading to negative values of \(\frac{\partial {\theta }_{e}}{\partial y}\frac{\partial \omega }{\partial y}\). Therefore, whether FG4 is frontogenetical or frontolytical is determined by convective instability properties of the environment (\(-\partial {\theta }_{e}/\partial p\)). During the front intensification stage, the environment is convectively unstable (\(-\partial {\theta }_{e}/\partial p<0\)) around the Mei-yu front (31.5–32° N) at low-levels from 750 to 850 hPa (Fig. 6a), which may be associated with the differential advection of \({\theta }_{e}\) (Ninomiya and Akiyama 1992). Therefore, FG4 is frontogenetical in the intensification stage. However, as the convective instability is released in the mature and weakening stages, the frontal zone becomes convectively stable (\(-\partial {\theta }_{e}/\partial p>0\)) and FG4 turns frontolytical (Fig. 6b). Another straightforward way to interpret it: the thermally direct cross-frontal circulation in both stages tends to turn the front surface clockwise in the cross-front transection. In the front developing stage, the Mei-yu front surface tilts southward. Thus the titling effect tends to turn the vertical component of \({\theta }_{e}\) gradient (\(\left|\partial {\theta }_{e}/\partial p\right|\)) into horizontal component (\(\left|\partial {\theta }_{e}/\partial y\right|\)), leading to horizontal frontogenesis (Fig. 6a). However, the front surface tilts northward in the decaying stage and tilting tends to flatten the front surface further and cause frontolysis (Fig. 6b).
FG4’s consistently positive contribution to the Mei-yu front evolution is more evident in Case 2 and Case 3, as quantified in terms of averages over the frontal zone and projections over the study domain (Fig. 4). The cross-front section of Case 2 is shown in Fig. 7 as an example to illustrate why FG4 is more effective in Case 2. The main characteristics identified above in Case 1 is clearly present in Case 2, but Case 2 shows a more prominent convective structure: (1) stronger updraft ahead of the front in both the developing and decaying stages leading to enhanced meridional ω gradient (i.e., higher tilting potential); and (2) higher convective instability in the developing stage (i.e., more southward tilting front surface). Therefore the presence of stronger convective features and cross-frontal circulation is responsible for the more pronounced effect of titling in Case 2. The same idea applies to Case 3 (figures not shown).
Same as Fig. 8 but for Case 3
3.3 Structure evolutions of the Mei‐yu fronts
Figures 8, 9 and 10 show the structure evolutions of the three Mei-yu front cases (black contours) from 5 h before (t = − 5) to 5 h after (t = 5) the front mature time. The evolutions can be classified into two distinct types. We characterize the structure change of the front in Case 1 as being “bending and breaking”: the central part of the front moves southward until the mature stage and then the front breaks into two parts with the west (east) part taking a northwest (northeast) orientation and moving slightly toward the northwest (northeast) after the breaking. The structure evolution in Case 2 (Fig. 9) and Case 3 (Fig. 10) are best described as being “moving and rotating”. In Case 2 (Case 3), the front moves eastward (northeastward) and rotates anticlockwise from a zonal (northwest) to a northeast (west–northwest) orientation.
As discussed in Sect. 2.3, the structure/shape evolution of the Mei-yu front is determined by the local derivative of front intensity (\(\partial \left|\nabla {\theta }_{e}\right|/\partial t\)). A comparison of the three components of the local derivative indicates that \(\partial \left|\nabla {\theta }_{e}\right|/\partial t\) is dominated by frontogenesis (F) and the horizontal advection of front intensity (H-ADV) while the magnitude of the vertical advection term is negligible (figure not shown). The relative importance of F and H-ADV in determining the structure evolution of the front is further evaluated by reconstructing the front evolution with only F (color shading, left panels in Figs. 8, 9, 10), and with only H-ADV (color shading, right panels in Figs. 8, 9, 10). It is seen from Fig. 8a that the “bending and breaking” feature is in general captured by the reconstruction using F except for a relatively large deviation at t = 5 likely due to the accumulation of computational errors. On the contrary, the reconstruction with only H-ADV (Fig. 8b) only resembles the actual front at the beginning (t = − 5). Therefore, the structure evolution of the Mei-yu front appears to be dominated by F in Case 1. Similar results are obtained for the two “moving and rotating” cases (Figs. 9, 10), suggesting that processes of frontogenesis dictate the structure evolution of Mei-yu fronts.
This conclusion is further verified by Fig. 11, which shows the projection coefficients of H-ADV, F and the essential components of F (i.e., FG1a, FG1b, FG4 and FG3) onto \(\partial \left|\nabla {\theta }_{e}\right|/\partial t\) throughout the lifecycle of the front. In all three cases, H-ADV only dominates the evolution of the front structure in a relatively short period around the mature and early developing stage when F is weak. Frontogenesis (F) dictates the overall structure evolution of the front during the developing and decaying stages. Among the individual frontogenesis terms (FGn), diabatic heating (FG1a) and tilting (FG4) represent the two most important processes for the structure evolution in the front developing stage; moisture depletion (FG1b) and tilting (FG4) are more critical for the structure evolution in the front decaying stage. In summary, the front propagation (F) dominates the structure evolution of Mei-yu fronts in the front developing and decaying stages, whereas the front transport by horizontal flow plays a more important role during the mature and early developing stages.
The projection coefficients (left axis) onto local derivative of front intensity (\(\partial \left|\nabla {\theta }_{e}\right|/\partial t\)) by total frontogenesis (F; black solid lines), individual frontogenesis contributory terms (FGn; colored lines) and the horizontal advection of front intensity (H-ADV; dashed orange lines) at 800 hPa in a Case 1, b Case 2 and c Case 3. The histogram represents the average front intensity (\(\left|\nabla {\theta }_{e}\right|\); right axis; units: K 100 km− 1) in the study domain. The X-axis indicates the time (units: h) relative to the front mature time
4 Summary
In this study, we derived a new frontogenesis function that isolates the diabatic heating effect from the rest of the forcing terms. The new function was used to conduct an initial survey of dynamical and thermodynamical processes dictating the intensity and structure evolutions, thus the spatiotemporal morphology of three typical Mei-yu fronts associated with heavy rainfall over the central-eastern China. The typical Mei-yu fronts are representative of moist fronts characterized by weak baroclinity, strong moisture contrast and horizontal wind shear. This kind of moist fronts may occur slightly before or after a Mei-yu season (Luo et al. 2013) and thus may share similar results to those presented here.
It is found that the direct effect of diabatic heating (FG1a) is always frontogenetical in the pre-frontal and frontal zone throughout the entire lifecycle of Mei-yu fronts and represents in general the most dominant forcing term during the front intensification stage. This persistent frontogenesis effect is associated with the positive projection of the latent heating gradient onto the gradient of equivalent potential temperature with the former largely induced by strong updrafts ahead of the front. On the contrary, moisture is depleted in ascending air. Thus the moisture depletion effect (FG1b) always acts to destroy the front and dominates the front decaying stage.
The tilting term (FG4) is in general the second important frontogenesis (frontolysis) term during the front developing (decaying) stage, and therefore makes consistent, positive contributions to the front evolution. During the front developing stage, the environment is convectively unstable (\(-\partial {\theta }_{e}/\partial p<0\)) around the frontal zone and the front surface tilts southward. The titling associated with differential vertical motion tends to turn the vertical component of \({\theta }_{e}\) gradient into horizontal component, leading to horizontal frontogenesis. As the convective instability is released in the mature and decaying stage, the front surface tilts northward and the cross-frontal circulation tends to flatten the front surface further leading to frontolysis. In situations with high convective intensity, the tilting effect could replace diabatic heating and become the most important frontogenesis process. Specifically, stronger convective features are associated with stronger tilting effects including higher tilting potential and more tilted front surface, which tend to speed up the entire evolution of Mei-yu fronts. The reversed titling effect on frontogenesis among different stages are unique in Mei-yu fronts. In contrast, the titling effect on polar fronts is consistently frontolytical (Igel and van den Heever 2014) as the front surface tilts poleward with height throughout its lifecycle.
The deformation term also intensifies the Mei-yu front in the developing stage as shown by previous studies (Ninomiya 1984; Zhou et al. 2004; Gao et al. 2008; Yang et al. 2014, 2015). However, the deformation frontogenesis is in general less important compared to effects of diabatic heating and titling as demonstrated here. This difference is due to the explicit consideration of latent heating in our new frontogenesis function. As discussed before, latent heating effect is not revealed by the diabatic term (\(d{\theta }_{e}/dt\)) of the traditional Mei-yu frontogenesis function (Ninomiya 1984; Zhou et al. 2004). The functions of Gao et al. (2008) and Yang et al. (2014, 2015) are built mainly from a dynamic viewpoint (i.e., emphasizing the effect of flow on the moist front). Additionally, the strength of the tilting effect is sensitive to the convective instability property of the environment, whose variations may not be captured well by data of relatively lower spatiotemporal resolutions. Given these, our results complement the existing literature on moist Mei-yu frontogenesis. Also note that our study focuses on the front development/decay associated with individual heavy rainfall events during the Mei-yu season, and therefore conclusions drawn here might not be applicable to the initial development of Mei-yu fronts at the beginning of the monsoon transition period when large-scale dynamics may play a more important role in the genesis of the fronts.
Although the three Mei-yu fronts studied here exhibit distinct patterns of structure evolutions (“bending and breaking” versus “moving and rotating”), the relative contributions to the structure evolution by individual terms are similar. Specifically, the front transport by horizontal flows dominates a front’s structure evolution only during the mature and the early developing stages while the front propagation (frontogenesis following the movement of air parcels) dictates the structure evolution most of the time within the front’s lifecycle. The individual frontogenesis terms (FGn) are found to make similar relative contributions to both the intensity and structure evolutions of a front, suggesting the overall importance of diabatic heating, moisture depletion and tilting in determining the spatiotemporal morphology of a typical Mei-yu front.
As diabatic heating, moisture depletion and titling effects are all closely tied to updrafts and associated cloud micro/macro-physics, misrepresentations of clouds and convection in weather and climate models inevitably lead to errors in the simulation and prediction of the spatiotemporal morphology of Mei-yu fronts. These errors in representing the behavior of Mei-yu fronts directly translate into biases in local rainfall prediction thus undermines our capability to prepare for heavy rainfall and floods during the monsoon season. Ongoing efforts to address this issue include field campaigns designed to better observe cloud micro/macro structures during Mei-yu season and modeling analyses using in-situ and remote sensing observations to constrain model parameters to enhance our skill of predicting hydrological hazards associated with Mei-yu fronts.
References
Attinger R, Spreitzer E, Boettcher M, Forbes R, Wernli H, Joos H (2019) Quantifying the role of individual diabatic processes for the formation of PV anomalies in a North Pacific cyclone. Q J R Meteorol Soc 145:2454–2476. https://doi.org/10.1002/qj.3573
Bolton D (1980) The computation of equivalent potential temperature. Mon Weather Rev 108:1046–1053
Chen GTJ, Chang CP (1980) The structure and vorticity budget of an early summer monsoon trough (Mei-Yu) over southeastern China and Japan. Mon Weather Rev 108:942–953
Chen SJ, Kuo YH, Wang W, Tao ZY, Cui B (1998) A modeling case study of heavy rainstorm along the Mei-Yu front. Mon Weather Rev 126:2330–2351. https://doi.org/10.1175/1520-0493(1998)126<2330:AMCSOH>2.0.CO;2
Chen GTJ, Wang CC, Liu S (2003) Potential vorticity diagnostics of a Mei-yu front case. Mon Weather Rev 131(11):2680–696. https://doi.org/10.1175/1520-0493(2003)131<2680:PVDOAM>2.0.CO;2
Chen GTJ, Wang CC, Lin LF (2006) A diagnostic study of a retreating Mei-Yu front and the accompanying low-level jet formation and intensification. Mon Weather Rev 134(3):874–896. https://doi.org/10.1175/MWR3099.1
Chen GTJ, Wang CC, Wang AH (2007) A case study of subtropical frontogenesis during a blocking event. Mon Weather Rev 135(7):2588–2609. https://doi.org/10.1175/MWR3412.1
Chen GTJ, Wang CC, Chang SW (2008) A diagnostic case study of Mei-yu frontogenesis and development of wavelike frontal disturbances in the subtropical environment. Mon Weather Rev 136(1):41–61. https://doi.org/10.1175/2007MWR1966.1
Cho HR, Chen GTJ (1995) Mei-Yu frontogenesis. J Atmos Sci 52(11):2109–2120
Copernicus Climate Change Service (C3S) (2017) ERA5: fifth generation of ECMWF atmospheric reanalyses of the global climate. Copernicus Climate Change Service Climate Data Store (CDS), date of access. https://cds.climate.copernicus.eu/cdsapp#!/home
Crezee B, Joos H, Wernli H (2017) The microphysical building blocks of low-level potential vorticity anomalies in an idealized extratropical cyclone. J Atmos Sci 74(5):1403–1416. https://doi.org/10.1175/JAS-D-16-0260.1
Cui CG, Hu BW, Wang XF, Li SS, Zhou W (2019) Research progress on the equivalent-barotropic shear type Meiyu front heavy rain. Torrential Rain Disasters 38(5):541–553
Dearden C, Vaughan G, Tsai T, Chen JP (2016) Exploring the diabatic role of ice microphysical processes in two north atlantic summer cyclones. Mon Weather Rev 144(4):1249–1272. https://doi.org/10.1175/MWR-D-15-0253.1
Ding YH (1992) Summer monsoon rainfalls in China. J Meteorol Soc Jpn 70:373–396
Forbes RM, Clark PA (2003) Sensitivity of extratropical cyclone mesoscale structure to the parametrization of ice microphysical processes. Q J R Meteorol Soc 129(589):1123–1148. https://doi.org/10.1256/qj.01.171
Gao ST, Yang S, Xue M, Cui CG (2008) Total deformation and its role in heavy precipitation events associated with deformation-dominant flow patterns. Adv Atmos Sci 25(1):11–23. https://doi.org/10.1007/s00376-008-0011-y
Hoskins B (1997) A potential vorticity view of synoptic development. Meteorol Appl 4(4):325–334
Hoskins B, McIntyre ME, Robertson AW (1985) On the use and significance of isentropic potential vorticity maps. Q J R Meteorol Soc 111(466):877–946
Huang HC, Emanuel KA (1991) The effects of evaporation on frontal circulations. J Atmos Sci 48(4):619–628
Igel AL, van den Heever SC (2014) The role of latent heating in warm frontogenesis. Q J R Meteorol Soc 140:139–150. https://doi.org/10.1002/qj.2118
Jiang T, Deng Y (2011) Downstream modulation of North Pacific atmospheric river activity by East Asian cold surges. Geophys Res Lett 38:L20807. https://doi.org/10.1029/2011GL049462
Joos H, Forbes RM (2016) Impact of different IFS microphysics on a warm conveyor belt and the downstream flow evolution. Q J R Meteorol Soc 142(700):2727–2739. https://doi.org/10.1002/qj.2863
Joos H, Wernli H (2012) Influence of microphysical processes on the potential vorticity development in a warm conveyor belt: a case-study with the limited-area model COSMO. Q J R Meteorol Soc 138:407–418. https://doi.org/10.1002/qj.934
Lagouvardos K, Lemaitre Y, Scialom G (1993) Importance of diabatic processes on ageostrophic circulations observed during the FRONTS 87 experiment. Q J R Meteorol Soc 119(514):1321–1345
Lin YL, Zhang JS, Li XR, Deng Y (2018) Response of eddy activities to localized diabatic heating in held-suarez simulations. Clim Dyn 51:3421–3434. https://doi.org/10.1007/s00382-018-4088-4
Luo YL, Wang H, Zhang RH, Qian WM, Luo ZZ (2013) Comparison of rainfall characteristics and convective properties of monsoon precipitation systems over South China and the Yangtze and Huai River Basin. J Clim 26:110–132
Mak M, Bannon PB (1984) Frontogenesis in a moist semi-geostrophic model. J Atmos Sci 41:3485–3500. https://doi.org/10.1175/1520-0469(1984)041<3485:FIAMSM>2.0.CO;2
Mak M, Lu Y, Deng Y (2017) Two issues concerning surface frontogenesis. J Atmos Sci 74(9):2967–2987. https://doi.org/10.1175/JAS-D-16-0171.1
Ninomiya K (1984) Characteristics of baiu front as a predominant subtropical front in the summer northern hemisphere. J Meteorol Soc Jpn 62(6):880–894
Ninomiya K, Akiyama T (1992) Multi-scale features of baiu, the summer monsoon over japan and the east asia. J Meteorol Soc Jpn 70:467–495. https://doi.org/10.2151/jmsj1965.70.1B_467
Parker DJ, Thorpe AJ (1995) The role of snow sublimation in frontogenesis. Q J R Meteorol Soc 121(524):763–782
Shen Y, Zhao P, Pan Y, Yu JJ (2014) A high spatiotemporal gauge-satellite merged precipitation analysis over China. J Geophys Res Atmos 119(6):3063–3075
Thorpe AJ, Emanuel KA (1985) Frontogenesis in the presence of small stability to slantwise convection. J Atmos Sci 42(17):1809–1824
Wang CC, Chen GTJ, Ho KH (2016) A diagnostic case study of Mei-Yu frontal retreat and associated low development near Taiwan. Mon Weather Rev 144(6):2327–2349. https://doi.org/10.1175/MWR-D-15-0391.1
Yang S, Gao ST, Lu CG (2014) A generalized frontogenesis function and its application. Adv Atmos Sci 31(5):1065–1078. https://doi.org/10.1007/s00376-014-3228-y
Yang S, Gao ST, Lu CG (2015) Investigation of the mei-yu front using a new deformation frontogenesis function. Adv Atmos Sci 32(5):635–647. https://doi.org/10.1007/s00376-014-4147-7
Zhang J, Tan ZM (2009) A simulation study of the mesoscale convective systems associated with a Meiyu frontal heavy rain event. J Meteorol Res 23(4):438–454
Zhou YS, Gao ST, Shen SSP (2004) A diagnostic study of formation and structures of the Meiyu front system over East Asia. J Meteorol Soc Jpn 82(6):1565–1576
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant Nos. 41620104009, 41905071, 91637211 and 41775071) and the National Key R&D Program of China (2018YFC1507200). Yi Deng is in part supported by the U.S. National Science Foundation through Grants AGS-1354402 and AGS-1445956.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, Y., Deng, Y., Lin, Y. et al. Dynamics of the spatiotemporal morphology of Mei-yu fronts: an initial survey. Clim Dyn 56, 2715–2728 (2021). https://doi.org/10.1007/s00382-020-05619-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-020-05619-2