Skip to main content
SpringerLink
Log in

Planetary scale selection of the Madden–Julian Oscillation in an air-sea coupled dynamic moisture model

  • Published:
Climate Dynamics Aims and scope Submit manuscript

Abstract

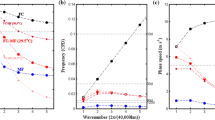
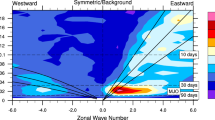
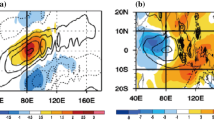
The authors present an air–sea coupled dynamic moisture (ASDM) model to explore the mechanism of preferred planetary scale of the Madden–Julian Oscillation (MJO). This ASDM model, extended from the original frictionally coupled dynamic moisture model and a mixed layer model, can present a good simulation of planetary-scale characteristics of the MJO, including a slow eastward propagation of 5 m s−1, coupled Rossby–Kelvin wave-like structure, and phase leading of convective center by warm sea surface temperature (SST). It is interesting that the planetary-scale selection in terms of instability is only found in the nonlinear ASDM model with the assumption of positive-only heating. Such a scale selection, however, cannot be found in the ASDM model with linear heating or in an uncoupled atmosphere model. The essential mechanism for the scale selection is nonlinear positive-only heating, and the air-sea interaction primarily provides an instability source to support this scale selection. This scale selection is attributed to different phase speeds of coupled moist Rossby–Kelvin waves and dry Kelvin waves. From short-wave initial perturbations, the easterly wind anomalies of eastward-propagating dry Kelvin waves from a stronger wave component will catch up with other weaker moist components and suppress their westerly wind anomalies, resulting in weak SST gradient as well as reduced moisture convergence and precipitation for these suppressed components. As a result, the wavenumber-one structure is selected. The Warm Pool-like mean state will select the stronger component among the initial short-wave perturbations and accelerate this scale selection process. These results provide new insight into MJO mechanism in terms of air-sea interaction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  • Adames ÁF, Wallace JM (2014) Three-dimensional structure and evolution of the MJO and its relation to the mean flow. J Atmos Sci 71:2007–2026

    Article  Google Scholar 

  • Adames ÁF, Kim D (2016) The MJO as a dispersive, convectively coupled moisture wave: theory and observations. J Atmos Sci 73:913–941

    Article  Google Scholar 

  • Betts AK (1986) A new convective adjustment scheme. Part I: observational and theoretical basis. Q J R Meteorol Soc 112:677–691

    Google Scholar 

  • Betts AK, Miller MT (1986) A new convective adjustment scheme. Part II: single column tests using GATE wave, BOMEX, ATEX and arctic air-mass data sets. Q J R Meteorol Soc 112:693–709

    Google Scholar 

  • Davey MK, Gill AE (1987) Experiments on tropical circulation with a simple moist model. Quart J R Meteorol Soc 113:1237–1269

    Article  Google Scholar 

  • De Szoeke SP, Edson JB, Marion JR, Fairall CW, Bariteau L (2015) The MJO and air–sea interaction in TOGA COARE and DYNAMO. J Clim 28:597–622

    Article  Google Scholar 

  • DeMott CA, Stan C, Randall DA, Branson MD (2014) Intraseasonal variability in coupled GCMs: the roles of ocean feedbacks and model physics. J Clim 27:4970–4995

    Article  Google Scholar 

  • DeMott CA, Klingaman NP, Woolnough SJ (2015) Atmosphere-ocean coupled processes in the Madden–Julian oscillation. Rev Geophys 53:1099–1154

    Article  Google Scholar 

  • DeMott CA, Benedict JJ, Klingaman NP, Woolnough SJ, Randall DA (2016) Diagnosing ocean feedbacks to the MJO: SST-modulated surface fluxes and the moist static energy budget. J Geophys Res Atmos 121:8350–8373

    Article  Google Scholar 

  • Flatau M, Flatau PJ, Phoebus P, Niiler PP (1997) The feedback between equatorial convectionand local radiation and evaporative processes: the implicatios for intraseasonal oscillations. J Atmos Sci 54:2373–2386

    Article  Google Scholar 

  • Fu X, Wang B, Li T, McCreary J (2003) Coupling between northward propagating ISO and SST in the Indian Ocean. J Atmos Sci 60:1733–1753

    Article  Google Scholar 

  • Fu X, Wang W, Lee J-Y, Wang B, Kikuchi K, Xu J, Li J, Weaver S (2015) Distinctive roles of air–sea coupling on different MJO events: a New perspective revealed from the DYNAMO/CINDY field campaign. Mon Weather Rev 143:794–812

    Article  Google Scholar 

  • Gill AE (1980) Some simple solutions for heat-induced tropical circulation. Q J R Meteorol Soc 106:447–462

    Article  Google Scholar 

  • Hendon HH, Salby ML (1994) The life cycle of the Madden–Julian oscillation. J Atmos Sci 51:2225–2237

    Article  Google Scholar 

  • Hirst AC (1986) Unstable and damped equatorial modes in simple coupled ocean–atmosphere models. J Atmos Sci 43:606–630

    Article  Google Scholar 

  • Hsu P-C, Li T (2012) Role of the boundary layer moisture asymmetry in causing the eastward propagation of the Madden–Julian oscillation. J Clim 25:4914–4931

    Article  Google Scholar 

  • Inness PM, Slingo JM (2003) Simulation of Madden–Julian oscillation in a coupled general circulation model. Part I: comparasion with observations and an atmosphere-only GCM. J Clim 16:345–364

    Article  Google Scholar 

  • Kang I-S, Liu F, Ahn M-S, Yang Y-M, Wang B (2013) The role of SST structure in convectively coupled Kelvin–Rossby waves and its implications for MJO formation. J Clim 26:5915–5930

    Article  Google Scholar 

  • Kiladis GN, Wheeler MC, Haertel PT, Straub KH, Roundy PE (2009) Convectively coupled equatorial waves. Rev Geophys 47:RG2003. doi:10.1029/2008RG000266

    Article  Google Scholar 

  • Knutson TR, Weickmann KM (1987) 30–60 day atmospheric oscillations: composite life cycles of convection and circulation anomalies. Mon Weather Rev 115:1407–1436

    Article  Google Scholar 

  • Knutson TR, Weickmann KM, Kutzbach JE (1986) Global-scale intraseasonal oscillation of outgoing longwave radiation and 250 mb zonal wind during nothern hemisphere summer. Mon Weather Rev 114:605–623

    Article  Google Scholar 

  • Lau K-M, Peng L (1987) Origin of low-frequency (intraseasonal) oscillations in the tropical atmosphere. Part I: basic theory. J Atmos Sci 44:950–972

    Article  Google Scholar 

  • Lau K-M, Sui C-H (1997) Mechanisms of short-term sea surface temperature regulation: observations during TOGA COARE. J Clim 10:465–472

    Article  Google Scholar 

  • Li T (2014) Recent advance in understanding the dynamics of the Madden–Julian oscillation. J Meteorol Res 28:1–33

    Google Scholar 

  • Li T, Wang B (1994) The influence of sea surface temperature on the tropical intraseasonal oscillation: a numerical study. Mon Weather Rev 122:2349–2362

    Article  Google Scholar 

  • Li T, Zhou C (2009) Planetary scale selection of the Madden–Julian oscillation. J Atmos Sci 66:2429–2443

    Article  Google Scholar 

  • Li T, F Tam, X Fu, T Zhou, and W Zhu (2008) Causes of the intraseasonal SST variability in the tropical indian ocean. Atmos Ocean Sci Lett 1:18–23

    Google Scholar 

  • Lim H, Lim T-K, Chang C-P (1990) Reexamination of wave-CISK theory: exsistence and properties of nonlinear wave-CISK modes. J Atmos Sci 47:3078–3091

    Article  Google Scholar 

  • Lindzen RS, Nigam S (1987) On the role of sea surface temperature gradients in forcing low-level winds and convergence in the tropics. J Atmos Sci 44:2418–2436

    Article  Google Scholar 

  • Liu F, Wang B (2012) A frictional skeleton model for the Madden–Julian oscillation. J Atmos Sci 69:2749–2758

    Article  Google Scholar 

  • Liu F, Wang B (2013) An air-sea coupled skeleton model for the Madden–Julian oscillation. J Atmos Sci 70:3147–3156

    Article  Google Scholar 

  • Liu F, Wang B (2016a) Effects of moisture feedback in a frictional coupled Kelvin–Rossby wave model and implication in the Madden-Julian oscillation dynamics. Clim Dyn. doi:10.1007/s00382-016-3090-y

    Google Scholar 

  • Liu F, Wang B (2016b) Role of horizontal advection of seasonal-mean moisture in the Madden–Julian oscillation: a theoretical model analysis. J Clim. doi:10.1175/JCLI-D-16-0078.1 (press)

    Google Scholar 

  • Madden RA, Julian PR (1971) Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J Atmos Sci 28:702–708

    Article  Google Scholar 

  • Madden RA, Julian PR (1972) Description of global-scale circulation cells in the tropics with a 40–50 day period. J Atmos Sci 29:1109–1123

    Article  Google Scholar 

  • Madden RA, Julian PR (1994) Observations of the 40-50-day tropical oscillation—a review. Mon Weather Rev 122:814–837

    Article  Google Scholar 

  • Majda AJ, Stechmann SN (2009) The skeleton of tropical intraseasonal oscillations. Proc Natl Acad Sci 106:8417–8422

    Article  Google Scholar 

  • Maloney ED, Sobel AH (2007) Idealized hot spot experiments with a general circulation model. J Clim 20:908–925

    Article  Google Scholar 

  • Maloney ED, Sobel AH, Hannah WM (2010) Intraseasonal variability in an aquaplanet general circulation model. J Adv Model Earth Syst 2:1–24

    Article  Google Scholar 

  • Matsuno T (1966) Quasi-geostrophic motions in the equatorial area. J Meteorol Soc Jpn 44:25–43

    Article  Google Scholar 

  • Miura H, Satoh M, Katsumata M (2009) Spontaneous onset of a Madden–Julian oscillation event in a cloud-system-resolving simulation. Geophys Res Lett 36:L13802. doi:10.1029/2009GL039056

    Article  Google Scholar 

  • Philander SGH, Yamagata T, Pacanowski RC (1984) Unstable air–sea interaction in the tropics. J Atmos Sci 41:604–613

    Article  Google Scholar 

  • Rui H, Wang B (1990) Development characteristics and dynamic structure of tropical intraseasonal convection anomalies. J Atmos Sci 47:357–379

    Article  Google Scholar 

  • Seiki A, Nagura M, Hasegawa T (2015) Seasonal onset of the Madden–Julian oscillation and its relation to the southeastern Indian Ocean cooling. J Meteorol Soc Jpn 93A:139–156. doi:10.2151/jmsj.2015-047

    Article  Google Scholar 

  • Sobel AH, Gildor H (2003) A simple time-dependent model of SST hot spots. J Clim 16:3978–3992

    Article  Google Scholar 

  • Sobel A, Maloney E (2012) An idealized semi-empirical framework for modeling the Madden–Julian oscillation. J Atmos Sci 69:1691–1705

    Article  Google Scholar 

  • Sobel A, Maloney E (2013) Moisture modes and the eastward propagation of the MJO. J Atmos Sci 70:187–192

    Article  Google Scholar 

  • Tomasi C (1984) Vertical distribution features of atmospheric water vapor in the Mediterranean, Red Sea, and Indian Ocean. J Geophy Res Atmos (1984–2012) 89:2563–2566

    Article  Google Scholar 

  • Waliser DE, Lau KM, Kim J-H (1999) The influence of coupled sea surface temperature on the Madde–Julian oscillation: a model perturbation experiment. J Atmos Sci 56:333–357

    Article  Google Scholar 

  • Wang B (1988a) Dynamics of tropical low-frequency waves: an analysis of the moist Kelvin wave. J Atmos Sci 45:2051–2065

    Article  Google Scholar 

  • Wang B (1988b) Comments on “an air–sea interaction model of intraseasonal oscillation in the tropics”*. J Atmos Sci 45:3521–3525

    Article  Google Scholar 

  • Wang B, Chen G (2016) A general theoretical framework for understanding essential dynamics of Madden–Julian oscillation. Clim Dyn. doi:10.1007/s00382-016-3448-1

    Google Scholar 

  • Wang B, Li T (1994) Convective interaction with boundary-layer dynamics in the development of a tropical intraseasonal system. J Atmos Sci 51:1386–1400

    Article  Google Scholar 

  • Wang B, Rui H (1990) Dynamics of the coupled moist Kelvin–Rossby wave on an equatorial β-plane. J Atmos Sci 47:397–413

    Article  Google Scholar 

  • Wang B, Xie X (1998) Coupled modes of the warm pool climate system. Part I: the role of air-sea interaction in maintaining Madden–Julian oscillation. J Clim 11:2116–2135

    Article  Google Scholar 

  • Wang B, Xue Y (1992) Behavior of a moist Kelvin wave packet with nonlinear heating. J Atmos Sci 49:549–559

    Article  Google Scholar 

  • Wang B, Li T, Chang P (1995) An intermediate model of the tropical Pacific Ocean. J Phys Oceanogr 25:1599–1616

    Article  Google Scholar 

  • Wang B, Liu F, Chen G (2016) A trio-interaction theory for Madden–Julian oscillation. Geosci Lett doi:10.1186/s40562-016-0066-z

    Google Scholar 

  • Webber BGM, Matthews AJ, Heywood KJ (2010) A dynamical ocean feedback mechanism for the Madden–Julian oscillation. Q J R Meteorol Soc 136:740–754

    Google Scholar 

  • Webber BGM, Matthews AJ, Heywood KJ, Stevens DP (2012) Ocean Rossby waves as a triggering mechanism for primary Madden–Julian events. Quart J R Meteorol Soc 138:514–527

    Article  Google Scholar 

  • Wheeler M, Kiladis GN (1999) Convectively coupled equatorial waves: analysis of clouds and temperature in the wavenumber-frequency domain. J Atmos Sci 56:374–399

    Article  Google Scholar 

  • Yang G-Y, Hoskins B, Slingo J (2003) Convectively coupled equatorial waves: a new methodology for identifying waves structures in observational data. J Atmos Sci 60:1637–1654

    Article  Google Scholar 

  • Zebiak SE (1986) Atmospheric convergence feedback in a simple model for El Niño. Mon Weather Rev 114:1263–1271

    Article  Google Scholar 

  • Zhang C (1996) Atmospheric intraseasonal variability at the surface in the tropical western Pacific Ocean. J Atmos Sci 53:739–758

    Article  Google Scholar 

  • Zhang C (2005) Madden–Julian oscillation. Rev Geophys 43:1–36

    Google Scholar 

Download references

Acknowledgements

This work was supported by the China National 973 Project (2015CB453200), the National Natural Scientific Foundation of China (41230420), the NSFC Innovative Group Grant (41421005), the grants from the IPOVAR Project (GASI-IPOVAI-01-02, GASI-IPOVAI-02), the NSFC-Shandong Joint Fund for Marine Science Research Centers (U1406401), the Strategic Priority Research Program of the Chinese Academy of Sciences (XDA11010303), the National Natural Science Foundation of China (41420104002), and the Natural Science Foundation of Jiangsu province (BK20150907). This paper is ESMC Contribution no. 169.

Author information

Authors and Affiliations

  1. Key Laboratory of Ocean Circulation and Waves, Institute of Oceanology, Chinese Academy of Sciences, Qingdao, 266071, China

    Yuntao Wei & Mu Mu

  2. University of Chinese Academy of Sciences, Beijing, 100049, China

    Yuntao Wei

  3. Earth System Modeling Center and Climate Dynamics Research Center, Nanjing University of Information Science and Technology, Nanjing, 210044, China

    Fei Liu

  4. Laboratory for Ocean and Climate Dynamics, Qingdao National Laboratory for Marine Science and Technology, Qingdao, 266237, China

    Mu Mu

  5. Laboratory for Climate Studies & CMA-NJU Joint Laboratory for Climate Prediction Studies, National Climate Center, China Meteorological Administration, Beijing, 100081, China

    Yuntao Wei & Hong-Li Ren

Authors
  1. Yuntao Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mu Mu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hong-Li Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fei Liu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wei, Y., Liu, F., Mu, M. et al. Planetary scale selection of the Madden–Julian Oscillation in an air-sea coupled dynamic moisture model. Clim Dyn 50, 3441–3456 (2018). https://doi.org/10.1007/s00382-017-3816-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00382-017-3816-5

Keywords

Search

Navigation