Studying propagation of wave in metal foam cylindrical shells with graded porosities resting on variable elastic substrate

Abstract

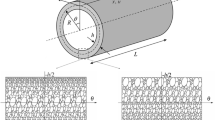
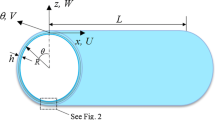
This investigation deals with wave propagation analysis of porous metal foam cylindrical shells resting on the variable elastic substrate within the framework of the first-order shear deformation shell theory. Magnesium, nickel, titanium and tungsten foams are considered as constitutive materials of cylindrical shell. The pores are distributed through the thickness uniformly, symmetrically and asymmetrically. The principle of Hamilton is employed in order to reach motion equations of porous metal foam cylindrical shell. Next, governing equations of porous metal foam are derived for a first-order shear deformation shell and then solved analytically. The effects of various parameters including porosity coefficient, various types of porosity distribution, length-to-thickness ratio, radius-to-thickness ratio, circumferential wave number, Pasternak coefficient and variable Winkler coefficient on the variation of wave frequency and phase velocity of metal foam cylindrical shells are covered and presented within the framework of a group of figures which can be seen in detail.

Appendix

The components of stiffness and mass matrices are as follows:

$$\begin{aligned} K_{11} & = - A_{11} k_{x}^{2} - \frac{{A_{66} }}{{R^{2} }}k_{n}^{2} ,K_{12} = - k_{x} k_{n} \left( {\frac{{A_{12} + A_{66} }}{R}} \right),K_{13} = \frac{{A_{12} }}{R}k_{x} i, \\ K_{14} & = - B_{11} k_{x}^{2} - \frac{{B_{66} }}{{R^{2} }}k_{n}^{2} ,\,\,K_{15} = - k_{x} k_{n} \left( {\frac{{B_{12} + B_{66} }}{R}} \right),K_{22} = - A_{66} k_{x}^{2} - \frac{{A_{11} }}{{R^{2} }}k_{n}^{2} - \frac{{A_{55}^{s} }}{{R^{2} }}, \\ K_{23} & = k_{n} (\frac{{A_{11} + A_{55}^{s} }}{{R^{2} }})i,\,\,K_{24} = - k_{x} k_{n} \left( {\frac{{B_{12} + B_{66} }}{R}} \right),K_{25} = - B_{66} k_{x}^{2} - \frac{{B_{11} }}{{R^{2} }}k_{n}^{2} - \frac{{A_{55}^{s} }}{R}, \\ K_{33} & = - A_{55}^{s} k_{x}^{2} - \left( {\frac{{A_{11} }}{{R^{2} }} + k_{n}^{2} \frac{{A_{55}^{s} }}{{R^{2} }}} \right) - k_{w} - k_{p} \left( {k_{x}^{2} + \frac{{k_{n}^{2} }}{{R^{2} }}} \right),K_{34} = \left( {A_{55}^{s} - \frac{{B_{12} }}{R}} \right)ik_{x} ,\,\,K_{35} = k_{n} \left( {\frac{{A_{55}^{s} }}{R} - \frac{{B_{11} }}{{R^{2} }}} \right)i, \\ K_{44} & = - D_{11} k_{x}^{2} - k_{n}^{2} \frac{{D_{66} }}{{R^{2} }} - A_{55}^{s} ,K_{45} = - k_{x} k_{n} \frac{{D_{12} + D_{66} }}{R},\,\,K_{55} = - D_{66} k_{x}^{2} - k_{n}^{2} \frac{{D_{11} }}{{R^{2} }} - A_{55}^{s} \\ \end{aligned}$$

$$\begin{aligned} M_{11} & = M_{22} = M_{33} = I_{0} , \\ M_{14} & = M_{25} = I_{1} , \\ M_{44} & = M_{55} = I_{2} \\ \end{aligned}$$