Skip to main content
SpringerLink
Log in

Vibration analysis of polymer composite plates reinforced with graphene platelets resting on two-parameter viscoelastic foundation

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

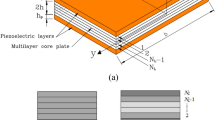
In this paper, the vibration behavior of composite plate reinforced with graphene platelets (GPLs) resting on viscoelastic foundation in thermal environment based on higher-order shear deformation theory is examined. Halpin–Tsai model is utilized to determine the material properties of composites plate reinforced with GPL. In the present study, four patterns of GPLs distribution in plate layers are considered. To obtain the Euler–Lagrange equations of composites plate, Hamilton’s principle is employed and Navier’s method is utilized for analyzing and solving the problem. The results of this study have been verified by checking them with the previous works. The effects of various parameters such as geometry effect, GPL weight fraction, temperature changes and viscoelastic foundation on vibrational reaction of structure are analyzed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. Graphene platelet-reinforced composite.

References

  1. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, Grigorieva IV, Firsov A (2004) Electric filed effect in atomically thin carbon films. Science 306:666–669

    Google Scholar 

  2. Wang J, Li Z, Fan G, Pan H, Chen Z, Zhang D (2012) Reinforcement with graphene nanosheets in aluminum matrix composites. Scripta Mater 66:594–597

    Google Scholar 

  3. Chatterjee S, Wang J, Kuo W, Tai N, Salzmann C, Li W, Hollertz R, Nüesch F, Chu B (2012) Mechanical reinforcement and thermal conductivity in expanded graphene nanoplatelets reinforced epoxy composites. Chem Phys Lett 531:6–10

    Google Scholar 

  4. Adam H (1997) Carbon fibre in automotive applications. Mater Des 18(4–6):349–355

    Google Scholar 

  5. Bellucci S, Balasubramanian C, Micciulla F, Rinaldi G (2007) CNT composites for aerospace applications. J Exp Nanosci 2(3):193–206

    Google Scholar 

  6. Baradaran S, Moghaddam E, Basirun WJ, Mehrali M, Sookhakian M, Hamdi M, Nakhaei Moghaddam MR, Alias Y (2014) Mechanical properties and biomedical applications of a nanotube Hydroxyapatite reduced graphene oxide composite. Carbon 69:32–45

    Google Scholar 

  7. Gauvin F, Robert M (2015) Durability study of vinylester/silicate nanocomposites for civil engineering applications. Polym Degrad Stab 121:359–368

    Google Scholar 

  8. Ji X-Y, Cao Y-P, Feng X-Q (2010) Micromechanics prediction of the effective elastic moduli of graphene sheet-reinforced polymer nanocomposites. Model Simul Mater Sci 18(4):045005

    Google Scholar 

  9. Du X, Skachko I, Barker A, Andrei EY (2008) Approaching ballistic transport in suspended graphene. Nat Nanotechnol 3(8):491–495

    Google Scholar 

  10. Balandin AA, Ghosh S, Bao W, Calizo I, Teweldebrhan D, Miao F, Lau CN (2008) Superior thermal conductivity of single-layer graphene. Nano Lett 8(3):902–907

    Google Scholar 

  11. Lee C, Wei X, Kysar JW, Hone J (2008) Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 321(5887):385–388

    Google Scholar 

  12. Huang X, Qi X, Boey F, Zhang H (2012) Graphene-based composites. Chem Soc Rev 41(2):666–686

    Google Scholar 

  13. Rafiee MA, Rafiee J, Wang Z, Song H, Yu Z-Z, Koratkar N (2009) Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 3(12):3884–3890

    Google Scholar 

  14. Rafiee MA, Rafiee J, Yu Z-Z, Koratkar N (2009) Buckling resistant graphene nanocomposites. Appl Phys Lett 95(22):223103

    Google Scholar 

  15. Rafiee MA, Rafiee J, Srivastava I, Wang Z, Song H, Yu Z-Z, Koratkar N (2010) Fracture and fatigue in graphene nanocomposites. Small 6(2):179–183

    Google Scholar 

  16. Karami B, Janghorban M, Tounsi A (2019) Galerkin’s approach for buckling analysis of functionally graded anisotropic nanoplates/different boundary conditions. Eng Comput 35(4):1297–1316

    Google Scholar 

  17. Alimirzaei S, Mohammadimehr M, Tounsi A (2019) Nonlinear analysis of viscoelastic micro-composite beam with geometrical imperfection using FEM: MSGT electro-magneto-elastic bending, buckling and vibration solutions. Struct Eng Mech 71(5):485–502

    Google Scholar 

  18. Meksi R, Benyoucef S, Mahmoudi A, Tounsi A, Bedia EAA, Mahmoud SR (2019) An analytical solution for bending, buckling and vibration responses of FGM sandwich plates”. J Sandw Struct Mater 21(2):727–757

    Google Scholar 

  19. Hellal H, Bourada M, Hebali H, Bourada F, Tounsi A, Bousahla AA, Mahmoud SR (2019) Dynamic and stability analysis of functionally graded material sandwich plates in hygro-thermal environment using a simple higher shear deformation theory. J Sandw Struct Mater 1:1–38

    Google Scholar 

  20. Semmah A, Heireche H, Bousahla AA, Tounsi T (2019) Thermal buckling analysis of SWBNNT on Winkler foundation by non local FSDT. Adv Nano Res 7(2):89–98

    Google Scholar 

  21. Hussain M, Naeem MN, Tounsi A, Taj M (2019) Nonlocal effect on the vibration of armchair and zigzag SWCNTs with bending rigidity. Adv Nano Res 7(6):431–442

    Google Scholar 

  22. Boutaleb S, Benrahou KH, Bakora A, Algarni A, Bousahla AA, Tounsi A, Tounsi A, Mahmoud SR (2019) Dynamic analysis of nanosize FG rectangular plates based on simple nonlocal quasi 3D HSDT. Adv Nano Res 7(3):191–208

    Google Scholar 

  23. Tlidji Y, Zidou M, Draiche K, Safa A, Bourada M, Tounsi A, Bousahla AA, Mahmoud SR (2019) Vibration analysis of different material distributions of functionally graded microbeam. Struct Eng Mech 69(6):637–649

    Google Scholar 

  24. Medani M, Benahmed A, Zidour M, Heireche H, Tounsi A, Bousahla AA, Tounsi A, Mahmoud SR (2019) Static and dynamic behavior of (FG-CNT) reinforced porous sandwich plate. Steel Compos Struct 32(5):595–610

    Google Scholar 

  25. Berghouti H, Adda BEA, Benkhedda A, Tounsi A, Berghouti B et al (2019) Vibration analysis of nonlocal porous nanobeams made of functionally graded material. Adv Nano Res 7(5):351–364

    Google Scholar 

  26. Draoui A, Mohamed Zidour M, Abdelouahed Tounsi T, Adim B (2019) Static and dynamic behavior of nanotubes-reinforced sandwich plates using (FSDT). J Nano Res 57:117–135

    Google Scholar 

  27. Adda Bedia W, Houari MSA, Bessaim A, Bousahla AA, Tounsi A, Saeed T, Alhodaly MS (2019) A new hyperbolic two-unknown beam model for bending and buckling analysis of a nonlocal strain gradien nanobeams. J Nano Res 57:175–191

    Google Scholar 

  28. Karami M, Janghorban M, Tounsi A (2019) On pre stressed functionally graded anisotropic nanoshell in magnetic field. Journal of the Brazilian Society of Mechanical Sciences and Engineering 41:495

    Google Scholar 

  29. Karami M, Janghorban M, Tounsi A (2019) Wave propagation of functionally graded anisotropic nanoplates resting on Winkler-Pasternak foundation. Struct Eng Mech 7(1):55–66

    Google Scholar 

  30. Karami M, Shahsavari D, Janghorban M, Tounsi A (2019) Resonance behavior of functionally graded polymer composite Nano plates reinforced with grapheme Nano platelets. Int J Mech Sci 156:94–105

    Google Scholar 

  31. Karami M, Janghorban M, Tounsi A (2019) On exact wave propagation analysis of triclinic material using three dimensional bi-Helmholtz gradient plate model. Struct Eng Mech 69(5):487–497

    Google Scholar 

  32. Draiche K, Bousahla AA, Tounsi A, Alwabli AS, Tounsi A, Mahmoud SR (2019) Static analysis of laminated reinforced composite plates using a simple first-order shear deformation theory. Comput Concrete 24(4):369–378

    Google Scholar 

  33. Chaabane LL, Bourada F, Sekkal M, Zerouati S, Zaoui FZ, Tounsi A, Derras A, Bousahla AA, Tounsi A (2019) Analytical study of bending and free vibration responses of functionally graded beams resting on elastic foundation. Struct Eng Mech 71(2):185–196

    Google Scholar 

  34. Abualnour M, Chikh A, Hebali H, Kaci A, Tounsi A, Bousahla AA, Tounsi A (2019) Thermomechanical analysis of antisymmetric laminated reinforced composite plates using a new four variable trigonometric refined plate theory. Comput Concr 24(6):1

    Google Scholar 

  35. Belbachir N, Draich K, Bousahla AA, Bourada M, Tounsi A, Mohammadimehr M (2019) Bending analysis of anti-symmetric cross-ply laminated plates under nonlinear thermal and mechanical loadings. Steel Compos Struct 33(1):913–924

    Google Scholar 

  36. Batou B, Nebab M, Bennai R, Atmane HA, Tounsi A, Bouremana A (2019) Wave dispersion properties in imperfect sigmoid plates using various HSDTs. Steel Compos Struct 33(5):699–716

    Google Scholar 

  37. Bourada F, Bousahla AA, Bourada M, Azzaz A, Zinata A, Tounsi A (2019) Dynamic investigation of porous functionally graded beam using a sinusoidal shear deformation theory. Wind Struct 28(1):19–30

    Google Scholar 

  38. Sahla M, Saidi H, Draiche K, Bousahla AA, Fouad Bourada F, Tounsi A (2019) Free vibration analysis of angle-ply laminated composite and soft core sandwich plates. Steel Compos Struct 33(5):663–679

    Google Scholar 

  39. Khiloun M, Bousahla AA, Abdelhakim Kaci A, Aicha Bessaim A, Tounsi A, Mahmoud SR (2019) Analytical modeling of bending and vibration of thick advanced composite plates using a four-variable quasi 3D HSDT”. Eng Comput 1:1–15

    Google Scholar 

  40. Addou FY, Meradjah M, Bousahla AA, Benachour A, Bourada F, Tounsi A, Mahmoud SR (2019) Influences of porosity on dynamic response of FG plates resting on Winkler/Pasternak/Kerr foundation using quasi 3D HSDT. Comput Concr 24(4):347–367

    Google Scholar 

  41. Boutaleb S, Benrahou KH, Bakora A, Algarni A, Bousahla AA, Abdelouahed Tounsi A, Tounsi A, Mahmoud SR (2019) Dynamic Analysis of nanosize FG rectangular plates based on simple nonlocal quasi 3D HSDT. Adv Nano Res 7(3):189–206

    Google Scholar 

  42. Zarga D, Tounsi A, Bousahla AA, Bourada F, Mahmoud SR (2018) Thermomechanical bending study for functionally graded sandwich plates using a simple quasi-3D shear deformation theory. Steel Compos Struct 32(3):389–410

    Google Scholar 

  43. Boulefrakh L, Habib H, Abdelbaki C, Bousahla AA, Tounsi A, Mahmoud SR (2019) The effect of parameters of visco -Pasternak foundation on the bending and vibration properties of a thick FG plate”. Geomechanics and Engineering 18(2):161–178

    Google Scholar 

  44. Boukhlif Z, Bouremana M, Bourada F, Bousahla AA, Bourada M, Tounsi A, Al-Osta MA (2019) A simple quasi-3D HSDT for the dynamics analysis of FG thick plate on elastic foundation. Steel Compos Struct 31(5):503–516

    Google Scholar 

  45. Mahmoudi A, Samir Benyoucef S, Abdelouahed Tounsi A, Abdelkader Benachour A, Adda Bedia EAA, Mahmoud SR (2019) A refined quasi-3D shear deformation theory for thermo-mechanical behavior of functionally graded sandwich plates on elastic foundations”. J Sandw Struct Mater 21(6):1906–1926

    Google Scholar 

  46. Zaoui FZ, Ouinas D, Tounsi A (2019) New 2D and quasi-3D shear deformation theories for free vibration of functionally graded plates on elastic foundations. Compos Part B Eng 159:231–247

    Google Scholar 

  47. Chandra Y, Chowdhury R, Scarpa F, Adhikari S, Sienz J, Arnold C, Murmu T, Bould D (2012) Vibration frequency of graphene based composites: a multiscale approach. Mater Sci Eng B 177(3):303–310

    Google Scholar 

  48. Song M, Kitipornchai S, Yang J (2017) Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos Struct 159:579–588

    Google Scholar 

  49. Yang J, Wu H, Kitipornchai S (2017) Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos Struct 140:110–119

    Google Scholar 

  50. Feng C, Kitipornchai S, Yang J (2017) Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng Struct 170:80–90

    Google Scholar 

  51. Potts JR, Dreyer DR, Bielawski CW, Ruoff RS (2011) Graphene-based polymer nanocomposites. Polymer 52(1):5–25

    Google Scholar 

  52. Shen HS, Xiang Y, Lin F (2017) Nonlinear vibration of functionally graded graphene-reinforced composite laminated plates in thermal environments. Compos Struct 319:175–193

    MathSciNet  MATH  Google Scholar 

  53. Shen HS, Xiang Y, Lin F (2017) Nonlinear bending of functionally graded graphene-reinforced composite laminated plates resting on elastic foundations in thermal environments. Compos Struct

Download references

Author information

Authors and Affiliations

  1. Department of Mechanics, Faculty of Engineering, Imam Khomeini International University, Qazvin, 3414916818, Iran

    Saeedeh Qaderi & Farzad Ebrahimi

Authors
  1. Saeedeh Qaderi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Farzad Ebrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Farzad Ebrahimi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

  • 1.

    $$ {\text{K}}_{11} = - m^{2} A_{11} - n^{2} \left( {A_{44} } \right) $$

  • 2.

    $$ K_{12} = - mnA_{12} - mnA_{44} $$

  • 3.

    $$ K_{13} = c_{1} m^{3} \left( {D_{11} } \right) + c_{1} n^{2} m\left( {D_{12} } \right) + 2c_{1} mn^{2} \left( {D_{44} } \right) $$

  • 4.

    $$ K_{14} = - m^{2} \left( {B_{11} } \right) + c_{1} m^{2} \left( {D_{11} } \right) + c_{1} n^{2} \left( {D_{44} } \right) - n^{2} B_{44} $$

  • 5.

    $$ K_{15} = mnc_{1} D_{12} - mnB_{44} + mnc_{1} D_{44} - mnB_{12} $$

  • 6.

    $$ K_{21} = K_{12} $$

  • 7.

    $$ K_{22} = - n^{2} A_{22} - m^{2} A_{44} $$

  • 8.

    $$ K_{23} = c_{1} n^{3} D_{22} + mn^{2} c_{1} D_{12} + 2m^{2} nc_{1} D_{44} $$

  • 9.

    $$ K_{24} = - mnB_{12} + c_{1} mnD_{12} - mnB_{44} c_{1} mnD_{44} $$

  • 10.

    $$ K_{25} = - n^{2} B_{22} + c_{1} n^{2} D_{22} - m^{2} B_{44} + C_{1} m^{2} B_{44} $$

  • 11.

    $$ K_{31} = K_{13} $$

  • 12.

    $$ K_{32} = K_{23} $$

  • 13.

    $$ K_{33} = - m^{4} c_{1}^{2} G_{12} + n^{2} m^{2} \left( { - 2c_{1}^{2} G_{12} - 4c_{1}^{2} G_{44} } \right) - n^{4} c_{1}^{2} G_{22} - m^{2} \left( {A_{55} - 6c_{1} C_{55} + 9c_{1}^{2} E_{55} } \right) - n^{2} \left( {A_{66} - 6c_{1} C_{66} + 9c_{1}^{2} E_{66} } \right) - K_{w} + K_{p} \left( { - n^{2} - m^{2} } \right) + N_{T} \left( {m^{2} + n^{2} } \right) $$

  • 14.

    $$ K_{34} = c_{1} m^{3} E_{11} - c_{1}^{2} m^{3} G_{11} + mn^{2} \left( {c_{1} E_{12} - c_{1}^{2} G_{12} + 2c_{1} E_{44} - 2c_{1}^{2} G_{44} } \right) - 3c_{1} mA_{55} C_{55} + 3c_{1} m\left( {C_{55} - 3c_{1} E_{55} } \right) $$

  • 15.

    $$ K_{35} = m^{2} n\left( { - c_{1}^{2} G_{12} + 2c_{1} E_{44} - 2c_{1}^{2} G_{44} + c_{1} E_{12} } \right) - n^{3} c_{1}^{2} G_{22} - 3c_{1} nA_{66} C_{66} + 3c_{1} n\left( {C_{66} - 3c_{1} E_{66} } \right) + c_{1} n^{3} E_{22} $$

  • 16.

    $$ K_{41} = K_{14} $$

  • 17.

    $$ K_{42} = K_{24} $$

  • 18.

    $$ K_{43} = K_{34} $$

  • 19.

    $$ K_{44} = - m^{2} \left( {C_{11} - 2c_{1} E_{11} + c_{1}^{2} G_{11} } \right) - n^{2} (C_{44} - 2c_{1} E_{44} + c_{1}^{2} G_{44} + 3c_{1} \left( {C_{55} - 3c_{1} E_{55} } \right) - 3c_{1} A_{55} C_{55} $$

  • 20.

    $$ K_{45} = - mn(c_{1} E_{12} + C_{44} - c_{1} E_{44} + c_{1}^{2} G_{12} - c_{1} E_{44} + c_{1}^{2} G_{44} + C_{12} - c_{1} E_{12} $$

  • 21.

    $$ K_{51} = K_{15} $$

  • 22.

    $$ K_{52} = K_{25} $$

  • 23.

    $$ K_{53} = K_{35} $$

  • 24.

    $$ K_{54} = K_{45} $$

  • 25.

    $$ K_{55} = - n^{2} \left( {C_{22} - 2c_{1} E_{22} + c_{1}^{2} G_{22} } \right) - m^{2} \left( {C_{44} - 2c_{1} E_{44} c_{1}^{2} G_{44} } \right) + 3c_{1} C_{66} - A_{66} + 3c_{1} \left( {C_{66} - 3c_{1} E_{66} } \right) $$

  • 26.

    $$ M_{11} = - I_{0} $$

  • 27.

    $$ M_{12} = M_{21} = 0 $$

  • 28.

    $$ M_{13} = c_{1} mI_{3} $$

    .

  • 29.

    $$ M_{14} = - I_{1} + c_{1} I_{3} $$

  • 30.

    $$ M_{15} = M_{51} = 0 $$

  • 31.

    $$ M_{22} = - I_{0} $$

  • 32.

    $$ M_{23} = M_{32} = c_{1} nI_{3} $$

  • 33.

    $$ M_{24} = M_{42} = 0 $$

  • 34.

    $$ M_{25} = - I_{1} + c_{1} I_{3} $$

  • 35.

    $$ M_{31} = c_{1} mI_{3} $$

  • 36.

    $$ M_{32} = M_{23} $$

  • 37.

    $$ M_{33} = - I_{0} - 2c_{1}^{2} I_{6} \left( {m^{2} + n^{2} } \right) $$

  • 38.

    $$ M_{34} = M_{43} = c_{1} mI_{4} - mc_{1}^{2} I_{6} $$

  • 39.

    $$ M_{35} = c_{1} nI_{4} - nc_{1}^{2} I_{6} $$

  • 40.

    $$ M_{44} = M_{55} = - I_{2} + 2c_{1} I_{4} - c_{1}^{2} I_{6} $$

  • 41.

    $$ C_{11} = C_{12} = C_{13} = C_{14} = C_{15} = C_{21} = C_{22} = C_{23} = C_{24} = C_{25} = C_{31} = C_{32} = C_{34} = C_{35} = C_{41} = C_{42} = C_{43} = C_{44} = C_{45} = C_{51} = C_{52} = C_{53} = C_{54} = C_{55} = 0 $$

  • 42.

    $$ C_{33} = C_{d} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qaderi, S., Ebrahimi, F. Vibration analysis of polymer composite plates reinforced with graphene platelets resting on two-parameter viscoelastic foundation. Engineering with Computers 38, 419–435 (2022). https://doi.org/10.1007/s00366-020-01066-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01066-z

Keywords

Search

Navigation