Skip to main content
SpringerLink
Log in

Squeezing flow of nanofluids of Cu–water and kerosene between two parallel plates by Gegenbauer Wavelet Collocation method

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

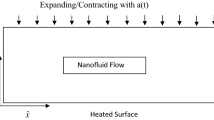
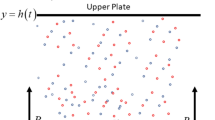
Operational matrices of Gegenbauer wavelets have significant role for approximate solution of differential equations. In the present study, approximate solutions of the squeezing nanofluids of Cu–kerosene and Cu–water between parallel plates with magnetic field are obtained by GW Collocation Method. The governing nonlinear PDEs may be turned into the nonlinear ODEs by similarity transformation. These nonlinear equations are turned into the set of linear ODEs by quasilinearization technique. The effective thermal conductivity and the effective dynamic viscosity of nanofluids have been taken as models of Maxwell–Garnetts and Brinkman. The effects of physical parameters have been displayed by graphs and tables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Stefan MJ (1874) Versuch Uberdiescheinbareadhesion. Sitzungsberichte der Akademieder Wissenschaftenin Wien, Mathematik-Naturwissen 69:713–721

    Google Scholar 

  2. Reynolds O (1886) On the theory of lubrication and its application to Mr. Beauchamp Tower’s experiments including an experimental determination of the viscosity of olive oil. Philos Trans R Soc Lond 177:157–234

    MATH  Google Scholar 

  3. Archibald FR (1956) Load capacity and time relations for squeeze films. J Lubr Technol 78:A231–A245

    Google Scholar 

  4. Hamdan MH, Baron RM (1992) Analysis of the squeezing flow of dusty fluids. Appl Sci Res 49:345–354

    MATH  Google Scholar 

  5. Rashidi MM, Shahmohamadi H, Dinarvand S (2008) Analytic approximate solutions for unsteady two-dimensional and axisymmetric squeezing flows between parallel plates. Math Probl Eng 2008:1–13

    MathSciNet  MATH  Google Scholar 

  6. Siddiqui AM, Irum S, Ansari AR (2008) Unsteady squeezing flow of a viscous MHD fluid between parallel plates. Math Modell Anal 13:565–576

    MATH  Google Scholar 

  7. Mahmood M, Asghar S, Hossain MA (2007) Squeezed flow and heat transfer over a porous surface for viscous fluid. Heat Mass Transf 44:165–173

    Google Scholar 

  8. Domairry G, Aziz A (2009) Approximate analysis of MHD squeeze flow between two parallel disks with suction or injection by homotopy perturbation method. Math Prob Eng 2009:603–616

    MATH  Google Scholar 

  9. Hayat T, Yousaf A, Mustafa M, Obaidat S (2011) MHD squeezing flow of second grade fluid between parallel disks. Int J Num Meth Fluids 69:399–410

    MathSciNet  MATH  Google Scholar 

  10. Mustafa M, Hayat T, Obaidat S (2012) On heat and mass transfer in the unsteady squeezing flow between parallel plates. Mechanica 47:1581–1589

    MathSciNet  MATH  Google Scholar 

  11. Duwairi HM, Tashtoush B, Domesh RA (2004) On heat transfer effects of a viscous fluid squeezed and extruded between parallel plates. Heat Mass Transf 14:112–117

    Google Scholar 

  12. Khaled ARA, Vafai K (2004) Hydromagnetic squeezed flow and heat transfer over a sensor surface. Int J Eng Sci 42:509–519

    MATH  Google Scholar 

  13. Qayyum A, Awais M, Alsaedi A, Hayat T (2012) Unsteady squeezing flow of jeffery fluid between two parallel disks. Chin Phys Lett 29:034701

    Google Scholar 

  14. Malvandi A, Ganji DD (2014) Magnetic field effect on nanoparticles migration and heat transfer of water/alumina nanofluid in a channel. J Mag Mag Mater 362:172–179

    Google Scholar 

  15. Hamad MAA, Pop I, Ismail MdAI (2011) Magnetic field effects on free convection flow of a nanofluid past a vertical semi-infinite flat plate. Nonlinear Anal Real World Appl. 12:1338–1346

    MathSciNet  MATH  Google Scholar 

  16. Malvandi A, Moshizi SA, Ganji DD (2014) Effect of magnetic fields on heat convection inside a concentric annulus filled with Al2O3-water nanofluid. Adv Powder Technol 25:1817–1824

    Google Scholar 

  17. Malvandi A, Ganji DD (2015) Magnetic field and slip effects on free convection inside a vertical enclosure filled with alumina/water nanofluid. Chem Eng Res Des 94:355–364

    Google Scholar 

  18. Wang X, Xu X, Choi SUS (1999) Thermal conductivity of nanoparticle-fluid mixture. J Thermophys Heat Transf 13:474–480

    Google Scholar 

  19. Mandy A (2012) Unsteady mixed convection boundary layer flow and heat transfer of nanofluids due to stretching sheet. Nucl Eng Des 249:248–255

    Google Scholar 

  20. Hatami M, Sheikholeslami M, Ganji DD (2014) Nanofluid flow and heat transfer in an asymmetric porous channel with expanding or contracting wall. J Mol Liquids 195:230–239

    Google Scholar 

  21. Hatami M, Sheikholeslami M, Hosseini M, Ganji DD (2014) Analytical investigation of MHD nanofluid flow in non-parallel walls. J Mol Liquids 194:251–259

    Google Scholar 

  22. Pourmehran O, Rahimi-Gorji M, Gorji-Bandpy M, Ganji DD (2015) Analytical investigation of squeezing unsteady nanofluid flow between parallel plates by LSM and CM. Alexandria Eng J 54:17–26

    Google Scholar 

  23. Sheikholeslami M, Soleimani S, Ganji DD (2016) Effect of electric field on hydrothermal behaviour of nanofluid in a complex geometry. J Mol Liq 213:153–161

    Google Scholar 

  24. Sheikholeslami M, Rashidi MM, Ganji DD (2015) Numerical investigation of magnetic nanofluid forced convective heat transfer in existence of variable magnetic field using two phase model. J Mol Liq 212:117–126

    Google Scholar 

  25. Sobamowo MG, Jayesimi LO (2017) Squeezing flow analysis of nanofluid under the effects of magnetic field and slip boundary using Chebychev spectral collocation method. Fluid Mech 3(6):54–60

    Google Scholar 

  26. Sheikholeslami M, Azimi M, Ganji DD (2015) Application of differential transformation method for nanofluid flow in a semipermeable channel considering magnetic field effect. J Comput Meth Eng Sci Mech 16:246–255

    Google Scholar 

  27. Sheikholeslami M, Rashidi MM, Alsaad DM, Rokni HB (2015) Steady nanofluid flow between parallel plates considering thermophoresis and Brownian effects. J King Saud Univ Sci 1:2. https://doi.org/10.1016/j.jksus.2015.06.003

    Article  Google Scholar 

  28. Sheikholeslami M, Ganji DD (2015) Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM. Comput Meth Appl Mech Eng 283:651–663

    MathSciNet  MATH  Google Scholar 

  29. Acharya N, Das K, Kundu PK (2016) The squeezing flow of Cu-water and Cu-kerosene nanofluid between two parallel plates. Alex Eng J 55:1177–1186

    Google Scholar 

  30. Sobamowo MG, Jayesimi LO, Waheed MA (2018) On the study of magnetohydrodynamic squeezing flow of nanofluid between two parallel plates embedded in a porous medium. J Comput Eng Phys Model 1(4):01–15

    Google Scholar 

  31. Noor MA, Mohyud-Din ST, Waheed A (2008) Variation of parameter method for solving fifth-order boundary value problems. Appl Math Inform Sci 2:135–141

    MathSciNet  MATH  Google Scholar 

  32. Sheikholeslami M, Ganji DD, Ashorynejad HR (2013) Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol 239:259–265

    Google Scholar 

  33. Sheikholeslami M, Ganji DD, Ashorynejad HR, Rokni HB (2012) Analytical investigation of jeffery hamel flow with high magnetic field and nanoparticle by Adomian decomposition method. Appl Math Mech Engl Ed 33:1553–1564

    MathSciNet  MATH  Google Scholar 

  34. Ellahi R, Raza M, Vafai K (2012) Series solutions of non-Newtonian nanofluids with Reynolds’ model and Vogel’s model by means of the homotopy analysis method. Math Comput Modell 55:1876–1891

    MathSciNet  MATH  Google Scholar 

  35. Sheikholeslami M, Ellahi R, Ashorynejad HR, Hayat T (2014) Effects of heat transfer in flow of nanofluids over a permeable stretching wall in a porous medium. J Comput Theor Nanosci 11:486–496

    Google Scholar 

  36. Sheikholeslami M, Ganji DD (2013) Heat transfer of Cu-water nanofluid between parallel plates. Powder Technol 235:873–879

    Google Scholar 

  37. Sheikholeslami Mohsen, Arabkoohsar Ahmad, Khan Ilyas, Shafee Ahmad, Li Zhixiong (2019) Impact of Lorentz forces on Fe3O4-water ferrofluid entropy and exergy treatment within a permeable semi annulus. J Clean Prod 221:885–898

    Google Scholar 

  38. Sheikholeslami M, Haq Rizwan-ul, Shafee Ahmad, Li Zhixiong, Elaraki Yassir G, Tlili I (2019) Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger. Int J Heat Mass Transf 135:470–478

    Google Scholar 

  39. Sheikholeslami M (2019) Omid Mahian, Enhancement of PCM solidification using inorganic nanoparticles and an external magnetic field with application in energy storage systems. J Clean Prod 215:963–977

    Google Scholar 

  40. Sheikholeslami M, Rizwan-ul Haq, Shafee A, Li Z (2019) Heat transfer behavior of Nanoparticle enhanced PCM solidification through an enclosure with V shaped fins. Int J Heat Mass Transf 130:1322–1342

    Google Scholar 

  41. Sheikholeslami M (2019) New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput Methods Appl Mech Eng 344:319–333

    MathSciNet  MATH  Google Scholar 

  42. Sheikholeslami M (2019) Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method. Comput Methods Appl Mech Eng 344:306–318

    MathSciNet  MATH  Google Scholar 

  43. Sheikholeslami M, Jafaryar M, Hedayat M, Shafee A, Li Z, Khang Nguyen T, Bakouri M (2019) Heat transfer and turbulent simulation of nanomaterial due to compound turbulator including irreversibility analysis. Int J Heat Mass Transf 137:1290–1300

    Google Scholar 

  44. Sheikholeslami M, Jafaryar M, Shafee A, Li Z, Rizwan-ul Haq (2019) Heat transfer of nanoparticles employing innovative turbulator considering entropy generation. Int J Heat Mass Transf 136:1233–1240

    Google Scholar 

  45. Sheikholeslami M, Shafee A, Rizwan-ul Haq, Shafee A, Zareei A, Rizwan-ul Haq, Li Z (2019) Heat transfer of magnetic nanoparticles through porous media including exergy analysis. J Mol Liq 279:719–732

    Google Scholar 

  46. Sheikholeslami M, Li Z, Shafee A (2018) Lorentz forces effect on NEPCM heat transfer during solidification in a porous energy storage system. Int J Heat Mass Transfer 127:665–674

    Google Scholar 

  47. Sheikholeslami M, Seyednezhad M (2018) Simulation of nanofluid flow and natural convection in a porous media under the influence of electric field using CVFEM. Int J Heat Mass Transf 120:772–781

    Google Scholar 

  48. Sheikholeslami M, Sadoughi MK (2018) Simulation of CuO-water nanofluid heat transfer enhancement in presence of melting surface. Int J Heat Mass Transf 116:909–919

    Google Scholar 

  49. Sheikholeslami M, Rokni HB (2017) Numerical modeling of nanofluid natural convection in a semi annulus in existence of Lorentz force. Comput Methods Appl Mech Eng 317:419–430

    MathSciNet  MATH  Google Scholar 

  50. Pathak A, Singh RK, Mandal BN (2014) Solution of Abel’s integral equation by using Gegenbauer wavelets. Investig Math Sci 4(1):43–52

    MATH  Google Scholar 

  51. Abd-Elhameed WM, Youssri YH (2015) New spectral solutions of multi-term fractional order initial value problems with error analysis. Comput Model Eng Sci 105(5):375–398

    Google Scholar 

  52. Abd-Elhameed WM, Youssri YH (2014) New ultraspherical wavelets spectral solutions for fractional Riccati differential equations. Abstr Appl Anal. https://doi.org/10.1155/2014/626275

    Article  MathSciNet  MATH  Google Scholar 

  53. Rehman M, Saeed U (2015) Gegenbauer wavelets operational matrix method for fractional differential equations. J Korean Math Soc 52(5):1069–1096

    MathSciNet  MATH  Google Scholar 

  54. Abd-Elhameed WM, Youssri YH, Doha EH (2014) New solutions for singular lane-emden equations arising in astrophysics based on shifted ultraspherical operational matrices of derivatives. Comput Methods Differ Equ 2(3):171–185

    MathSciNet  MATH  Google Scholar 

  55. Youssri YH, Abd-Elhameed WM, Doha EH (2015) Ultraspherical wavelets method for solving Lane-Emden type equations. Rom J Phys 60(9):1298–1314

    Google Scholar 

  56. Youssri YH, Abd-Elhameed WM, Doha EH (2015) Accurate spectral solutions of first-and second-order initial value problems by the ultraspherical wavelets-Gauss collocation method. Appl Appl Math Int J 10(2):835–851

    MathSciNet  MATH  Google Scholar 

  57. Doha EH, Abd-Elhameed WM, Youssri YH (2016) New ultraspherical wavelets collocation method for solving 2nth-order initial and boundary value problems. J Egypt Math Soc 24(2):319–327

    MathSciNet  MATH  Google Scholar 

  58. Çelik İ (2018) Generalization of Gegenbauer wavelet collocation method to the generalized Kuramoto–Sivashinsky equation. Int J Appl Comput Math 4(5):111

    MathSciNet  MATH  Google Scholar 

  59. Szegö G (1975) Orthogonal polynomials, 4th edn. American Mathematical Society, Providence

    MATH  Google Scholar 

  60. Daubechies I (1992) Ten lectures on wavelets. SIAM, Philadelphia

    MATH  Google Scholar 

  61. Gupta AK, Ray SS (2015) Numerical treatment for investigation of squeezing unsteady nanofluid flow between two parallel plates. Powd Technol 279:282–289

    Google Scholar 

  62. Pandey AK, Kumar M (2018) Squeezing unsteady MHD Cu-water nanofluid flow between two parallel plates in porous medium with suction/injection. Comput Appl Math J 4(2):31–42

    Google Scholar 

  63. Singh K, Rawat SK, Kumar M (2016) Heat and mass transfer on squeezing unsteady MHD nanofluid flow between parallel plates with slip velocity effect. J Nanosci 2016:11

    Google Scholar 

  64. Domairry G, Hatami M (2014) Squeezing Cu–water nanofluid flow analysis between parallel plates by DTM-Padé Method. J Mol Liq 193:37–44

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Arts and Sciences, Department of Mathematics, Pamukkale University, 20100, Denizli, Turkey

    İbrahim Çelik

Authors
  1. İbrahim Çelik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to İbrahim Çelik.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Çelik, İ. Squeezing flow of nanofluids of Cu–water and kerosene between two parallel plates by Gegenbauer Wavelet Collocation method. Engineering with Computers 37, 251–264 (2021). https://doi.org/10.1007/s00366-019-00821-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-019-00821-1

Keywords

Search

Navigation