Object surface reconstruction from flow tracers

Abstract

A method to identify the surface of solid models immersed in fluid flows is devised that examines the spatial distribution of flow tracers. The fluid–solid interface is associated with the distance from the center of a circle to the centroid of the tracers ensemble captured within it. The theoretical foundation of the method is presented for 2D planar interfaces in the limit of a continuous tracer distribution. The discrete regime is analyzed, yielding the uncertainty of this estimator. Also the errors resulting from curved interfaces are discussed. The method's working principle is illustrated using synthetic data of a 2D cambered airfoil, showing that one of the limitations is the treatment of an object thinner than the search circle diameter. The method is readily adapted to 3D and applied to the 3D PTV data of the flow around a juncture. The surface is reconstructed within the expected uncertainty, and specific limitations, such as the smoothing of sharp edges is observed.

Graphic abstract

1 Introduction

Flow field measurements based on particle imaging techniques (Adrian and Westerweel 2011; Raffel et al. 2018) have advanced in the last decades in terms of spatiotemporal resolution and velocity measurement range matching the requirements of complex flows as encountered for industrial applications (Schanz et al. 2016; Discetti and Coletti 2018; Michaux et al. 2018, among others). Oftentimes, for aerodynamics studies, the attention is focused on the flow around an object immersed in a fluid stream. In selected cases, the velocimetry data are exploited to study the near-surface flow properties, such as pressure or even skin friction (Depardon et al. 2005; Ragni et al. 2009; Auteri et al. 2015; Jux et al. 2020, among others). For the latter task, accurate determination of the object surface position and orientation is deemed essential.

An overview of the literature returns a disproportionate comparison between methods dedicated to advance the analysis of the flow velocity and those that examine the geometry of the object immersed in the flow. As a result, the problem of object surface determination for applications in fluid flow investigations has only been studied in few works and problem-specific solutions have been proposed.

The imbalance is particularly evident in volumetric studies, where the diffuse illumination prevents the object identification by classical edge detection or masking approaches. The latter methods usually suffice in the 2D case, e.g., by tracing the characteristic sharp intensity gradient resulting from the light sheet striking the object. An overview of edge detection approaches is presented by Ziou and Tabbone (1998), including the well-known Sobel operator (e.g., Duda and Hart 1973) and the popular algorithm proposed by Canny (1986). Texton-based approaches, such as described in the work of Malik et al. (2001), are also well suited for the feature detection in 2D images. PIV-specific methods have been developed for the purpose of image filtering and mask generation. Examples thereof are the digital masking technique (e.g., Gui et al. 2003), the concept of anisotropic diffusion (e.g., Adatrao and Sciacchitano 2019), or the recently presented dynamic masking technique by Vennemann and Rösgen (2020) which relies on artificial neural networks. As indicated, these techniques work well in 2D PIV measurements, but they do not apply to surface reconstruction of generic 3D objects in fully volumetric flow investigations, which presents the main target of this work.

The advancement of three-dimensional PIV techniques (tomographic PIV, scanning light sheet techniques, digital defocusing, and PTV-based methods) is making the problem of object surface determination ever more relevant, with the need to characterize the flow properties around complex and three-dimensional objects (Discetti and Coletti 2018; Violato et al. 2011; David et al. 2012; Terra et al. 2020, among others).

The object geometry may be known a priori, e.g., by a computer-aided design (CAD) model, and determining a small number of reference points on its surface may sound a trivial solution. This approach, however, does not account for several sources of uncertainty: production and assembly tolerances, model deformations due to mechanical and aerodynamic loads or thermal stresses. The latter justifies the need for in-situ measurements of the fluid–solid interface.

The broader topic of interface detection (including fluid–fluid interfaces) within particle imaging techniques has been addressed from several perspectives: Adhikari and Longmire (2012) developed the visual hull method for tomographic particle image velocimetry (PIV) measurements around moving objects, which automates the process of identification and masking of the solid object, and thereby, suppresses the reconstruction of ghost particles inside the solid. Im et al. (2014) present the reconstruction of a refractively matched nasal cavity model, based on tomographic PIV measurements of the flow through the complex three-dimensional (3D) geometry. Also here, a key motivation in the latter study is the suppression of ghost particle reconstruction inside the solid object, ultimately improving the tomographic reconstruction quality in the fluid flow domain. Relevant work has been conducted in problems dealing with fluid interfaces: Reuther and Kähler (2018) evaluate detection methods for the turbulent/non-turbulent interface of wall-bounded flows through planar PIV measurements. Ebi and Clemens (2016) instead investigate the simultaneous measurement of a 3D flame front, and its encompassing velocity field by means of tomographic PIV.

This brief survey expresses the multifaceted nature of interface detection in particle imaging. Exception made for the visual hull method, an interesting commonality of the referenced studies above is that they attempt to discriminate a seeded phase where velocimetry measurements are taken, from a void region which is characterized by the absence of tracer particles.

Focusing on fluid–solid interfaces, an alternative approach to accurately determine the object surface is the introduction of an independent measurement system that detects markers distributed along the model geometry. Such dual measurements are typical for fluid–structure interaction (FSI) studies, which feature the fluid flow analysis, e.g., by PIV, combined with the study of the model's structural response, e.g., by digital image correlation (DIC). Two recent examples of such approach are presented by Zhang et al. (2019) on a flexible cantilever plate in a water current, and by Acher et al. (2019) who studied the deformation of a flexible wing with a synchronized DIC and tomographic PIV measurement. In some cases, the complexity of operating two separate systems may not be affordable, motivating the development of FSI methods in which the flow imaging system simultaneously captures the structural deformation. Such approaches typically rely on image separation strategies to distinguish between the flow tracers, and a marker pattern on the object surface. Examples include the works of Jeon and Sung (2012) and Im et al. (2015) on the flow around arbitrarily moving bodies, and the study of Mitrotta et al. (2019) on a flexible plate under gust loading. This type of approach, however, carries two disadvantages: (1) it may not be feasible in some conditions, e.g., when the model surface cannot be treated (consider the above case of the refractively matched model in the study of Im et al. (2014) for instance), and (2) it increases the information density on the imaging system, usually quantified in particles per pixel (ppp), which can hamper the achievable spatial resolution in the flow measurement. From these observations, stems the interest for interface detection approaches solely based on the fluid flow tracer measurements, as obtained by PIV techniques.

Lastly, it is noted that the studies of Im et al. (2014) and Ebi and Clemens (2016) utilize tomographic particle reconstructions followed by an analysis of the spatial particle distribution in a discretized (voxelized) domain. Similarly, the study of Reuther and Kähler (2018) includes methods that work on correlation-based PIV data as well as an approach that analyzes discrete pixel intensities in the 2D image. The advancements of particle reconstruction algorithms at high image source densities, such as the iterative particle reconstruction (IPR) method by Wieneke (2013) and the Lagrangian particle tracking algorithm "Shake-The-Box" (STB) by Schanz et al. (2016), have allowed to efficiently track individual particles at high spatial resolution. However, also within these latter cases, most research works have focused on the tracers motion analysis, leaving the problem of surface detection unexplored.

More recent applications of particle-based studies on complex geometries made with robotic volumetric PIV (Jux et al. 2018) have shown the critical role of accurate surface determination to map flow pressure and skin friction lines over a three-dimensional domain.

The present work addresses the problem of object surface detection making use of flow tracer analysis. The resulting method assumes therefore that the position of individual particle tracers flowing around an object can be detected in the three-dimensional space as done with existing particle tracking or reconstruction algorithms. Summarizing, the goal of the present study is to detect the surface of a solid object immersed in a seeded flow, solely based on the spatial distribution of flow tracers as recorded and reconstructed from a generic particle tracking velocimetry (PTV) measurement.

The working principle of the method investigated here follows the spatial distribution of particle tracers captured within a spherical neighborhood around the fluid–solid boundary, which separates the seeded and void region, respectively. The offset between the centroid of captured tracers and the geometrical center of the neighborhood provides the fundamental information for the measurement of the object surface position and orientation.

The working principle is discussed in the following section and illustrated for the 2D problem. A numerical illustration of the problem is presented with synthetically generated data around an airfoil (Sect. 3), before generalizing the developed theory to 3D space (Sect. 4). The interface detection method is assessed on an experimental data set capturing the 3D flow around a wall mounted obstacle in Sect. 5.

2 Principle of interface detection from flow tracers

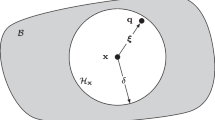
Let us consider the surface of a solid object immersed in a fluid flow where tracers are dispersed at random positions, up to the solid surface. The task of identifying the model interface translates into detecting the boundary between seeded and void regions. Figure 1 illustrates particle tracers randomly distributed above the flat surface of an object. When a circle of radius R is considered (a sphere will later be considered for the 3D analysis) at a distance h from the wall such that h > R, the distribution of particle tracers will feature a center of mass ξ close to the geometrical center of the circle (as in case of A). In the hypothesis of high tracer particle concentration c_p (corresponding to a small mean inter-particle distance λ_p), and a uniform particle distribution, the particles center of mass ξ coincides with the center of the bounding circle. When the circle approaches and partly intersects the wall (case B), the centroid of the particles distribution ξ is offset in a direction away from the wall, by a vector x_n from B. In more general terms we define x_n as the vector between the particles center of mass ξ and the search area's geometric center C_i:

$${\varvec{x}}_{n} = \xi - C_{i}$$

(1)

Fig. 1

Schematic 2D particle distribution near a fluid–solid interface (Γ_F-S)

In the specific condition where the circle is centered on the object surface (case C) the centroid offset reaches a specific value. The latter can be associated with the wall position detection. Furthermore, for a circle centered inside the solid (h < 0, case D), the distance |x_n| keeps increasing and tends to become the circle radius when the circle is fully immersed in the solid. In the latter case, the centroid of the particles distribution cannot be defined as no particle is captured inside the circle (h ≤ -R, case E). The analytical expression of the offset |x_n| as a function of h is derived and discussed in the remainder.

It can be concluded from the above analysis that the magnitude of the vector x_n spanned between the mean particle position ξ and the geometrical center C_i of the circular search area (SA) indicates whether C_i lies within the fluid domain or is part of the solid region. Moreover, the direction of x_n can provide an estimate of the normal to the surface.

In the following, $\left| {{\varvec{x}}_{n} } \right|$ denotes the centroid shift. The expected centroid shift can be expressed as a function of the elevation h (the wall-normal distance of C_i with respect to the object interface Γ_F-S). Modeling the fluid domain as a continuum, the centroid shift for any point C_i with elevation h smaller than the search radius R, follows from the geometric center of the search area's segment coinciding with the fluid domain (Ω_Fluid). A graphical definition of the key parameters is provided in Fig. 2.

Fig. 2

Illustration defining key parameters and terminology used in proposed interface detection concept. Search segment shaded in blue, bounded by the circle of radius R, around the assessment point C_i, located at a wall-normal distance h to the fluid–solid interface Γ_F-S. The centroid shift vector ${\varvec{x}}_{n}$ connects C_i with the geometric search-segment center ξ_c

An analytical expression of the centroid shift |x_n| as a function of the elevation from the surface h, maintaining a constant search radius R, is derived hereafter. The result is presented for the 2D problem and later generalized to 3D space. The validity of the expression is based on the following assumptions: 1) the particles concentration is modeled as a continuous distribution (limit of infinite concentration); 2) the surface is flat and aligned with x-axis. Upon these assumptions, it is trivial that the centroid position in wall-parallel direction (x) is located on the symmetry axis (x = 0), and only the wall-normal component (y) needs to be considered.

Defining a system of axes with origin at C_i, the centroid shift |x_n| is identical to the search segment's geometric center ξ_c. (The subscript c denotes the continuum representation.) The latter is determined through integration, following the definitions provided in Fig. 2,

$$\xi_{c} = \frac{{\int y f\left( y \right){\text{d}}y}}{{\int f\left( y \right){\text{d}}y }}$$

(2)

where f(y) describes the circular arc of radius R.

$$x = \pm f\left( y \right) = \pm \sqrt {R^{2} - y^{2} }$$

(3)

Since the distribution is symmetric over the y-axis, only positive values of x, respectively f(y), are considered here. Substituting Eq. (3) into Eq. (2) and solving the integral on the interval [−h, R] yield the analytical solution for the search-segment centroid ξ_c dependent on the elevation h,

$$\xi_{c} \left( h \right) = \frac{{\mathop \int \nolimits_{ - h}^{R} y f\left( y \right){\text{d}}y}}{{\mathop \int \nolimits_{ - h}^{R} f\left( y \right){\text{d}}y}} = \frac{{\left[ { - \frac{1}{3} \left( {R^{2} - y^{2} } \right)^{\frac{3}{2}} } \right]_{ - h}^{R} }}{{\left[ {\frac{1}{2}\left( {y \sqrt {R^{2} - y^{2} } + R^{2} \tan^{ - 1} \left( {\frac{y}{{\sqrt {R^{2} - y^{2} } }}} \right)} \right)} \right]_{ - h}^{R} }} = \frac{{\frac{1}{3}\left( {R^{2} - h^{2} } \right)^{\frac{3}{2}} }}{{\frac{1}{2}\left( {\frac{{R^{2} \pi }}{2} - \left( { - h\sqrt {R^{2} - h^{2} } + R^{2} \tan^{ - 1} \left( {\frac{ - h}{{\sqrt {R^{2} - h^{2} } }}} \right)} \right)} \right)}}$$

(4)

Despite the complexity of the resulting algebraic expression, the function ξ_c(h) decreases monotonically in the interval h = [−R, R]. In the following, starred labels (^*) are used to indicate normalization by the search radius R. Figure 3 displays the dependence of the centroid shift ξ^* upon wall elevation h^*.

Fig. 3

Analytical centroid shift magnitude $\xi_{c}^{*}$ as function of wall-normal distance h*. Starred labels (*) indicating normalization by search radius R

As expected, the centroid shift is zero when the search segment does not intersect the interface ($h^{*} \ge 1$). As the wall-normal distance reduces, the centroid shift gradually increases, reaching a critical value of $\xi_{crit}^{*} = \frac{4}{3\pi }$ at the interface (h^* = 0). For points inside the object (h^* < 0), the centroid shift keeps increasing up to a maximum value of 1, when h^* = -1. Based on this observation, we define a criterion to discriminate whether the point C_i belongs to the fluid or the solid region:

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left| {{\varvec{x}}_{n}^{\user2{*}} } \right| < \xi_{{{\text{crit}}}}^{*} \to C_{i} \in {\Omega }_{{{\text{Fluid}}}} } \\ {\left| {{\varvec{x}}_{n}^{\user2{*}} } \right| = \xi_{{{\text{crit}}}}^{*} \to C_{i} \in {\Gamma }_{{{\text{F}} - {\text{S}}}} { }} \\ \end{array} } \\ {\left| {{\varvec{x}}_{n}^{\user2{*}} } \right| > \xi_{{{\text{crit}}}}^{*} \to C_{i} \in {\Omega }_{{{\text{Fluid}}}} } \\ \end{array} } \right.$$

(5)

Additionally, we note that the centroid shift as function of wall elevation h^* as given in Eq. (4) and illustrated in Fig. 3 can be classified into three regions: (1) far away from the interface ($|h^{*} | > 1$), the centroid shift is zero, and thus, constant; (2) in close proximity to the interface (|h^*| ≲ 0.5), the centroid shift is well approximated by a linear trend, which is indicated by the tangent $(\frac{{{\text{d}}\xi_{c}^{*} }}{{{\text{d}}h^{*} }})$ at h^* = 0 shown in Fig. 3; and (3) for moderate wall elevations (0.5 ≲|h^*|≤ 1), the centroid shift is accurately described by Eq. (4) but it follows a nonlinear shape, as shown in Fig. 3.

2.1 Discrete problem formulation

When the hypothesis of a continuous distribution of tracers is removed, the effect of a finite number of tracers falling within the SA needs to be considered. The statistical analysis hereafter takes as key parameters the SA radius R and the tracers spatial concentration c_p. Assuming a tracer particles distribution that is approximately uniform within the local search area, the number N of particles within the circular SA is directly proportional to the area of SA coinciding with the fluid domain. The latter is equal to the denominator of Eqs. (2) and (4) and is graphically illustrated in Fig. 4.

Fig. 4

Relative share of search- and solid-segment area as function of normalized wall-normal distance h^*. The former is directly proportional to the expected ensemble size N for a given particle concentration c_p

Treating the tracer particle position as a discrete random variable, whose distribution is governed by the shape of the search segment, the expected mean position is identical to the continuum centroid (ξ_c, see Eqs. (2) and (4)) and the variance ($\sigma_{\xi }^{2}$) around the mean position can be estimated as,

$$\sigma_{\xi ,y}^{2} = \int y^{2} {\text{pdf}}\left( y \right)dy - \xi_{y}^{2} = \frac{{\mathop \int \nolimits_{ - h}^{R} y^{2} f\left( y \right)dy}}{{\mathop \int \nolimits_{ - h}^{R} f\left( y \right)dy }} - \xi_{c}^{2}$$

(6)

which is only shown for the wall-normal y-direction here, but can be analyzed in the equivalent manner for the wall-parallel x-direction. The expansion of the integral is omitted here, and only the resulting standard deviation ($\sigma_{\xi }^{*}$) as function of wall-normal distance h^* is shown in Fig. 5. Comparison of the standard deviation in the wall-normal ($\sigma_{\xi ,y}^{*}$) and the wall-parallel direction ($\sigma_{\xi ,x}^{*}$) suggests that the variability in the normal direction is significantly smaller, exception made for the limit cases (|h^*|= 1), which do not feature any directional sensitivity.

Fig. 5

Expected standard deviation in interface normal (y) and parallel (x) direction when modeling particle position as random variable inside a search segment defined by h^* and R

Figure 5 illustrates the expected variability for a single data point. For a distribution of N samples, the standard deviation of the mean instead scales with $N^{{ - \frac{1}{2}}}$ based on,

$$\sigma_{{\overline{\xi },i}}^{*} = \frac{{\sigma_{\xi ,i}^{*} }}{\sqrt N }$$

(7)

Upon this observation, the uncertainty for the centroid shift obtained from a discrete distribution of tracers can be estimated as function of the sample size. This is illustrated for a point coinciding with the fluid–solid interface (h^* = 0; $\sigma_{\xi , x}^{*} = 0.5$, $\sigma_{\xi ,y}^{*} \approx 0.26$) in Fig. 6. For the specific case of an interrogation point located on the fluid–solid interface (h^* = 0), the sample size is denoted by the variable k in the remainder.

Fig. 6

Expected standard deviation of mean particle position in interface normal (y) and parallel (x) direction as function of sample size when modeling particle position as random variable inside a semicircular search segment of radius R located at the interface (h^* = 0)

Based on this analysis, the necessary sample size k_min for a desired confidence and uncertainty level of the discretely calculated centroid shift $\left| {{\varvec{x}}_{n}^{\user2{*}} } \right|$ can be determined. In the assumption that the latter is dominated by the wall-normal component, the sample size selection can be based solely on $\sigma_{{\overline{\xi },y}}^{*}$. Furthermore, assuming a known tracer particle concentration c_p (in particles/m²), the minimum required search radius is given by,

$$R_{{{\text{min}}}} = \sqrt {\frac{{2k_{{{\text{min}}}} }}{{\pi c_{{\text{p}}} }}}$$

(8)

Similarly, the sample size can also be selected based on a desired directional accuracy of the interface normal estimate ${\varvec{x}}_{n}$. Let us define θ as the angle between ${\varvec{x}}_{n}$ and the wall normal y, with positive values indicating a counterclockwise rotation of ${\varvec{x}}_{n}$. Assuming the angle θ is dominated by the wall-parallel uncertainty $\sigma_{{\overline{\xi },x}}$, and further, that the small angle approximation can be applied ($\xi_{x} \ll \xi_{y} \cap \sigma_{{\overline{\xi },x}} \ll \xi_{y}$), the directional uncertainty for a coverage factor m is estimated as follows,

$$U_{\theta } \approx \frac{{m\sigma_{{\overline{\xi },x}}^{*} }}{{\xi_{{{\text{crit}}}}^{*} }}$$

(9)

Let us provide the following example as an illustration: Assume for a given tracer particle concentration c_p, a search radius R is selected such that for a semicircular search segment around a point C_i coinciding with the flat interface, k = 100 tracer particles are captured within the search area. Prescribing a 95% confidence interval (m = 2), the discrete centroid shift magnitude is expected to be accurate within 0.05R based on Eq. (7), whereas the directional accuracy shall be within 13.5° according to Eq. (9).

2.2 Methodical detection of a fluid–solid interface

Prior to application and assessment of the theory outlined up to this point, the above considerations are consolidated, providing a graphical illustration of the interface detection method on a flat interface. Considering a generic 2D tracer particle distribution of concentration c_p, as shown in Fig. 7a, the search radius R is chosen such that on average k = 30 particles are contained in a semicircular search segment spanned by R. To evaluate the distribution characteristics systematically, a uniform grid of assessment points C_i is defined, with a grid spacing of h_x = h_y = 0.5R in both axis directions. At each grid node, the centroid shift vector ${\varvec{x}}_{n}$ is evaluated based on the nearby tracers within the radius R, following Eq. (1). The resulting contour of the centroid shift magnitude $\left| {{\varvec{x}}_{n} } \right|$ is shown in Fig. 7b, normalized by the search radius R. The highlighted contour of $\left| {{\varvec{x}}_{n} } \right| = \xi_{crit} = \frac{4R}{{3\pi }}$ in Fig. 7b does therefore provide the estimate of the fluid–solid interface $\Gamma_{F - S}$ according to Eq. (5). Additionally, evaluating the direction of ${\varvec{x}}_{n}$ along the identified contour provides the estimate of the corresponding interface normal direction as shown in Fig. 7c. The individual steps taken in this analysis are summarized in a workflow diagram describing the proposed flow tracer-based interface detection algorithm in Fig. 7d.

Fig. 7

Schematic illustration of interface detection algorithm. a Tracer particle distribution on top of model surface with regular grid of assessment points. b Resulting centroid shift map, normalized by the search radius R. Iso-contour of critical displacement ξ_crit in red provides the reconstructed interface. c Estimation of the interface normal based on direction of ${\varvec{x}}_{n}$ along the identified contour. θ defines the angle between ${\varvec{x}}_{n}$ and the y-axis, with positive values indicating a counterclockwise rotation of ${\varvec{x}}_{n}$. d Workflow diagram of the proposed method

An element which has not been discussed yet is the grid-spacing parameter h_x, defining the distance between the assessment points C_i. Assuming the iso-contour of the critical displacement $\left| {{\varvec{x}}_{n} } \right| = \xi_{crit}$ is approximated by linear interpolation of the discretely evaluated centroid shift vector field x_n on C_i, results in the requirement that h_x must be sufficiently small, such that the change of $\left| {{\varvec{x}}_{n} } \right|$ across the interval h_x can be considered linear around the location of the interface. Reconsidering the analytically anticipated centroid shift as function of wall elevation h in Fig. 3, it was concluded that the assumption of linearity is a good approximation on the interval [−R/2, R/2] around the interface (h = 0), providing the condition that the grid spacing h_x shall be smaller than the search radius R.

If considering a regularization of the centroid shift map x_n on C_i, however, e.g., by linear regression, the assumption of linearity for x_n must hold on the full interval over which the regression is applied. Considering a kernel of 3 × 3 grid points C_i, the linearity assumption must hold across the kernel's diagonal, yielding the criterion that $2 \cdot \sqrt 2 h_{x} \le R$.

2.3 Surface curvature

The model developed up to this point assumes solely flat interfaces. As such, application of the proposed method to curved interfaces presents a source of error that is to be understood. To estimate the positional error associated with object curvature, let us consider an interface of constant curvature radius ρ. Further, let us distinguish between concave and convex interfaces, as illustrated in Fig. 8.

Fig. 8

Centroid shift analysis for concave (left) and convex (right) interfaces

For both, concave and convex interfaces, the search segment's centroid in the continuum assumption is obtained by superposition of the previously derived solution for the centroid of a circular segment (see, Sec. 2, Fig. 2, Eqs. (2–4)). To this end the search segment on the curved interface is split into two circular segments along the radical line of the search area of radius R and the curved interface of radius ρ as illustrated in Fig. 8. The elevation of the radical line (h') is defined by,

$$h^{\prime} = \frac{{l^{2} - \rho^{2} + R^{2} }}{2l}$$

(10)

where l indicates the position of the center of curvature with respect to the search area center C_i. With the origin defined at C_i, l therefore equals the y-coordinate of the center of curvature, $\rho - h$ and $- \left( {\rho + h} \right)$ for concave and convex case, respectively, as indicated in Fig. 8.

The centroid $\xi_{1}$ of the segment bounded by the radical line and the search radius R (blue, with dashed contour in Fig. 8) is found by adjusting the integration limits in Eq. (4) to [h', R]. The centroid $\xi_{2}$ of the segment bounded by the radical line and the interface (shaded in red) is determined in the equivalent manner: The search radius R is substituted by the curvature radius ρ. For the concave interface, the integration is carried out on the interval [l $+ h^{\prime}$, ρ], and the result is mapped by subtracting the integral from the distance l, to match the chosen reference frame with origin at C_i.

$$\xi_{2} \left( {h^{\prime}} \right) = l - \frac{{\mathop \int \nolimits_{{l + h^{\prime}}}^{\rho } y \sqrt {\rho^{2} - y^{2} } {\text{d}}y}}{{\mathop \int \nolimits_{{l + h^{\prime}}}^{\rho } \sqrt {\rho^{2} - y^{2} } {\text{d}}y}}$$

(11)

For the convex case, the integration limits are defined by [$\left| l \right| - h$', ρ] and the result is mapped by subtracting the magnitude |l| from the integral.

$$\xi_{2} \left( {h^{\prime}} \right) = \frac{{\mathop \int \nolimits_{{\left| l \right| - h^{\prime}}}^{\rho } y \sqrt {\rho^{2} - y^{2} } {\text{d}}y}}{{\mathop \int \nolimits_{{\left| l \right| - h^{\prime}}}^{\rho } \sqrt {\rho^{2} - y^{2} } {\text{d}}y}} - \left| l \right|$$

(12)

Lastly, the joint centroid is found by superposition,

$$\xi_{c} = \frac{{\sum \xi_{i} A_{i} }}{{\sum A_{i} }}$$

(13)

where A_i indicates the segment area. The resulting centroid estimate for selected curvature radii is plotted in Fig. 9 (left).

Fig. 9

Effect of surface curvature. (Left) Centroid estimate for selected curvature radii ρ. Negative values of ρ correspond to a convex surface. Dash–dotted line representing reference for a flat interface, with the dashed horizontal line indicating the corresponding critical centroid shift in the assumption of a flat interface. (Right) Resulting error in wall elevation when applying flat interface assumption for the critical centroid shift ξ_crit. Starred quantities indicating normalization by search radius R

As expected, the centroid shift is overestimated on concave interfaces, whereas a reduced shift is observed on convex shapes. Adhering to the flat interface assumption thus causes the reconstructed interface to be dilated on concave boundaries and to be eroding the true interface on convex shapes. Figure 9 (right) shows the anticipated positional error as function of curvature radius. It is concluded that the positional error of the detected interface is within 5% of R when the radius of curvature of the surface exceeds 4R. In principle, the data in Fig. 9 (right) can be used for a first-order correction of the interface reconstruction, after estimating its curvature profile. In this work, however, we do not consider such curvature correction.

To illustrate the working principle of the proposed concept and to discuss its main parameters, the method is applied to the synthetic particle distribution around a 2D airfoil hereafter.

3 Numerical illustration

The test object for the synthetic study presented in this section is the DU 91-W2-250 wind turbine dedicated airfoil shown in Fig. 10 (Timmer and van Rooij (2003)). Wind turbine blades are often deflecting substantially during operation and wind tunnel testing. The determination of the blade surface during wind tunnel experiments is thus of particular relevance.

Fig. 10

Airfoil shape (DU 91-W2-250, Timmer and van Rooij (2003)) immersed in random particle distribution at the coarsest considered tracer concentration ($\lambda_{p} = 0.01$ c)

The thick and cambered airfoil features a wide range of curvature radii, along with a pointy trailing edge. Applying the curvature analysis from Sect. 2.3 to the specific geometry indicates the reconstruction error that is to be anticipated for a given search radius R, as illustrated in Fig. 11. It is evident that regions of high curvature, such as the airfoil leading edge, present a specific challenge for reconstruction by the proposed algorithm.

Fig. 11

Airfoil model with contour colored by curvature (blue/convex—white/neutral—red/concave), and expected reconstructed shape (dashed black) following error analysis in Sect. 2.3 based on a continuous distribution and assuming a search radius of R = 0.1c as indicated in the top right, with c being the airfoil chord

Key parameters in the interface detection routine are investigated. First, the influence of the sample size—that is, the number of tracers used for calculation of the centroid shift vector—is evaluated (Sect. 3.1), which connects to the previous discussion on expected uncertainties in the discrete centroid estimate. Note that the particle count is expected to vary due to the random nature of the tracer distribution, and a reduction in the search-segment area for circles intersecting the solid object. Thus, specifications of the sample size k in the following refer to the mean number of particles expected in a semicircular search segment centered at a flat fluid–solid interface, in line with the definition provided in Sect. 2.1. The effect of tracer particle concentration is addressed separately in Sect. 3.2. Lastly, Sect. 3.3 incorporates the application of a regression model to the discretely evaluated centroid shift data.

The quality of the reconstructed interface is quantified in terms of positional accuracy only, which is reported by the maximum and root mean square distance of the reconstructed contour normal to the reference geometry, $\epsilon_{{x_{{{\text{max}}}} }}$ and $\epsilon_{{x_{{{\text{rms}}}} }}$, respectively.

3.1 Sample size

Focusing on method-specific parameters, the sample size is controlled by specification of the search radius R for a known concentration c_p, respectively, mean nearest neighbor distance $\lambda_{p}$. Mean particle distance and concentration in 2D are related as follows (Bansal and Ardell (1972)),

$$\lambda_{{\text{p}}} = \frac{1}{{2\sqrt {c_{{\text{p}}} } }}$$

(14)

In the analysis of the sample size, we limit ourselves to two seeding levels: a coarse tracer distribution ($\lambda_{{\text{p}}} = 0.01c)$ which is considered representative of an instantaneous particle image analysis, and a dense case ($\lambda_{{\text{p}}} = 0.001c$) equivalent to the study of multiple (here, 100) particle images acquired on a steady model. The airfoil chord length c is used to normalize $\lambda_{p}$ for the specific case of the 2D airfoil. In the following, different search radii R are considered, such that the expected average sample size in a semicircular search segment at a linear interface varies between 4 and 50 particles, based on Eq. (8). Figure 12 shows the corresponding positional reconstruction error as function of sample size.

Fig. 12

Maximum and mean positional error of reconstructed airfoil contour, as function of mean sample size k. Note the scale difference for the y-axes, between the coarse data ($\lambda_{p} = 0.01 c$) corresponding to the left axis, and the high-resolution data ($\lambda_{p} = 0.001 c$) on the right axis. Data show averaged error from 100 independent synthetic particle distributions

The data in Fig. 12 suggest that two types of error can occur in the reconstruction of the airfoil shape: For low values of k (< 10) a steep increase in the positional error is observed. For such small sample sizes, a high uncertainty in the centroid estimate is to be expected (see Sect. 2.1, Eq. 7), which can lead to false interface detection and consequently, large positional errors. Opting for larger sample sizes, the search radius R increases, which limits the spatial resolution of the reconstruction. As such, a gradual error growth is observed for large values of k (> 20), in particular in the maximum positional error. In this regime, comparison of the maximum positional error and the search radius R indicates a direct correlation between the quantities.

This trend is understood by inspection of a specific case. Figure 13a details the centroid shift magnitude for the coarse case ($\lambda_{{\text{p}}} = 0.01c$), normalized by the critical centroid shift ξ_crit, at a mean sample size of k = 30 (R = 0.09c) along with the resulting interface upon identification of the unity contour in Fig. 13b. The corresponding positional error is shown in Fig. 13c. While the centroid shift magnitude in Fig. 13a indicates a clear increase towards the airfoil model, four peculiarities are observed:

• 1. Far inside the model (|h|> R), the centroid shift cannot be computed as no tracer particles are available here.

• 2. The thin aft section does not cause a significant increase in the centroid shift magnitude. The airfoil thickness in this section is smaller than the search segment's radius. In such case, search segments in model vicinity capture tracer particles on either side of the model, resulting in a reduced distribution bias. This yields the observed reduction of the centroid shift magnitude, which ultimately results in an eroded interface contour when adhering to the assumption of a flat and infinitely thick solid object.

• 3. Along the aft airfoil section, at around x/c = 0.7, the reconstruction of a secondary interface inside the object is seen. Here, the object thickness is between the search radius and the search diameter. Under this circumstance, approaching the model from either side the centroid shift is expected to behave as demonstrated for the hypothesized flat and infinitely thick solid in Sect. 2. Yet, for assessment points penetrating the model surface the centroid shift magnitude is expected to shrink back to zero again towards the center of the thick object. In such case, two additional occurrences of the critical centroid shift magnitude must be anticipated, both of which are identified as the presence of a fluid–solid interface despite being located inside the solid. These errors associated with the finite model thickness justify the observation that the maximum error in Fig. 12 correlates well with the search radius R, in the assumption that the error due to model thickness is dominant. It further provides a motivation to keep the sample size k low, for minimization of the positional error.

• 4. Around the airfoil leading edge, a delayed increase in the centroid shift magnitude is seen. The leading edge geometry is characterized by high curvature (small radius of curvature), violating the assumption of a flat (non-curved) interface. This yields an erosion of the convex, curved leading edge, as shown in Fig. 13b, and the increased (negative) error magnitude in Fig. 13c. Such behavior has been foreseen in the discussion in Sect. 2.3.

Fig. 13

Application of the proposed method to the synthetic 2D particle distribution around an airfoil of chord c, with mean inter particle distance $\lambda_{p} =$ 0.01c. a Centroid shift map with airfoil silhouette indicated by solid black line and reconstructed interface by dashed black contour. b Reconstructed interface (blue) with anticipated error band based on 95% confidence interval using Eq. (7). Magenta contour illustrating expected reconstruction accounting for curvature effects. Dashed lines above and below camber line highlighting where model thickness is beyond the search radius R. The search area size is illustrated on the bottom right by a light blue circle. c Reconstruction error in terms of wall-normal distance, separated for pressure and suction side, and normalized by airfoil chord c

The analysis of the synthetic distribution examined here indicates that two error types must be considered in the selection of the sample size k: If the sample size is too small, high uncertainties in the centroid estimate negatively affect the surface reconstruction. Large values of k instead yield a loss in resolution, which amplifies the bias errors on curved surfaces and limits the detection of features smaller than search diameter. For the particular case studied here, error minimization is achieved for a mean sample size of 10 ≤ k ≤ 20 tracers captured inside a semicircle of search radius R, depending on the particle concentration.

3.2 Tracer concentration

The sample size assessment indicated that the reconstruction error is dominated by the search radius R. The latter can be reduced for the same sample size, if the tracer particle concentration is high, respectively, the mean particle distance is low. In an instantaneous measurement, it is likely that the achievable tracer concentration will dictate the positional error of the interface reconstruction. In a time-averaged study, an abundance of tracers can slow down the particle analysis, however. In such case, data subsampling to a concentration level that allows for surface reconstruction at a desired positional accuracy is preferable. To this end, the mean particle distance around the airfoil is successively reduced, keeping the mean sample size constant at k = 50. The resulting trend is illustrated in Fig. 14. For the range of mean particle distances considered here, the mean and maximum positional error reduces approximately linearly with mean particle distance.

Fig. 14

Maximum and mean positional error in airfoil reconstruction with change in tracer particle concentration. Error data averaged from 100 independent synthetic particle distributions

3.3 Data regression

The centroid shift contours shown in Figs. 7b & 13a indicate how |x_n| can vary even away from the interface. Such fluctuations are due to the random particle distribution. The reduction in such noise can be achieved by increasing the sample size. For a given particle concentration c_p, the sample size can only be raised by increasing the search area, and thus the search radius R. The latter limits the achievable resolution, which is undesirable following the previous analysis in Sect. 3.1. Instead, data regularization is realized by regression of the centroid shift field. Recalling the centroid shift as function of wall elevation in the continuum assumption (see Fig. 3), the relation is approximately linear with h, motivating the application of a linear regression model.

$$\overline{\user2{x}}_{n} = a_{1} x + a_{2} y + a_{3}$$

(15)

Such regression is applied on a sliding kernel to regularize the centroid shift contour. Because the centroid shift as a function of the wall distance is expected to be linear only within a domain of ${\Delta }h \le R$, the kernel width should be smaller than the search radius to avoid truncation. Herein, we consider a 5 × 5 kernel surrounding a grid point C_i on a structured grid of grid spacing h_x = 0.2R. The resulting centroid shift contour is shown and compared to the original map for one case in Fig. 15, whereas a comparison of the positional error is provided in Fig. 16 for varying particle concentration.

Fig. 15

Comparison of direct interface evaluation against evaluation after linear regression of the centroid shift field. a Original centroid shift field with unity contour in dashed black indicating identified interface. b Linearly regressed centroid shift field, using a sliding kernel of 5 × 5 points. c Comparison of reconstructed profiles for direct evaluation (blue) and regressed data (red), along with anticipated shape from curvature analysis (dashed-cyan). d Corresponding positional errors, separated for pressure and suction side

Fig. 16

Maximum and mean positional error with and without regression of centroid shift field. Linear regression on 5 × 5 kernel, with grid spacing of 0.2R. Data averaged from 100 synthetic particle distributions

Comparison of the reconstructed interfaces with and without regression in Fig. 15 shows the noise reduction effect of the data regularization. For the main airfoil body the regression-based interface follows the true profile more closely, and the construction of a secondary interface on the thin airfoil tail is avoided. Yet, the erosion of the curved leading edge as well as the truncation of the thin aft section is amplified on the regressed data. On average, the positional accuracy of the reconstructed interface is improved, as shown in Fig. 16, where both maximum and mean positional error are approx. 25% reduced when regression is applied.

This concludes the study on the synthetic particle distribution surrounding a cambered airfoil in a 2D plane. The study shows that the search radius must satisfy a balance, such that it includes a statistically significant number of samples, yet remains sufficiently small to maintain positional accuracy. For the specific case considered in Sect. 3.1 error minimization is achieved for 10 ≤ k ≤ 20, depending on the tracer particle concentration. In applications where the particle concentration is varying significantly across the measurement domain, this can motivate the implementation of a variable search radius approach, which is not considered in this work, however. The thin airfoil tail highlights that finite geometry effects must be considered when the search diameter is below the feature thickness of the investigated object. More accurate reconstructions can be obtained when the particle concentration is high, respectively, the average inter-particle distance λ_p is low. For the specific data considered here, the maximum reconstruction error is approximately one order of magnitude larger than the average inter-particle distance λ_p. Furthermore, a regularization of the centroid shift field is seen to smooth the interface reconstruction, which helps mitigating random fluctuations, but can amplify smoothing of curved and thin features.

4 Extension to 3D

The interface detection principle has been demonstrated for the 2D problem. For the 3D case, the circular search area for assessment of the local particle distribution changes to a spherical search volume, still bounded by the search radius R. This change affects the distribution characteristics analyzed for the 2D case in Sec. 2. Two key points are revisited for the volumetric case: the centroid shift as function of wall-normal distance in the continuum limit and the expected variability of the mean position for a discrete distribution.

Considering a planar interface, and modeling the fluid domain as a continuum the centroid shift x_n as function of wall elevation h is derived in the same way as for the 2D case. Only the distribution function f(y) (Eq. 3) changes to,

$$f\left( z \right) = \pi \left( {R^{2} - z^{2} } \right)$$

for the spherical case, which describes the cross-sectional area of a sphere at an elevation z normal to the interface. The search-segment centroid is then given by,

$$\xi_{c} = \frac{{\mathop \int \nolimits_{ - h}^{R} z f\left( z \right){\text{d}}z}}{{\mathop \int \nolimits_{ - h}^{R} f\left( z \right){\text{d}}z}} = \frac{{\pi \left[ {\frac{{R^{2} z^{2} }}{2} - \frac{{z^{4} }}{4}} \right]_{ - h}^{R} }}{{\pi \left[ {R^{2} z - \frac{{z^{3} }}{3}} \right]_{ - h}^{R} }} = \frac{{\frac{1}{4}\left( {R^{4} - 2R^{2} h^{2} + h^{4} } \right)}}{{\frac{1}{3}\left( {2R^{3} - h^{3} + 3R^{2} h} \right)}}$$

The critical centroid displacement at zero elevation is consequently equal to,

$$\xi_{{{\text{crit}}}} = \frac{3R}{8}$$

The centroid displacement is graphically illustrated as function of wall elevation in Fig. 17.

Fig. 17

Centroid shift magnitude as function of wall elevation h*, assuming a continuous fluid domain along a planar interface for circular and spherical search areas (volumes) in 2D and 3D, respectively

To predict the uncertainty of the mean particle position resulting from a discrete tracer particle distribution, the variance is evaluated for the limit case of zero elevation (h = 0, hemispherical search volume), similar to the 2D case (see, Eq. 6). As for the 2D case, in the volumetric study the variability parallel to the interface ($\sigma_{\xi ,x}^{*} = \sigma_{\xi ,y}^{*} = 5^{{ - \frac{1}{2}}} \approx 0.45$) is significantly larger as compared to the wall-normal direction $\sigma_{\xi ,z}^{*} = \left( {\frac{19}{{320}}} \right)^{\frac{1}{2}} \approx 0.24$, whereas the magnitudes are similar for planar and volumetric situation. Therefore, for both cases uncertainties in the discretely computed centroid shift x_n behave similarly.

Specific scrutiny of curvature and finite geometry effects is not provided for the 3D case. The qualitative behavior is expected to be equivalent to the 2D case shown in Sect. 2.3. Instead the working principles and limitations are demonstrated on the particle distribution surrounding a surface mounted test object in the following section.

5 Experimental assessment

The test object studied here is a simplified car side-mirror model, consisting of a wall-mounted cylindrical profile of semicircular cross section (d = 2r = h = 10 cm), rounded off with a quarter sphere (d = 2r = 10 cm), as illustrated in Fig. 18. Following common PIV practice, the model is painted black to limit surface reflections in the particle images. The experiment is conducted in a low-speed, open-jet wind tunnel, featuring a 60 × 60 cm² exit cross section which is run at 12 m/s free-stream velocity.

Fig. 18

Illustration of experimental setup, with wall-mounted side-mirror model

Experiments are conducted by Robotic volumetric PIV (Jux et al. 2018), in which particle images are acquired by a coaxial volumetric velocimeter (CVV, Schneiders et al. 2018). 10,000 image quadruples of 640 × 452 px² are recorded at a rate of 858 Hz. Helium filled soap bubbles (HFSB, Scarano et al. 2015) serve as tracer particles which are supplied by a 0.5 × 1.0 m² seeding system located in the wind-tunnel settling chamber. Individual tracers are located and tracked in time by the Lagrangian particle tracking algorithm "Shake-The-Box" (STB, Schanz et al. 2016). On average, about 320 particles are reconstructed and tracked in each image (0.001 ppp). The measurement volume is approximately 16 L (l), resulting in an average particle concentration of 200 particles/cm³ for the data ensemble. In this condition, the proposed method can only be used for reconstruction of stationary objects, whereas the application to moving bodies demands a significantly higher instantaneous tracer particle concentration.

The CVV is positioned above, and to the left of the test object, capturing the planar, downstream face of the side-mirror model and most of the upstream-facing, curved, left-half of the model. Raw images as shown in Fig. 19 (left) are preprocessed with a high-pass frequency filter (Sciacchitano and Scarano 2014), removing the majority of background noise and model reflections, see Fig. 19 (right).

Fig. 19

Example of particle images. Triple exposure of raw particle image (left) and corresponding preprocessed image (right). Approximate cylinder location indicated by white contour

We note that some reflections, stemming from soap contamination on the model is unsteady in time and is not efficiently filtered, resulting in a small share of ghost particles reconstructed inside the model. It is, furthermore, observed that the particle concentration is non-uniform due to inhomogeneous HFSB seeding. Differences in local particle concentration are up to one order of magnitude, with the highest concentration exceeding 600 particles/cm³ (lower, upstream section) and the sparsest regions counting approx. 50 particles/cm³ (upper section, see Fig. 20c).

Fig. 20

Particle distribution around test model. Data normalized by object radius r. Top view (left), side view (center), and front view (right). Highlighted features: a limit of optical access, b local particle void, c stream-tube with reduced particle concentration, d illumination limit e ghost particles due to soap contamination on model surface, f local particle void

The particle distribution shown in Fig. 20 is analyzed using the proposed interface detection routine, including the regression of the centroid shift field on a 5 × 5 × 5 kernel, as discussed in Sect. 3.3. Three different search radii are considered, the smallest being 5 mm, respectively, 0.1r, an intermediate search radius of 10 mm (0.2r), and a coarse search radius of 15 mm (0.3r). The resulting contours are compared in three selected planes in Fig. 21. Additionally the positional accuracy of the 3D reconstruction is reported in a mean sense, by evaluation of the root mean square error on the 3D model.

Fig. 21.

2D contours of model reconstruction based on experimental data for three different search radii. The corresponding SAs are illustrated in the left figure

The contours in Fig. 21 confirm that the proposed method is able to recognize the fluid–solid interface, despite some limitations: While the reconstruction of the planar downstream face closely follows the reference model, sharp features are not represented accurately but are smoothed in the reconstruction. As such, the convex corner on the transition from the cylindrical section to the flat rearward face is eroded, whereas the concave edge on the wall intersection is dilated. The degree of smoothing increases with the search radius. Focusing on the upper, spherical section (z > 2r), the contours in Fig. 21 (center & right) suggest a light erosion in the interface reconstruction, with the contours lying inside the reference object. The degree of erosion again increases with the search radius. This is in line with the presented 2D curvature analysis in Sec. 2, considering that the ratio of surface curvature over search radius for the experimental case is as small as 3.33 for the largest search radius considered (respectively, 5 and 10 for the smaller search radii). For the reconstruction on the upstream-facing cylindrical section, it is seen that the detected interface is outside the reference geometry, which is against expectations from the 2D curvature analysis. Therefore, we attribute this mismatch to a lack of tracer particles close to the model in this region, which can also be seen in Fig. 20 (left). Lastly, addressing Fig. 21 (right) it is seen that the reconstruction on the bottom-left corner is off. The contour detected here corresponds to the limit of the measurement domain, rather than a fluid–solid interface which becomes clear upon inspection of Fig. 20d. Instead, the vertical face in Fig. 21 (right) shows a wavy reconstruction pattern around z = 1.2r. This error is understood upon inspection of the particle distribution in Fig. 20e, f: A number of ghost particles is located inside the object here, stemming from a soap reflection on the model (see Fig. 19—left). The presence of these particles causes a local erosion of the reconstructed interface. Just outside the model, there is a region of low particle concentration in the fluid domain however (see Fig. 20—f), which results in a local dilation of the reconstructed interface. In combination, the wavy reconstruction pattern in Fig. 21 (right) is obtained.

To quantify the mean error of the 3D reconstruction, we limit ourselves to the LHS model only (y < 0) and isolate the domain of the interface reconstruction where optical access was provided during the measurement. On this domain, the normal distance from each vertex of the reconstructed interface with respect to the reference model is evaluated, which is illustrated in a contour plot for the intermediate search radius in Fig. 22.

Fig. 22

Reconstructed fluid–solid interface for a search radius of 10 mm (0.2r) colored by positional reconstruction error, indicating normal distance of reconstruction to reference model. Only the colored part is considered in the quantitative error analysis

The contour plot in Fig. 22 confirms the systematic erosion (dilation) of convex (concave) edges, with the convex edge of the planar rearward face being eroded (blue contour) and the concave edge on the wall interface being dilated (orange/red contour). Furthermore, a hole is visible on the side of the model, caused by the ghost particles reconstructed inside the model. The cylindrical section features a positive error, which is believed to stem from a lack of tracer particles in this region, as discussed previously on the 2D contours in Fig. 21. Interestingly, also the planar rearward face features a systematic positive error, albeit smaller in magnitude. Lastly, the spherical section presents a negative error, corresponding to an erosion of the solid model.

The mean positional error is summarized in Table 1, considering three regions of analysis: First, the root mean square error for the full reconstruction is reported, referred to as ε_total. Second, the same error is computed, excluding the hole that is reconstructed due to the presence of ghost particles (ε_sub). Lastly, the error on the inner part of the planar rearward face is evaluated separately, thereby excluding effects of surface curvature. For this last analysis on the planar face, the mean ($\beta_{{{\text{rwd}}}}$) and standard deviation ($\sigma_{{{\text{rwd}}}}$) are reported, rather than the root mean square error, in order to distinguish systematic and random error contributions.

Table 1 Experimental error analysis

The mean error based on the full reconstruction (ε_total) does not vary significantly with spatial resolution, respectively, the search radius. Excluding the erroneous reconstruction due to ghost particle presence, the error is reduced by approximately a factor two, while additionally showing a clear trend that the error magnitude reduces as the spatial resolution increases. Analyzing solely the planar rearward face, a bias error of approx. 1 mm is identified.

A source of this bias error is recognized upon inspection of the tracer particles' concentration gradient in the wall-normal direction: The mean concentration obtained in thin slices of 0.5 mm thickness, parallel to the planar downstream interface is shown in Fig. 23. The data suggest that within 3 mm from the model surface, the concentration drops from about 300 particles/cm³ far from the model, to zero particles at the interface, possibly due to some tracers impacting at the model surface. Thus, the assumption of a uniform particle distribution is not satisfied close to the model interface. The observed gradient supports the positive bias error reported above, as the centroid shift magnitude |x_n| will be amplified for assessment points that are affected by the local concentration gradient.

Fig. 23

Tracer particle concentration downstream of the test model

Besides the observed bias, a random error ($\sigma_{{{\text{rwd}}}}$) is observed, that is on the order of half a millimeter. The magnitude of the random error on the planar rearward face corresponds well with the mean HFSB tracer particle diameter, which is expected to be around 0.5 mm (Scarano et al. 2015; Faleiros et al. 2018).

Considering the typical spatial resolution of velocity field measurements acquired by a CVV system as studied here, we find that the mean flow field is typically ensemble averaged in sub-volumes (bins) of the order of 1 cm³, yielding a vector spacing of approx. 5 mm if assuming cubical bins at 50% overlap (Schneiders et al. 2018; Kim et al. 2020; Saredi et al. 2020, among others). The positional reconstruction error observed in the analysis presented here is therefore within the expected vector pitch of the flow measurement, in particular when excluding the error due to ghost particle presence. The latter is to be avoided for a reliable interface reconstruction.

6 Conclusion

A method for detection of fluid–solid interfaces in PTV measurements around immersed objects is proposed. The analysis is solely based on the spatial distribution of particle tracers in the fluid domain, assuming the interface between the seeded fluid flow and the void solid region is a valid representation of the object silhouette. The local distribution characteristic is assessed in a search area (volume) of radius R. The theoretical background is developed for the 2D case on a planar interface, whereas the proposed principle is first illustrated on the synthetic particle distribution surrounding a cambered airfoil.

The airfoil case exposes two limitations of the proposed method: First, surface curvature is not accounted for, yielding an erosion of convex and a dilation of concave interfaces. Such error is significant when the radius of curvature is of the same order of magnitude as the search radius R. Second, thin objects present a challenge for reconstruction: Features with thickness between the search radius R and the search diameter (2R) cause the reconstruction of a secondary interface inside the object, whereas elements with a thickness smaller than the search radius R might not be identified at all. The latter justifies that the maximum reconstruction error in the airfoil case correlates with the search radius R. Therefore, R is to be minimized while maintaining a statistically significant sample size inside the search area (volume).

The method is subsequently adapted to the 3D case and applied to the experimental PTV data recorded by a coaxial volumetric velocimeter around a simplified car's side-mirror model mounted on a flat plate. The experimental assessment shows that the object shape is retrieved within the expected resolution of the surrounding flow measurement, if the absence of ghost particles inside the solid object can be guaranteed.