Abstract
The volumetric defocusing particle tracking velocimetry (DPTV) approach is applied to measure the flow in the sub-millimeter gap between the disks of a radially grooved open wet clutch. It is shown that DPTV is capable of determining the in-plane velocities with a spatial resolution of \(12\;\upmu \mathrm{m}\) along the optical axis, which is sufficient to capture the complex and small flow structures in the miniature clutch grooves. A Couette-like velocity profile is identified at sufficient distance from the grooves. Moreover, the evaluation of the volumetric flow information in the rotor-fixed frame of reference uncovers a vortical structure inside the groove, which resembles a cavity roller. This vortex is found to extend well into the gap, such that the gap flow is displaced towards the smooth stator wall. Hence, the wall shear stress at the stator significantly increases in the groove region by up to \(15\%\) as compared to the ideal linear velocity profile. Midway between the grooves, the wall shear stress is around \(4\%\) lower than the linear reference. Furthermore, significant amounts of positive radial fluxes are identified inside the groove of the rotor; their counterpart are negative fluxes in the smooth part of the gap. The interaction of the roller in the groove and the resulting manipulation of the velocity profile has a strong impact on the wall shear stress and therefore on the drag torque production. In summary, this DPTV study demonstrates the applicability of such particle imaging approaches to achieve new insights into physical mechanisms of sub-millimeter gap flow scenarios in technical applications. These results help to bring the design- and performance-optimization processes of such devices to a new level.
Graphic abstract

Similar content being viewed by others
1 Introduction
The continuously increasing urge for \(\hbox {CO}_{2}\) savings and the expectation of a constantly increasing range of electric drive concepts lead to the need for new ways of saving energy in the automotive industry. The idling behaviour of wet multi-plate clutches is one of the building blocks to meet this trend. The speed difference between drive and output, in combination with the presence of oil and the sub-millimeter spacing of the plates, lead to a high wall shear stress and therefore to a significant torque, the so-called drag torque. Its reduction can save considerable amounts of energy, which in turn might lead to a significant efficiency gain of the entire power train. Consequently, a reduction of this adverse drag torque motivated a variety of both numerical and experimental investigations of the flow in open wet clutches (see e.g. Iqbal et al. 2013b; Pahlovy et al. 2016; Neupert et al. 2018; Neupert and Bartel 2019).
The open wet clutch flow can be simplified to a rotor-stator configuration with a driven flow originating at the center of the stationary disk, as illustrated in Fig. 1. Influencing parameters on the flow pattern are the volumetric flow rate Q of the supplied flow, the self-adjusting gap height h between the rotor and the stator disk, the inner and the outer radius of the rotating disk, \(R_1\) and \(R_2\), the angular velocity \(\Omega\), and the drag torque \(T_s\), resulting from the speed difference between drive and output unit that is shearing the oil.
Scheme of an open clutch with the most important geometric parameters, the fluid properties, and the region of interest for the investigation. (Adapted from Leister et al. 2020)
The main characteristic of any open wet clutch is the so-called aeration of the gap between rotor and stator, which occurs at a characteristic angular velocity \(\Omega _{\mathrm {air}}\) for a given (constant) flow rate \(Q_{\text {const}}\).
Despite the partly complex interplay of involved parameters, the aeration onset and corresponding drag-torque drop typically occur in the range of \(500< \Omega _{\mathrm {air}} < 1500 \mathrm {\ rpm}\) (respectively \(52< \Omega _{\mathrm {air}} < 157 \mathrm {\ 1/s}\)) as indicated by Yuan et al. (2010), Iqbal et al. (2013a), Takagi et al. (2012) and Neupert et al. (2018), for instance. Below this critical point of operation, the drag torque effectively scales linearly with the angular speed. Beyond this critical value \(\Omega > \Omega _{\mathrm {air}}\), ambient air is sucked into the gap due to the increasing influence of centrifugal forces, leading to a significant and rapid drop of the drag torque. Thus, the manipulation of the aeration onset to slower angular velocities is one of the major drag torque minimization strategies. This minimization is mainly achieved by means of surface grooves in the rotor disc. Unfortunately, the choice of geometry parameters for the grooves mostly relies on experience, which renders the scaling of the involved parameters particularly difficult. A step towards the predictability of the aeration point has been recently proposed by Leister et al. (2020) on the grounds of dimensionless (thus scalable) quantities. Up to now no velocity information is involved in the designing process of open wet clutches. However this information would enable a more precise development strategy to lead to a more efficient drive train. To date, mostly integral torque measurements, as described e.g. by Neupert et al. (2018), are used for designing clutches, not taking the actual flow physics into account. However, there is a lack of knowledge of clutch flows, since detailed flow information is challenging to retrieve from such devices. One step towards this desired velocity information has been made by Kriegseis et al. (2016), who combined particle image velocimetry (PIV) and laser Doppler velocimetry (LDV) to capture the flow in a grooved sub-millimeter rotor-stator gap of a generic open wet clutch. These phase-locked flow measurements successfully revealed the groove-pattern foot print. Due to the inherent limitations of the planar PIV measurements, only axially averaged velocity fields have been extracted from the raw data. For the determination of the local drag torque, however, the actual distribution of the velocity along the gap height is of utmost importance.
In continuation of this earlier investigation by Kriegseis et al. (2016), the present work focuses on resolving the flow field within the rotor-stator gap in all spatial dimensions. This requires a volumetric flow measurement technique, since the typical light sheet thicknesses are larger than the sub-millimeter clutch gap height. Moreover, the confined clutch geometry does not allow for employing multiple views of the measurement domain due to the limited optical access—a fact that effectively excludes multi-camera particle imaging techniques for capturing the flow in this application. As an additional hurdle, it is not possible to place a calibration target within the domain, since this requires a complete disassembly of the clutch model.
These drawbacks were recently addressed by Fuchs et al. (2016b), who successfully demonstrated that a single camera DPTV technique has the ability to resolve the flow velocity distribution along the optical axis in the range of a few millimeters with sufficient resolution. For inaccessible and confined measurement domains, the DPTV approach can be combined with an in situ calibration scheme, as shown by Fuchs et al. (2016a). The in situ calibrated DPTV approach also serves as the basis for this open wet clutch flow investigation. First, the principle of DPTV will be briefly recapped, followed by a detailed description of the experimental set-up. The results section comprises the comparison of two different approaches to deduce the defocusing information from the particle images, determining the particle location along the optical axis. The second part of the results section outlines the fluid mechanical findings as derived from the 3D3C velocity information, and finally their impact on clutch-operation strategies.
2 Experimental approach
2.1 Defocusing particle tracking velocimetry (DPTV)
Defocusing information of the particle images allows for the determination of the spatial particle location along the optical axis, a principle that has long been practiced in particle imaging since its introduction by Willert and Gharib (1992). DPTV is a straightforward technique that only requires a simple planar PIV equipment to determine the volumetric flow field. While Defocusing PTV is not a standard technique—there is no commercial software available—it is a powerful method for applications where planar PIV is not suitable. Whenever it is necessary to resolve flow structures with dimensions on the order of the light sheet thickness or even smaller, it is necessary to conduct three-dimensional (3D) flow velocimetry. Naturally, multi-camera approaches, such as 3D-PTV (Nishino et al. 1989) and tomographic PIV (Elsinga et al. 2006), are employed in such cases, since these are well-established and assessed techniques. However, when it comes to technical applications, the geometries of the domains can become more complex, vibrations can occur, and the accessibility of the measurement area may be limited. Such challenging measurement environments might leave the DPTV approach as the only remaining option to derive reliable velocity information at all.
The particle location along the optical axis, i.e. the z coordinate, is coded in the geometry of the particle image, more specifically in the diameter. Closer to the focal plane the particle image diameter becomes smaller, whereas if the particle is located further away from the focal plane, the particle image diameter increases, as illustrated in Fig. 2. In x and y direction the particle location is determined by the sensor location of the particle image center, provided that the scaling function does not change along z. For macroscopic objective lenses and small measurement depths as well as for micro objective lenses this is a valid assumption; for macroscopic experiments at larger measurement depths the particle x and y location becomes a function of the sensor location and the particle z location, or the particle image geometry, respectively, as outlined by Fuchs et al. (2014).
Principle sketch of defocusing particle imaging: depending on the location of the particle along the optical axis, the corresponding particle image has a distinct diameter. Here, the orange particle is closer to the focal plane, yielding a relatively small particle image diameter. For a particle further away from the focal plane, the particle image diameter increases, as indicated by the green particle
Olsen and Adrian (2000) derived a mathematical description of the defocusing function under absence of optical aberration effects, which quantifies the particle image diameter \(d_{i}\) in relation to the distance of the particle with the physical size (diameter) \(d_{p}\) to the focal plane as
The first term describes the geometric image with the magnification M. The second term exists due to the diffraction of light on the aperture of the camera, where \(\lambda\) appears as wave length of the light and \(f_{\#}\) is the focal number of the objective lens. The factor of 5.95 is related to the first minimum of the Bessel function of the first kind, which is considered to model the intensity of the diffraction.
The third term is the relevant one for the defocusing, and describes the diameter change on the image plane due to the distance \(z^*\) of the particle to the focal plane, where \(s_0\) additionally appears as the distance between the lens and the focal plane in the denominator. According to Olsen and Adrian (2000), \(s_0 \gg z^*\) applies for any optical set-up such that the image diameter change can be approximated by
When imaging the particles with sufficient distance \(\Delta z\) from the focal plane, the hyperbola can be approximated as a linear curve (see Fuchs et al. 2016a), where the third term of the equation dominates. The particles used in the present study have a mean diameter of \(d_{\mathrm {p}}=9.84 \; \upmu \mathrm{m}\) and a standard deviation of the diameter of \(\sigma =0.26 \; \upmu \mathrm{m}\). Figure 3 shows \(d_{\mathrm {i}}\) in pixel on the sensor chip calculated according to Eq. (1). The gray lines visualise the uncertainty of the diameter, as \(3 \sigma\)-deviation. It can be concluded from the narrow margin between the lines, that the influence of the physical particle-size deviation and its variation along the z location have no significant influence on the image diameter estimation for reasonable distance to the focal plane. In practice, the focal plane is located outside of the measurement volume in the direction closer to the camera to ensure sufficient accuracy for the approximated linear relation between the particle image diameter and the particle \(z^*\) location and furthermore to eliminate any influences of the particle diameter.
Visualisation of Eq. (1) for the input parameters of the present particle imaging approach. The red curve shows the image diameter \(d_i\) of the mean particle diameter as function of \(z^*\). Physical particle-size deviations are emphasized as a dark gray \(3\sigma\) margin. This margin vanishes for reasonable distance to the focal plane
Equation (1) does not take optical aberrations into account, which renders a direct application of this function for particle-location estimations impossible. For objective lenses with large magnifications, in particular, spherical aberrations have a strong influence on the defocusing function. One means to determine this function is the use of pinhole matrices that are imaged at distinct z positions along the measurement domain, since the pinhole images form the same diffraction pattern as particles of the same diameter (Babinet’s principle). In the present clutch-flow application it is not feasible to place a calibration target within the domain. Instead, the defocusing function is derived from the displacements of the recorded particle images, where the particle image diameters at the upper and lower boundary of the measurement volume are estimated on the grounds of the no-slip condition. Since the particle image diameter is considered to change linearly with the particle z location within the volume boundaries (see above), the particle location relative to the gap height can be immediately scaled using the known height h of the bounded measurement volume. This yields a simple linear relation between the particle z location and its particle image diameter d:
where m is the slope of the defocusing function. A more detailed description of the in situ calibration procedure—including methods on how to compensate a camera misalignment and field curvature—is outlined in Fuchs et al. (2016a).
The actual displacement of the particle images is determined by a simple nearest neighbour tracking algorithm, since the particle image density is fairly low due to the relatively large defocused particle images. Along with the sensor location X and Y of the particle image, the available diameter estimate is directly used for the third spatial location component, allowing for the connection of corresponding particle image pairs in 3D space.
2.2 Experimental procedure
All experiments were conducted at an open wet clutch facility, which provides optical access through the stator plate and a circumferential window in the clutch housing, see Fig. 4. The stator plate is made from anti-reflection coated float glass to ensure a high quality, low distortion optical access to the measurement domain. Its rotating counterpart can be exchanged to test different groove patterns or non-grooved rotor clutch plates. The clutch was operated at an angular velocity of \(\Omega =20.1\) 1/s with a constant moderate radial volumetric flow rate of \(1.0 \;\) l/min to ensure a single-phase flow. Repeatability of the experiments in terms of constant rotor speed and reasonably accurate phase resolution for the present case of a grooved rotor disk is ensured by an ADDA TFC 80A-2 motor in combination with a WL100L-F2231 optical sensor.
The clutch was operated with a white mineral oil (density \(\rho _o=850\) kg/m3, dyn. viscosity \(\mu =0.0136\) kg/ms at \(40^\circ C\), CAS No: 8042-47-5), which was seeded with fluorescent particles with a mean diameter of \(d_{\mathrm {p}}=9.84\,\upmu \mathrm{m}\) (density \(\rho _p=1510\) kg/m3, particle response time \(\tau _p=0.6\,\upmu \mathrm{s}\), emission wave length \(\lambda _e=584\) nm) to avoid reflections. The measurement volume was illuminated using an ILA_5150 light-sheet optics in front of a Quantel Evergreen Nd:YAG laser (\(\lambda =532\) nm, 70 mJ/pulse, pulse distance \(\Delta t=80\,\upmu \mathrm{s}\)). The particles were recorded in double-frame mode once per revolution, using an ILA.PIV.sCMOS camera (sensor size \(2560 \times 2160\) pixel, 16 bit) equipped with a Questar QM 100 long-distance microscope.
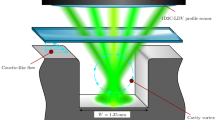
Note that the Defocusing PTV equipment is identical to a standard 2D planar PIV setup, where the only difference is the distinct offset between light sheet and focal plane. Here, the small focal depth of the Questar ensured a large defocusing sensitivity and in turn a good spatial resolution along the optical axis. As indicated in Fig. 5 phase-triggered experiments at two fields of view (FOV) have been conducted to compare the flow in the smooth part of the gap (FOV I) with the impact of a radially grooved cavity in the disk surface on the flow field (FOV II). A total number of 2000 image pairs was recorded for each FOV and magnification.
The optical set-up for FOV I and II has a magnification of \(M=7.0\) and a reproduction scale of \(0.92 \; \upmu \mathrm{m/pixel}\). This configuration provides a defocusing sensitivity of \(m=11.6 \; \upmu \mathrm{m/pixel}\), which corresponds to a 1 pixel diameter change of the particle image for a particle location change of 11.6 \(\upmu \mathrm{m}\) along the optical axis in z direction. Additionally, a smaller magnification of \(M=4.2\) with 1.55 \(\upmu \mathrm{m/pixel}\) reproduction scale and \(m=19.71\, \upmu \mathrm{m/pixel}\) defocusing sensitivity was used for FOV II to account for the larger depth of the measurement volume in the cavity and to provide a broader view on the cavity/gap interaction of the flow.
Starting from a diameter of around 50 pixel at the transparent stator wall, the chosen magnifications yield particle image diameter increases of around 30 and 50 pixel along the gap height of \(h=0.54\) mm for FOV I and FOV II, respectively. To avoid confusion, all upcoming diagrams provide information on the chosen magnification. The boundary conditions for the particle image diameter calibrations are (a) \({u_\varphi (z=0)=0}\) at the stator wall, (b1) \({u_\varphi (z=h)=\Omega r}\) at the smooth part the rotating disk (FOV I) and (b2)\({u_\varphi (z=h+H)=\Omega r}\) within the groove of the disk (FOV II).
The clutch facility was operated with a real industry-used rotor disk to ensure a realistic and meaningful test scenario. The inner and outer radii of the chosen disk are \(R_1=82.5\) mm and \(R_2=93.75\) mm, respectively. The 32 equidistantly distributed grooves lead to a groove-to-groove distance of 17.3 mm in circumferential direction at the mean disk radius \(R_{\mathrm {m}}\), where the latter also denotes the approximate center line of the chosen FOVs; see Fig. 5. The corresponding gap Reynolds number for the given quantities is \(Re_h=\Omega h^2/\nu = 0.36\) (see e.g. Lance and Rogers 1962, ), where \(\nu =\mu /\rho\) is the kinematic viscosity. Likewise, the lubrication Reynolds number for the given problem is \(Re_l=\Omega R_m h/\nu =59.7\), which is commonly used for tribology and (mixed) lubrication problems (cp. Tauviqirrahman et al. 2013; Gropper et al. 2016). According to Lance and Rogers (1962), a Couette-like velocity profile in circumferential direction can be expected in gaps of smooth rotor-stator configurations for gap Reynolds numbers \(Re_h<1\), which holds for FOV I of the present set-up. Note however, that even such low \(Re_h\) lead to slightly curved velocity profiles, which reveal increasing velocity gradients towards the rotor (Lance and Rogers 1962).
Figure 6 shows a detailed sketch of the radial groove geometry, also containing the origin of the coordinate system with the coordinates r, \(\varphi\), and z. In the present application the z direction also corresponds to the optical axis and represents the particle location along the gap height h with its origin \(z=0\) at the stator glass plate (cp. also Fig. 3). The radially oriented clutch grooves have a width of \(W=1.35\;\) mm in circumferential direction and a height of \(H=0.97\;\) mm in axial direction.
3 Results
3.1 Comparative particle image detection analysis
Deriving the spatial particle location from its particle image geometry is a crucial step for the single camera 3D DPTV velocimetry technique, since the uncertainty of the particle location estimation is directly connected to the accuracy of the particle image geometry determination. In microfluidics, where objective lenses with relatively large spherical aberrations are used, the auto-correlation function, defining the particle image boundary by a fixed correlation value, has shown to yield the best results for the geometry determination, as proven by Cierpka et al. (2010). The latter study showed that a Gaussian fit is not suitable to determine the particle image geometry, since the particle image intensity distribution is not Gaussian-like, even though the peak intensity is still in the center of the particle image. Another micro imaging approach to determine the particle image dimensions was outlined by Barnkob et al. (2015), where the particle images are cross-correlated with a set of reference images, recorded at well-known positions along the optical axis, to estimate their spatial location.
However, the significance of spherical aberrations is not as pronounced for macroscopic imaging, since the deviation from the ideal spherical wave front of a point source of light due to the aberration becomes small. As a consequence, the peak intensities of the particle images are not located in the center anymore. Instead the highest intensity appears at the outer rim of the particle image, which was first employed by Wu et al. (2005) to estimate the particle image diameter. Analogously, Fuchs et al. (2014) determined the particle image geometry by analysing the intensity distribution at its edges, where a fixed intensity value denoted the edge location. This method was later refined for the in situ calibrated defocusing approach, where a normalized intensity value, accounting for local intensity variations and noise, defined the particle image edge (see Fuchs et al. 2016a).
The optical set-up used in this investigation can be categorized between the microscopic and macroscopic set-ups that were introduced in the previous paragraphs. Figure 7 clearly illustrates that the highest intensity of the particle images is at their outer diffraction ring, while compared to the investigation of Fuchs et al. (2016a) the outer ring spreads over several pixels rather than forming a sharp edge; note that the intensity is inverted in the figure. To account for this particle image appearance during geometry determination, Leister and Kriegseis (2019) successfully demonstrated the application of the Hough transform (Hough 1959), which is an efficient method to detect circular shapes.
The remainder of this section addresses the comparison of the algorithms of Leister and Kriegseis (2019) and Fuchs et al. (2016a), where the latter has so far only been employed for a generic lab experiment and remains yet to be testified in more realistic and complex technical applications. From here on, the approaches will be referred to as circle detection (Leister and Kriegseis 2019) and edge detection (Fuchs et al. 2016a) approach, and will be compared in terms of their performance (i.e. the amount and local distribution of detected particle images), peak locking effects, and the uncertainty of the particle image geometry determination.
The total number of detected particle pairs in FOV I is 12,860 for the circle detection method and 14,718 the edge detection approach. The estimated particle image diameters and particle image displacements are shown in Fig. 8. The detected particle image diameters are indicated in Fig. 8a for three particle images at different locations z in the gap. Obviously, the circle detection identifies the intensity maximum as the characteristic diameter of the ring-type pattern, whereas the edge detection considers the outer rim of the bright pattern for the diameter determinations. This systematic difference leads to correspondingly two different slopes for the respective diameter/displacement transfer functions of the Couette-like flow in FOV I as plotted in Fig. 8b, which accordingly reveals a steeper slope for the edge detection algorithm.
Therefore, the particle displacement rather than the image diameter is considered for the direct comparison of detection occurrences along the gap as shown in Fig. 8c. Both histograms show decreasing detection rates for increasing particle displacements, where a sudden steeper drop in detection rate for the circle detection is salient for the largest particle displacements. Recall that zero displacement occurs at the stator wall, which is closer to the focal plane. As such, the negative slope of the detection rate can be attributed to the decreasing signal to noise ratio (SNR) of the particle images, since the light intensity emitted by the particle spreads over a larger sensor area, i.e. more pixels. The histograms consequently indicate similar performances of either approach for small and moderate image diameters but also reveals that the circle detection approach requires a higher SNR as compared to the edge detection approach.
The most important uncertainty quantity for DPTV is the accuracy of the particle image diameter determination, denoting the particle location in z direction. One means to approach the diameter determination uncertainty is the evaluation of the estimated particle image diameter change between the double frames.
The undisturbed gap flow above the smooth parts of the disk only propagates in circumferential and radial directions. Thus, in case of FOV I the flow in z direction is expected to be zero and so is the change of the particle image diameter. However, between the two frames, the diameter of a particle image does change due to the uncertainty of the diameter determination, which among others can be influenced by parameters such as the inhomogeneity of the illumination, the image noise, and the signal to noise ratio (SNR) of the particle images. Therefore, the standard deviation of all estimated diameter changes is calculated yielding the following values:
The circle detection approach leads to a particle image diameter determination uncertainty of \(2\sigma =2.39\;\) pixel.The edge detection method yields an uncertainty of \(2\sigma =0.97\) pixel, lying in the same range as compared to the macroscopic optical set-ups of Fuchs et al. (2016a, 2016b), where values in the range of \(2\sigma =0.79-1.03\;\) pixel were reported for the diameter determination uncertainty. This provides evidence that the comprehensive uncertainty assessments of DPTV that were presented in those publications also apply for this clutch flow experiment. To convert this particle image diameter determination uncertainty into a measure of the achievable resolution in z direction for the present clutch flow experiment, the \(2\sigma\) particle image diameter uncertainty is multiplied with the slope of the defocusing function, \(12.88\; \upmu \mathrm{m/pixel}\).
The resulting localization uncertainty of a particle along the optical axis then yields \(2\sigma _{z}=12.5\; \upmu \mathrm{m}\), which corresponds to a relative uncertainty of 2.3% at \(h=0.54\) mm measurement volume depth. Even though this number indicates that the flow within the gap can be well resolved despite the strong velocity gradients it has to be emphasized that \(\sigma _{z}\) directly affects the derived velocity estimate w in z direction. Translated into a velocity uncertainty the \(2\sigma\) particle image diameter uncertainty yields a value of 0.15 m/s of each measured velocity, which is around 10% relative to \(\Omega R_{\mathrm {m}}\) and about 100% relative to the maximum \(|{\overline{w}}|\) value in the groove area. Consequently, more than 100 individual velocity measurements are required to reach an uncertainty of \(\sigma _{{\overline{w}}}<\)1% relative to \(\Omega R_{\mathrm {m}}\) for the averaged velocity \({\overline{w}}\) at a certain location.
The issue of peak-locking needs to be suppressed to avoid bias errors of the measured velocities and its derivatives, as outlined by Prasad et al. (1992) and Raffel et al. (2018). Figure 9 shows the sub-pixel distribution of the particle image diameters d as well as the displacement \(\Delta X\) in sensor X direction. Both diagrams demonstrate that either diameter determination method does not lead to any peak-locking issues. Note however that peak-locking normally appears if the particle images are small and/or strong intensity gradients are present. In this imaging set-up, the particle image intensity distribution is not particularly steep at the edge (cp. Fig. 8a), as compared to the set-up with a much lower magnification used by Fuchs et al. (2016a).
To conclude this comparative analysis, it can be stated that both evaluation strategies lead to unbiased accurate results with slightly different diameter estimates for the given particle image. This difference leads to accordingly different transfer functions between image diameter and location in the measurement volume. However, these slope differences are compensated by means of the in situ calibration procedure with the well-known boundary conditions, such that both approaches yield to quantitative velocity fields in the clutch gap.
The edge detection is found to be more robust in terms of decreasing SNR, leading to a higher particle detection rate for large particle images. Therefore, the remainder of the present work will entirely build upon the edge detection results to analyze the observed flow phenomena in detail. In those cases where the diameter estimate itself is the desired information, however, the Hough-based circle detection algorithm is recommended.
Overview of the recorded flow fields: Contours of radially averaged components of normalized circumferential, radial and axial velocity (\(u_\varphi\), \(u_r\) and \(u_z\)) are shown for FOV I (\(M=7.0\)) on the left and FOV II (\(M=4.2\)) on the right. White contour color is chosen for \(u_\varphi =\Omega R_\text {m}\), \(u_r=0\) and \(u_z=0\)
3.2 Clutch flow topology
Figure 10 provides an overview of the flow situation in the clutch gap; furthermore, it illustrates the distance between the two FOV positions in circumferential direction, where the left part shows FOV I (\(M=7.0\)) representing the smooth, ungrooved gap region. The right side of the figure features the velocity information for FOV II (\(M=4.2\) and \(M=7.0\)), i.e. the flow in the grooved region of the gap and in particular within the gap. The contours denote the radially averaged values of the normalized circumferential, radial, and axial velocities (\(u_\varphi\), \(u_r\), and \(u_z\)) in the \(\varphi -z\) plane; it is expected to see the main topological flow patterns in this particular plane. Note that the white contour color corresponds to a zero contribution in the case of \(u_r\) and \(u_z\), such that changes in the flow direction are indicated more clearly. For the circumferential direction the white contour color denotes the angular disk speed \(\Omega R_\text {m}\), to better visualize how the flow velocity exceeds the angular speed within the groove.
First, the flow in the ungrooved gap region is analyzed in more detail. In accordance with Lance and Rogers (1962), the flow in that area can be considered Couette-like, since the velocity profile is close to being linear, as already discussed earlier and being indicated in Fig. 11. The radial velocity \(u_{r}\) in this gap part is completely negative—i.e. it is facing towards the clutch center—with a value that is two orders of magnitude lower than the rotational speed. In z direction, the velocity can be considered to be zero. Altogether, the velocity profiles seem to indicate that the groove influence decays quickly, since the measurement location lies only 5 grooves widths downstream of the groove. Neupert et al. (2018) consider this to be a valuable and important information for the clutch design process. The inward facing radial flow stands in contrast to previous studies with analytical solutions (e.g. Huang et al. 2012), where the maximum of the generally positive (outward facing) radial velocity profile was found to be close to the rotor disk, which was considered to be a result of the influence of the centrifugal forces on the Poiseuille-like velocity profile. However, it has to be noted that the latter study used a smooth rotor-stator configuration without grooves. For the present experiment without aeration, the fact of the inward facing radial velocity hints at a significant interaction between the grooves and the smooth parts of the rotor-stator gap.
Now, the more complex part of the clutch flow—in the vicinity of the grooves—is characterized in more detail. The Defocusing PTV measurement uncovers formerly unknown velocity information in the groove region allowing for a thorough flow analysis. Figure 12 provides a conceptual look at the expected flow topology in the \(\varphi -z\) plane inside and above the groove, for both the stator-fixed and rotor-fixed frames of reference. From left to right the sketch illustrates (1) the linear profile, (2) the velocity profile exceeding the rotational speed \(\Omega r\) within the groove, and (3) the emergence of a cavity roller, as a result of the overspeed. At the rotor disk surface, where the no-slip condition applies, the velocity matches the rotational speed \(\Omega r\). In the smooth gap region the velocity yields the rotational speed at \(z=h\) and in the grooves at \(z=h+H\), respectively. This flow topology concept along with the cavity roller, shown in Fig. 12, was described earlier in Leister and Kriegseis (2019).
a Detected data points in a \(\varphi -z\)-coordinate system. Groove edges and gap height are indicated with vertical and horizontal green lines, respectively; colored particles in the groove region are further converted to separate velocity profiles per color (see Fig. 14); b corresponding velocity information \(u_\varphi (z)\) for all detected particle-image pairs for FOV II \((M=4.2)\)
To fully capture the flow topology in the vicinity of the groove and in particular the interaction between the grooved and the smooth gap region, an experiment with a magnification of \(M=4.2\) was conducted, providing a broader picture of the flow as compared to the \(M=7.0\) experiments.
Two different approaches can be taken to determine the actual groove position from the recorded images. One approach is based on a proper orthogonal decomposition (POD), introduced by Mendez et al. (2017), that is originally intended as a means to remove background reflections from recordings. Applying the POD to the raw images clearly indicates the position of the groove edges, since the light reflections of the groove edges produce a distinct background pattern. Using this information, \(\varphi =0\) was defined to be situated at the left edge of the groove. Another approach for detecting the groove location is by looking at the spatial distribution of the detected particles. Figure 13a shows this spatial particle distribution; it becomes apparent that the grooves of the rotor disk, that is made from a porous material, do not feature sharp edges. In fact, they have a curvature of \(0.3\,\) mm that is sharply resolved by the estimated particle locations.
Normalized velocity profiles \(u_\varphi (z)\) in the rotor-fixed frame of reference for various normalized circumferential locations \(\varphi R_\text {m}/W\) inside the groove of the rotor \((M=4.2)\); color coding identical to Fig. 13
In addition to the particle distribution, Fig. 13b shows a plot of all measured \(u_\varphi (z)\) values in the large FOV. Independent of the measurement location, the variation of \(u_\varphi (z)\) close to the stator (\(z<0.5\)) stays rather small. Above \(z>0.5\), the velocities start to spread more, and this is due to the modification of the velocity profile within groove cavity. A closer look at the local circumferential velocity in the groove cavity is given in Fig. 14, where the color indicates the location of the velocity profile , which is provided in Fig. 13a. Along the gap width, the overspeed, which is the cause for the cavity roller, has the largest value in the groove center, exceeding the rotational speed \(\Omega r\) by up to 5%. In gap height direction, the velocity maximum is located in the center at \(z/h\approx 2\). Towards the edges of the groove cavity the velocity maxima become smaller, and from the left to right in gap width direction, the location of the maxima seem to shift from smaller z/h values to larger values. However, this observation is not quite true for the yellow profile, representing the right edge of the cavity. Furthermore, what becomes evident from the profiles in Fig. 14 is that in the groove region the flow is decelerated. Thus, the rotational speed of the rotor is reached only above \(z/h>1.2\) and not at \(z/h=1\) like in the case of a Couette-like flow.
Figure 15 enables a more comprehensive analysis of the cavity roller, showing the vector field of the circumferential and the axial velocity components in the rotor-fixed frame of reference, whereas the radial velocity component is shown as background contours. Furthermore, the \(\Gamma _1\)-criterion as introduced by Graftieaux et al. (2001) has been applied to the velocity field to extract the vortex-center location of the roller. The center of the vortical structure is identified for \(\Gamma _1 \approx 1\) at \((\varphi \Omega /W,\ z/h)=(0.33,\ 1.5)\), which is a downstream shift relative to the cavity center at \((\varphi R_{m}/W,\ z/h)=(0.5,\ 2)\). Both vortex center and \(\Gamma _1\)-isolines are added to Fig. 15 for clarity.
This finding is in accordance with a previous cavity roller topology investigation by Shankar and Deshpande (2000), where is was also found that the roller center moves in direction to the gap/cavity interface (in this study located at \(z/h=1\)) and towards the trailing edge in circumferential direction, which corresponds to \(\varphi R_{m}=0\) in this study. Thus, the roller is not limited to the cavity—i.e. above \(z/h=1\)—but it reaches into gap region inducing the above-mentioned deceleration of \(u_{\varphi }\) in the vicinity of the groove. This is a key information derived from the present quantitative experiments, since current analytical models for drag torque analyses of open wet clutches oversimplify or even neglect this impact as recently summarised by Leister et al. (2020).
Cavity roller in the rotor-fixed frame of reference. Contours of radial velocity \(u_r\) are superimposed by \(\Gamma _1\)-isolines ( ) and vectors of \(u_\varphi -\Omega R_{\mathrm {m}}\) and \(u_z\). (
) and vectors of \(u_\varphi -\Omega R_{\mathrm {m}}\) and \(u_z\). ( )
indicates the \(\Gamma _1\) vortex-center location. A separatrix (
)
indicates the \(\Gamma _1\) vortex-center location. A separatrix ( ) originated at the backward facing edge is added to indicate the separation of the gap- and cavity-flow domains \((M=4.2)\)
) originated at the backward facing edge is added to indicate the separation of the gap- and cavity-flow domains \((M=4.2)\)
Looking at Fig. 10 again, the interaction between the inward facing flow, with distance to the groove, and outward facing flow, in the groove vicinity, can be analysed in more detail. The magnitude of the radial flow reaches at maximum 5% of the disk speed \(\Omega R_\mathrm {m}\). The clear separation of the volumetric flow rate Q into a negative radial flux in the groove and a positive flux within the groove does not hold true. Instead, the positive radial flow spreads out from the groove into the gap, reaching further downstream from the forward facing cavity edge.
A quantification of the spatial extent of this gap flow modification is given in Fig. 15 in terms of a so-called separatrix (see e.g. Perry and Chong 1987; Foss 2004, for more details on flow topology). This separatrix is drawn from the half-saddle of the backwards facing edge. Obviously, the separatrix does not enclose the fluid inside the cavity but rather drifts into the gap in a flow region of positive radial velocity as an effect of the displacement by the roller.
As mentioned before, the volume flow rate Q was adjusted such that no air entered the gap. Despite the absence of aeration, the appearance flow reversals are a new observation, since the aeration onset is commonly assumed to occur before flow reversals as outlined e.g. by Huang et al. (2012). Thus, it is of utmost importance to thoroughly examine the wall shear foot print of the observed flow patterns on the stator disk in so as to provide an appropriate estimate of the effect on the overall drag torque of the clutch.
3.3 Wall shear stress at stator
Comparison of measured velocity profiles from different circumferential locations with the ideal linear profile ( ). Ungrooved region of FOV I at \(\varphi R_\text {m}/W=-4.97\pm 0.11\) (
). Ungrooved region of FOV I at \(\varphi R_\text {m}/W=-4.97\pm 0.11\) ( ); ungrooved region of FOV II immediately next to the groove at \(\varphi R_\text {m}/W=1.47\pm 0.11\) (
); ungrooved region of FOV II immediately next to the groove at \(\varphi R_\text {m}/W=1.47\pm 0.11\) ( ); center part of the groove (FOV II) at \(\varphi R_\text {m}/W=0.67\pm 0.11\) (
); center part of the groove (FOV II) at \(\varphi R_\text {m}/W=0.67\pm 0.11\) ( ). The insert emphasizes the different slopes of \(u_\varphi (h)\) in vicinity above the stator plate and indicates the linear approximation for the WSS estimate (\(M=7\))
). The insert emphasizes the different slopes of \(u_\varphi (h)\) in vicinity above the stator plate and indicates the linear approximation for the WSS estimate (\(M=7\))
In general, the wall shear stress (WSS, \(\tau _{w}\)) is an essential quantity for the scaling analysis of near wall flow statistics and turbulence modeling. For technical devices such as the present open wet clutch flow, a detailed knowledge of the WSS is of particular importance, since it has significant influence on the performance of the device in terms of adverse drag torque effects. Since radial fluxes and corresponding velocity gradients \(\partial u_r/\partial z\) do not contribute to the drag torque \(T_s\), only the circumferential component \(\partial u_\varphi /\partial z\) is considered and the WSS at the stator is accordingly defined as
for the given problem.
Today’s torque models for clutch design commonly treat the WSS as a global parameter without local information to account for grooves or distributed surface structures. The direct comparison of velocity profiles at different locations along the perimeter, as shown in Fig. 16, indicates that this global estimate in fact is an oversimplification of the flow scenario under the presence of grooves, since all curves deviate at least slightly (yet significantly) from the ideal linear profile. In fact, the curvature \(u_\varphi\) changes from \(\partial ^2u_\varphi /\partial z^2>0\) measured in FOV I midway between the grooves ( : \(\varphi R_\text {m}/W=-4.97\pm 0.11\)), to \(\partial ^2u_\varphi /\partial z^2<0\) in the vicinity of the groove in FOV II (
: \(\varphi R_\text {m}/W=-4.97\pm 0.11\)), to \(\partial ^2u_\varphi /\partial z^2<0\) in the vicinity of the groove in FOV II ( : measured directly before the groove; measured in the groove center,
: measured directly before the groove; measured in the groove center,  : \(\varphi R_\text {m}/W=0.67\pm 0.11\)). As a consequence, there has to be a variation in the local WSS. In this WSS estimation approach, \(\tau _{\mathrm {w}}\) is determined by a linear fit of \(u_{\varphi }(z)\) in proximity of the stator (\(z/h<0.1\)). The estimated values are normalized with the ideal WSS \(\tau _{\mathrm {w,lin}}=\Omega r/h\) of an ideal linear Couette profile. Note that \(\tau _{\mathrm {w,lin}}\) increases with increasing radial position r of the measurement.
: \(\varphi R_\text {m}/W=0.67\pm 0.11\)). As a consequence, there has to be a variation in the local WSS. In this WSS estimation approach, \(\tau _{\mathrm {w}}\) is determined by a linear fit of \(u_{\varphi }(z)\) in proximity of the stator (\(z/h<0.1\)). The estimated values are normalized with the ideal WSS \(\tau _{\mathrm {w,lin}}=\Omega r/h\) of an ideal linear Couette profile. Note that \(\tau _{\mathrm {w,lin}}\) increases with increasing radial position r of the measurement.
The wall shear stress (WSS) increases by up to \(15\;\%\) in the vicinity of the groove (red line, FOV II), as compared to the WSS of an ideal linear profile. Unlike that, the WSS in the ungrooved gap area, represented by FOV I (green line), lies around \(4\;\%\) below that of the ideal linear reference (\(M=7\))
The local values of the normalized WSS, calculated as
are shown in a combined diagram in Fig. 17. For FOV I, values in radial direction are plotted ( ), and for FOV II across the groove in the circumferential direction (
), and for FOV II across the groove in the circumferential direction ( ). The WSS values are found to be around 4% below the reference value of the linear profile for the smooth gap flow between the grooves (FOV I). Assuming a constant normalized WSS \(\tau _\text {w}^*\) in radial direction, the measured values can be used to calculate the uncertainty of the WSS estimation, yielding \(2\sigma =1.01\)%. However, it has to be emphasized that this uncertainty measure can only provide the order of magnitude of the uncertainty. A reference experiment with a well-known WSS distribution is required for a precise quantification of the uncertainty.
). The WSS values are found to be around 4% below the reference value of the linear profile for the smooth gap flow between the grooves (FOV I). Assuming a constant normalized WSS \(\tau _\text {w}^*\) in radial direction, the measured values can be used to calculate the uncertainty of the WSS estimation, yielding \(2\sigma =1.01\)%. However, it has to be emphasized that this uncertainty measure can only provide the order of magnitude of the uncertainty. A reference experiment with a well-known WSS distribution is required for a precise quantification of the uncertainty.
In contrast to FOV I, the circumferential WSS distribution along \(\varphi R_\text {m}/W\) reveals a range of WSS values from 9% to 15% above the reference of \(\tau _\text {w}^*=1\). This increase reflects the flow profile modification due to the cavity roller, which extends considerably into the gap and, therefore, slightly displaces the faster fluid towards the stator wall (recall the separatrix of Fig. 15). Together with the identification of the cavity roller, the determination of the local drag torque is the most important result of this study, since it serves as a first step into a better understanding of the interaction between the grooves and the resulting drag torque.
4 Conclusions
Particle imaging for industrial applications is often challenging, in particular if the flow of interest has limited optical access and requires a volumetric analysis. The in situ calibrated DPTV approach as used in the present study has proven to be a robust and reliable 3D3C velocimetry technique with only one camera, which allows for a comprehensive analysis of the flow in an open wet clutch.
The diameter of the recorded particle images were determined with an edge detection algorithm and a Hough-transform approach that both were compared in terms of different performance measures. Both strategies revealed no signs of peak-locking and an uncertainty assessment confirmed that the accuracy of a previous, generic lab experiment can be met, yielding a spatial resolution of around 12.5 \(\upmu \mathrm{m}\) for the in-plane velocities along the optical axis. Such a high resolution turned out to be essential to discover the complex flow structures that are associated with technical applications like in this grooved open wet clutch, which can be described as complex, wall-bounded, sub-millimetre shear flow problem. Since to date no rigorous analysis of the velocity in open wet clutches was done to enlighten the cause-effect relations of aeration, the present Defocusing PTV investigation for the case of a radially grooved clutch-disk geometry uncovers several insightful flow patterns.
The results demonstrate that the velocity of the shear flow in circumferential direction follows a Couette-like profile in a sufficiently large distance from the grooves. The intra-groove analysis uncovers a formerly hidden vortical structure, which is similar to a cavity roller.
A further topological analysis of the roller demonstrated that the vortex extends into the gap and consequently displaces the gap flow. Moreover, a characteristic separatrix indicates that considerable amounts of fluid are fed into the gap from the groove. An evaluation of the underlying radial fluxes clearly shows that the majority of the volumetric flow rate passes the clutch through the grooves in positive radial direction. These positive fluxes are also convected into the gap downstream of the groove due to the above-mentioned feeding process. This process is not considered in the current drag torque prediction models that are currently being used by the clutch manufacturers. Simultaneously, midway between the grooves, a reverse flow in radial direction is present. This reverse flow is arguably being fed from the outward facing radial flow in the groove at larger radii, as there is no air in the gap. However, the inhomogeneity of radial fluxes across the circumference can be the cause why previous studies found an earlier start of aeration using grooved rotor disks, as compared to smooth rotor disks.
For the design and modelling process of an open wet clutch, the wall shear stress is a decisive quantity. Here, the Defocusing PTV approach reveals that the local wall shear stress changes significantly. Midway between the grooves the curvature of the velocity profile was found to be positive, yielding a wall shear stress that lies approximately 4% lower compared to the reference value of the ideal linear profile. Unlike this, in the vicinity of the groove, the wall shear stress increases to up to 15% above the stress value of an ideal linear velocity profile. Thus, it can be concluded that a detailed knowledge of the interaction between the topology of the cavity roller and the resulting modification of the velocity profile, which is equivalent to a modification of the shear stresses at the opposite disk, is of utmost importance for future, efficiency enhanced groove designs.
Finally, the insights and conclusions of this study clearly underline the value of particle imaging techniques for velocity measurements in industrial applications and might, moreover, contribute towards a deeper understanding of cause-effect relations between the various groove geometries and their respective flow topologies and the resulting drag torque of open wet clutches.
References
Barnkob R, Kähler CJ, Rossi M (2015) General defocusing particle tracking. Lab Chip 15(17):3556–3560. https://doi.org/10.1039/C5LC00562K
Cierpka C, Segura R, Hain R, Kähler CJ (2010) A simple single camera 3c3d velocity measurement technique without errors due to depth of correlation and spatial averaging for microfluidics. Measur Sci Technol 21(4):045401. https://doi.org/10.1088/0957-0233/21/4/045401
Elsinga G, Scarano F, Wieneke B, van Oudheusden B (2006) Double-frame 3d-ptv using a tomographic predictor. Exp Fluids 41(6):933–947. https://doi.org/10.1007/s00348-006-0212-z
Foss JF (2004) Surface selections and topological constraint evaluations for flow field analyses. Exp Fluids 37:883–898. https://doi.org/10.1007/s00348-004-0877-0
Fuchs T, Hain R, Kähler CJ (2014) Three-dimensional location of micrometer-sized particles in macroscopic domains using astigmatic aberrations. Opt Lett 39(5):1298–1301. https://doi.org/10.1364/OL.39.001298
Fuchs T, Hain R, Kähler CJ (2016a) In situ calibrated defocusing ptv for wall-bounded measurement volumes. Measur Sci Technol 27(8):084005. https://doi.org/10.1088/0957-0233/27/8/084005
Fuchs T, Hain R, Kähler CJ (2016b) Uncertainty quantification of three-dimensional velocimetry techniques for small measurement depths. Exp Fluids 57(5):73. https://doi.org/10.1007/s00348-016-2161-5
Graftieaux L, Michard M, Grosjean N (2001) Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Measure Sci Technol 12:1422–1429. https://doi.org/10.1088/0957-0233/12/9/307
Gropper D, Wang L, Harvey TJ (2016) Hydrodynamic lubrication of textured surfaces: a review of modeling techniques and key findings. Tribol Int 94:509–529. https://doi.org/10.1016/j.triboint.2015.10.009
Hough PVC (1959) Machine Analysis of Bubble Chamber Pictures. In: Proceedings, 2nd international conference on high-energy accelerators and instrumentation C590914:554–558. https://s3.cern.ch/inspire-prod-files-5/53d80b0393096ba4afe34f5b65152090
Huang J, Wei J, Qiu M (2012) Laminar flow in the gap between two rotating parallel frictional plates in hydro-viscous drive. Chin J Mech Eng 25(1):144–152. https://doi.org/10.3901/CJME.2012.01.144
Iqbal S, Al-Bender F, Pluymers B, Desmet W (2013a) Experimental characterization of drag torque in open multi-disks wet clutches. SAE Int J Fuels Lubricants 6(3):894–906. http://www.jstor.org/stable/26273281
Iqbal S, Al-Bender F, Pluymers B, Desmet W (2013b) Mathematical model and experimental evaluation of drag torque in disengaged wet clutches. ISRN Tribol 2013:1–16. https://doi.org/10.5402/2013/206539
Kriegseis J, Mattern P, Dues M (2016) Combined planar piv and lda profile-sensor measurements in a rotor-stator disk configuration. In: 18th International symposium on the application of laser and imaging techniques to fluid mechanics, Lisbon, Portugal, July 4-7. https://ila-rnd.com/wp-content/uploads/2019/05/Lit_LDV_PS_LISBON2016_Kriegseis_V4.pdf
Lance GN, Rogers MH (1962) The axially symmetric flow of a viscous fluid between two infinite rotating disk. Proc R Soc Lond Ser A Math Phys Sci 266(1324):109–121. http://www.jstor.org/stable/2414223
Leister R, Kriegseis J (2019) 3D-LIF experiments in an open wet clutch by means of defocusing PTV. In: Kähler CJ, Hain R, Scharnowski S, Fuchs T (eds) Proceedings of the 13th international symposium on particle image velocimetry, https://athene-forschung.unibw.de/doc/129141/129141.pdf
Leister R, Najafi AF, Gatti D, Kriegseis J, Frohnapfel B (2020) Non-dimensional characteristics of open wet clutches for advanced drag torque and aeration predictions. Tribol Int. https://doi.org/10.1016/j.triboint.2020.106442
Mendez M, Raiola M, Masullo A, Discetti S, Ianiro A, Theunissen R, Buchlin JM (2017) Pod-based background removal for particle image velocimetry. Exp Thermal Fluid Sci 80:181–192. https://doi.org/10.1016/j.expthermflusci.2016.08.021
Neupert T, Bartel D (2019) High-resolution 3d cfd multiphase simulation of the flow and the drag torque of wet clutch discs considering free surfaces. Tribol Int 129:283–296. https://doi.org/10.1016/j.triboint.2018.08.031
Neupert T, Benke E, Bartel D (2018) Parameter study on the influence of a radial groove design on the drag torque of wet clutch discs in comparison with analytical models. Tribol Int 119:809–821. https://doi.org/10.1016/j.triboint.2017.12.005
Nishino N, Kasagi N, Hirata M (1989) Three-dimensional particle tracking velocimetry based on automated digital image processing. J Fluids Eng 111(4):384–391. https://doi.org/10.1115/1.3243657
Olsen MG, Adrian RJ (2000) Out-of-focus effects on particle image visibility and correlation in microscopic particle image velocimetry. Exp Fluids 29(7):S166–S174. https://doi.org/10.1007/s003480070018
Pahlovy SA, Mahmud SF, Kubota M, Ogawa M, Takakura N (2016) Prediction of drag torque in a disengaged wet clutch of automatic transmission by analytical modeling. Tribol Online 11(2):121–129. https://doi.org/10.2474/trol.11.121
Perry AE, Chong MS (1987) A description of eddying motions and flow patterns using critical-point concepts. Annu Rev Fluid Mech 19:125–155. https://doi.org/10.1146/annurev.fl.19.010187.001013
Prasad AK, Adrian RJ, Landreth CC, Offutt PW (1992) Effect of resolution on the speed and accuracy of particle image velocimetry interrogation. Exp Fluids 13:105–116. https://doi.org/10.1007/BF00218156
Raffel M, Willert CE, Scarano F, Kähler CJ, Wereley ST (2018) Particle image velocimetry. Springer, New York. https://doi.org/10.1007/978-3-319-68852-7
Shankar PN, Deshpande MD (2000) Fluid mechanics in the driven cavity. Annu Rev Fluid Mech 32(1):93–136. https://doi.org/10.1146/annurev.fluid.32.1.93
Takagi Y, Okano Y, Miyayaga M, Katayama N (2012) Numerical and physical experiments on drag torque in a wet clutch. Tribol Online 7(4):242–248. https://doi.org/10.2474/trol.7.242
Tauviqirrahman M, Ismail R, Jamari J, Schipper DJ (2013) A study of surface texturing and boundary slip on improving the load support of lubricated parallel sliding contacts. Acta Mech 224:365–381. https://doi.org/10.1007/s00707-012-0752-7
Willert CE, Gharib M (1992) Three-dimensional particle imaging with a single camera. Exp Fluids 12(6):353–358. https://doi.org/10.1007/BF00193880
Wu M, Roberts JW, Buckley M (2005) Three-dimensional fluorescent particle tracking at micron-scale using a single camera. Exp Fluids 38(4):461–465. https://doi.org/10.1007/s00348-004-0925-9
Yuan S, Guo K, Hu J, Peng Z (2010) Study on aeration for disengaged wet clutches using a two-phase flow model. J Fluids Eng. https://doi.org/10.1115/1.4002874
Acknowledgements
The authors gratefully acknowledge technical support with the clutch model from IPEK at KIT and the loan of a Questar long-distance microscope from SLA at TU Darmstadt. Thanks Johannes for the immediate courier service!
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Leister, R., Fuchs, T., Mattern, P. et al. Flow-structure identification in a radially grooved open wet clutch by means of defocusing particle tracking velocimetry. Exp Fluids 62, 29 (2021). https://doi.org/10.1007/s00348-020-03116-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00348-020-03116-0


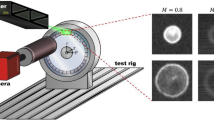









 and edge
and edge  detection approaches (M = 7)
detection approaches (M = 7)
 ) and edge (
) and edge ( ) detection approaches (
) detection approaches (






